- Book a Demo

17 Smart Problem-Solving Strategies: Master Complex Problems
- March 3, 2024
- Productivity
- 25 min read

Struggling to overcome challenges in your life? We all face problems, big and small, on a regular basis.
So how do you tackle them effectively? What are some key problem-solving strategies and skills that can guide you?
Effective problem-solving requires breaking issues down logically, generating solutions creatively, weighing choices critically, and adapting plans flexibly based on outcomes. Useful strategies range from leveraging past solutions that have worked to visualizing problems through diagrams. Core skills include analytical abilities, innovative thinking, and collaboration.
Want to improve your problem-solving skills? Keep reading to find out 17 effective problem-solving strategies, key skills, common obstacles to watch for, and tips on improving your overall problem-solving skills.
Key Takeaways:
- Effective problem-solving requires breaking down issues logically, generating multiple solutions creatively, weighing choices critically, and adapting plans based on outcomes.
- Useful problem-solving strategies range from leveraging past solutions to brainstorming with groups to visualizing problems through diagrams and models.
- Core skills include analytical abilities, innovative thinking, decision-making, and team collaboration to solve problems.
- Common obstacles include fear of failure, information gaps, fixed mindsets, confirmation bias, and groupthink.
- Boosting problem-solving skills involves learning from experts, actively practicing, soliciting feedback, and analyzing others’ success.
- Onethread’s project management capabilities align with effective problem-solving tenets – facilitating structured solutions, tracking progress, and capturing lessons learned.
What Is Problem-Solving?
Problem-solving is the process of understanding an issue, situation, or challenge that needs to be addressed and then systematically working through possible solutions to arrive at the best outcome.
It involves critical thinking, analysis, logic, creativity, research, planning, reflection, and patience in order to overcome obstacles and find effective answers to complex questions or problems.
The ultimate goal is to implement the chosen solution successfully.
What Are Problem-Solving Strategies?
Problem-solving strategies are like frameworks or methodologies that help us solve tricky puzzles or problems we face in the workplace, at home, or with friends.
Imagine you have a big jigsaw puzzle. One strategy might be to start with the corner pieces. Another could be looking for pieces with the same colors.
Just like in puzzles, in real life, we use different plans or steps to find solutions to problems. These strategies help us think clearly, make good choices, and find the best answers without getting too stressed or giving up.
Why Is It Important To Know Different Problem-Solving Strategies?
Knowing different problem-solving strategies is important because different types of problems often require different approaches to solve them effectively. Having a variety of strategies to choose from allows you to select the best method for the specific problem you are trying to solve.
This improves your ability to analyze issues thoroughly, develop solutions creatively, and tackle problems from multiple angles. Knowing multiple strategies also aids in overcoming roadblocks if your initial approach is not working.
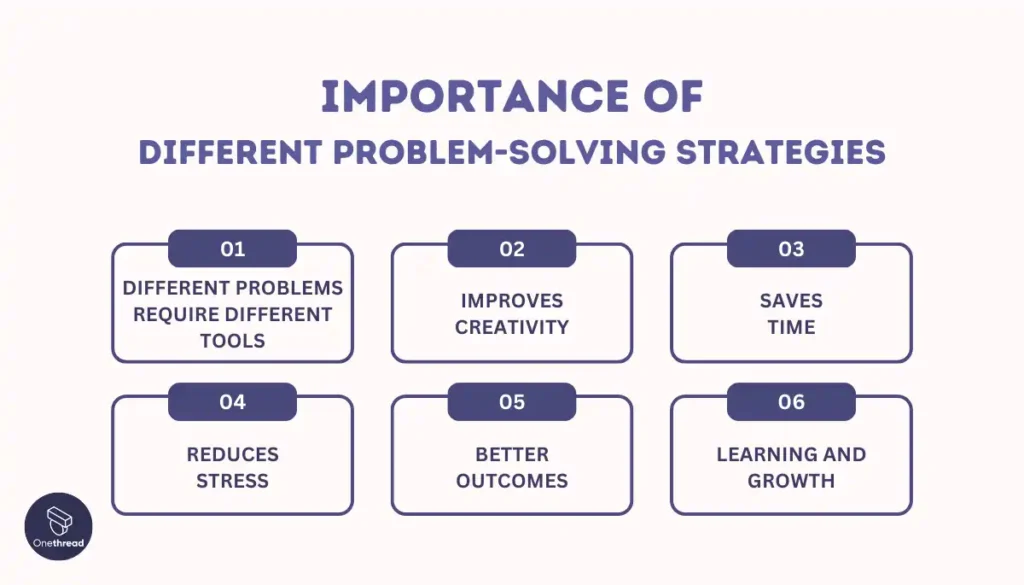
Here are some reasons why you need to know different problem-solving strategies:
- Different Problems Require Different Tools: Just like you can’t use a hammer to fix everything, some problems need specific strategies to solve them.
- Improves Creativity: Knowing various strategies helps you think outside the box and come up with creative solutions.
- Saves Time: With the right strategy, you can solve problems faster instead of trying things that don’t work.
- Reduces Stress: When you know how to tackle a problem, it feels less scary and you feel more confident.
- Better Outcomes: Using the right strategy can lead to better solutions, making things work out better in the end.
- Learning and Growth: Each time you solve a problem, you learn something new, which makes you smarter and better at solving future problems.
Knowing different ways to solve problems helps you tackle anything that comes your way, making life a bit easier and more fun!
17 Effective Problem-Solving Strategies
Effective problem-solving strategies include breaking the problem into smaller parts, brainstorming multiple solutions, evaluating the pros and cons of each, and choosing the most viable option.
Critical thinking and creativity are essential in developing innovative solutions. Collaboration with others can also provide diverse perspectives and ideas.
By applying these strategies, you can tackle complex issues more effectively.
Now, consider a challenge you’re dealing with. Which strategy could help you find a solution? Here we will discuss key problem strategies in detail.
1. Use a Past Solution That Worked

This strategy involves looking back at previous similar problems you have faced and the solutions that were effective in solving them.
It is useful when you are facing a problem that is very similar to something you have already solved. The main benefit is that you don’t have to come up with a brand new solution – you already know the method that worked before will likely work again.
However, the limitation is that the current problem may have some unique aspects or differences that mean your old solution is not fully applicable.
The ideal process is to thoroughly analyze the new challenge, identify the key similarities and differences versus the past case, adapt the old solution as needed to align with the current context, and then pilot it carefully before full implementation.
An example is using the same negotiation tactics from purchasing your previous home when putting in an offer on a new house. Key terms would be adjusted but overall it can save significant time versus developing a brand new strategy.
2. Brainstorm Solutions

This involves gathering a group of people together to generate as many potential solutions to a problem as possible.
It is effective when you need creative ideas to solve a complex or challenging issue. By getting input from multiple people with diverse perspectives, you increase the likelihood of finding an innovative solution.
The main limitation is that brainstorming sessions can sometimes turn into unproductive gripe sessions or discussions rather than focusing on productive ideation —so they need to be properly facilitated.
The key to an effective brainstorming session is setting some basic ground rules upfront and having an experienced facilitator guide the discussion. Rules often include encouraging wild ideas, avoiding criticism of ideas during the ideation phase, and building on others’ ideas.
For instance, a struggling startup might hold a session where ideas for turnaround plans are generated and then formalized with financials and metrics.
3. Work Backward from the Solution

This technique involves envisioning that the problem has already been solved and then working step-by-step backward toward the current state.
This strategy is particularly helpful for long-term, multi-step problems. By starting from the imagined solution and identifying all the steps required to reach it, you can systematically determine the actions needed. It lets you tackle a big hairy problem through smaller, reversible steps.
A limitation is that this approach may not be possible if you cannot accurately envision the solution state to start with.
The approach helps drive logical systematic thinking for complex problem-solving, but should still be combined with creative brainstorming of alternative scenarios and solutions.
An example is planning for an event – you would imagine the successful event occurring, then determine the tasks needed the week before, two weeks before, etc. all the way back to the present.
4. Use the Kipling Method
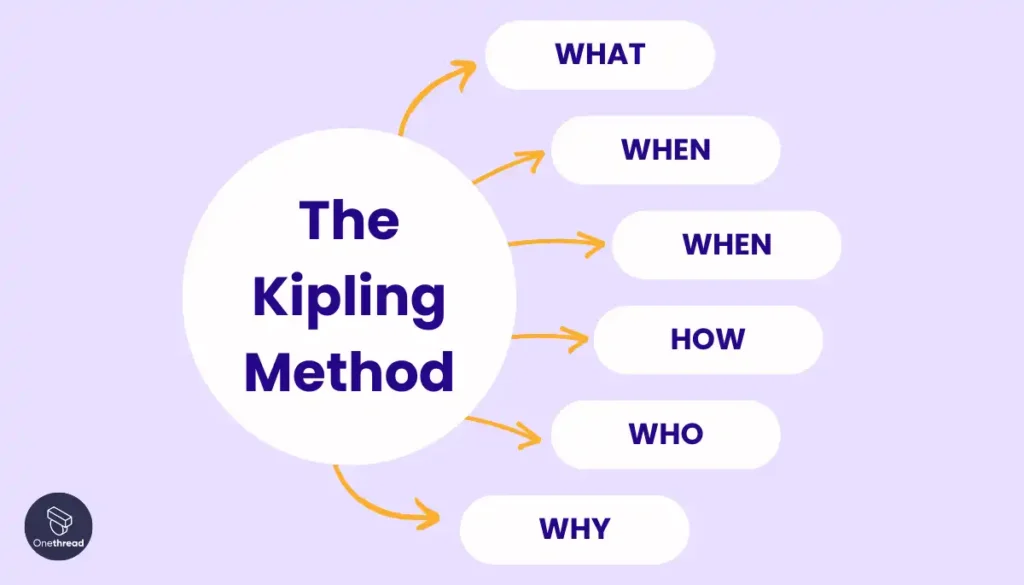
This method, named after author Rudyard Kipling, provides a framework for thoroughly analyzing a problem before jumping into solutions.
It consists of answering six fundamental questions: What, Where, When, How, Who, and Why about the challenge. Clearly defining these core elements of the problem sets the stage for generating targeted solutions.
The Kipling method enables a deep understanding of problem parameters and root causes before solution identification. By jumping to brainstorm solutions too early, critical information can be missed or the problem is loosely defined, reducing solution quality.
Answering the six fundamental questions illuminates all angles of the issue. This takes time but pays dividends in generating optimal solutions later tuned precisely to the true underlying problem.
The limitation is that meticulously working through numerous questions before addressing solutions can slow progress.
The best approach blends structured problem decomposition techniques like the Kipling method with spurring innovative solution ideation from a diverse team.
An example is using this technique after a technical process failure – the team would systematically detail What failed, Where/When did it fail, How it failed (sequence of events), Who was involved, and Why it likely failed before exploring preventative solutions.
5. Try Different Solutions Until One Works (Trial and Error)

This technique involves attempting various potential solutions sequentially until finding one that successfully solves the problem.
Trial and error works best when facing a concrete, bounded challenge with clear solution criteria and a small number of discrete options to try. By methodically testing solutions, you can determine the faulty component.
A limitation is that it can be time-intensive if the working solution set is large.
The key is limiting the variable set first. For technical problems, this boundary is inherent and each element can be iteratively tested. But for business issues, artificial constraints may be required – setting decision rules upfront to reduce options before testing.
Furthermore, hypothesis-driven experimentation is far superior to blind trial and error – have logic for why Option A may outperform Option B.
Examples include fixing printer jams by testing different paper tray and cable configurations or resolving website errors by tweaking CSS/HTML line-by-line until the code functions properly.
6. Use Proven Formulas or Frameworks (Heuristics)
Heuristics refers to applying existing problem-solving formulas or frameworks rather than addressing issues completely from scratch.
This allows leveraging established best practices rather than reinventing the wheel each time.
It is effective when facing recurrent, common challenges where proven structured approaches exist.
However, heuristics may force-fit solutions to non-standard problems.
For example, a cost-benefit analysis can be used instead of custom weighting schemes to analyze potential process improvements.
Onethread allows teams to define, save, and replicate configurable project templates so proven workflows can be reliably applied across problems with some consistency rather than fully custom one-off approaches each time.
Try One thread
Experience One thread full potential, with all its features unlocked. Sign up now to start your 14-day free trial!
7. Trust Your Instincts (Insight Problem-Solving)

Insight is a problem-solving technique that involves waiting patiently for an unexpected “aha moment” when the solution pops into your mind.
It works well for personal challenges that require intuitive realizations over calculated logic. The unconscious mind makes connections leading to flashes of insight when relaxing or doing mundane tasks unrelated to the actual problem.
Benefits include out-of-the-box creative solutions. However, the limitations are that insights can’t be forced and may never come at all if too complex. Critical analysis is still required after initial insights.
A real-life example would be a writer struggling with how to end a novel. Despite extensive brainstorming, they feel stuck. Eventually while gardening one day, a perfect unexpected plot twist sparks an ideal conclusion. However, once written they still carefully review if the ending flows logically from the rest of the story.
8. Reverse Engineer the Problem

This approach involves deconstructing a problem in reverse sequential order from the current undesirable outcome back to the initial root causes.
By mapping the chain of events backward, you can identify the origin of where things went wrong and establish the critical junctures for solving it moving ahead. Reverse engineering provides diagnostic clarity on multi-step problems.
However, the limitation is that it focuses heavily on autopsying the past versus innovating improved future solutions.
An example is tracing back from a server outage, through the cascade of infrastructure failures that led to it finally terminating at the initial script error that triggered the crisis. This root cause would then inform the preventative measure.
9. Break Down Obstacles Between Current and Goal State (Means-End Analysis)

This technique defines the current problem state and the desired end goal state, then systematically identifies obstacles in the way of getting from one to the other.
By mapping the barriers or gaps, you can then develop solutions to address each one. This methodically connects the problem to solutions.
A limitation is that some obstacles may be unknown upfront and only emerge later.
For example, you can list down all the steps required for a new product launch – current state through production, marketing, sales, distribution, etc. to full launch (goal state) – to highlight where resource constraints or other blocks exist so they can be addressed.
Onethread allows dividing big-picture projects into discrete, manageable phases, milestones, and tasks to simplify execution just as problems can be decomposed into more achievable components. Features like dependency mapping further reinforce interconnections.
Using Onethread’s issues and subtasks feature, messy problems can be decomposed into manageable chunks.
10. Ask “Why” Five Times to Identify the Root Cause (The 5 Whys)

This technique involves asking “Why did this problem occur?” and then responding with an answer that is again met with asking “Why?” This process repeats five times until the root cause is revealed.
Continually asking why digs deeper from surface symptoms to underlying systemic issues.
It is effective for getting to the source of problems originating from human error or process breakdowns.
However, some complex issues may have multiple tangled root causes not solvable through this approach alone.
An example is a retail store experiencing a sudden decline in customers. Successively asking why five times may trace an initial drop to parking challenges, stemming from a city construction project – the true starting point to address.
11. Evaluate Strengths, Weaknesses, Opportunities, and Threats (SWOT Analysis)

This involves analyzing a problem or proposed solution by categorizing internal and external factors into a 2×2 matrix: Strengths, Weaknesses as the internal rows; Opportunities and Threats as the external columns.
Systematically identifying these elements provides balanced insight to evaluate options and risks. It is impactful when evaluating alternative solutions or developing strategy amid complexity or uncertainty.
The key benefit of SWOT analysis is enabling multi-dimensional thinking when rationally evaluating options. Rather than getting anchored on just the upsides or the existing way of operating, it urges a systematic assessment through four different lenses:
- Internal Strengths: Our core competencies/advantages able to deliver success
- Internal Weaknesses: Gaps/vulnerabilities we need to manage
- External Opportunities: Ways we can differentiate/drive additional value
- External Threats: Risks we must navigate or mitigate
Multiperspective analysis provides the needed holistic view of the balanced risk vs. reward equation for strategic decision making amid uncertainty.
However, SWOT can feel restrictive if not tailored and evolved for different issue types.
Teams should view SWOT analysis as a starting point, augmenting it further for distinct scenarios.
An example is performing a SWOT analysis on whether a small business should expand into a new market – evaluating internal capabilities to execute vs. risks in the external competitive and demand environment to inform the growth decision with eyes wide open.
12. Compare Current vs Expected Performance (Gap Analysis)

This technique involves comparing the current state of performance, output, or results to the desired or expected levels to highlight shortfalls.
By quantifying the gaps, you can identify problem areas and prioritize address solutions.
Gap analysis is based on the simple principle – “you can’t improve what you don’t measure.” It enables facts-driven problem diagnosis by highlighting delta to goals, not just vague dissatisfaction that something seems wrong. And measurement immediately suggests improvement opportunities – address the biggest gaps first.
This data orientation also supports ROI analysis on fixing issues – the return from closing larger gaps outweighs narrowly targeting smaller performance deficiencies.
However, the approach is only effective if robust standards and metrics exist as the benchmark to evaluate against. Organizations should invest upfront in establishing performance frameworks.
Furthermore, while numbers are invaluable, the human context behind problems should not be ignored – quantitative versus qualitative gap assessment is optimally blended.
For example, if usage declines are noted during software gap analysis, this could be used as a signal to improve user experience through design.
13. Observe Processes from the Frontline (Gemba Walk)
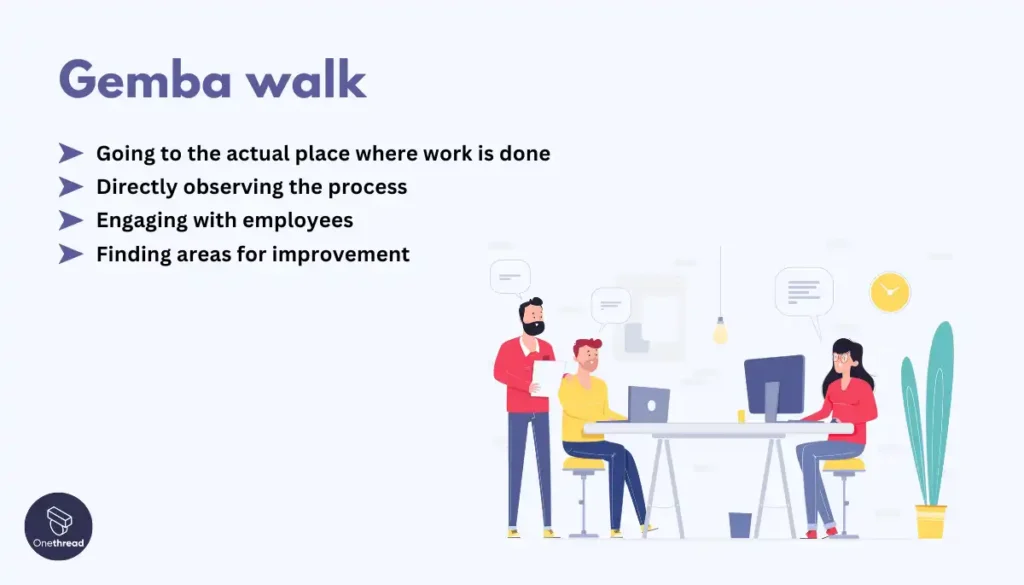
A Gemba walk involves going to the actual place where work is done, directly observing the process, engaging with employees, and finding areas for improvement.
By experiencing firsthand rather than solely reviewing abstract reports, practical problems and ideas emerge.
The limitation is Gemba walks provide anecdotes not statistically significant data. It complements but does not replace comprehensive performance measurement.
An example is a factory manager inspecting the production line to spot jam areas based on direct reality rather than relying on throughput dashboards alone back in her office. Frontline insights prove invaluable.
14. Analyze Competitive Forces (Porter’s Five Forces)
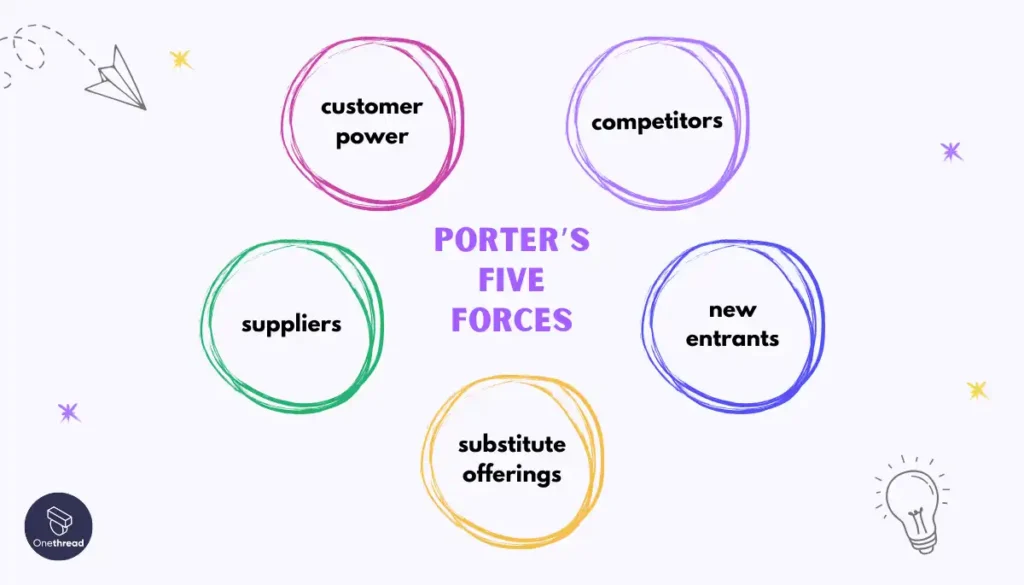
This involves assessing the marketplace around a problem or business situation via five key factors: competitors, new entrants, substitute offerings, suppliers, and customer power.
Evaluating these forces illuminates risks and opportunities for strategy development and issue resolution. It is effective for understanding dynamic external threats and opportunities when operating in a contested space.
However, over-indexing on only external factors can overlook the internal capabilities needed to execute solutions.
A startup CEO, for example, may analyze market entry barriers, whitespace opportunities, and disruption risks across these five forces to shape new product rollout strategies and marketing approaches.
15. Think from Different Perspectives (Six Thinking Hats)
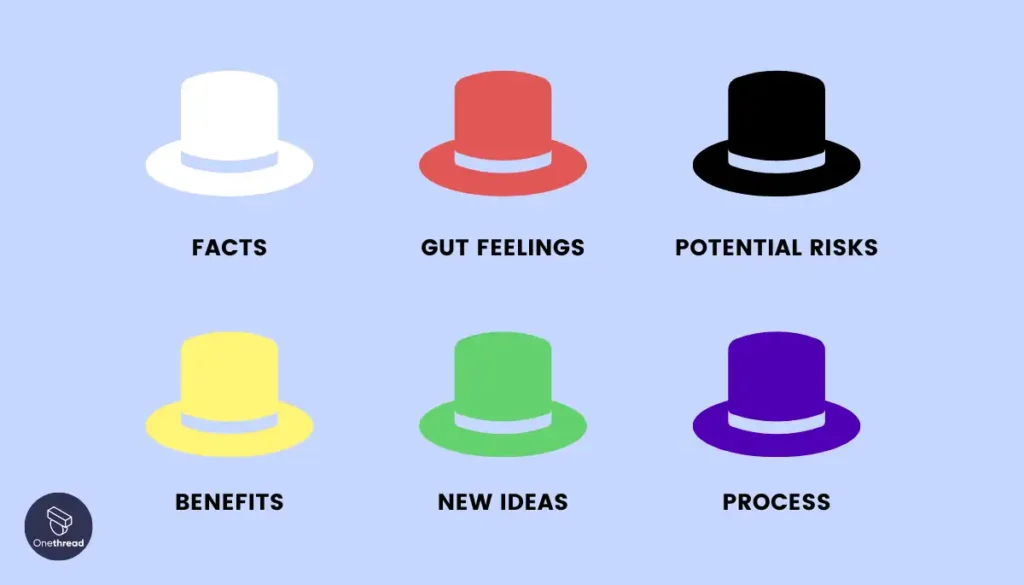
The Six Thinking Hats is a technique developed by Edward de Bono that encourages people to think about a problem from six different perspectives, each represented by a colored “thinking hat.”
The key benefit of this strategy is that it pushes team members to move outside their usual thinking style and consider new angles. This brings more diverse ideas and solutions to the table.
It works best for complex problems that require innovative solutions and when a team is stuck in an unproductive debate. The structured framework keeps the conversation flowing in a positive direction.
Limitations are that it requires training on the method itself and may feel unnatural at first. Team dynamics can also influence success – some members may dominate certain “hats” while others remain quiet.
A real-life example is a software company debating whether to build a new feature. The white hat focuses on facts, red on gut feelings, black on potential risks, yellow on benefits, green on new ideas, and blue on process. This exposes more balanced perspectives before deciding.
Onethread centralizes diverse stakeholder communication onto one platform, ensuring all voices are incorporated when evaluating project tradeoffs, just as problem-solving should consider multifaceted solutions.
16. Visualize the Problem (Draw it Out)
Drawing out a problem involves creating visual representations like diagrams, flowcharts, and maps to work through challenging issues.
This strategy is helpful when dealing with complex situations with lots of interconnected components. The visuals simplify the complexity so you can thoroughly understand the problem and all its nuances.
Key benefits are that it allows more stakeholders to get on the same page regarding root causes and it sparks new creative solutions as connections are made visually.
However, simple problems with few variables don’t require extensive diagrams. Additionally, some challenges are so multidimensional that fully capturing every aspect is difficult.
A real-life example would be mapping out all the possible causes leading to decreased client satisfaction at a law firm. An intricate fishbone diagram with branches for issues like service delivery, technology, facilities, culture, and vendor partnerships allows the team to trace problems back to their origins and brainstorm targeted fixes.
17. Follow a Step-by-Step Procedure (Algorithms)

An algorithm is a predefined step-by-step process that is guaranteed to produce the correct solution if implemented properly.
Using algorithms is effective when facing problems that have clear, binary right and wrong answers. Algorithms work for mathematical calculations, computer code, manufacturing assembly lines, and scientific experiments.
Key benefits are consistency, accuracy, and efficiency. However, they require extensive upfront development and only apply to scenarios with strict parameters. Additionally, human error can lead to mistakes.
For example, crew members of fast food chains like McDonald’s follow specific algorithms for food prep – from grill times to ingredient amounts in sandwiches, to order fulfillment procedures. This ensures uniform quality and service across all locations. However, if a step is missed, errors occur.
The Problem-Solving Process
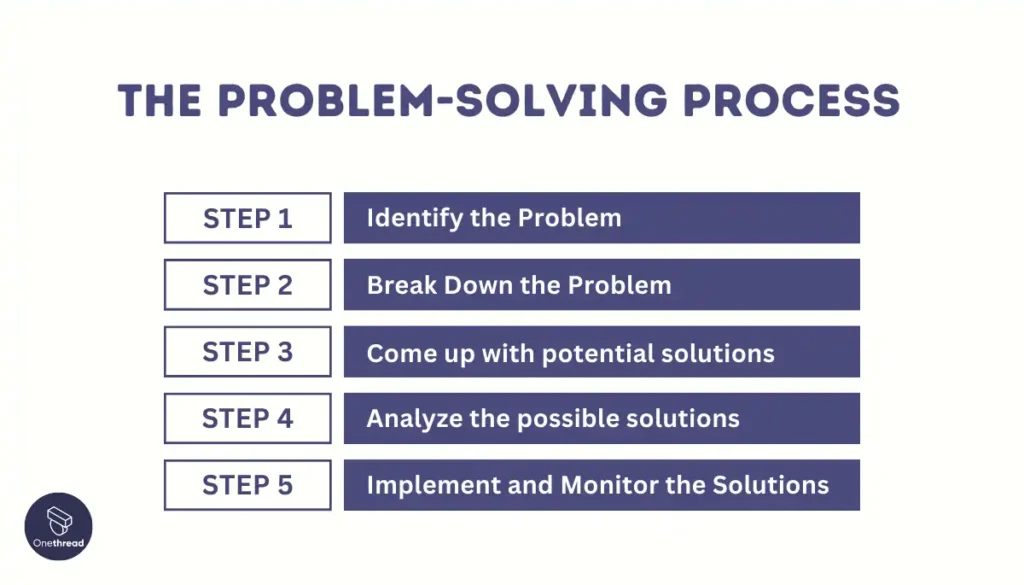
The problem-solving process typically includes defining the issue, analyzing details, creating solutions, weighing choices, acting, and reviewing results.
In the above, we have discussed several problem-solving strategies. For every problem-solving strategy, you have to follow these processes. Here’s a detailed step-by-step process of effective problem-solving:
Step 1: Identify the Problem
The problem-solving process starts with identifying the problem. This step involves understanding the issue’s nature, its scope, and its impact. Once the problem is clearly defined, it sets the foundation for finding effective solutions.
Identifying the problem is crucial. It means figuring out exactly what needs fixing. This involves looking at the situation closely, understanding what’s wrong, and knowing how it affects things. It’s about asking the right questions to get a clear picture of the issue.
This step is important because it guides the rest of the problem-solving process. Without a clear understanding of the problem, finding a solution is much harder. It’s like diagnosing an illness before treating it. Once the problem is identified accurately, you can move on to exploring possible solutions and deciding on the best course of action.
Step 2: Break Down the Problem
Breaking down the problem is a key step in the problem-solving process. It involves dividing the main issue into smaller, more manageable parts. This makes it easier to understand and tackle each component one by one.
After identifying the problem, the next step is to break it down. This means splitting the big issue into smaller pieces. It’s like solving a puzzle by handling one piece at a time.
By doing this, you can focus on each part without feeling overwhelmed. It also helps in identifying the root causes of the problem. Breaking down the problem allows for a clearer analysis and makes finding solutions more straightforward.
Each smaller problem can be addressed individually, leading to an effective resolution of the overall issue. This approach not only simplifies complex problems but also aids in developing a systematic plan to solve them.
Step 3: Come up with potential solutions
Coming up with potential solutions is the third step in the problem-solving process. It involves brainstorming various options to address the problem, considering creativity and feasibility to find the best approach.
After breaking down the problem, it’s time to think of ways to solve it. This stage is about brainstorming different solutions. You look at the smaller issues you’ve identified and start thinking of ways to fix them. This is where creativity comes in.
You want to come up with as many ideas as possible, no matter how out-of-the-box they seem. It’s important to consider all options and evaluate their pros and cons. This process allows you to gather a range of possible solutions.
Later, you can narrow these down to the most practical and effective ones. This step is crucial because it sets the stage for deciding on the best solution to implement. It’s about being open-minded and innovative to tackle the problem effectively.
Step 4: Analyze the possible solutions
Analyzing the possible solutions is the fourth step in the problem-solving process. It involves evaluating each proposed solution’s advantages and disadvantages to determine the most effective and feasible option.
After coming up with potential solutions, the next step is to analyze them. This means looking closely at each idea to see how well it solves the problem. You weigh the pros and cons of every solution.
Consider factors like cost, time, resources, and potential outcomes. This analysis helps in understanding the implications of each option. It’s about being critical and objective, ensuring that the chosen solution is not only effective but also practical.
This step is vital because it guides you towards making an informed decision. It involves comparing the solutions against each other and selecting the one that best addresses the problem.
By thoroughly analyzing the options, you can move forward with confidence, knowing you’ve chosen the best path to solve the issue.
Step 5: Implement and Monitor the Solutions
Implementing and monitoring the solutions is the final step in the problem-solving process. It involves putting the chosen solution into action and observing its effectiveness, making adjustments as necessary.
Once you’ve selected the best solution, it’s time to put it into practice. This step is about action. You implement the chosen solution and then keep an eye on how it works. Monitoring is crucial because it tells you if the solution is solving the problem as expected.
If things don’t go as planned, you may need to make some changes. This could mean tweaking the current solution or trying a different one. The goal is to ensure the problem is fully resolved.
This step is critical because it involves real-world application. It’s not just about planning; it’s about doing and adjusting based on results. By effectively implementing and monitoring the solutions, you can achieve the desired outcome and solve the problem successfully.
Why This Process is Important
Following a defined process to solve problems is important because it provides a systematic, structured approach instead of a haphazard one. Having clear steps guides logical thinking, analysis, and decision-making to increase effectiveness. Key reasons it helps are:
- Clear Direction: This process gives you a clear path to follow, which can make solving problems less overwhelming.
- Better Solutions: Thoughtful analysis of root causes, iterative testing of solutions, and learning orientation lead to addressing the heart of issues rather than just symptoms.
- Saves Time and Energy: Instead of guessing or trying random things, this process helps you find a solution more efficiently.
- Improves Skills: The more you use this process, the better you get at solving problems. It’s like practicing a sport. The more you practice, the better you play.
- Maximizes collaboration: Involving various stakeholders in the process enables broader inputs. Their communication and coordination are streamlined through organized brainstorming and evaluation.
- Provides consistency: Standard methodology across problems enables building institutional problem-solving capabilities over time. Patterns emerge on effective techniques to apply to different situations.
The problem-solving process is a powerful tool that can help us tackle any challenge we face. By following these steps, we can find solutions that work and learn important skills along the way.
Key Skills for Efficient Problem Solving

Efficient problem-solving requires breaking down issues logically, evaluating options, and implementing practical solutions.
Key skills include critical thinking to understand root causes, creativity to brainstorm innovative ideas, communication abilities to collaborate with others, and decision-making to select the best way forward. Staying adaptable, reflecting on outcomes, and applying lessons learned are also essential.
With practice, these capacities will lead to increased personal and team effectiveness in systematically addressing any problem.
Let’s explore the powers you need to become a problem-solving hero!
Critical Thinking and Analytical Skills
Critical thinking and analytical skills are vital for efficient problem-solving as they enable individuals to objectively evaluate information, identify key issues, and generate effective solutions.
These skills facilitate a deeper understanding of problems, leading to logical, well-reasoned decisions. By systematically breaking down complex issues and considering various perspectives, individuals can develop more innovative and practical solutions, enhancing their problem-solving effectiveness.
Communication Skills
Effective communication skills are essential for efficient problem-solving as they facilitate clear sharing of information, ensuring all team members understand the problem and proposed solutions.
These skills enable individuals to articulate issues, listen actively, and collaborate effectively, fostering a productive environment where diverse ideas can be exchanged and refined. By enhancing mutual understanding, communication skills contribute significantly to identifying and implementing the most viable solutions.
Decision-Making
Strong decision-making skills are crucial for efficient problem-solving, as they enable individuals to choose the best course of action from multiple alternatives.
These skills involve evaluating the potential outcomes of different solutions, considering the risks and benefits, and making informed choices. Effective decision-making leads to the implementation of solutions that are likely to resolve problems effectively, ensuring resources are used efficiently and goals are achieved.
Planning and Prioritization
Planning and prioritization are key for efficient problem-solving, ensuring resources are allocated effectively to address the most critical issues first. This approach helps in organizing tasks according to their urgency and impact, streamlining efforts towards achieving the desired outcome efficiently.
Emotional Intelligence
Emotional intelligence enhances problem-solving by allowing individuals to manage emotions, understand others, and navigate social complexities. It fosters a positive, collaborative environment, essential for generating creative solutions and making informed, empathetic decisions.
Leadership skills drive efficient problem-solving by inspiring and guiding teams toward common goals. Effective leaders motivate their teams, foster innovation, and navigate challenges, ensuring collective efforts are focused and productive in addressing problems.
Time Management
Time management is crucial in problem-solving, enabling individuals to allocate appropriate time to each task. By efficiently managing time, one can ensure that critical problems are addressed promptly without neglecting other responsibilities.
Data Analysis
Data analysis skills are essential for problem-solving, as they enable individuals to sift through data, identify trends, and extract actionable insights. This analytical approach supports evidence-based decision-making, leading to more accurate and effective solutions.
Research Skills
Research skills are vital for efficient problem-solving, allowing individuals to gather relevant information, explore various solutions, and understand the problem’s context. This thorough exploration aids in developing well-informed, innovative solutions.
Becoming a great problem solver takes practice, but with these skills, you’re on your way to becoming a problem-solving hero.
How to Improve Your Problem-Solving Skills?

Improving your problem-solving skills can make you a master at overcoming challenges. Learn from experts, practice regularly, welcome feedback, try new methods, experiment, and study others’ success to become better.
Learning from Experts
Improving problem-solving skills by learning from experts involves seeking mentorship, attending workshops, and studying case studies. Experts provide insights and techniques that refine your approach, enhancing your ability to tackle complex problems effectively.
To enhance your problem-solving skills, learning from experts can be incredibly beneficial. Engaging with mentors, participating in specialized workshops, and analyzing case studies from seasoned professionals can offer valuable perspectives and strategies.
Experts share their experiences, mistakes, and successes, providing practical knowledge that can be applied to your own problem-solving process. This exposure not only broadens your understanding but also introduces you to diverse methods and approaches, enabling you to tackle challenges more efficiently and creatively.
Improving problem-solving skills through practice involves tackling a variety of challenges regularly. This hands-on approach helps in refining techniques and strategies, making you more adept at identifying and solving problems efficiently.
One of the most effective ways to enhance your problem-solving skills is through consistent practice. By engaging with different types of problems on a regular basis, you develop a deeper understanding of various strategies and how they can be applied.
This hands-on experience allows you to experiment with different approaches, learn from mistakes, and build confidence in your ability to tackle challenges.
Regular practice not only sharpens your analytical and critical thinking skills but also encourages adaptability and innovation, key components of effective problem-solving.
Openness to Feedback
Being open to feedback is like unlocking a secret level in a game. It helps you boost your problem-solving skills. Improving problem-solving skills through openness to feedback involves actively seeking and constructively responding to critiques.
This receptivity enables you to refine your strategies and approaches based on insights from others, leading to more effective solutions.
Learning New Approaches and Methodologies
Learning new approaches and methodologies is like adding new tools to your toolbox. It makes you a smarter problem-solver. Enhancing problem-solving skills by learning new approaches and methodologies involves staying updated with the latest trends and techniques in your field.
This continuous learning expands your toolkit, enabling innovative solutions and a fresh perspective on challenges.
Experimentation
Experimentation is like being a scientist of your own problems. It’s a powerful way to improve your problem-solving skills. Boosting problem-solving skills through experimentation means trying out different solutions to see what works best. This trial-and-error approach fosters creativity and can lead to unique solutions that wouldn’t have been considered otherwise.
Analyzing Competitors’ Success
Analyzing competitors’ success is like being a detective. It’s a smart way to boost your problem-solving skills. Improving problem-solving skills by analyzing competitors’ success involves studying their strategies and outcomes. Understanding what worked for them can provide valuable insights and inspire effective solutions for your own challenges.
Challenges in Problem-Solving
Facing obstacles when solving problems is common. Recognizing these barriers, like fear of failure or lack of information, helps us find ways around them for better solutions.
Fear of Failure
Fear of failure is like a big, scary monster that stops us from solving problems. It’s a challenge many face. Because being afraid of making mistakes can make us too scared to try new solutions.
How can we overcome this? First, understand that it’s okay to fail. Failure is not the opposite of success; it’s part of learning. Every time we fail, we discover one more way not to solve a problem, getting us closer to the right solution. Treat each attempt like an experiment. It’s not about failing; it’s about testing and learning.
Lack of Information
Lack of information is like trying to solve a puzzle with missing pieces. It’s a big challenge in problem-solving. Because without all the necessary details, finding a solution is much harder.
How can we fix this? Start by gathering as much information as you can. Ask questions, do research, or talk to experts. Think of yourself as a detective looking for clues. The more information you collect, the clearer the picture becomes. Then, use what you’ve learned to think of solutions.
Fixed Mindset
A fixed mindset is like being stuck in quicksand; it makes solving problems harder. It means thinking you can’t improve or learn new ways to solve issues.
How can we change this? First, believe that you can grow and learn from challenges. Think of your brain as a muscle that gets stronger every time you use it. When you face a problem, instead of saying “I can’t do this,” try thinking, “I can’t do this yet.” Look for lessons in every challenge and celebrate small wins.
Everyone starts somewhere, and mistakes are just steps on the path to getting better. By shifting to a growth mindset, you’ll see problems as opportunities to grow. Keep trying, keep learning, and your problem-solving skills will soar!
Jumping to Conclusions
Jumping to conclusions is like trying to finish a race before it starts. It’s a challenge in problem-solving. That means making a decision too quickly without looking at all the facts.
How can we avoid this? First, take a deep breath and slow down. Think about the problem like a puzzle. You need to see all the pieces before you know where they go. Ask questions, gather information, and consider different possibilities. Don’t choose the first solution that comes to mind. Instead, compare a few options.
Feeling Overwhelmed
Feeling overwhelmed is like being buried under a mountain of puzzles. It’s a big challenge in problem-solving. When we’re overwhelmed, everything seems too hard to handle.
How can we deal with this? Start by taking a step back. Breathe deeply and focus on one thing at a time. Break the big problem into smaller pieces, like sorting puzzle pieces by color. Tackle each small piece one by one. It’s also okay to ask for help. Sometimes, talking to someone else can give you a new perspective.
Confirmation Bias
Confirmation bias is like wearing glasses that only let you see what you want to see. It’s a challenge in problem-solving. Because it makes us focus only on information that agrees with what we already believe, ignoring anything that doesn’t.
How can we overcome this? First, be aware that you might be doing it. It’s like checking if your glasses are on right. Then, purposely look for information that challenges your views. It’s like trying on a different pair of glasses to see a new perspective. Ask questions and listen to answers, even if they don’t fit what you thought before.
Groupthink is like everyone in a group deciding to wear the same outfit without asking why. It’s a challenge in problem-solving. It means making decisions just because everyone else agrees, without really thinking it through.
How can we avoid this? First, encourage everyone in the group to share their ideas, even if they’re different. It’s like inviting everyone to show their unique style of clothes.
Listen to all opinions and discuss them. It’s okay to disagree; it helps us think of better solutions. Also, sometimes, ask someone outside the group for their thoughts. They might see something everyone in the group missed.
Overcoming obstacles in problem-solving requires patience, openness, and a willingness to learn from mistakes. By recognizing these barriers, we can develop strategies to navigate around them, leading to more effective and creative solutions.
What are the most common problem-solving techniques?
The most common techniques include brainstorming, the 5 Whys, mind mapping, SWOT analysis, and using algorithms or heuristics. Each approach has its strengths, suitable for different types of problems.
What’s the best problem-solving strategy for every situation?
There’s no one-size-fits-all strategy. The best approach depends on the problem’s complexity, available resources, and time constraints. Combining multiple techniques often yields the best results.
How can I improve my problem-solving skills?
Improve your problem-solving skills by practicing regularly, learning from experts, staying open to feedback, and continuously updating your knowledge on new approaches and methodologies.
Are there any tools or resources to help with problem-solving?
Yes, tools like mind mapping software, online courses on critical thinking, and books on problem-solving techniques can be very helpful. Joining forums or groups focused on problem-solving can also provide support and insights.
What are some common mistakes people make when solving problems?
Common mistakes include jumping to conclusions without fully understanding the problem, ignoring valuable feedback, sticking to familiar solutions without considering alternatives, and not breaking down complex problems into manageable parts.
Final Words
Mastering problem-solving strategies equips us with the tools to tackle challenges across all areas of life. By understanding and applying these techniques, embracing a growth mindset, and learning from both successes and obstacles, we can transform problems into opportunities for growth. Continuously improving these skills ensures we’re prepared to face and solve future challenges more effectively.

Let's Get Started with Onethread
Onethread empowers you to plan, organise, and track projects with ease, ensuring you meet deadlines, allocate resources efficiently, and keep progress transparent.
By subscribing you agree to our Privacy Policy .
Giving modern marketing teams superpowers with short links that stand out.
- Live Product Demo
© Copyright 2023 Onethread, Inc

How To Solve Complex Problems
In today’s increasingly complex world, we are constantly faced with ill-defined problems that don’t have a clear solution. From poverty and climate change to crime and addiction, complex situations surround us. Unlike simple problems with a pre-defined or “right” answer, complex problems share several basic characteristics that make them hard to solve. While these problems can be frustrating and overwhelming, they also offer an opportunity for growth and creativity. Complex problem-solving skills are the key to addressing these tough issues.
In this article, I will discuss simple versus complex problems, define complex problem solving, and describe why it is so important in complex dynamic environments. I will also explain how to develop problem-solving skills and share some tips for effectively solving complex problems.
How is simple problem-solving different from complex problem-solving?
Solving problems is about getting from a currently undesirable state to an intended goal state. In other words, about bridging the gap between “what is” and “what ought to be”. However, the challenge of reaching a solution varies based on the kind of problem that is being solved. There are generally three different kinds of problems you should consider.
Simple problems have one problem solution. The goal is to find that answer as quickly and efficiently as possible. Puzzles are classic examples of simple problem solving. The objective is to find the one correct solution out of many possibilities.
Problems are different from puzzles in that they don’t have a known problem solution. As such, many people may agree that there is an issue to be solved, but they may not agree on the intended goal state or how to get there. In this type of problem, people spend a lot of time debating the best solution and the optimal way to achieve it.
Messes are collections of interrelated problems where many stakeholders may not even agree on what the issue is. Unlike problems where there is agreement about what the problem is, in messes, there isn’t agreement amongst stakeholders. In other words, even “what is” can’t be taken for granted. Most complex social problems are messes, made up of interrelated social issues with ill-defined boundaries and goals.
Problems and messes can be complicated or complex
Puzzles are simple, but problems and messes exist on a continuum between complicated and complex. Complicated problems are technical in nature. There may be many involved variables, but the relationships are linear. As a result, complicated problems have step-by-step, systematic solutions. Repairing an engine or building a rocket may be difficult because of the many parts involved, but it is a technical problem we call complicated.
On the other hand, solving a complex problem is entirely different. Unlike complicated problems that may have many variables with linear relationships, a complex problem is characterized by connectivity patterns that are harder to understand and predict.
Characteristics of complex problems and messes
So what else makes a problem complex? Here are seven additional characteristics (from Funke and Hester and Adams ).
- Lack of information. There is often a lack of data or information about the problem itself. In some cases, variables are unknown or cannot be measured.
- Many goals. A complex problem has a mix of conflicting objectives. In some sense, every stakeholder involved with the problem may have their own goals. However, with limited resources, not all goals can be simultaneously satisfied.
- Unpredictable feedback loops. In part due to many variables connected by a range of different relationships, a change in one variable is likely to have effects on other variables in the system. However, because we do not know all of the variables it will affect, small changes can have disproportionate system-wide effects. These unexpected events that have big, unpredictable effects are sometimes called Black Swans.
- Dynamic. A complex problem changes over time and there is a significant impact based on when you act. In other words, because the problem and its parts and relationships are constantly changing, an action taken today won’t have the same effects as the same action taken tomorrow.
- Time-delayed. It takes a while for cause and effect to be realized. Thus it is very hard to know if any given intervention is working.
- Unknown unknowns. Building off the previous point about a lack of information, in a complex problem you may not even know what you don’t know. In other words, there may be very important variables that you are not even aware of.
- Affected by (error-prone) humans. Simply put, human behavior tends to be illogical and unpredictable. When humans are involved in a problem, avoiding error may be impossible.
What is complex problem-solving?
“Complex problem solving” is the term for how to address a complex problem or messes that have the characteristics listed above.
Since a complex problem is a different phenomenon than a simple or complicated problem, solving them requires a different approach. Methods designed for simple problems, like systematic organization, deductive logic, and linear thinking don’t work well on their own for a complex problem.
And yet, despite its importance, there isn’t complete agreement about what exactly it is.
How is complex problem solving defined by experts?
Let’s look at what scientists, researchers, and system thinkers have come up with in terms of a definition for solving a complex problem.
As a series of observations and informed decisions
For many employers, the focus is on making smart decisions. These must weigh the future effects to the company of any given solution. According to Indeed.com , it is defined as “a series of observations and informed decisions used to find and implement a solution to a problem. Beyond finding and implementing a solution, complex problem solving also involves considering future changes to circumstance, resources, and capabilities that may affect the trajectory of the process and success of the solution. Complex problem solving also involves considering the impact of the solution on the surrounding environment and individuals.”
As using information to review options and develop solutions
For others, it is more of a systematic way to consider a range of options. According to O*NET , the definition focuses on “identifying complex problems and reviewing related information to develop and evaluate options and implement solutions.”
As a self-regulated psychological process
Others emphasize the broad range of skills and emotions needed for change. In addition, they endorse an inspired kind of pragmatism. For example, Dietrich Dorner and Joachim Funke define it as “a collection of self-regulated psychological processes and activities necessary in dynamic environments to achieve ill-defined goals that cannot be reached by routine actions. Creative combinations of knowledge and a broad set of strategies are needed. Solutions are often more bricolage than perfect or optimal. The problem-solving process combines cognitive, emotional, and motivational aspects, particularly in high-stakes situations. Complex problems usually involve knowledge-rich requirements and collaboration among different persons.”
As a novel way of thinking and reasoning
Finally, some emphasize the multidisciplinary nature of knowledge and processes needed to tackle a complex problem. Patrick Hester and Kevin MacG. Adams have stated that “no single discipline can solve truly complex problems. Problems of real interest, those vexing ones that keep you up at night, require a discipline-agnostic approach…Simply they require us to think systemically about our problem…a novel way of thinking and reasoning about complex problems that encourages increased understanding and deliberate intervention.”
A synthesis definition
By pulling the main themes of these definitions together, we can get a sense of what complex problem-solvers must do:
Gain a better understanding of the phenomena of a complex problem or mess. Use a discipline-agnostic approach in order to develop deliberate interventions. Take into consideration future impacts on the surrounding environment.
Why is complex problem solving important?
Many efforts aimed at complex social problems like reducing homelessness and improving public health – despite good intentions giving more effort than ever before – are destined to fail because their approach is based on simple problem-solving. And some efforts might even unwittingly be contributing to the problems they’re trying to solve.
Einstein said that “We can’t solve problems by using the same kind of thinking we used when we created them.” I think he could have easily been alluding to the need for more complex problem solvers who think differently. So what skills are required to do this?
What are complex problem-solving skills?
The skills required to solve a complex problem aren’t from one domain, nor are they an easily-packaged bundle. Rather, I like to think of them as a balancing act between a series of seemingly opposite approaches but synthesized. This brings a sort of cognitive dissonance into the process, which is itself informative.
It brings F. Scott Fitzgerald’s maxim to mind:
“The test of a first-rate intelligence is the ability to hold two opposing ideas in mind at the same time and still retain the ability to function. One should, for example, be able to see that things are hopeless yet be determined to make them otherwise.”
To see the problem situation clearly, for example, but also with a sense of optimism and possibility.
Here are the top three dialectics to keep in mind:
Thinking and reasoning
Reasoning is the ability to make logical deductions based on evidence and counterevidence. On the other hand, thinking is more about imagining an unknown reality based on thoughts about the whole picture and how the parts could fit together. By thinking clearly, one can have a sense of possibility that prepares the mind to deduce the right action in the unique moment at hand.
As Dorner and Funke explain: “Not every situation requires the same action, and we may want to act this way or another to reach this or that goal. This appears logical, but it is a logic based on constantly shifting grounds: We cannot know whether necessary conditions are met, sometimes the assumptions we have made later turn out to be incorrect, and sometimes we have to revise our assumptions or make completely new ones. It is necessary to constantly switch between our sense of possibility and our sense of reality, that is, to switch between thinking and reasoning. It is an arduous process, and some people handle it well, while others do not.”
Analysis and reductionism combined with synthesis and holism
It’s important to be able to use scientific processes to break down a complex problem into its parts and analyze them. But at the same time, a complex problem is more than the sum of its parts. In most cases, the relationships between the parts are more important than the parts themselves. Therefore, decomposing problems with rigor isn’t enough. What’s needed, once problems are reduced and understood, is a way of understanding the relationships between various components as well as putting the pieces back together. However, synthesis and holism on their own without deductive analysis can often miss details and relationships that matter.
What makes this balancing act more difficult is that certain professions tend to be trained in and prefer one domain over the other. Scientists prefer analysis and reductionism whereas most social scientists and practitioners default to synthesis and holism. Unfortunately, this divide of preferences results in people working in their silos at the expense of multi-disciplinary approaches that together can better “see” complexity.
Situational awareness and self-awareness
Dual awareness is the ability to pay attention to two experiences simultaneously. In the case of complex problems, context really matters. In other words, problem-solving exists in an ecosystem of environmental factors that are not incidental. Personal and cultural preferences play a part as do current events unfolding over time. But as a problem solver, knowing the environment is only part of the equation.
The other crucial part is the internal psychological process unique to every individual who also interacts with the problem and the environment. Problem solvers inevitably come into contact with others who may disagree with them, or be advancing seemingly counterproductive solutions, and these interactions result in emotions and motivations. Without self-awareness, we can become attached to our own subjective opinions, fall in love with “our” solutions, and generally be driven by the desire to be seen as problem solvers at the expense of actually solving the problem.
By balancing these three dialectics, practitioners can better deal with uncertainty as well as stay motivated despite setbacks. Self-regulation among these seemingly opposite approaches also reminds one to stay open-minded.
How do you develop complex problem-solving skills?
There is no one answer to this question, as the best way to develop them will vary depending on your strengths and weaknesses. However, there are a few general things that you can do to improve your ability to solve problems.
Ground yourself in theory and knowledge
First, it is important to learn about systems thinking and complexity theories. These frameworks will help you understand how complex systems work, and how different parts of a system interact with each other. This conceptual understanding will allow you to identify potential solutions to problems more quickly and effectively.
Practice switching between approaches
Second, practice switching between the dialectics mentioned above. For example, in your next meeting try to spend roughly half your time thinking and half your time reasoning. The important part is trying to get habituated to regularly switching lenses. It may seem disjointed at first, but after a while, it becomes second nature to simultaneously see how the parts interact and the big picture.
Focus on the specific problem phenomena
Third, it may sound obvious, but people often don’t spend very much time studying the problem itself and how it functions. In some sense, becoming a good problem-solver involves becoming a problem scientist. Your time should be spent regularly investigating the phenomena of “what is” rather than “what ought to be”. A holistic understanding of the problem is the required prerequisite to coming up with good solutions.
Stay curious
Finally, after we have worked on a problem for a while, we tend to think we know everything about it, including how to solve it. Even if we’re working on a problem, which may change dynamically from day to day, we start treating it more like a puzzle with a definite solution. When that happens, we can lose our motivation to continue learning about the problem. This is very risky because it closes the door to learning from others, regardless of whether we completely agree with them or not.
As Neils Bohr said, “Two different perspectives or models about a system will reveal truths regarding the system that are neither entirely independent nor entirely compatible.”
By staying curious, we can retain our ability to learn on a daily basis.
Tips for how to solve complex problems
Focus on processes over results.
It’s easy to get lost in utopian thinking. Many people spend so much time on “what ought to be” that they forget that problem solving is about the gap between “what is” and “what ought to be”. It is said that “life is a journey, not a destination.” The same is true for complex problem-solving. To do it well, a problem solver must focus on enjoying the process of gaining a holistic understanding of the problem.
Adaptive and iterative methods and tools
A variety of adaptive and iterative methods have been developed to address complexity. They share a laser focus on gaining holistic understanding with tools that best match the phenomena of complexity. They are also non-ideological, trans-disciplinary, and flexible. In most cases, your journey through a set of steps won’t be linear. Rather, as you think and reason, analyze and synthesize, you’ll jump around to get a holistic picture.
In my online course , we generally follow a seven-step method:
- Get clear sight with a complex problem-solving frame
- Establish a secure base of operation
- Gain a deep understanding of the problem
- Create an interactive model of the problem
- Develop an impact strategy
- Create an action plan and implement
- Embed systemic solutions
Of course, each of these steps involves testing to see what works and consistently evaluating our process and progress.
Resolution is about systematically managing a problem over time
One last thing to keep in mind. Most social problems are not just solved one day, never to return. In reality, most complex problems are managed, not solved. For all practical purposes, what this means is that “the solution” is a way of systematically dealing with the problem over time. Some find this disappointing, but it’s actually a pragmatic pointer to think about resolution – a way move problems in the right direction – rather than final solutions.
Problem solvers regularly train and practice
If you need help developing your complex problem-solving skills, I have an online class where you can learn everything you need to know.
Sign up today and learn how to be successful at making a difference in the world!
SoftwareDominos

The 7 Timeless Steps to Guide You Through Complex Problem Solving
I. Introduction
As we go through life, we inevitably encounter problems that require extensive forethought, critical thinking , and creativity . Solving complex problems is a crucial skill for success, whether it’s a business challenge, a personal dilemma, or a societal issue.
This guide will explore the fundamentals of complex problem-solving and provide practical tips and strategies for mastering this critical skill.
II. This Series Also Discusses…
This article is part of a series on complex problem-solving. The list below will guide you through the different subtopics.
Complex Problem-Solving Guide in 7 Steps
The Nature of Complex Problems
What Does the Nature of the Problem Tell Us About Its Solution
Gaussian Distributions vs Power Laws
Your Ultimate Guide to Making Sense of Natural and Social Phenomena
Complex Problem-Solving in Groups
An Exploratory Overview of ProbleSolving Processes in Groups
The Power of Critical Thinking
An Essential Guide for Personal and Professional Development
Group-Decision Making
6 Modes That Tell Us How Teams Decide
III. What Is a Complex Problem?
A. generic definition of complex problems.
Four properties allow us to distinguish complex problems from simple ones.
- Complex problems accept alternative solutions
- Choices can weighed in multiple ways
- Data supports multiple hypotheses
- Breakdown of causal chains.
In crude terms, a complex problem presents no trivial or obvious solution. In other words, it shows the following characteristics:
Now that we have defined the general notion of a complex problem let’s examine some specific cases related to software development , business management , and complexity theory.
B. Examples of Complex Problems
1. complex problems in software development.
A complex software development problem involves intricate interactions between numerous system components and requires a sophisticated understanding of the business problem, computing , algorithms and data structures.
Source: “Domain-Driven Design: Tackling Complexity in the Heart of Software” by Eric Evans
2. Complex Problems in Business Management
In business management , a complex problem is characterized by interconnected elements, uncertainty, and dynamic interactions, making it challenging to predict outcomes and devise straightforward solutions. This is most obviously seen in formulating effective organisational strategies or leading successful enterprise transformations.
Source: “ Strategic Management and Organisational Dynamics: The Challenge of Complexity ” by Ralph D. Stacey
3. Complex Problems in Complexity Theory
From a complexity theory standpoint, a complex problem involves many interacting agents or components, often exhibiting emergent properties that cannot be easily deduced from the properties of individual agents.
Source: “ The Quark and the Jaguar: Adventures in the Simple and the Complex ” by Murray Gell-Mann
Complex problems are contrasted with complicated problems. Complicated problems have clear causes and effects, can be broken down into smaller parts, and have predictable solutions. Complex problems, however, are dynamic, have interconnected parts, and exhibit emergent properties (unpredictable outcomes from the interaction of parts).
Source: “Cynefin Framework” (2007) by Dave Snowden
C. What are Complex Problem Solving Skills?
Complex problem-solving skills involve identifying , analysing , and solving non-routine problems requiring high cognitive effort.
These problems typically involve a large number of variables and require the application of creative and critical thinking skills to identify potential solutions. Individuals with complex problem-solving skills can work through ambiguity and uncertainty and use logical reasoning to develop effective solutions.
IV. Solving Complex Problems: A Generic Approach
While developing a universal solution that works in any context would be very challenging, we will describe a generic approach consisting of seven steps that will assist you in creating a bespoke method suitable to the specific context you are working in.
At the heart of this approach is logical decomposition , or breaking down a complex problem into smaller, more manageable ones and then developing and implementing effective solutions for each. This skill is essential for success in many areas of life, including business, education , and personal relationships.
Logical decomposition is at the heart of scientific thought, as described in Edsger W. Dijkstra’s paper “ On the Role of Scientific Thought “.
The seven steps to solving complex problems are listed below. We will go through them in great detail in the following sections.

The 7 steps to creative solutions
V. Complex Problem-Solving Skills
A. why are complex problem solving skills essential.
In today’s rapidly changing world, individuals and organizations must possess complex problem-solving skills to succeed. These skills are essential for several reasons:
Dealing with Uncertainty
In many situations, there is no clear-cut solution to a problem. Complex problem-solving skills enable individuals to work through ambiguity and uncertainty and develop effective solutions.
Identifying Root Causes
Complex problems often have multiple causes that are difficult to identify. Individuals with complex problem-solving skills can identify and address the root causes of problems rather than just treating the symptoms.
Developing Creative Solutions
Complex problems require creative solutions that go beyond traditional approaches. Individuals who possess complex problem-solving skills can think outside the box and develop innovative solutions.
Achieving Business Success
Organizations with complex problem-solving skills are better equipped to overcome challenges, identify opportunities, and succeed in today’s competitive business environment.
B. How to Develop Complex Problem-Solving Skills
While some individuals possess a natural aptitude for complex problem-solving, these skills can be developed and improved over time. Here are some tips to help you develop complex problem-solving skills:
1. Build Your Knowledge Base
Developing complex problem-solving skills requires a strong foundation of knowledge in your area of expertise. Stay updated on your field’s latest trends, research, and developments to enhance your problem-solving abilities.
2. Practice Critical Thinking
Developing critical thinking skills is essential for complex problem-solving. Practice questioning assumptions, analyzing information , and evaluating arguments to develop critical thinking skills.
3. Embrace Creativity
Complex problems require creative solutions. Embrace your creativity by exploring new ideas, brainstorming solutions, and seeking diverse perspectives.
4. Collaborate with Others
Collaborating with others can help you develop your complex problem-solving skills. Working in a team environment can expose you to new ideas and approaches, help you identify blind spots, and provide opportunities for feedback and support.
5. Seek Out Challenging Problems
Developing complex problem-solving skills requires practice. Seek out challenging problems and apply your problem-solving skills to real-world situations.
VI. Step 1: Understanding the Nature of Complex vs Complicated
A. the cynefin framework.
Complex and complicated problems are two distinct types of challenges that require different approaches to solve. Dave Snowden, a management consultant and researcher, developed the Cynefin framework, a conceptual model used to understand complex systems and situations. The framework identifies five domains: simple, complicated, complex, chaotic, and disordered, and guides how to approach challenges in each domain.
B. Complicated Problems

Complicated Problems:
- are characterized by having many interrelated parts and require specialized knowledge and expertise to solve.
- have a clear cause-and-effect relationship , and the solution can be discovered by systematically analysing the components.
- are best addressed through a top-down, expert-driven approach , where the experts can identify the best solution through analysis and evaluation.
C. Complex Problems
Complex problems are characterized by uncertainty, ambiguity, and the involvement of multiple interconnected factors. There is no clear cause-and-effect relationship, and the solution cannot be found by simply analysing the components. Complex problems require a bottom-up, participatory approach, where multiple perspectives and ideas are considered to develop a solution. The solution may not be clear initially but involves experimentation, adaptation, and feedback.
The Cynefin framework proposes that complex problems belong to the complex domain, where emergent solutions cannot be predicted or prescribed. The complex domain should explore the problem, generate hypotheses, and test them through experimentation. The emphasis is on learning from the process , adapting to changing circumstances, and using feedback to guide the solution.
D. Practical Tips on Identifying an Appropriate Framework
Objective — Classify the problem as complex, complicated, or disordered. This classification will determine the approach to be used.
How it’s done — You can do that by asking the following questions.
- Do we have multiple, internally consistent, competing hypotheses explaining the issue?
- Does the available data support both theories?
In this case, the problem lies in the complex domain, and the preferred approach is to identify good solutions and conduct safe-to-fail experiments. If it’s a complicated (but not complex) problem, the following questions can be answered in the affirmative:
- Do we have a single view that explains the problem?
- Do we know the engineering part of the solution?
- Is the problem sufficiently familiar to be solved by an expert?
VII. Step 2: Identifying and Defining the Problem
A. problem identification.
The first step in problem-solving is identifying the problem. This step involves recognizing that a problem exists and understanding its nature. Some tips for identifying the problem include:
Once you have identified the problem, the next step is to define it. This step involves breaking down the problem into smaller parts and better understanding its nature. Some tips for defining the problem include:
- Writing it down: Write down the problem statement clearly and concisely. This will help you to focus on the specific issue and avoid confusion.
- Breaking it down: Break the problem into smaller parts to better understand its nature. This can help you to identify the underlying causes and potential solutions. The logical decomposition of the issues is vital, and we have dedicated the next section.
- Identifying the scope: Identify the scope of the problem and determine its impact. This can help you to prioritize the problem and allocate resources accordingly.
Reliable data and statistical analysis skills are crucial in problem-solving. Data provides information and insights necessary for understanding the root cause of the problem. Statistical analysis allows us to make sense of the data and extract meaningful information. This article will discuss the importance of reliable data and statistical analysis skills in problem identification.
B. Practical Tips on Identifying the Problem
Objective — Paint a full picture of the problem by laying out the details, preferably on a piece of paper, classifying it, and deciding on an approach to solving it.
How it’s done — Write down a complete description of the problem, including its scope and impact on the various stakeholders or aspects of the business. Use data as evidence to support initial hypotheses. Find out if the problem is localised and can be resolved locally or whether it might need escalation and support from higher levels of management.
VIII. Step 3: Gathering and Analyzing Data
A. gathering reliable data.
In today’s fast-paced business environment, reliable data is more critical than ever. It is vital to have accurate and objective information to identify problems and determine their root cause.

Without reliable data, it is difficult to make informed decisions that can lead to effective problem-solving. Here are some of the benefits of using reliable data in problem identification:
- Objective information: Reliable data provides an objective perspective of the situation.
- Evidence-based decision-making: Using reliable data ensures that decisions are based on evidence rather than assumptions or opinions.
- Improved accuracy: Reliable data improves the accuracy of problem identification, leading to better solutions.
- Better understanding: Reliable data provides a better understanding of the situation, leading to a more comprehensive and holistic approach to problem-solving.
- Improved Risk Management : Reliable helps put problems into perspective by allowing analysts to calculate their occurrence probabilities and impacts. Based on impact and probability , risk can then be categorised and prioritized.
B. Statistical Analysis Skills
Statistical analysis skills are necessary for making sense of the data and extracting meaningful information. These skills allow us to identify patterns and trends, understand the relationships between different variables, and (sometimes) predict future outcomes.

Some benefits of using statistical analysis skills in problem identification include the following:
- Identifying patterns: Statistical analysis skills enable us to identify patterns and trends in the data, which can help identify the problem accurately.
- Understanding relationships: Statistical analysis skills help us understand the relationships between different variables, which can help identify the problem’s root cause.
- Predictive capabilities: Statistical analysis skills allow us to predict future outcomes based on the data, which can help develop effective solutions.
- Objective analysis: Statistical analysis provides objective data analysis, which can help make evidence-based decisions.
Interpreting data, however, requires technical skills to avoid misinterpretations. The following is a common list of statistical analysis mistakes non-professionals can make.
C. How Software Team Leads Can Gather Reliable Data
Software team leads need reliable data on their performance to make informed decisions and identify areas for improvement. Here are some sources where software team leads can gather reliable data on their team’s performance:
- Project management tools: Most project management tools have built-in reporting features, allowing team leads to track performance metrics such as task completion rates, sprint velocity, and burn-down charts. This data can be used to identify areas for improvement and make data-driven decisions.
- Team feedback: Gathering feedback from team members through one-on-one meetings or anonymous feedback forms can provide valuable insights into team performance . This data can help team leads identify areas where team members may struggle or additional training or resources may be needed. Crucially, it also provides insights into the organisational culture .
- Code analysis tools like SonarQube or Code Climate can provide insights into code quality , maintainability, and security. This data can help team leads identify needed code improvements and prioritize technical debt reduction.
- Customer feedback: Customer feedback, such as ratings, reviews, and support tickets, can provide insights into the usability and functionality of deployed applications. This data can help team leads identify areas for improvement and prioritize feature development.
The software team should gather data from multiple sources, use that data to inform decisions and identify areas for improvement. By using reliable data sources and monitoring team performance metrics regularly, software team leads can drive continuous improvement and ensure project success.
D. Practical Tips on Gathering Data to Support the Proposed Hypotheses
Objective — The availability of data can help place the problem into perspective. For example, a dollar figure of the losses due to process inefficiencies can help identify the potential solutions that management will deem feasible.
How it’s done — All modern project management and tracking tools have sophisticated built-in data capture tools that can be exported, cleaned, and analysed for insights.
For example, when evaluating a team’s productivity , you can export data from JIRA, Jenkins, or BitBucket and measure performance metrics such as team velocity, overruns, and time-to-market.
When evidence is insufficient, you can gather more data, abandon the hypothesis, or temporarily shelve it.
IX. Step 4: Logical Decomposition in Problem Solving
A. logical decomposition.
Logical decomposition is a problem-solving technique that breaks down complex problems into smaller, more manageable pieces. It is a structured approach that enables individuals to examine a problem from multiple angles, identify key issues and sub-problems, and develop a solution that addresses each piece of the problem.
The process of logical decomposition involves breaking down the main problem into smaller sub-problems, which are then broken down into smaller pieces. Each piece is analyzed in detail to determine its underlying cause-and-effect relationships and potential solutions. By breaking down the problem into smaller pieces, the individual can better understand the overall problem, identify potential solutions more quickly, and prioritize which sub-problems to address first.
Logical decomposition is particularly useful for dealing with complex issues. It allows individuals to break down a large, overwhelming problem into smaller, more manageable pieces. This not only makes the problem easier to understand and solve but also less daunting and more approachable. Additionally, by breaking down the problem into smaller pieces, individuals can identify and focus on the underlying root causes of the problem rather than just treating the symptoms.
Logical decomposition is a vital stage of architecting large systems and solutions.
B. Practical Tips on Logical Decomposition
Objective — Most problems worth tackling are also overwhelming in size and complexity (or complicatedness). Luckily, a logical decomposition into specialized areas or modules will help focus the team’s efforts on a small enough subproblem or bring in the right expertise.
How it’s done — This author prefers mindmaps. A mindmap is a tree that starts with a single node and branches off into different areas, views, or perspectives of the problem. Mindmaps help analysts stay focused on a key area and ensure that all aspects of a problem are covered.
Once a mindmap has been created, potential solutions can be explored.
From Abstract Concepts to Tangible Value: Solution Architecture in Modern IT Systems
X. Step 5: Generating and Evaluating (Several) Potential Solutions
Generating multiple solutions to solve a problem is an effective way to increase creativity and innovation in problem-solving. By exploring different options, individuals can identify the strengths and weaknesses of each solution and determine the most effective approach to solving the problem. This section will discuss the advantages and techniques of generating multiple solutions to solve problems more effectively.

A. Advantages of Generating Multiple Solutions
The advantages of generating multiple solutions during problem-solving are:
B. Techniques for Generating Multiple Solutions
Techniques for generating multiple solutions:
C. Practical Tips on Solution Generation and Selection
Objective — The key principle of solution generation is comprehensively exploring the solution space. This exploration allows teams to avoid local minima or overcommitting to a suboptimal solution.
How it’s done — The most effective approach is to bring in several people from different areas of expertise or seniority and to offer every suggestion the opportunity to be heard and thoroughly explored.
Also, different stakeholders might favour solutions that maximise their (potentially) narrow gains. If not consulted, they might actively block the implementation of the selected solution if it adversely impacts their interests.
The technical aspect of problem-solving is relatively easy to generate and implement without budgetary or scheduling constraints . It’s only when you consider the cost and impact of a solution that complexity arises.
5 Key Concepts You Need to Know From Herbert Simon’s Paper on the Architecture of Complexity
XI. Step 6: Implementing and Assessing Solutions
Implementing solutions to complex problems requires a structured approach that considers the unique challenges and variables involved. Effective problem-solving involves implementing practical, feasible, and sustainable solutions.
This section will first discuss two approaches to implementing solutions to complex problems: small, safe-to-fail solutions and solving easy problems with enormous benefits.
A. Implementing Many Safe-to-Fail Solutions
One practical approach to implementing solutions to complex problems is small, safe-to-fail solutions. This technique involves implementing a small-scale solution that can be tested quickly and easily to gather feedback.

Starting with small-scale solutions allows individuals to gather feedback and adjust before investing significant resources in a more extensive solution. This approach can save time and resources while ensuring that the final solution meets the needs of stakeholders.
Small safe-to-fail experiments effectively deal with complexity where an engineering solution is unknown priori.
B. Prioritizing High-Yield Solutions
Another effective approach to implementing solutions to complex problems is to first solve easy problems with large benefits. This technique involves identifying and solving simple, straightforward problems that significantly impact the overall problem.
By prioritising easy problems, individuals can progress quickly and gain momentum towards solving the larger problem. This approach can also help build trust and credibility with stakeholders, as progress is visible and measurable.
C. A Systematic Approach to Implementing Solutions
It is important to note that both approaches should be used with a broader problem-solving methodology . Effective problem-solving requires a systematic approach that involves identifying the problem, gathering information, analyzing data, developing and evaluating potential solutions, and implementing the best solution. By implementing small, safe-to-fail solutions and solving easy problems with large benefits, individuals can enhance their problem-solving approach and increase the likelihood of success.
In conclusion, implementing solutions to complex problems requires a structured approach that considers the unique challenges and variables involved. Implementing small, safe-to-fail solutions and solving easy problems with large benefits are two effective techniques for enhancing problem-solving. These techniques should be used with a broader problem-solving methodology to ensure the final solution is practical, feasible, and sustainable.
D. Implementing the Solution
Objective — This stage aims to efficiently and effectively implement the (optimal) selected solution(s).
How it’s done — Three principal techniques are required for the implementation of the solution to succeed. The first is conducting safe-to-fail experiments. The second is allocating resources to conduct each experiment. The third is setting up the criteria for success or failure.
XII. Step 7: Evaluating the Solution
Objective — Solutions might work well under laboratory conditions but fail spectacularly in the field. Evaluating solutions after a trial is vital to avoid continuing investment in failed solutions.
How it’s done — The best way to evaluate a solution is to monitor the Key Performance Indicators (KPIs) originally used in the problem diagnosis. When solutions are successful, noticeable and measurable improvements should be observed.
Measuring second-order effects or observing undesirable team or business dynamics changes is key to continuing or aborting initiatives.
Complex problem-solving refers to the ability to solve complex, ambiguous problems that often require creative and innovative solutions. It involves identifying the root cause of a problem, analyzing different variables and factors, developing and evaluating possible solutions, and selecting the best course of action.
Complex problem-solving is essential because it allows individuals and organizations to overcome challenges and obstacles hindering their progress and success. It enables them to identify opportunities, improve processes, and innovate to stay ahead of the competition.
To develop your complex problem-solving skills, you can practice consistently, develop a systematic approach, and leverage the right tools and resources. You can also seek feedback from others, learn from your mistakes, and adopt a growth mindset that values continuous learning and improvement.
Some common obstacles to effective problem-solving include cognitive biases , lack of information, unclear objectives, and groupthink. These obstacles can hinder individuals and teams from developing effective solutions to complex problems.
Various tools and techniques for complex problem-solving include root cause analysis, fishbone diagrams, SWOT analysis, Pareto analysis, decision trees, and scenario planning. These tools can help individuals and teams to analyze complex problems, identify underlying causes, and develop effective solutions.
To improve your decision-making skills, you can develop a structured approach, gather and analyze relevant data, evaluate different options, and consider each alternative’s potential risks and benefits. You can also seek feedback from others and reflect on your past decisions to learn from your mistakes.
Complex problem-solving skills can be applied in various aspects of your personal life, such as improving your relationships, managing your finances, and achieving your goals. You can overcome obstacles and succeed personally by systematically analyzing different variables and factors and developing creative and innovative solutions.
To overcome cognitive biases in problem-solving, you can challenge your assumptions, seek diverse perspectives, and use data and evidence to inform your decisions. You can also use brainstorming and mind-mapping techniques to generate new ideas and avoid tunnel vision.
XIV. Final Words
In conclusion, complex problem-solving is a crucial skill that can significantly impact your professional and personal life. It allows you to navigate complex challenges, identify the root cause of a problem, and develop practical solutions.
By mastering the art of complex problem-solving, you can enhance your critical thinking, analytical skills, and decision-making abilities, which are essential for success in today’s fast-paced and dynamic business environment.
The key to mastering complex problem-solving is to practice consistently, develop a systematic approach, and leverage the right tools and resources. With patience, persistence, and a growth mindset, anyone can become a skilled problem solver and tackle even the most challenging problems.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.
Breaking Down Complex Math Problems: A Step-by-Step Guide
Understanding complex math problems is essential for students, teachers, and individuals keen on applying math in daily life or at work. Here’s a step-by-step guide to help you dissect and tackle these seemingly daunting equations or problems.
Step 1: Understand the Problem
Before anything else, understand what the problem is asking. To do this, you’ll need to:
- Read the problem carefully, making sure to consider all the provided information.
- Identify what you need to find (this will often be clearly stated in the problem).
- Pinpoint any vocabulary or concepts that you may not understand and look them up.
Let’s take the problem, “If the sum of two consecutive numbers is 27, what are the numbers?” The goal here is to identify the two numbers. The term ‘consecutive’ is vital; it tells us that if one number is n, the next is n+1.
Step 2: Devise a Plan
Creating a plan involves deciding the methods or formulas to use to solve the problem. It may also include deciding the order in which to perform certain operations or steps.
For our problem, we know that consecutive numbers can be represented as n and n+1. The problem tells us their sum is 27. So, we set up the equation: n + (n + 1) = 27.
Step 3: Carry Out the Plan
At this point, we execute the plan we devised in step 2. Here, we solve the equation:
- Combine like terms: 2n + 1 = 27
- Subtract 1 from both sides: 2n = 26
- Divide both sides by 2: n = 13
After we found n, we also need to find n+1, which equals 14. So, the two consecutive numbers are 13 and 14.
Step 4: Check Your Work
Checking the work ensures that the answer is reasonable and fits the criteria of the problem. Here, we check by substituting the numbers back into the original problem. Is 13 + 14 equal to 27? Yes, so we know our solution is correct.
Step 5: Reflect on Your Work
Reflection involves thinking about how you approached the problem, what strategies worked, what didn’t, and why. Reflecting helps improve your problem-solving skills for future problems.
Now let’s try a more complex problem:
“In a basketball game, if Player A scored twice as many points as Player B, and together they scored 54 points, how many points did each player score?”
We are looking for the points each player scored. We know that Player A scored twice as many points as Player B and that they scored 54 points together.
Let’s represent Player B’s score as ‘x’. Given that Player A scored twice as many points, we can represent his score as ‘2x’. Their combined score is 54 points. So, we can create the equation: x + 2x = 54.
Solve the equation:
Combine like terms: 3x = 54
Divide both sides by 3: x = 18
Player B scored 18 points. Since Player A scored twice as many points, he scored 36 points.
Substitute the numbers back into the original problem. Does 18 (Player B’s points) + 36 (Player A’s points) equal 54? Yes, so our solution is correct.
Just as with the simpler problem, reflect on your work. Understanding your own process can make tackling similar problems easier in the future.
In conclusion, breaking down complex math problems doesn’t have to be intimidating. By taking the time to understand the problem, devise a plan, carry out that plan, and then check and reflect on your work, you can effectively solve complex math problems. And remember, practice makes perfect! The more problems you solve, the better you will become.
Now, let’s take a look at a complex word problem that involves quadratic equations – a critical concept in algebra.
“A rectangle has a length that is 2 more than 3 times the width. The area of the rectangle is 75 square units. What are the dimensions of the rectangle?”
Our task is to find the width and length of the rectangle. We know from the problem that:
- The length is 2 more than 3 times the width. If we represent the width as ‘w’, then the length is ‘3w + 2’.
- The area of the rectangle is 75. The formula for the area of a rectangle is ‘width * length’.
We have two equations and two unknowns, which is a good start. Let’s set up our equations:
- L = 3w + 2 (from the first piece of information)
- L * w = 75 (from the second piece of information)
We can substitute the first equation into the second one because they both equal ‘L’.
This results in a quadratic equation:
(3w + 2) * w = 75 3w^2 + 2w = 75 3w^2 + 2w - 75 = 0
The next step is to solve this quadratic equation. Since it’s a quadratic equation, we can use the quadratic formula:
w = [-b ± sqrt(b^2 - 4ac)] / (2a)
In our equation, a = 3, b = 2, and c = -75. Plug those values into the formula:
w = [-2 ± sqrt((2)^2 - 4*3*(-75))] / (2*3) w = [-2 ± sqrt(4 + 900)] / 6 w = [-2 ± sqrt(904)] / 6
The square root of 904 is approximately 30.07. So the two possible values for w are:
w = [-2 + 30.07] / 6 = 4.68 (approximately) w = [-2 - 30.07] / 6 = -5.35 (approximately)
Since we can’t have a negative width, we discard the second solution. So the width is approximately 4.68 units.
Plug the value of w into the first equation to find the length:
L = 3*4.68 + 2 = 16.04 (approximately)
We should check our answers. The area of the rectangle is width times length, which should be 75:
4.68 * 16.04 = 75.1 (approximately)
The slight difference is due to the rounding. So, our solution is correct.
Consider how we approached this problem. We took the given information, translated it into mathematical equations, and then solved those equations. Recognizing that the problem was a quadratic equation allowed us to use the quadratic formula, which is a common method for solving such problems.
As you can see, with the right approach, even complex math problems can be broken down into manageable steps. This process requires practice, but over time, it will become second nature.
If you are a Class 7 CBSE student looking to practice class 7 math online for better marks, you can visit LearnTheta. It’s an online platform designed to aid you in achieving effective preparation.
For all your quant-related needs, visit LearnTheta
Leave a Comment Cancel Reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.

Designorate
Design thinking, innovation, user experience and healthcare design
The Six Systems Thinking Steps to Solve Complex Problems
A quick overview of common problem solving techniques indicates that most of these methods focus on the problem rather than the whole eco-system where the problem exists. Along with the challenges of global economy , problems turn out to be more complicated and sometimes awakening problems. Climate change, traffic problems, and organizational problems that have developed through the years are all complex problems that we shouldn’t look at the same way as simple or linear problems. Part of the problem of thinking about a complex problem is the way we approach it, which may contribute to making the problem even more complex. As stated by Albert Einstein, “The problems cannot be solved using the same level of thinking that created them.” Systems thinking tends to focus on the broader ecosystem rather than the problem itself.
Systems thinking was developed by Jay Forrester and members of the Society for Organizational Learning at MIT. The idea is described in his book, The Fifth Discipline , as follows: “Systems thinking is a discipline for seeing wholes. It is a framework for seeing interrelationships rather than things, for seeing patterns of change rather than static ‘snapshots.’” A common example of the systems thinking method is the life around us where multiple systems interact with each other and are affected by each other. This wide perspective of systems thinking promotes it to solve complex problems that are dependent on external factors. Below are some of the stations that system thinking may contribute to solve.
- Complex problems that involve different factors, which require understanding the big picture in order to be efficiently solved
- Situations that are affecting, are being affected by, or affect the surrounding systems
- Problems that have turned more complicated by previous attempts to solve them
Concepts of Systems Thinking
In order to understand systems thinking, a number of concepts should be highlighted in order to define the relation between the problem and the other elements in the system and how to observe this relation in order to reach an effective solution. These principles include the following.
- All systems are composed of interconnected parts, and changing one part affects the entire system, including other parts.
- The structure of a system determines its behavior, which means that the system depends on the connection between parts rather that the part themselves.
- System behavior is an emergent phenomenon. System behavior is hard to predict due its continuously changing, non-linear relations and its time delay. It can’t be predicted by simply inspecting its elements or structure.
- Feedback loops control a system’s major dynamic behavior. The feedback loop is a number of connections causing an output from one part to eventually influence input to that same part. The number of feedback loops are larger than the system parts, which contributes to increasing system complicity.
- Complex social systems exhibit counterintuitive behavior. Solving complex problems can’t be achieved through everyday problem solving methods. They can be solved only through analytical methods and tools. Solving complex problems can be achieved through systems thinking, a process that fits the problem, and system dynamics , which is an approach to model systems by emphasizing their feedback loops.
Systems Thinking in Six Steps
In their paper Six Steps to Thinking Systemically , Michael Goodman and Richard Karash introduced six steps to apply systems thinking principles while solving complex problems. These steps were part of their case study to Bijou Bottling company’s problem of getting their orders shipped on time.
Set 1: Tell the Story
The first step in solving the problem is to understand it, and this can be achieved through looking deeply at the whole system rather than individual parts. This step requires meeting with the stakeholders to share their vision about the situation. One of the common tools to build this understanding is to utilize Concept Maps, which are graphical tools used to represent the organization or a structure of knowledge. Concept Maps visually present the system’s elements, concept links, proposition statements, cross-links, and examples.
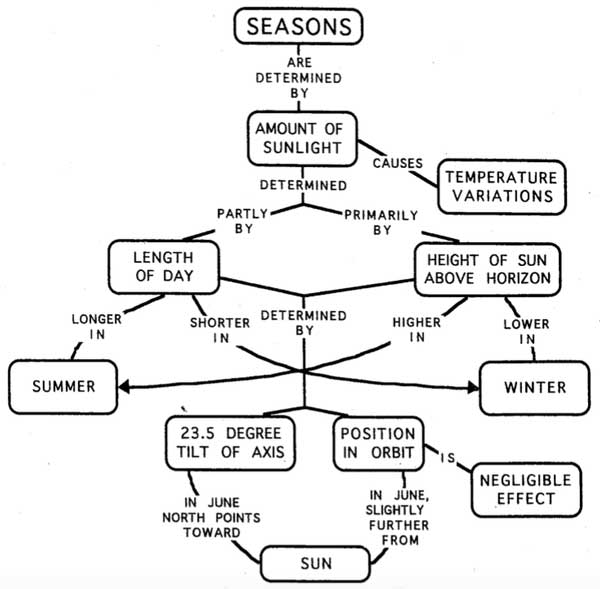
Step 2: Draw Behavior Over Time (BOT) Graphs
When thinking about a problem, we are influenced with the current situation that is reflected in our analysis, yet the problem follows a time dimension, which means that it should be tracked through the time. The Behavior Over Time graph draws a curve that presents a specific behavior (Y) through the time (X). This graph helps us to understanding whether or not the current solution is effective.
Step 3: Create a Focusing Statement
At this point, there should be a clear vision about the problem solving process, which is defined in the from of a statement that indicates the team’s target and why the problem occurs.
Step 4: Identify the Structure
After having clear vision about the problem through the proposed statement, the system structure should be described, including the behavior patterns. Building these patterns helps in understanding more about the problem, and it can be formed as a system archetype.
Step 5: Going Deeper into the Issues
After defining the problem and the system structure, this step tends to understand the underlying problems through clarifying four items: the purpose of the system (what we want), the mental models, the large system, and personal role in the situation.
Set 6: Plan an Intervention
The previously collected information is used to start the intervention phase, where modifications to the current problem relate parts to connections. This intervention attempts to reach the desirable behavior.
Practice Example of Systems Thinking
One of the direct examples of adopting the systems thinking method was presented by Daniel Aronson highlighting insects who caused damage crops. Traditional thinking to solve crop damage is to apply more pesticides to reduce the number of insects and subsequently reduce the crop damage. However, this solution solves the problem for a short term. In the long run, the problem isn’t truly solved, as the original insect eating the crops are controlling the population of another species of insect in the environment either by preying on it or competing with it. Subsequently, the crop damage increases again due to the increasing numbers of other insect species.
Observing the ecosystem that includes both the insects and the crops, systems thinking suggests exploring a solution that ensures reducing the crop damage in the long run without affecting the environmental balance, such as deploying the Integrated Pest Management that has proven success based on MIT and the National Academy of Science. This solution tends to control the number of an insect species by introducing its predators in the area.
Unlike everyday problems, complex problems can’t be solved using traditional problem solving methods due to the nature of the problems and their complexity. One of the theories that attempts to understand complex problems is systems thinking, which is defined by a number of characters. Six steps are to be used to explore and solve complex problems under the umbrella of systems thinking, which help us to observe and think in a whole eco-system rather than individual parts. Systems thinking can be deployed in multiple domains to solve organization problem, or global problems such as energy, pollution, and poverty.
Wait, Join my Newsletters!
As always, I try to come to you with design ideas, tips, and tools for design and creative thinking. Subscribe to my newsletters to receive new updated design tools and tips!
Dr Rafiq Elmansy
As an academic and author, I've had the privilege of shaping the design landscape. I teach design at the University of Leeds and am the Programme Leader for the MA Design, focusing on design thinking, design for health, and behavioural design. I've developed and taught several innovative programmes at Wrexham Glyndwr University, Northumbria University, and The American University in Cairo. I'm also a published book author and the proud founder of Designorate.com, a platform that has been instrumental in fostering design innovation. My expertise in design has been recognised by prestigious organizations. I'm a fellow of the Higher Education Academy (HEA), the Design Research Society (FDRS), and an Adobe Education Leader. Over the course of 20 years, I've had the privilege of working with esteemed clients such as the UN, World Bank, Adobe, and Schneider, contributing to their design strategies. For more than 12 years, I collaborated closely with the Adobe team, playing a key role in the development of many Adobe applications.
You May Also Like

How Does Apple’s Design Process Work?

6 Steps for Effective Critical Thinking

Using the MPPF Method in the Double Diamond Design Process

Five Steps to Achieve a Reliable Decision-Making Process

Measuring Design Thinking Impact

What is the 8D Problem Solving? And How to use the 8D Report?
3 thoughts on “ the six systems thinking steps to solve complex problems ”.
“Systems thinking was developed by Jay Forrester and members of the Society for Organizational Learning at MIT. The idea is described in his book, The Fifth Discipline, as follows:” Peter Senge is the author of The Fifth Discipline
Thank you so much Misi for the helpful information.
Thank you for the valuable information. I believe that systems thinking can be applied to every aspect of our lives. When you teach yourself to spot patterns, cycles, and loops instead of individuals elements. You see behind the scenes. Understand what actually needs addressing to move forward and make progress faster with less damage.
Leave a Reply Cancel reply
Your email address will not be published. Required fields are marked *
Sign me up for the newsletter!
- Courses for Individuals
Understanding and Solving Complex Business Problems
| Course Dates | Format | Location | Duration | Time Commitment | Price | In Person | Cambridge, MA | 2 days | 8 hours/day | $4,500 |
|---|---|---|---|---|---|
| Dec 12-13, 2024 | Live Online | N/A | 2 days | 8 hours/day | $4,500 |
Management and Leadership
Certificate Credits
- Operations
- Systems Thinking
- Participants
Course Highlights
- Discover MIT's unique, powerful, and integrative System Dynamics approach to assess problems that will not go away
- Experience the Beer Game, which simulates the supply chain of the beer industry
- Learn a new way of thinking about and resolving complex, persistent problems that emerge from change
- Earn a certificate of course completion from the MIT Sloan School of Management
Why attend Understanding and Solving Complex Business Problems?
Systems thinking was designed to improve people's ability to manage organizations comprehensively in a volatile global environment. It offers managers a framework for understanding complex situations and the dynamics those situations produce. Systems thinking is a response to the rapid changes in technology, population, and economic activity that are transforming the world, and as a way to deal with the ever-increasing complexity of today's business.
Senior managers can use systems thinking to design policies that lead their organizations to high performance. The program is intended to give participants the tools and confidence to manage organizations with full understanding and solid strategy.
Course experience
This complex problem-solving course introduces participants to MIT's unique, powerful, and integrative System Dynamics approach to assess problems that will not go away and to produce the results they want. Through exercises and simulation models, participants experience the long-term side effects and impacts of decisions and understand the ways in which performance is tied to structures and policies.
Sample Schedule—Subject to Change
This program is designed for executives with decision-making responsibility who are looking for fresh ideas to resolve organizational problems.
Past participants have included
- VPs and EVPs
- Corporate planners and strategists
- Senior Project Managers
- Product Development Managers

Request Course Information
Receive email updates related to this course, including faculty news and additional offering dates.
Review our Privacy Policy.
This program is designed to empower you to analyze complex problems in any area by using powerful yet very simple tools which are also very easy to use in real world, I enjoyed it a lot.
—Jia X.
Enroll Now!
What mit’s beer game teaches about panic hoarding, mit’s ‘beer game’ shows humans are weakest link in supply chains, the beer game, john sterman on system dynamics, how the ‘beer game’ helps retailers solve toilet paper crisis, course offerings.
An official website of the United States government
The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site.
The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely.
- Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now .
- Advanced Search
- Journal List
- Front Psychol
Complex Problem Solving: What It Is and What It Is Not
Dietrich dörner.
1 Department of Psychology, University of Bamberg, Bamberg, Germany
Joachim Funke
2 Department of Psychology, Heidelberg University, Heidelberg, Germany
Computer-simulated scenarios have been part of psychological research on problem solving for more than 40 years. The shift in emphasis from simple toy problems to complex, more real-life oriented problems has been accompanied by discussions about the best ways to assess the process of solving complex problems. Psychometric issues such as reliable assessments and addressing correlations with other instruments have been in the foreground of these discussions and have left the content validity of complex problem solving in the background. In this paper, we return the focus to content issues and address the important features that define complex problems.
Succeeding in the 21st century requires many competencies, including creativity, life-long learning, and collaboration skills (e.g., National Research Council, 2011 ; Griffin and Care, 2015 ), to name only a few. One competence that seems to be of central importance is the ability to solve complex problems ( Mainzer, 2009 ). Mainzer quotes the Nobel prize winner Simon (1957) who wrote as early as 1957:
The capacity of the human mind for formulating and solving complex problems is very small compared with the size of the problem whose solution is required for objectively rational behavior in the real world or even for a reasonable approximation to such objective rationality. (p. 198)
The shift from well-defined to ill-defined problems came about as a result of a disillusion with the “general problem solver” ( Newell et al., 1959 ): The general problem solver was a computer software intended to solve all kind of problems that can be expressed through well-formed formulas. However, it soon became clear that this procedure was in fact a “special problem solver” that could only solve well-defined problems in a closed space. But real-world problems feature open boundaries and have no well-determined solution. In fact, the world is full of wicked problems and clumsy solutions ( Verweij and Thompson, 2006 ). As a result, solving well-defined problems and solving ill-defined problems requires different cognitive processes ( Schraw et al., 1995 ; but see Funke, 2010 ).
Well-defined problems have a clear set of means for reaching a precisely described goal state. For example: in a match-stick arithmetic problem, a person receives a false arithmetic expression constructed out of matchsticks (e.g., IV = III + III). According to the instructions, moving one of the matchsticks will make the equations true. Here, both the problem (find the appropriate stick to move) and the goal state (true arithmetic expression; solution is: VI = III + III) are defined clearly.
Ill-defined problems have no clear problem definition, their goal state is not defined clearly, and the means of moving towards the (diffusely described) goal state are not clear. For example: The goal state for solving the political conflict in the near-east conflict between Israel and Palestine is not clearly defined (living in peaceful harmony with each other?) and even if the conflict parties would agree on a two-state solution, this goal again leaves many issues unresolved. This type of problem is called a “complex problem” and is of central importance to this paper. All psychological processes that occur within individual persons and deal with the handling of such ill-defined complex problems will be subsumed under the umbrella term “complex problem solving” (CPS).
Systematic research on CPS started in the 1970s with observations of the behavior of participants who were confronted with computer simulated microworlds. For example, in one of those microworlds participants assumed the role of executives who were tasked to manage a company over a certain period of time (see Brehmer and Dörner, 1993 , for a discussion of this methodology). Today, CPS is an established concept and has even influenced large-scale assessments such as PISA (“Programme for International Student Assessment”), organized by the Organization for Economic Cooperation and Development ( OECD, 2014 ). According to the World Economic Forum, CPS is one of the most important competencies required in the future ( World Economic Forum, 2015 ). Numerous articles on the subject have been published in recent years, documenting the increasing research activity relating to this field. In the following collection of papers we list only those published in 2010 and later: theoretical papers ( Blech and Funke, 2010 ; Funke, 2010 ; Knauff and Wolf, 2010 ; Leutner et al., 2012 ; Selten et al., 2012 ; Wüstenberg et al., 2012 ; Greiff et al., 2013b ; Fischer and Neubert, 2015 ; Schoppek and Fischer, 2015 ), papers about measurement issues ( Danner et al., 2011a ; Greiff et al., 2012 , 2015a ; Alison et al., 2013 ; Gobert et al., 2015 ; Greiff and Fischer, 2013 ; Herde et al., 2016 ; Stadler et al., 2016 ), papers about applications ( Fischer and Neubert, 2015 ; Ederer et al., 2016 ; Tremblay et al., 2017 ), papers about differential effects ( Barth and Funke, 2010 ; Danner et al., 2011b ; Beckmann and Goode, 2014 ; Greiff and Neubert, 2014 ; Scherer et al., 2015 ; Meißner et al., 2016 ; Wüstenberg et al., 2016 ), one paper about developmental effects ( Frischkorn et al., 2014 ), one paper with a neuroscience background ( Osman, 2012 ) 1 , papers about cultural differences ( Güss and Dörner, 2011 ; Sonnleitner et al., 2014 ; Güss et al., 2015 ), papers about validity issues ( Goode and Beckmann, 2010 ; Greiff et al., 2013c ; Schweizer et al., 2013 ; Mainert et al., 2015 ; Funke et al., 2017 ; Greiff et al., 2017 , 2015b ; Kretzschmar et al., 2016 ; Kretzschmar, 2017 ), review papers and meta-analyses ( Osman, 2010 ; Stadler et al., 2015 ), and finally books ( Qudrat-Ullah, 2015 ; Csapó and Funke, 2017b ) and book chapters ( Funke, 2012 ; Hotaling et al., 2015 ; Funke and Greiff, 2017 ; Greiff and Funke, 2017 ; Csapó and Funke, 2017a ; Fischer et al., 2017 ; Molnàr et al., 2017 ; Tobinski and Fritz, 2017 ; Viehrig et al., 2017 ). In addition, a new “Journal of Dynamic Decision Making” (JDDM) has been launched ( Fischer et al., 2015 , 2016 ) to give the field an open-access outlet for research and discussion.
This paper aims to clarify aspects of validity: what should be meant by the term CPS and what not? This clarification seems necessary because misunderstandings in recent publications provide – from our point of view – a potentially misleading picture of the construct. We start this article with a historical review before attempting to systematize different positions. We conclude with a working definition.
Historical Review
The concept behind CPS goes back to the German phrase “komplexes Problemlösen” (CPS; the term “komplexes Problemlösen” was used as a book title by Funke, 1986 ). The concept was introduced in Germany by Dörner and colleagues in the mid-1970s (see Dörner et al., 1975 ; Dörner, 1975 ) for the first time. The German phrase was later translated to CPS in the titles of two edited volumes by Sternberg and Frensch (1991) and Frensch and Funke (1995a) that collected papers from different research traditions. Even though it looks as though the term was coined in the 1970s, Edwards (1962) used the term “dynamic decision making” to describe decisions that come in a sequence. He compared static with dynamic decision making, writing:
- simple In dynamic situations, a new complication not found in the static situations arises. The environment in which the decision is set may be changing, either as a function of the sequence of decisions, or independently of them, or both. It is this possibility of an environment which changes while you collect information about it which makes the task of dynamic decision theory so difficult and so much fun. (p. 60)
The ability to solve complex problems is typically measured via dynamic systems that contain several interrelated variables that participants need to alter. Early work (see, e.g., Dörner, 1980 ) used a simulation scenario called “Lohhausen” that contained more than 2000 variables that represented the activities of a small town: Participants had to take over the role of a mayor for a simulated period of 10 years. The simulation condensed these ten years to ten hours in real time. Later, researchers used smaller dynamic systems as scenarios either based on linear equations (see, e.g., Funke, 1993 ) or on finite state automata (see, e.g., Buchner and Funke, 1993 ). In these contexts, CPS consisted of the identification and control of dynamic task environments that were previously unknown to the participants. Different task environments came along with different degrees of fidelity ( Gray, 2002 ).
According to Funke (2012) , the typical attributes of complex systems are (a) complexity of the problem situation which is usually represented by the sheer number of involved variables; (b) connectivity and mutual dependencies between involved variables; (c) dynamics of the situation, which reflects the role of time and developments within a system; (d) intransparency (in part or full) about the involved variables and their current values; and (e) polytely (greek term for “many goals”), representing goal conflicts on different levels of analysis. This mixture of features is similar to what is called VUCA (volatility, uncertainty, complexity, ambiguity) in modern approaches to management (e.g., Mack et al., 2016 ).
In his evaluation of the CPS movement, Sternberg (1995) compared (young) European approaches to CPS with (older) American research on expertise. His analysis of the differences between the European and American traditions shows advantages but also potential drawbacks for each side. He states (p. 301): “I believe that although there are problems with the European approach, it deals with some fundamental questions that American research scarcely addresses.” So, even though the echo of the European approach did not enjoy strong resonance in the US at that time, it was valued by scholars like Sternberg and others. Before attending to validity issues, we will first present a short review of different streams.
Different Approaches to CPS
In the short history of CPS research, different approaches can be identified ( Buchner, 1995 ; Fischer et al., 2017 ). To systematize, we differentiate between the following five lines of research:
- simple (a) The search for individual differences comprises studies identifying interindividual differences that affect the ability to solve complex problems. This line of research is reflected, for example, in the early work by Dörner et al. (1983) and their “Lohhausen” study. Here, naïve student participants took over the role of the mayor of a small simulated town named Lohhausen for a simulation period of ten years. According to the results of the authors, it is not intelligence (as measured by conventional IQ tests) that predicts performance, but it is the ability to stay calm in the face of a challenging situation and the ability to switch easily between an analytic mode of processing and a more holistic one.
- simple (b) The search for cognitive processes deals with the processes behind understanding complex dynamic systems. Representative of this line of research is, for example, Berry and Broadbent’s (1984) work on implicit and explicit learning processes when people interact with a dynamic system called “Sugar Production”. They found that those who perform best in controlling a dynamic system can do so implicitly, without explicit knowledge of details regarding the systems’ relations.
- simple (c) The search for system factors seeks to identify the aspects of dynamic systems that determine the difficulty of complex problems and make some problems harder than others. Representative of this line of research is, for example, work by Funke (1985) , who systematically varied the number of causal effects within a dynamic system or the presence/absence of eigendynamics. He found, for example, that solution quality decreases as the number of systems relations increases.
- simple (d) The psychometric approach develops measurement instruments that can be used as an alternative to classical IQ tests, as something that goes “beyond IQ”. The MicroDYN approach ( Wüstenberg et al., 2012 ) is representative for this line of research that presents an alternative to reasoning tests (like Raven matrices). These authors demonstrated that a small improvement in predicting school grade point average beyond reasoning is possible with MicroDYN tests.
- simple (e) The experimental approach explores CPS under different experimental conditions. This approach uses CPS assessment instruments to test hypotheses derived from psychological theories and is sometimes used in research about cognitive processes (see above). Exemplary for this line of research is the work by Rohe et al. (2016) , who test the usefulness of “motto goals” in the context of complex problems compared to more traditional learning and performance goals. Motto goals differ from pure performance goals by activating positive affect and should lead to better goal attainment especially in complex situations (the mentioned study found no effect).
To be clear: these five approaches are not mutually exclusive and do overlap. But the differentiation helps to identify different research communities and different traditions. These communities had different opinions about scaling complexity.
The Race for Complexity: Use of More and More Complex Systems
In the early years of CPS research, microworlds started with systems containing about 20 variables (“Tailorshop”), soon reached 60 variables (“Moro”), and culminated in systems with about 2000 variables (“Lohhausen”). This race for complexity ended with the introduction of the concept of “minimal complex systems” (MCS; Greiff and Funke, 2009 ; Funke and Greiff, 2017 ), which ushered in a search for the lower bound of complexity instead of the higher bound, which could not be defined as easily. The idea behind this concept was that whereas the upper limits of complexity are unbound, the lower limits might be identifiable. Imagine starting with a simple system containing two variables with a simple linear connection between them; then, step by step, increase the number of variables and/or the type of connections. One soon reaches a point where the system can no longer be considered simple and has become a “complex system”. This point represents a minimal complex system. Despite some research having been conducted in this direction, the point of transition from simple to complex has not been identified clearly as of yet.
Some years later, the original “minimal complex systems” approach ( Greiff and Funke, 2009 ) shifted to the “multiple complex systems” approach ( Greiff et al., 2013a ). This shift is more than a slight change in wording: it is important because it taps into the issue of validity directly. Minimal complex systems have been introduced in the context of challenges from large-scale assessments like PISA 2012 that measure new aspects of problem solving, namely interactive problems besides static problem solving ( Greiff and Funke, 2017 ). PISA 2012 required test developers to remain within testing time constraints (given by the school class schedule). Also, test developers needed a large item pool for the construction of a broad class of problem solving items. It was clear from the beginning that MCS deal with simple dynamic situations that require controlled interaction: the exploration and control of simple ticket machines, simple mobile phones, or simple MP3 players (all of these example domains were developed within PISA 2012) – rather than really complex situations like managerial or political decision making.
As a consequence of this subtle but important shift in interpreting the letters MCS, the definition of CPS became a subject of debate recently ( Funke, 2014a ; Greiff and Martin, 2014 ; Funke et al., 2017 ). In the words of Funke (2014b , p. 495):
- simple It is funny that problems that nowadays come under the term ‘CPS’, are less complex (in terms of the previously described attributes of complex situations) than at the beginning of this new research tradition. The emphasis on psychometric qualities has led to a loss of variety. Systems thinking requires more than analyzing models with two or three linear equations – nonlinearity, cyclicity, rebound effects, etc. are inherent features of complex problems and should show up at least in some of the problems used for research and assessment purposes. Minimal complex systems run the danger of becoming minimal valid systems.
Searching for minimal complex systems is not the same as gaining insight into the way how humans deal with complexity and uncertainty. For psychometric purposes, it is appropriate to reduce complexity to a minimum; for understanding problem solving under conditions of overload, intransparency, and dynamics, it is necessary to realize those attributes with reasonable strength. This aspect is illustrated in the next section.
Importance of the Validity Issue
The most important reason for discussing the question of what complex problem solving is and what it is not stems from its phenomenology: if we lose sight of our phenomena, we are no longer doing good psychology. The relevant phenomena in the context of complex problems encompass many important aspects. In this section, we discuss four phenomena that are specific to complex problems. We consider these phenomena as critical for theory development and for the construction of assessment instruments (i.e., microworlds). These phenomena require theories for explaining them and they require assessment instruments eliciting them in a reliable way.
The first phenomenon is the emergency reaction of the intellectual system ( Dörner, 1980 ): When dealing with complex systems, actors tend to (a) reduce their intellectual level by decreasing self-reflections, by decreasing their intentions, by stereotyping, and by reducing their realization of intentions, (b) they show a tendency for fast action with increased readiness for risk, with increased violations of rules, and with increased tendency to escape the situation, and (c) they degenerate their hypotheses formation by construction of more global hypotheses and reduced tests of hypotheses, by increasing entrenchment, and by decontextualizing their goals. This phenomenon illustrates the strong connection between cognition, emotion, and motivation that has been emphasized by Dörner (see, e.g., Dörner and Güss, 2013 ) from the beginning of his research tradition; the emergency reaction reveals a shift in the mode of information processing under the pressure of complexity.
The second phenomenon comprises cross-cultural differences with respect to strategy use ( Strohschneider and Güss, 1999 ; Güss and Wiley, 2007 ; Güss et al., 2015 ). Results from complex task environments illustrate the strong influence of context and background knowledge to an extent that cannot be found for knowledge-poor problems. For example, in a comparison between Brazilian and German participants, it turned out that Brazilians accept the given problem descriptions and are more optimistic about the results of their efforts, whereas Germans tend to inquire more about the background of the problems and take a more active approach but are less optimistic (according to Strohschneider and Güss, 1998 , p. 695).
The third phenomenon relates to failures that occur during the planning and acting stages ( Jansson, 1994 ; Ramnarayan et al., 1997 ), illustrating that rational procedures seem to be unlikely to be used in complex situations. The potential for failures ( Dörner, 1996 ) rises with the complexity of the problem. Jansson (1994) presents seven major areas for failures with complex situations: acting directly on current feedback; insufficient systematization; insufficient control of hypotheses and strategies; lack of self-reflection; selective information gathering; selective decision making; and thematic vagabonding.
The fourth phenomenon describes (a lack of) training and transfer effects ( Kretzschmar and Süß, 2015 ), which again illustrates the context dependency of strategies and knowledge (i.e., there is no strategy that is so universal that it can be used in many different problem situations). In their own experiment, the authors could show training effects only for knowledge acquisition, not for knowledge application. Only with specific feedback, performance in complex environments can be increased ( Engelhart et al., 2017 ).
These four phenomena illustrate why the type of complexity (or degree of simplicity) used in research really matters. Furthermore, they demonstrate effects that are specific for complex problems, but not for toy problems. These phenomena direct the attention to the important question: does the stimulus material used (i.e., the computer-simulated microworld) tap and elicit the manifold of phenomena described above?
Dealing with partly unknown complex systems requires courage, wisdom, knowledge, grit, and creativity. In creativity research, “little c” and “BIG C” are used to differentiate between everyday creativity and eminent creativity ( Beghetto and Kaufman, 2007 ; Kaufman and Beghetto, 2009 ). Everyday creativity is important for solving everyday problems (e.g., finding a clever fix for a broken spoke on my bicycle), eminent creativity changes the world (e.g., inventing solar cells for energy production). Maybe problem solving research should use a similar differentiation between “little p” and “BIG P” to mark toy problems on the one side and big societal challenges on the other. The question then remains: what can we learn about BIG P by studying little p? What phenomena are present in both types, and what phenomena are unique to each of the two extremes?
Discussing research on CPS requires reflecting on the field’s research methods. Even if the experimental approach has been successful for testing hypotheses (for an overview of older work, see Funke, 1995 ), other methods might provide additional and novel insights. Complex phenomena require complex approaches to understand them. The complex nature of complex systems imposes limitations on psychological experiments: The more complex the environments, the more difficult is it to keep conditions under experimental control. And if experiments have to be run in labs one should bring enough complexity into the lab to establish the phenomena mentioned, at least in part.
There are interesting options to be explored (again): think-aloud protocols , which have been discredited for many years ( Nisbett and Wilson, 1977 ) and yet are a valuable source for theory testing ( Ericsson and Simon, 1983 ); introspection ( Jäkel and Schreiber, 2013 ), which seems to be banned from psychological methods but nevertheless offers insights into thought processes; the use of life-streaming ( Wendt, 2017 ), a medium in which streamers generate a video stream of think-aloud data in computer-gaming; political decision-making ( Dhami et al., 2015 ) that demonstrates error-proneness in groups; historical case studies ( Dörner and Güss, 2011 ) that give insights into the thinking styles of political leaders; the use of the critical incident technique ( Reuschenbach, 2008 ) to construct complex scenarios; and simulations with different degrees of fidelity ( Gray, 2002 ).
The methods tool box is full of instruments that have to be explored more carefully before any individual instrument receives a ban or research narrows its focus to only one paradigm for data collection. Brehmer and Dörner (1993) discussed the tensions between “research in the laboratory and research in the field”, optimistically concluding “that the new methodology of computer-simulated microworlds will provide us with the means to bridge the gap between the laboratory and the field” (p. 183). The idea behind this optimism was that computer-simulated scenarios would bring more complexity from the outside world into the controlled lab environment. But this is not true for all simulated scenarios. In his paper on simulated environments, Gray (2002) differentiated computer-simulated environments with respect to three dimensions: (1) tractability (“the more training subjects require before they can use a simulated task environment, the less tractable it is”, p. 211), correspondence (“High correspondence simulated task environments simulate many aspects of one task environment. Low correspondence simulated task environments simulate one aspect of many task environments”, p. 214), and engagement (“A simulated task environment is engaging to the degree to which it involves and occupies the participants; that is, the degree to which they agree to take it seriously”, p. 217). But the mere fact that a task is called a “computer-simulated task environment” does not mean anything specific in terms of these three dimensions. This is one of several reasons why we should differentiate between those studies that do not address the core features of CPS and those that do.
What is not CPS?
Even though a growing number of references claiming to deal with complex problems exist (e.g., Greiff and Wüstenberg, 2015 ; Greiff et al., 2016 ), it would be better to label the requirements within these tasks “dynamic problem solving,” as it has been done adequately in earlier work ( Greiff et al., 2012 ). The dynamics behind on-off-switches ( Thimbleby, 2007 ) are remarkable but not really complex. Small nonlinear systems that exhibit stunningly complex and unstable behavior do exist – but they are not used in psychometric assessments of so-called CPS. There are other small systems (like MicroDYN scenarios: Greiff and Wüstenberg, 2014 ) that exhibit simple forms of system behavior that are completely predictable and stable. This type of simple systems is used frequently. It is even offered commercially as a complex problem-solving test called COMPRO ( Greiff and Wüstenberg, 2015 ) for business applications. But a closer look reveals that the label is not used correctly; within COMPRO, the used linear equations are far from being complex and the system can be handled properly by using only one strategy (see for more details Funke et al., 2017 ).
Why do simple linear systems not fall within CPS? At the surface, nonlinear and linear systems might appear similar because both only include 3–5 variables. But the difference is in terms of systems behavior as well as strategies and learning. If the behavior is simple (as in linear systems where more input is related to more output and vice versa), the system can be easily understood (participants in the MicroDYN world have 3 minutes to explore a complex system). If the behavior is complex (as in systems that contain strange attractors or negative feedback loops), things become more complicated and much more observation is needed to identify the hidden structure of the unknown system ( Berry and Broadbent, 1984 ; Hundertmark et al., 2015 ).
Another issue is learning. If tasks can be solved using a single (and not so complicated) strategy, steep learning curves are to be expected. The shift from problem solving to learned routine behavior occurs rapidly, as was demonstrated by Luchins (1942) . In his water jar experiments, participants quickly acquired a specific strategy (a mental set) for solving certain measurement problems that they later continued applying to problems that would have allowed for easier approaches. In the case of complex systems, learning can occur only on very general, abstract levels because it is difficult for human observers to make specific predictions. Routines dealing with complex systems are quite different from routines relating to linear systems.
What should not be studied under the label of CPS are pure learning effects, multiple-cue probability learning, or tasks that can be solved using a single strategy. This last issue is a problem for MicroDYN tasks that rely strongly on the VOTAT strategy (“vary one thing at a time”; see Tschirgi, 1980 ). In real-life, it is hard to imagine a business manager trying to solve her or his problems by means of VOTAT.
What is CPS?
In the early days of CPS research, planet Earth’s dynamics and complexities gained attention through such books as “The limits to growth” ( Meadows et al., 1972 ) and “Beyond the limits” ( Meadows et al., 1992 ). In the current decade, for example, the World Economic Forum (2016) attempts to identify the complexities and risks of our modern world. In order to understand the meaning of complexity and uncertainty, taking a look at the worlds’ most pressing issues is helpful. Searching for strategies to cope with these problems is a difficult task: surely there is no place for the simple principle of “vary-one-thing-at-a-time” (VOTAT) when it comes to global problems. The VOTAT strategy is helpful in the context of simple problems ( Wüstenberg et al., 2014 ); therefore, whether or not VOTAT is helpful in a given problem situation helps us distinguish simple from complex problems.
Because there exist no clear-cut strategies for complex problems, typical failures occur when dealing with uncertainty ( Dörner, 1996 ; Güss et al., 2015 ). Ramnarayan et al. (1997) put together a list of generic errors (e.g., not developing adequate action plans; lack of background control; learning from experience blocked by stereotype knowledge; reactive instead of proactive action) that are typical of knowledge-rich complex systems but cannot be found in simple problems.
Complex problem solving is not a one-dimensional, low-level construct. On the contrary, CPS is a multi-dimensional bundle of competencies existing at a high level of abstraction, similar to intelligence (but going beyond IQ). As Funke et al. (2018) state: “Assessment of transversal (in educational contexts: cross-curricular) competencies cannot be done with one or two types of assessment. The plurality of skills and competencies requires a plurality of assessment instruments.”
There are at least three different aspects of complex systems that are part of our understanding of a complex system: (1) a complex system can be described at different levels of abstraction; (2) a complex system develops over time, has a history, a current state, and a (potentially unpredictable) future; (3) a complex system is knowledge-rich and activates a large semantic network, together with a broad list of potential strategies (domain-specific as well as domain-general).
Complex problem solving is not only a cognitive process but is also an emotional one ( Spering et al., 2005 ; Barth and Funke, 2010 ) and strongly dependent on motivation (low-stakes versus high-stakes testing; see Hermes and Stelling, 2016 ).
Furthermore, CPS is a dynamic process unfolding over time, with different phases and with more differentiation than simply knowledge acquisition and knowledge application. Ideally, the process should entail identifying problems (see Dillon, 1982 ; Lee and Cho, 2007 ), even if in experimental settings, problems are provided to participants a priori . The more complex and open a given situation, the more options can be generated (T. S. Schweizer et al., 2016 ). In closed problems, these processes do not occur in the same way.
In analogy to the difference between formative (process-oriented) and summative (result-oriented) assessment ( Wiliam and Black, 1996 ; Bennett, 2011 ), CPS should not be reduced to the mere outcome of a solution process. The process leading up to the solution, including detours and errors made along the way, might provide a more differentiated impression of a person’s problem-solving abilities and competencies than the final result of such a process. This is one of the reasons why CPS environments are not, in fact, complex intelligence tests: research on CPS is not only about the outcome of the decision process, but it is also about the problem-solving process itself.
Complex problem solving is part of our daily life: finding the right person to share one’s life with, choosing a career that not only makes money, but that also makes us happy. Of course, CPS is not restricted to personal problems – life on Earth gives us many hard nuts to crack: climate change, population growth, the threat of war, the use and distribution of natural resources. In sum, many societal challenges can be seen as complex problems. To reduce that complexity to a one-hour lab activity on a random Friday afternoon puts it out of context and does not address CPS issues.
Theories about CPS should specify which populations they apply to. Across populations, one thing to consider is prior knowledge. CPS research with experts (e.g., Dew et al., 2009 ) is quite different from problem solving research using tasks that intentionally do not require any specific prior knowledge (see, e.g., Beckmann and Goode, 2014 ).
More than 20 years ago, Frensch and Funke (1995b) defined CPS as follows:
- simple CPS occurs to overcome barriers between a given state and a desired goal state by means of behavioral and/or cognitive, multi-step activities. The given state, goal state, and barriers between given state and goal state are complex, change dynamically during problem solving, and are intransparent. The exact properties of the given state, goal state, and barriers are unknown to the solver at the outset. CPS implies the efficient interaction between a solver and the situational requirements of the task, and involves a solver’s cognitive, emotional, personal, and social abilities and knowledge. (p. 18)
The above definition is rather formal and does not account for content or relations between the simulation and the real world. In a sense, we need a new definition of CPS that addresses these issues. Based on our previous arguments, we propose the following working definition:
- simple Complex problem solving is a collection of self-regulated psychological processes and activities necessary in dynamic environments to achieve ill-defined goals that cannot be reached by routine actions. Creative combinations of knowledge and a broad set of strategies are needed. Solutions are often more bricolage than perfect or optimal. The problem-solving process combines cognitive, emotional, and motivational aspects, particularly in high-stakes situations. Complex problems usually involve knowledge-rich requirements and collaboration among different persons.
The main differences to the older definition lie in the emphasis on (a) the self-regulation of processes, (b) creativity (as opposed to routine behavior), (c) the bricolage type of solution, and (d) the role of high-stakes challenges. Our new definition incorporates some aspects that have been discussed in this review but were not reflected in the 1995 definition, which focused on attributes of complex problems like dynamics or intransparency.
This leads us to the final reflection about the role of CPS for dealing with uncertainty and complexity in real life. We will distinguish thinking from reasoning and introduce the sense of possibility as an important aspect of validity.
CPS as Combining Reasoning and Thinking in an Uncertain Reality
Leading up to the Battle of Borodino in Leo Tolstoy’s novel “War and Peace”, Prince Andrei Bolkonsky explains the concept of war to his friend Pierre. Pierre expects war to resemble a game of chess: You position the troops and attempt to defeat your opponent by moving them in different directions.
“Far from it!”, Andrei responds. “In chess, you know the knight and his moves, you know the pawn and his combat strength. While in war, a battalion is sometimes stronger than a division and sometimes weaker than a company; it all depends on circumstances that can never be known. In war, you do not know the position of your enemy; some things you might be able to observe, some things you have to divine (but that depends on your ability to do so!) and many things cannot even be guessed at. In chess, you can see all of your opponent’s possible moves. In war, that is impossible. If you decide to attack, you cannot know whether the necessary conditions are met for you to succeed. Many a time, you cannot even know whether your troops will follow your orders…”
In essence, war is characterized by a high degree of uncertainty. A good commander (or politician) can add to that what he or she sees, tentatively fill in the blanks – and not just by means of logical deduction but also by intelligently bridging missing links. A bad commander extrapolates from what he sees and thus arrives at improper conclusions.
Many languages differentiate between two modes of mentalizing; for instance, the English language distinguishes between ‘thinking’ and ‘reasoning’. Reasoning denotes acute and exact mentalizing involving logical deductions. Such deductions are usually based on evidence and counterevidence. Thinking, however, is what is required to write novels. It is the construction of an initially unknown reality. But it is not a pipe dream, an unfounded process of fabrication. Rather, thinking asks us to imagine reality (“Wirklichkeitsfantasie”). In other words, a novelist has to possess a “sense of possibility” (“Möglichkeitssinn”, Robert Musil; in German, sense of possibility is often used synonymously with imagination even though imagination is not the same as sense of possibility, for imagination also encapsulates the impossible). This sense of possibility entails knowing the whole (or several wholes) or being able to construe an unknown whole that could accommodate a known part. The whole has to align with sociological and geographical givens, with the mentality of certain peoples or groups, and with the laws of physics and chemistry. Otherwise, the entire venture is ill-founded. A sense of possibility does not aim for the moon but imagines something that might be possible but has not been considered possible or even potentially possible so far.
Thinking is a means to eliminate uncertainty. This process requires both of the modes of thinking we have discussed thus far. Economic, political, or ecological decisions require us to first consider the situation at hand. Though certain situational aspects can be known, but many cannot. In fact, von Clausewitz (1832) posits that only about 25% of the necessary information is available when a military decision needs to be made. Even then, there is no way to guarantee that whatever information is available is also correct: Even if a piece of information was completely accurate yesterday, it might no longer apply today.
Once our sense of possibility has helped grasping a situation, problem solvers need to call on their reasoning skills. Not every situation requires the same action, and we may want to act this way or another to reach this or that goal. This appears logical, but it is a logic based on constantly shifting grounds: We cannot know whether necessary conditions are met, sometimes the assumptions we have made later turn out to be incorrect, and sometimes we have to revise our assumptions or make completely new ones. It is necessary to constantly switch between our sense of possibility and our sense of reality, that is, to switch between thinking and reasoning. It is an arduous process, and some people handle it well, while others do not.
If we are to believe Tuchman’s (1984) book, “The March of Folly”, most politicians and commanders are fools. According to Tuchman, not much has changed in the 3300 years that have elapsed since the misguided Trojans decided to welcome the left-behind wooden horse into their city that would end up dismantling Troy’s defensive walls. The Trojans, too, had been warned, but decided not to heed the warning. Although Laocoön had revealed the horse’s true nature to them by attacking it with a spear, making the weapons inside the horse ring, the Trojans refused to see the forest for the trees. They did not want to listen, they wanted the war to be over, and this desire ended up shaping their perception.
The objective of psychology is to predict and explain human actions and behavior as accurately as possible. However, thinking cannot be investigated by limiting its study to neatly confined fractions of reality such as the realms of propositional logic, chess, Go tasks, the Tower of Hanoi, and so forth. Within these systems, there is little need for a sense of possibility. But a sense of possibility – the ability to divine and construe an unknown reality – is at least as important as logical reasoning skills. Not researching the sense of possibility limits the validity of psychological research. All economic and political decision making draws upon this sense of possibility. By not exploring it, psychological research dedicated to the study of thinking cannot further the understanding of politicians’ competence and the reasons that underlie political mistakes. Christopher Clark identifies European diplomats’, politicians’, and commanders’ inability to form an accurate representation of reality as a reason for the outbreak of World War I. According to Clark’s (2012) book, “The Sleepwalkers”, the politicians of the time lived in their own make-believe world, wrongfully assuming that it was the same world everyone else inhabited. If CPS research wants to make significant contributions to the world, it has to acknowledge complexity and uncertainty as important aspects of it.
For more than 40 years, CPS has been a new subject of psychological research. During this time period, the initial emphasis on analyzing how humans deal with complex, dynamic, and uncertain situations has been lost. What is subsumed under the heading of CPS in modern research has lost the original complexities of real-life problems. From our point of view, the challenges of the 21st century require a return to the origins of this research tradition. We would encourage researchers in the field of problem solving to come back to the original ideas. There is enough complexity and uncertainty in the world to be studied. Improving our understanding of how humans deal with these global and pressing problems would be a worthwhile enterprise.
Author Contributions
JF drafted a first version of the manuscript, DD added further text and commented on the draft. JF finalized the manuscript.
Authors Note
After more than 40 years of controversial discussions between both authors, this is the first joint paper. We are happy to have done this now! We have found common ground!
Conflict of Interest Statement
The authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Acknowledgments
The authors thank the Deutsche Forschungsgemeinschaft (DFG) for the continuous support of their research over many years. Thanks to Daniel Holt for his comments on validity issues, thanks to Julia Nolte who helped us by translating German text excerpts into readable English and helped us, together with Keri Hartman, to improve our style and grammar – thanks for that! We also thank the two reviewers for their helpful critical comments on earlier versions of this manuscript. Finally, we acknowledge financial support by Deutsche Forschungsgemeinschaft and Ruprecht-Karls-Universität Heidelberg within their funding programme Open Access Publishing .
1 The fMRI-paper from Anderson (2012) uses the term “complex problem solving” for tasks that do not fall in our understanding of CPS and is therefore excluded from this list.
- Alison L., van den Heuvel C., Waring S., Power N., Long A., O’Hara T., et al. (2013). Immersive simulated learning environments for researching critical incidents: a knowledge synthesis of the literature and experiences of studying high-risk strategic decision making. J. Cogn. Eng. Deci. Mak. 7 255–272. 10.1177/1555343412468113 [ CrossRef ] [ Google Scholar ]
- Anderson J. R. (2012). Tracking problem solving by multivariate pattern analysis and hidden markov model algorithms. Neuropsychologia 50 487–498. 10.1016/j.neuropsychologia.2011.07.025 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Barth C. M., Funke J. (2010). Negative affective environments improve complex solving performance. Cogn. Emot. 24 1259–1268. 10.1080/02699930903223766 [ CrossRef ] [ Google Scholar ]
- Beckmann J. F., Goode N. (2014). The benefit of being naïve and knowing it: the unfavourable impact of perceived context familiarity on learning in complex problem solving tasks. Instruct. Sci. 42 271–290. 10.1007/s11251-013-9280-7 [ CrossRef ] [ Google Scholar ]
- Beghetto R. A., Kaufman J. C. (2007). Toward a broader conception of creativity: a case for “mini-c” creativity. Psychol. Aesthetics Creat. Arts 1 73–79. 10.1037/1931-3896.1.2.73 [ CrossRef ] [ Google Scholar ]
- Bennett R. E. (2011). Formative assessment: a critical review. Assess. Educ. Princ. Policy Pract. 18 5–25. 10.1080/0969594X.2010.513678 [ CrossRef ] [ Google Scholar ]
- Berry D. C., Broadbent D. E. (1984). On the relationship between task performance and associated verbalizable knowledge. Q. J. Exp. Psychol. 36 209–231. 10.1080/14640748408402156 [ CrossRef ] [ Google Scholar ]
- Blech C., Funke J. (2010). You cannot have your cake and eat it, too: how induced goal conflicts affect complex problem solving. Open Psychol. J. 3 42–53. 10.2174/1874350101003010042 [ CrossRef ] [ Google Scholar ]
- Brehmer B., Dörner D. (1993). Experiments with computer-simulated microworlds: escaping both the narrow straits of the laboratory and the deep blue sea of the field study. Comput. Hum. Behav. 9 171–184. 10.1016/0747-5632(93)90005-D [ CrossRef ] [ Google Scholar ]
- Buchner A. (1995). “Basic topics and approaches to the study of complex problem solving,” in Complex Problem Solving: The European Perspective , eds Frensch P. A., Funke J. (Hillsdale, NJ: Erlbaum; ), 27–63. [ Google Scholar ]
- Buchner A., Funke J. (1993). Finite state automata: dynamic task environments in problem solving research. Q. J. Exp. Psychol. 46A , 83–118. 10.1080/14640749308401068 [ CrossRef ] [ Google Scholar ]
- Clark C. (2012). The Sleepwalkers: How Europe Went to War in 1914 . London: Allen Lane. [ Google Scholar ]
- Csapó B., Funke J. (2017a). “The development and assessment of problem solving in 21st-century schools,” in The Nature of Problem Solving: Using Research to Inspire 21st Century Learning , eds Csapó B., Funke J. (Paris: OECD Publishing; ), 19–31. [ Google Scholar ]
- Csapó B., Funke J. (eds) (2017b). The Nature of Problem Solving. Using Research to Inspire 21st Century Learning. Paris: OECD Publishing. [ Google Scholar ]
- Danner D., Hagemann D., Holt D. V., Hager M., Schankin A., Wüstenberg S., et al. (2011a). Measuring performance in dynamic decision making. Reliability and validity of the Tailorshop simulation. J. Ind. Differ. 32 225–233. 10.1027/1614-0001/a000055 [ CrossRef ] [ Google Scholar ]
- Danner D., Hagemann D., Schankin A., Hager M., Funke J. (2011b). Beyond IQ: a latent state-trait analysis of general intelligence, dynamic decision making, and implicit learning. Intelligence 39 323–334. 10.1016/j.intell.2011.06.004 [ CrossRef ] [ Google Scholar ]
- Dew N., Read S., Sarasvathy S. D., Wiltbank R. (2009). Effectual versus predictive logics in entrepreneurial decision-making: differences between experts and novices. J. Bus. Ventur. 24 287–309. 10.1016/j.jbusvent.2008.02.002 [ CrossRef ] [ Google Scholar ]
- Dhami M. K., Mandel D. R., Mellers B. A., Tetlock P. E. (2015). Improving intelligence analysis with decision science. Perspect. Psychol. Sci. 10 753–757. 10.1177/1745691615598511 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Dillon J. T. (1982). Problem finding and solving. J. Creat. Behav. 16 97–111. 10.1002/j.2162-6057.1982.tb00326.x [ CrossRef ] [ Google Scholar ]
- Dörner D. (1975). Wie Menschen eine Welt verbessern wollten [How people wanted to improve a world]. Bild Der Wissenschaft 12 48–53. [ Google Scholar ]
- Dörner D. (1980). On the difficulties people have in dealing with complexity. Simulat. Gam. 11 87–106. 10.1177/104687818001100108 [ CrossRef ] [ Google Scholar ]
- Dörner D. (1996). The Logic of Failure: Recognizing and Avoiding Error in Complex Situations. New York, NY: Basic Books. [ Google Scholar ]
- Dörner D., Drewes U., Reither F. (1975). “Über das Problemlösen in sehr komplexen Realitätsbereichen,” in Bericht über den 29. Kongreß der DGfPs in Salzburg 1974 Band 1 , ed. Tack W. H. (Göttingen: Hogrefe; ), 339–340. [ Google Scholar ]
- Dörner D., Güss C. D. (2011). A psychological analysis of Adolf Hitler’s decision making as commander in chief: summa confidentia et nimius metus. Rev. Gen. Psychol. 15 37–49. 10.1037/a0022375 [ CrossRef ] [ Google Scholar ]
- Dörner D., Güss C. D. (2013). PSI: a computational architecture of cognition, motivation, and emotion. Rev. Gen. Psychol. 17 297–317. 10.1037/a0032947 [ CrossRef ] [ Google Scholar ]
- Dörner D., Kreuzig H. W., Reither F., Stäudel T. (1983). Lohhausen. Vom Umgang mit Unbestimmtheit und Komplexität. Bern: Huber. [ Google Scholar ]
- Ederer P., Patt A., Greiff S. (2016). Complex problem-solving skills and innovativeness – evidence from occupational testing and regional data. Eur. J. Educ. 51 244–256. 10.1111/ejed.12176 [ CrossRef ] [ Google Scholar ]
- Edwards W. (1962). Dynamic decision theory and probabiIistic information processing. Hum. Factors 4 59–73. 10.1177/001872086200400201 [ CrossRef ] [ Google Scholar ]
- Engelhart M., Funke J., Sager S. (2017). A web-based feedback study on optimization-based training and analysis of human decision making. J. Dynamic Dec. Mak. 3 1–23. [ Google Scholar ]
- Ericsson K. A., Simon H. A. (1983). Protocol Analysis: Verbal Reports As Data. Cambridge, MA: Bradford. [ Google Scholar ]
- Fischer A., Greiff S., Funke J. (2017). “The history of complex problem solving,” in The Nature of Problem Solving: Using Research to Inspire 21st Century Learning , eds Csapó B., Funke J. (Paris: OECD Publishing; ), 107–121. [ Google Scholar ]
- Fischer A., Holt D. V., Funke J. (2015). Promoting the growing field of dynamic decision making. J. Dynamic Decis. Mak. 1 1–3. 10.11588/jddm.2015.1.23807 [ CrossRef ] [ Google Scholar ]
- Fischer A., Holt D. V., Funke J. (2016). The first year of the “journal of dynamic decision making.” J. Dynamic Decis. Mak. 2 1–2. 10.11588/jddm.2016.1.28995 [ CrossRef ] [ Google Scholar ]
- Fischer A., Neubert J. C. (2015). The multiple faces of complex problems: a model of problem solving competency and its implications for training and assessment. J. Dynamic Decis. Mak. 1 1–14. 10.11588/jddm.2015.1.23945 [ CrossRef ] [ Google Scholar ]
- Frensch P. A., Funke J. (eds) (1995a). Complex Problem Solving: The European Perspective. Hillsdale, NJ: Erlbaum. [ Google Scholar ]
- Frensch P. A., Funke J. (1995b). “Definitions, traditions, and a general framework for understanding complex problem solving,” in Complex Problem Solving: The European Perspective , eds Frensch P. A., Funke J. (Hillsdale, NJ: Lawrence Erlbaum; ), 3–25. [ Google Scholar ]
- Frischkorn G. T., Greiff S., Wüstenberg S. (2014). The development of complex problem solving in adolescence: a latent growth curve analysis. J. Educ. Psychol. 106 1004–1020. 10.1037/a0037114 [ CrossRef ] [ Google Scholar ]
- Funke J. (1985). Steuerung dynamischer Systeme durch Aufbau und Anwendung subjektiver Kausalmodelle. Z. Psychol. 193 435–457. [ Google Scholar ]
- Funke J. (1986). Komplexes Problemlösen - Bestandsaufnahme und Perspektiven [Complex Problem Solving: Survey and Perspectives]. Heidelberg: Springer. [ Google Scholar ]
- Funke J. (1993). “Microworlds based on linear equation systems: a new approach to complex problem solving and experimental results,” in The Cognitive Psychology of Knowledge , eds Strube G., Wender K.-F. (Amsterdam: Elsevier Science Publishers; ), 313–330. [ Google Scholar ]
- Funke J. (1995). “Experimental research on complex problem solving,” in Complex Problem Solving: The European Perspective , eds Frensch P. A., Funke J. (Hillsdale, NJ: Erlbaum; ), 243–268. [ Google Scholar ]
- Funke J. (2010). Complex problem solving: a case for complex cognition? Cogn. Process. 11 133–142. 10.1007/s10339-009-0345-0 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Funke J. (2012). “Complex problem solving,” in Encyclopedia of the Sciences of Learning Vol. 38 ed. Seel N. M. (Heidelberg: Springer; ), 682–685. [ Google Scholar ]
- Funke J. (2014a). Analysis of minimal complex systems and complex problem solving require different forms of causal cognition. Front. Psychol. 5 : 739 10.3389/fpsyg.2014.00739 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Funke J. (2014b). “Problem solving: what are the important questions?,” in Proceedings of the 36th Annual Conference of the Cognitive Science Society , eds Bello P., Guarini M., McShane M., Scassellati B. (Austin, TX: Cognitive Science Society; ), 493–498. [ Google Scholar ]
- Funke J., Fischer A., Holt D. V. (2017). When less is less: solving multiple simple problems is not complex problem solving—A comment on Greiff et al. (2015). J. Intell. 5 : 5 10.3390/jintelligence5010005 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Funke J., Fischer A., Holt D. V. (2018). “Competencies for complexity: problem solving in the 21st century,” in Assessment and Teaching of 21st Century Skills , eds Care E., Griffin P., Wilson M. (Dordrecht: Springer; ), 3. [ Google Scholar ]
- Funke J., Greiff S. (2017). “Dynamic problem solving: multiple-item testing based on minimally complex systems,” in Competence Assessment in Education. Research, Models and Instruments , eds Leutner D., Fleischer J., Grünkorn J., Klieme E. (Heidelberg: Springer; ), 427–443. [ Google Scholar ]
- Gobert J. D., Kim Y. J., Pedro M. A. S., Kennedy M., Betts C. G. (2015). Using educational data mining to assess students’ skills at designing and conducting experiments within a complex systems microworld. Think. Skills Creat. 18 81–90. 10.1016/j.tsc.2015.04.008 [ CrossRef ] [ Google Scholar ]
- Goode N., Beckmann J. F. (2010). You need to know: there is a causal relationship between structural knowledge and control performance in complex problem solving tasks. Intelligence 38 345–352. 10.1016/j.intell.2010.01.001 [ CrossRef ] [ Google Scholar ]
- Gray W. D. (2002). Simulated task environments: the role of high-fidelity simulations, scaled worlds, synthetic environments, and laboratory tasks in basic and applied cognitive research. Cogn. Sci. Q. 2 205–227. [ Google Scholar ]
- Greiff S., Fischer A. (2013). Measuring complex problem solving: an educational application of psychological theories. J. Educ. Res. 5 38–58. [ Google Scholar ]
- Greiff S., Fischer A., Stadler M., Wüstenberg S. (2015a). Assessing complex problem-solving skills with multiple complex systems. Think. Reason. 21 356–382. 10.1080/13546783.2014.989263 [ CrossRef ] [ Google Scholar ]
- Greiff S., Stadler M., Sonnleitner P., Wolff C., Martin R. (2015b). Sometimes less is more: comparing the validity of complex problem solving measures. Intelligence 50 100–113. 10.1016/j.intell.2015.02.007 [ CrossRef ] [ Google Scholar ]
- Greiff S., Fischer A., Wüstenberg S., Sonnleitner P., Brunner M., Martin R. (2013a). A multitrait–multimethod study of assessment instruments for complex problem solving. Intelligence 41 579–596. 10.1016/j.intell.2013.07.012 [ CrossRef ] [ Google Scholar ]
- Greiff S., Holt D. V., Funke J. (2013b). Perspectives on problem solving in educational assessment: analytical, interactive, and collaborative problem solving. J. Problem Solv. 5 71–91. 10.7771/1932-6246.1153 [ CrossRef ] [ Google Scholar ]
- Greiff S., Wüstenberg S., Molnár G., Fischer A., Funke J., Csapó B. (2013c). Complex problem solving in educational contexts—something beyond g: concept, assessment, measurement invariance, and construct validity. J. Educ. Psychol. 105 364–379. 10.1037/a0031856 [ CrossRef ] [ Google Scholar ]
- Greiff S., Funke J. (2009). “Measuring complex problem solving: the MicroDYN approach,” in The Transition to Computer-Based Assessment. New Approaches to Skills Assessment and Implications for Large-Scale Testing , eds Scheuermann F., Björnsson J. (Luxembourg: Office for Official Publications of the European Communities; ), 157–163. [ Google Scholar ]
- Greiff S., Funke J. (2017). “Interactive problem solving: exploring the potential of minimal complex systems,” in The Nature of Problem Solving: Using Research to Inspire 21st Century Learning , eds Csapó B., Funke J. (Paris: OECD Publishing; ), 93–105. [ Google Scholar ]
- Greiff S., Martin R. (2014). What you see is what you (don’t) get: a comment on Funke’s (2014) opinion paper. Front. Psychol. 5 : 1120 10.3389/fpsyg.2014.01120 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Greiff S., Neubert J. C. (2014). On the relation of complex problem solving, personality, fluid intelligence, and academic achievement. Learn. Ind. Diff. 36 37–48. 10.1016/j.lindif.2014.08.003 [ CrossRef ] [ Google Scholar ]
- Greiff S., Niepel C., Scherer R., Martin R. (2016). Understanding students’ performance in a computer-based assessment of complex problem solving: an analysis of behavioral data from computer-generated log files. Comput. Hum. Behav. 61 36–46. 10.1016/j.chb.2016.02.095 [ CrossRef ] [ Google Scholar ]
- Greiff S., Stadler M., Sonnleitner P., Wolff C., Martin R. (2017). Sometimes more is too much: a rejoinder to the commentaries on Greif et al. (2015). J. Intell. 5 : 6 10.3390/jintelligence5010006 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Greiff S., Wüstenberg S. (2014). Assessment with microworlds using MicroDYN: measurement invariance and latent mean comparisons. Eur. J. Psychol. Assess. 1 1–11. 10.1027/1015-5759/a000194 [ CrossRef ] [ Google Scholar ]
- Greiff S., Wüstenberg S. (2015). Komplexer Problemlösetest COMPRO [Complex Problem-Solving Test COMPRO]. Mödling: Schuhfried. [ Google Scholar ]
- Greiff S., Wüstenberg S., Funke J. (2012). Dynamic problem solving: a new assessment perspective. Appl. Psychol. Measure. 36 189–213. 10.1177/0146621612439620 [ CrossRef ] [ Google Scholar ]
- Griffin P., Care E. (2015). “The ATC21S method,” in Assessment and Taching of 21st Century Skills , eds Griffin P., Care E. (Dordrecht, NL: Springer; ), 3–33. [ Google Scholar ]
- Güss C. D., Dörner D. (2011). Cultural differences in dynamic decision-making strategies in a non-linear, time-delayed task. Cogn. Syst. Res. 12 365–376. 10.1016/j.cogsys.2010.12.003 [ CrossRef ] [ Google Scholar ]
- Güss C. D., Tuason M. T., Orduña L. V. (2015). Strategies, tactics, and errors in dynamic decision making in an Asian sample. J. Dynamic Deci. Mak. 1 1–14. 10.11588/jddm.2015.1.13131 [ CrossRef ] [ Google Scholar ]
- Güss C. D., Wiley B. (2007). Metacognition of problem-solving strategies in Brazil, India, and the United States. J. Cogn. Cult. 7 1–25. 10.1163/156853707X171793 [ CrossRef ] [ Google Scholar ]
- Herde C. N., Wüstenberg S., Greiff S. (2016). Assessment of complex problem solving: what we know and what we don’t know. Appl. Meas. Educ. 29 265–277. 10.1080/08957347.2016.1209208 [ CrossRef ] [ Google Scholar ]
- Hermes M., Stelling D. (2016). Context matters, but how much? Latent state – trait analysis of cognitive ability assessments. Int. J. Sel. Assess. 24 285–295. 10.1111/ijsa.12147 [ CrossRef ] [ Google Scholar ]
- Hotaling J. M., Fakhari P., Busemeyer J. R. (2015). “Dynamic decision making,” in International Encyclopedia of the Social & Behavioral Sciences , 2nd Edn, eds Smelser N. J., Batles P. B. (New York, NY: Elsevier; ), 709–714. [ Google Scholar ]
- Hundertmark J., Holt D. V., Fischer A., Said N., Fischer H. (2015). System structure and cognitive ability as predictors of performance in dynamic system control tasks. J. Dynamic Deci. Mak. 1 1–10. 10.11588/jddm.2015.1.26416 [ CrossRef ] [ Google Scholar ]
- Jäkel F., Schreiber C. (2013). Introspection in problem solving. J. Problem Solv. 6 20–33. 10.7771/1932-6246.1131 [ CrossRef ] [ Google Scholar ]
- Jansson A. (1994). Pathologies in dynamic decision making: consequences or precursors of failure? Sprache Kogn. 13 160–173. [ Google Scholar ]
- Kaufman J. C., Beghetto R. A. (2009). Beyond big and little: the four c model of creativity. Rev. Gen. Psychol. 13 1–12. 10.1037/a0013688 [ CrossRef ] [ Google Scholar ]
- Knauff M., Wolf A. G. (2010). Complex cognition: the science of human reasoning, problem-solving, and decision-making. Cogn. Process. 11 99–102. 10.1007/s10339-010-0362-z [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Kretzschmar A. (2017). Sometimes less is not enough: a commentary on Greiff et al. (2015). J. Intell. 5 : 4 10.3390/jintelligence5010004 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Kretzschmar A., Neubert J. C., Wüstenberg S., Greiff S. (2016). Construct validity of complex problem solving: a comprehensive view on different facets of intelligence and school grades. Intelligence 54 55–69. 10.1016/j.intell.2015.11.004 [ CrossRef ] [ Google Scholar ]
- Kretzschmar A., Süß H.-M. (2015). A study on the training of complex problem solving competence. J. Dynamic Deci. Mak. 1 1–14. 10.11588/jddm.2015.1.15455 [ CrossRef ] [ Google Scholar ]
- Lee H., Cho Y. (2007). Factors affecting problem finding depending on degree of structure of problem situation. J. Educ. Res. 101 113–123. 10.3200/JOER.101.2.113-125 [ CrossRef ] [ Google Scholar ]
- Leutner D., Fleischer J., Wirth J., Greiff S., Funke J. (2012). Analytische und dynamische Problemlösekompetenz im Lichte internationaler Schulleistungsvergleichsstudien: Untersuchungen zur Dimensionalität. Psychol. Rundschau 63 34–42. 10.1026/0033-3042/a000108 [ CrossRef ] [ Google Scholar ]
- Luchins A. S. (1942). Mechanization in problem solving: the effect of einstellung. Psychol. Monogr. 54 1–95. 10.1037/h0093502 [ CrossRef ] [ Google Scholar ]
- Mack O., Khare A., Krämer A., Burgartz T. (eds) (2016). Managing in a VUCA world. Heidelberg: Springer. [ Google Scholar ]
- Mainert J., Kretzschmar A., Neubert J. C., Greiff S. (2015). Linking complex problem solving and general mental ability to career advancement: does a transversal skill reveal incremental predictive validity? Int. J. Lifelong Educ. 34 393–411. 10.1080/02601370.2015.1060024 [ CrossRef ] [ Google Scholar ]
- Mainzer K. (2009). Challenges of complexity in the 21st century. An interdisciplinary introduction. Eur. Rev. 17 219–236. 10.1017/S1062798709000714 [ CrossRef ] [ Google Scholar ]
- Meadows D. H., Meadows D. L., Randers J. (1992). Beyond the Limits. Vermont, VA: Chelsea Green Publishing. [ Google Scholar ]
- Meadows D. H., Meadows D. L., Randers J., Behrens W. W. (1972). The Limits to Growth. New York, NY: Universe Books. [ Google Scholar ]
- Meißner A., Greiff S., Frischkorn G. T., Steinmayr R. (2016). Predicting complex problem solving and school grades with working memory and ability self-concept. Learn. Ind. Differ. 49 323–331. 10.1016/j.lindif.2016.04.006 [ CrossRef ] [ Google Scholar ]
- Molnàr G., Greiff S., Wüstenberg S., Fischer A. (2017). “Empirical study of computer-based assessment of domain-general complex problem-solving skills,” in The Nature of Problem Solving: Using research to Inspire 21st Century Learning , eds Csapó B., Funke J. (Paris: OECD Publishing; ), 125–141. [ Google Scholar ]
- National Research Council (2011). Assessing 21st Century Skills: Summary of a Workshop. Washington, DC: The National Academies Press. [ PubMed ] [ Google Scholar ]
- Newell A., Shaw J. C., Simon H. A. (1959). A general problem-solving program for a computer. Comput. Automat. 8 10–16. [ Google Scholar ]
- Nisbett R. E., Wilson T. D. (1977). Telling more than we can know: verbal reports on mental processes. Psychol. Rev. 84 231–259. 10.1037/0033-295X.84.3.231 [ CrossRef ] [ Google Scholar ]
- OECD (2014). “PISA 2012 results,” in Creative Problem Solving: Students’ Skills in Tackling Real-Life problems , Vol. 5 (Paris: OECD Publishing; ). [ Google Scholar ]
- Osman M. (2010). Controlling uncertainty: a review of human behavior in complex dynamic environments. Psychol. Bull. 136 65–86. 10.1037/a0017815 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Osman M. (2012). The role of reward in dynamic decision making. Front. Neurosci. 6 : 35 10.3389/fnins.2012.00035 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Qudrat-Ullah H. (2015). Better Decision Making in Complex, Dynamic Tasks. Training with Human-Facilitated Interactive Learning Environments. Heidelberg: Springer. [ Google Scholar ]
- Ramnarayan S., Strohschneider S., Schaub H. (1997). Trappings of expertise and the pursuit of failure. Simulat. Gam. 28 28–43. 10.1177/1046878197281004 [ CrossRef ] [ Google Scholar ]
- Reuschenbach B. (2008). Planen und Problemlösen im Komplexen Handlungsfeld Pflege. Berlin: Logos. [ Google Scholar ]
- Rohe M., Funke J., Storch M., Weber J. (2016). Can motto goals outperform learning and performance goals? Influence of goal setting on performance, intrinsic motivation, processing style, and affect in a complex problem solving task. J. Dynamic Deci. Mak. 2 1–15. 10.11588/jddm.2016.1.28510 [ CrossRef ] [ Google Scholar ]
- Scherer R., Greiff S., Hautamäki J. (2015). Exploring the relation between time on task and ability in complex problem solving. Intelligence 48 37–50. 10.1016/j.intell.2014.10.003 [ CrossRef ] [ Google Scholar ]
- Schoppek W., Fischer A. (2015). Complex problem solving – single ability or complex phenomenon? Front. Psychol. 6 : 1669 10.3389/fpsyg.2015.01669 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Schraw G., Dunkle M., Bendixen L. D. (1995). Cognitive processes in well-defined and ill-defined problem solving. Appl. Cogn. Psychol. 9 523–538. 10.1002/acp.2350090605 [ CrossRef ] [ Google Scholar ]
- Schweizer F., Wüstenberg S., Greiff S. (2013). Validity of the MicroDYN approach: complex problem solving predicts school grades beyond working memory capacity. Learn. Ind. Differ. 24 42–52. 10.1016/j.lindif.2012.12.011 [ CrossRef ] [ Google Scholar ]
- Schweizer T. S., Schmalenberger K. M., Eisenlohr-Moul T. A., Mojzisch A., Kaiser S., Funke J. (2016). Cognitive and affective aspects of creative option generation in everyday life situations. Front. Psychol. 7 : 1132 10.3389/fpsyg.2016.01132 [ PMC free article ] [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Selten R., Pittnauer S., Hohnisch M. (2012). Dealing with dynamic decision problems when knowledge of the environment is limited: an approach based on goal systems. J. Behav. Deci. Mak. 25 443–457. 10.1002/bdm.738 [ CrossRef ] [ Google Scholar ]
- Simon H. A. (1957). Administrative Behavior: A Study of Decision-Making Processes in Administrative Organizations , 2nd Edn New York, NY: Macmillan. [ Google Scholar ]
- Sonnleitner P., Brunner M., Keller U., Martin R. (2014). Differential relations between facets of complex problem solving and students’ immigration background. J. Educ. Psychol. 106 681–695. 10.1037/a0035506 [ CrossRef ] [ Google Scholar ]
- Spering M., Wagener D., Funke J. (2005). The role of emotions in complex problem solving. Cogn. Emot. 19 1252–1261. 10.1080/02699930500304886 [ CrossRef ] [ Google Scholar ]
- Stadler M., Becker N., Gödker M., Leutner D., Greiff S. (2015). Complex problem solving and intelligence: a meta-analysis. Intelligence 53 92–101. 10.1016/j.intell.2015.09.005 [ CrossRef ] [ Google Scholar ]
- Stadler M., Niepel C., Greiff S. (2016). Easily too difficult: estimating item difficulty in computer simulated microworlds. Comput. Hum. Behav. 65 100–106. 10.1016/j.chb.2016.08.025 [ CrossRef ] [ Google Scholar ]
- Sternberg R. J. (1995). “Expertise in complex problem solving: a comparison of alternative conceptions,” in Complex Problem Solving: The European Perspective , eds Frensch P. A., Funke J. (Hillsdale, NJ: Erlbaum; ), 295–321. [ Google Scholar ]
- Sternberg R. J., Frensch P. A. (1991). Complex Problem Solving: Principles and Mechanisms. (eds) Sternberg R. J., Frensch P. A. Hillsdale, NJ: Erlbaum. [ Google Scholar ]
- Strohschneider S., Güss C. D. (1998). Planning and problem solving: differences between brazilian and german students. J. Cross-Cult. Psychol. 29 695–716. 10.1177/0022022198296002 [ CrossRef ] [ Google Scholar ]
- Strohschneider S., Güss C. D. (1999). The fate of the Moros: a cross-cultural exploration of strategies in complex and dynamic decision making. Int. J. Psychol. 34 235–252. 10.1080/002075999399873 [ CrossRef ] [ Google Scholar ]
- Thimbleby H. (2007). Press On. Principles of Interaction. Cambridge, MA: MIT Press. [ Google Scholar ]
- Tobinski D. A., Fritz A. (2017). “EcoSphere: a new paradigm for problem solving in complex systems,” in The Nature of Problem Solving: Using Research to Inspire 21st Century Learning , eds Csapó B., Funke J. (Paris: OECD Publishing; ), 211–222. [ Google Scholar ]
- Tremblay S., Gagnon J.-F., Lafond D., Hodgetts H. M., Doiron M., Jeuniaux P. P. J. M. H. (2017). A cognitive prosthesis for complex decision-making. Appl. Ergon. 58 349–360. 10.1016/j.apergo.2016.07.009 [ PubMed ] [ CrossRef ] [ Google Scholar ]
- Tschirgi J. E. (1980). Sensible reasoning: a hypothesis about hypotheses. Child Dev. 51 1–10. 10.2307/1129583 [ CrossRef ] [ Google Scholar ]
- Tuchman B. W. (1984). The March of Folly. From Troy to Vietnam. New York, NY: Ballantine Books. [ Google Scholar ]
- Verweij M., Thompson M. (eds) (2006). Clumsy Solutions for A Complex World. Governance, Politics and Plural Perceptions. New York, NY: Palgrave Macmillan; 10.1057/9780230624887 [ CrossRef ] [ Google Scholar ]
- Viehrig K., Siegmund A., Funke J., Wüstenberg S., Greiff S. (2017). “The heidelberg inventory of geographic system competency model,” in Competence Assessment in Education. Research, Models and Instruments , eds Leutner D., Fleischer J., Grünkorn J., Klieme E. (Heidelberg: Springer; ), 31–53. [ Google Scholar ]
- von Clausewitz C. (1832). Vom Kriege [On war]. Berlin: Dämmler. [ Google Scholar ]
- Wendt A. N. (2017). The empirical potential of live streaming beyond cognitive psychology. J. Dynamic Deci. Mak. 3 1–9. 10.11588/jddm.2017.1.33724 [ CrossRef ] [ Google Scholar ]
- Wiliam D., Black P. (1996). Meanings and consequences: a basis for distinguishing formative and summative functions of assessment? Br. Educ. Res. J. 22 537–548. 10.1080/0141192960220502 [ CrossRef ] [ Google Scholar ]
- World Economic Forum (2015). New Vsion for Education Unlocking the Potential of Technology. Geneva: World Economic Forum. [ Google Scholar ]
- World Economic Forum (2016). Global Risks 2016: Insight Report , 11th Edn Geneva: World Economic Forum. [ Google Scholar ]
- Wüstenberg S., Greiff S., Funke J. (2012). Complex problem solving — more than reasoning? Intelligence 40 1–14. 10.1016/j.intell.2011.11.003 [ CrossRef ] [ Google Scholar ]
- Wüstenberg S., Greiff S., Vainikainen M.-P., Murphy K. (2016). Individual differences in students’ complex problem solving skills: how they evolve and what they imply. J. Educ. Psychol. 108 1028–1044. 10.1037/edu0000101 [ CrossRef ] [ Google Scholar ]
- Wüstenberg S., Stadler M., Hautamäki J., Greiff S. (2014). The role of strategy knowledge for the application of strategies in complex problem solving tasks. Technol. Knowl. Learn. 19 127–146. 10.1007/s10758-014-9222-8 [ CrossRef ] [ Google Scholar ]
- SUGGESTED TOPICS
- The Magazine
- Newsletters
- Managing Yourself
- Managing Teams
- Work-life Balance
- The Big Idea
- Data & Visuals
- Reading Lists
- Case Selections
- HBR Learning
- Topic Feeds
- Account Settings
- Email Preferences
Share Podcast

The Right Way to Solve Complex Business Problems
Corey Phelps, a strategy professor at McGill University, says great problem solvers are hard to find. Even seasoned professionals at the highest levels of organizations regularly...
- Apple Podcasts
Corey Phelps, a strategy professor at McGill University, says great problem solvers are hard to find. Even seasoned professionals at the highest levels of organizations regularly fail to identify the real problem and instead jump to exploring solutions. Phelps identifies the common traps and outlines a research-proven method to solve problems effectively. He’s the coauthor of the book, Cracked it! How to solve big problems and sell solutions like top strategy consultants.
Download this podcast
Welcome to the IdeaCast from Harvard Business Review. I’m Curt Nickisch.
Problem-solving is in demand. It’s considered the top skill for success at management consulting firms. And it’s increasingly desired for everyone, not just new MBA’s.
A report from the World Economic Forum predicts that more than one-third of all jobs across all industries will require complex problem-solving as one of their core skills by 2020.
The problem is, we’re often really bad at problem-solving. Our guest today says even the most educated and experienced of senior leaders go about it the wrong way.
COREY PHELPS: I think this is one of the misnomers about problem-solving. There’s this belief that because we do it so frequently – and especially for senior leaders, they have a lot of experience, they solve problems for a living – and as such we would expect them to be quite good at it. And I think what we find is that they’re not. They don’t solve problems well because they fall prey to basically the foibles of being a human being – they fall prey to the cognitive biases and the pitfalls of problem-solving.
CURT NICKISCH: That’s Corey Phelps. He says fixing these foibles is possible and almost straightforward. You can improve your problem-solving skills by following a disciplined method.
Corey Phelps is a strategy professor at McGill University. He’s also the co-author of the book “Cracked It: How to Solve Big Problems and Sell Solutions like Top Strategy C onsultants.” Corey thanks for coming on the show.
COREY PHELPS: Thank you for the opportunity to talk.
CURT NICKISCH: Another probably many, many biases that prevent people from solving big problems well.
COREY PHELPS: Absolutely.
CURT NICKISCH: What are some of the most common, or your favorite stumbling blocks?
COREY PHELPS: Well, one of my favorites is essentially the problem of jumping to solutions or the challenge of jumping to solutions.
CURT NICKISCH: Oh, come on Corey. That’s so much fun.
COREY PHELPS: It is, and it’s very much a result of how our brains have evolved to process information, but it’s my favorite because we all do it. And especially I would say it happens in organizations because in organizations when you layer on these time pressures and you layer on these concerns about efficiency and productivity, it creates enormous, I would say incentive to say “I don’t have time to carefully define and analyze the problem. I got to get a solution. I got to implement it as quick as possible.” And the fundamental bias I think is, is illustrated beautifully by Danny Kahneman in his book “Thinking, Fast and Slow,” is that our minds are essentially hardwired to think fast.
We are able to pay attention to a tiny little bit of information. We can then weave a very coherent story that makes sense to us. And then we can use that story to jump very quickly to a solution that we just know will work. And if we just were able to move from that approach of what Kahneman and cognitive psychologists called “System 1 thinking” to “System 2 thinking” – that is to slow down, be more deliberative, be more structured – we would be able to better understand the problem that we’re trying to solve and be more effective and exhaustive with the tools that we want to use to understand the problem before we actually go into solution-generation mode.
CURT NICKISCH: Complex problems demand different areas of expertise and often as individuals we’re coming to those problems with one of them. And I wonder if that’s often the problem of problem-solving, which is that a manager is approaching it from their own expertise and because of that, they see the problem through a certain way. Is that one of the cognitive biases that stop people from being effective problem solvers?
COREY PHELPS: Yeah. That’s often referred to as the expertise trap. It basically colors and influences what we pay attention to with respect to a particular problem. And it limits us with respect to the tools that we can bring to bear to solve that problem. In the world of psychology, there’s famous psychologist, Abraham Maslow, who is famous for the hierarchy of needs. He’s also famous for something that was a also known as MaSlow’s axiom, Maslow’s law. It’s also called the law of the instrument, and to paraphrase Maslow, he basically said, “Look, I suppose if the only tool that you have in your toolkit is a hammer, everything looks like a nail.”
His point is that if you’re, for example, a finance expert and your toolkit is the toolkit of let’s say, discounted cash flow analysis for valuation, then you’re going to see problems through that very narrow lens. Now, one of the ways out of this, I think to your point is collaboration becomes fundamentally important. And collaboration starts with the recognition that I don’t have all of the tools, all of the knowledge in me to effectively solve this. So I need to recruit people that can actually help me.
CURT NICKISCH: That’s really interesting. I wonder how much the fact that you have solved a problem before it makes you have a bias for that same solution for future problems?
COREY PHELPS: Yeah, that’s a great question. What you’re alluding to is analogical reasoning, and we know that human beings, one of the things that allows us to operate in novel settings is that we can draw on our past experience. And we do so when it comes to problem solving, often times without being conscious or mentally aware of it. We reach into our memory and we ask ourselves a very simple question: “Have I seen a problem like this before?”
And if it looks familiar to me, the tendency then is to say, “Okay, well what worked in solving that problem that I faced before?” And then to say, “Well, if it worked in that setting, then it should work in this setting.” So that’s reasoning by analogy.
Reasoning by analogy has a great upside. It allows human beings to not become overwhelmed by the tremendous novelty that they face in their daily lives. The downside is that if we don’t truly understand it at sort of a deep level, whether or not the two problems are similar or different, then we can make what cognitive psychologists called surface-level analogies.
And we can then say, “Oh, this looks a lot like the problem I faced before, that solution that worked there is going to easily work here.” And we try that solution and it fails and it fails largely because if we dug a little bit deeper, the two problems actually aren’t much alike at all in terms of their underlying causes.
CURT NICKISCH: The starkest example of this, I think, in your book is Ron Johnson who left Apple to become CEO of JC Penney. Can you talk about that a little bit and what that episode for the company says about this?
COREY PHELPS: So yes, its – Ron Johnson had been hired away from Target in the United States to, by Steve Jobs to help create Apple stores. Apple stores are as many people know the most successful physical retailer on the planet measured by, for example, sales per square foot or per square meter. He’s got the golden touch. He’s created this tremendously successful retail format for Apple.
So the day that it was announced that Ron Johnson was going to step into the CEO role at JC Penney, the stock price of JC Penney went up by almost 18 percent. So clearly he was viewed as the savior. Johnson moves very, very quickly. Within a few months, he announces that he has a strategic plan and it basically comes in three parts.
Part number one is he’s going to eliminate discount pricing. JC Penney had been a very aggressive sales promoter. The second piece of it is he’s going to completely change how they organize merchandise. It’s no longer going to be organized by function – so menswear, housewares, those sorts of things. It’s going to be organized by boutique, so there’s going to be a Levi’s boutique, a Martha Stewart Boutique, a Joe Fresh Boutique and so on.
And it would drop the JC P enney name, they would call it JCP. And he rolls this out over the course of about 12 months across the entire chain of over 1100 stores. What this tells us, he’s so confident in his solution, his strategic transformation, that he doesn’t think it’s worth it to test this out on one or two pilot stores.
CURT NICKISCH: Yeah, he was quoted as saying: “At Apple, we didn’t test anything.”
COREY PHELPS: We didn’t test. Yes. What worked at Apple, he assumed would work at JC Penney. And the critical thing that I think he missed is that JC Penney customers are very different from Apple store customers. In fact, JC Penney customers love the discount. They love the thrill of hunting for a deal.
CURT NICKISCH: Which seems so fundamental to business, right? Understanding your customer. It’s just kind of shocking, I guess, to hear the story.
COREY PHELPS: It is shocking and especially when you consider that Ron Johnson had spent his entire career in retail, so this is someone that had faced, had seen, problems in retailers for decades – for over three decades by the time that he got to JC Penney. So you would expect someone with that degree of experience in that industry wouldn’t make that leap of, well, what worked at Apple stores is going to work at JC Penney stores, but in fact that’s exactly what happened.
CURT NICKISCH: In your book, you essentially suggest four steps that you recommend people use. Tell us about the four steps then.
COREY PHELPS: So in the book we describe what we call the “Four S method,” so four stages, each of which starts with the letter “s”. So the first stage is “state the problem.” Stating the problem is fundamentally about defining what the problem is that you are attempting to solve.
CURT NICKISCH: And you probably would say don’t hurry over that first step or the other three are going to be kind of pointless.
COREY PHELPS: Yeah, that’s exactly the point of of laying out the four s’s. There’s a tremendous amount of desire even amongst senior executives to want to get in and fix the problem. In other words, what’s the trouble? What are the symptoms? What would define success? What are the constraints that we would be operating under? Who owns the problem? And then who are the key stakeholders?
Oftentimes that step is skipped over and we go right into, “I’ve got a hypothesis about what I think the solution is and I’m so obsessed with getting this thing fixed quickly, I’m not going to bother to analyze it particularly well or test the validity of my assumptions. I’m going to go right into implementation mode.”
The second step, what we call “structure the problem” is once you have defined the problem, you need to then start to identify what are the potential causes of that problem. So there are different tools that we talked about in the book that you can structure a problem for analysis. Once you’ve structured the problem for analysis and you’ve conducted the analysis that helps you identify what are the underlying causes that are contributing to it, which will then inform the third stage which is generating solutions for the problem and then testing and evaluating those solutions.
CURT NICKISCH: Is the danger that that third step – generating solutions – is the step that people spend the most time on or have the most fun with?
COREY PHELPS: Yeah. The danger is, is that what that’s naturally what people gravitate towards. So we want to skip over the first two, state and structure.
CURT NICKISCH: As soon as you said it, I was like, “let’s talk about that more.”
COREY PHELPS: Yeah. And we want to jump right into solutioning because people love to talk about their ideas that are going to fix the problem. And that’s actually a useful way to frame a discussion about solutions – we could, or we might do this – because it opens up possibilities for experimentation.
And the problem is that when we often talk about what we could do, we have very little understanding of what the problem is that we’re trying to solve and what are the underlying causes of that problem. Because as you said, solution generation is fun. Look, the classic example is brainstorming. Let’s get a bunch of people in a room and let’s talk about the ideas on how to fix this thing. And again, be deliberate, be disciplined. Do those first stages, the first two stages – state and structure – before you get into the solution generation phase.
CURT NICKISCH: Yeah. The other thing that often happens there is just the lack of awareness of just the cost of the different solutions – how much time, or what they would actually take to do.
COREY PHELPS: Yeah, and again, I’ll go back to that example I used of brainstorming where it’s fun to get a group of people together and talk about our ideas and how to fix the problem. There’s a couple challenges of that. One is what often happens when we do that is we tend to censor the solutions that we come up with. In other words, we ask ourselves, “if I say this idea, people are gonna, think I’m crazy, or people going to say: that’s stupid, that’ll never work, we can’t do that in our organization. It’s going to be too expensive, it’s going to take too much time. We don’t have the resources to do it.”
So brainstorming downside is we we self-sensor, so that’s where you need to have deep insight into your organization in terms of A. what’s going to be feasible, B. what’s going to be desirable on the part of the people that actually have the problem, who you’re trying to solve the problem for and C. from a business standpoint, is it going to be financially attractive for us?
So applying again a set of disciplined criteria that help you choose amongst those ideas for potential solutions. Then the last stage of the process which is selling – because it’s rare in any organization that someone or the group of people that come up with the solution actually have the power and the resources to implement it, so that means they’re going to have to persuade other people to buy into it and want to help.
CURT NICKISCH: Design thinking is another really different method essentially for solving problems or coming up with solutions that just aren’t arrived at through usual problem-solving or usual decision-making processes. I’m just wondering how design thinking comes to play when you’re also outlining these, you know, disciplined methods for stating and solving problems.
COREY PHELPS: For us it’s about choosing the right approach. You know what the potential causes of a problem are. You just don’t know which ones are operating in the particular problem you’re trying to solve. And what that means is that you’ve got a theory – and this is largely the world of strategy consultants – strategy consultants have theories. They have, if you hear them speak, deep understanding of different types of organizational problems, and what they bring is an analytic tool kit that says, “first we’re going to identify all the possible problems, all the possible causes I should say, of this problem. We’re going to figure out which ones are operating and we’re going to use that to come up with a solution.” Then you’ve got problems that you have no idea what the causes are. You’re in a world of unknown unknowns or unk-unks as the operations management people call them.
CURT NICKISCH: That’s terrible.
COREY PHELPS: In other words, you don’t have a theory. So the question is, how do you begin? Well, this is where design thinking can be quite valuable. Design thinking says: first off, let’s find out who are the human beings, the people that are actually experiencing this problem, and let’s go out and let’s talk to them. Let’s observe them. Let’s immerse ourselves in their experience and let’s start to develop an understanding of the causes of the problem from their perspective.
So rather than go into it and say, “I have a theory,” let’s go the design thinking route and let’s actually based upon interactions with users or customers, let’s actually develop a theory. And then we’ll use our new understanding or new insight into the causes of the problem to move into the solution generation phase.
CURT NICKISCH: Problem-solving – we know that that’s something that employers look for when they’re recruiting people. It is one of those phrases that, you know, I’m sure somebody out there has, has the title at a company Chief Problem Solver instead of CEO, right? So, it’s almost one of those phrases that so over used it can lose its meaning.
And if you are being hired or you’re trying to make a case for being on a team that’s tackling a problem, how do you make a compelling case that you are a good problem solver? How can you actually show it?
COREY PHELPS: It’s a great question and then I have two answers to this question. So one is, look at the end of the day, the proof is in the pudding. In other words, can you point to successful solutions that you’ve come up with – solutions that have actually been effective in solving a problem? So that’s one.
The second thing is can you actually articulate how you approach problem-solving? In other words, do you follow a method or are you reinventing the wheel every time you solve a problem? Is it an ad hoc approach? And I think this issue really comes to a head when it comes to the world of strategy consulting firms when they recruit. For example, Mckinsey, you’ve got the Mckinsey problem-solving test, which is again, a test that’s actually trying to elicit the extent to which people are good applicants are good at solving problems
And then you’ve got the case interview. And in the case interview, what they’re looking at is do you have a mastery over certain tools. But what they’re really looking at is, are you actually following a logical process to solve this problem? Because again, what they’re interested in is finding- to your point – people that are going to be good at solving complex organizational problems. So they’re trying to get some evidence that they can demonstrate that they’re good at it and some evidence that they follow a deliberate process.
CURT NICKISCH: So even if you’re not interviewing at a consulting firm, that’s a good approach, to show your thinking, show your process, show the questions you ask?
COREY PHELPS: Yeah, and to your point earlier, at least if we look at what recruiters of MBA students are saying these days, they’re saying, for example, according to the FT’s recent survey, they’re saying that we want people with really good problem solving skills, and by the same token, we find that that’s a skill that’s difficult for us to recruit for. And that reinforces our interest in this area because the fundamental idea for the book is to give people a method. We’re trying to equip not just MBA students but everybody that’s going to face complex problems with a toolkit to solve them better.
CURT NICKISCH: Corey, this has been really great. Thank you.
COREY PHELPS: Thanks for the opportunity. I appreciate it.
CURT NICKISCH: That’s Corey Phelps. He teaches strategy at McGill University, and he co-wrote the book “Cracked It: How to Solve Big Problems and Sell Solutions Like Top Strategy Consultants.”
This episode was produced by Mary Dooe. We got technical help from Rob Eckhardt. Adam Buchholz is our audio product manager.
Thanks for listening to the HBR IdeaCast. I’m Curt Nickisch.
- Subscribe On:
Latest in this series
This article is about decision making and problem solving, partner center.

Serving technical professionals globally for over 75 years. Learn more about us.
MIT Professional Education 700 Technology Square Building NE48-200 Cambridge, MA 02139 USA
Accessibility
Solving Complex Problems: Structured Thinking, Design Principles, and AI
Sang-Gook Kim
Download the Course Schedule
How do you solve important, large-scale challenges with evolving and contradictory constraints? In this 5-day course, transform your approach to large-scale problem solving, from multi-stakeholder engineering projects to the online spread of misinformation. Alongside engineers and leaders from diverse industries, you’ll explore actionable innovative frameworks for assessing, communicating, and implementing complex systems—and significantly increase your likelihood of success.
THIS COURSE MAY BE TAKEN INDIVIDUALLY OR AS PART OF THE PROFESSIONAL CERTIFICATE PROGRAM IN INNOVATION & TECHNOLOGY OR THE PROFESSIONAL CERTIFICATE PROGRAM IN DESIGN & MANUFACTURING .
Engineering projects with shifting goals. Inefficient national healthcare systems. The online spread of misinformation. Every day, professionals are tasked with addressing major challenges that present opportunities for great triumph—or significant failure. How do you approach an important, large-scale challenge with evolving and contradictory constraints? Is the solution a new technology, a new policy, or something else altogether? In our new course Solving Complex Problems: Structured Thinking, Design Principles, and AI , you’ll acquire core principles that will change the way you approach and solve large-scale challenges—increasing your likelihood of success. Over the course of five days, you will explore proven design principles, heuristic-based insights, and problem-solving approaches, and learn how to persuasively present concepts and system architectures to stakeholders. Methods utilize recent developments in AI and Big Data, as well as innovative strategies from MIT Lincoln Laboratory that have been successfully applied to large and complex national defense systems. By taking part in interactive lectures and hands-on projects, you will learn to think through and leverage important steps, including problem abstraction, idea generation, concept development and refinement, system-level thinking, and proposal generation. Alongside an accomplished group of global peers, you will explore the strategies and frameworks you need to implement large-scale systems that can have a significant positive impact—and minimize the probability of failure.
Certificate of Completion from MIT Professional Education

- Approach and solve large and complex problems.
- Assess end-to-end processes and associated challenges, in order to significantly increase the likelihood of success in developing more complex systems.
- Implement effective problem-solving techniques, including abstracting the problem, idea generation, concept development and refinement, system-level thinking, and proposal generation.
- Utilize system-level thinking skills to evaluate, refine, down select, and evaluate best ideas and concepts.
- Apply the Axiomatic Design methodology to a broad range of applications in manufacturing, product design, software, and architecture.
- Generate and present proposals that clearly articulate innovative ideas, clarify the limits of current strategies, define potential customers and impact, and outline a success-oriented system development and risk mitigation plan.
- Effectively communicate ideas and persuade others, and provide valuable feedback.
- Confidently develop and execute large-scale system concepts that will drive significant positive impact.
Edwin F. David Head of the Engineering Division, MIT Lincoln Laboratory
Jonathan E. Gans Group Leader of the Systems and Architectures Group, MIT Lincoln Laboratory
Robert T-I. Shin Principal Staff in the Intelligence, Surveillance, and Reconnaissance (ISR) and Tactical Systems Division, MIT Lincoln Laboratory Director, MIT Beaver Works
This course is appropriate for professionals who design or manage complex systems with shifting needs and goals. It is also well suited to those who want to improve the quality and performance of their operations and decision-making in a large-scale system environment. Potential participants include engineers, group leaders, and senior managers in government and industries including automotive, aerospace, semiconductors, engineering, manufacturing, healthcare, bio-medical, finance, architecture, public policy, education, and military.
Computer Requirements
A laptop with PowerPoint is required.

- InterviewPenguin.com – Your best job interview coach since 2011
Tell me about a time when you have a simple solution to a complex problem – Interview questions answered
The best companies in the world always strive to improve , at each level of the organization. Innovating and changing processes, the employees, and in particular the engineers and managers , face problems on a daily basis. Some of them are simple and won’t make your head spin, but in the most successful companies in the world, such as Amazon or Google , you will often face the unknown, having to deal with a serious issue (typically of a technical or managerial character). Needless to say, hiring managers wonder if you have such an experience, and how you handled a similar situation in the past.
In an ideal case, you should talk about a relevant problem, which means a type of an issue you can realistically face in your new job as well. If you lack such an experience, however, and do not want to make something up, you can also narrate a difficult situation you had to handle at school, or even in your personal life. At the end of the day, your attitude matters more than anything else to the interviewers. And what attitude they are looking for?
In this particular case, they are looking for your ability to simplify things . They want to hear that you can think outside of the box , and do not look only for obvious solution–which are typically complex when we deal with complex problems. On the contrary, you can come up with unexpected solutions, saving both time and resources of yourself and your employer. Easier to say than do in reality :), but let’s have a look at some sample answers, and hopefully after reading them you will know what to say in your job interview.

7 sample answers to “Describe a time when you have a simple solution to a complex problem.”
- I remember such a situation from my last engineering job . Facing a tricky app development task, a team of developers were stuck at one point. They were just adding new layers to the code, making the entire app more robust and complex , which isn’t the worst thing, but such an app is prone to bugs and issues , and once something gets wrong it is harder to troubleshoot it. I was overseeing the project, and I was worried. At the end of the day I knew we had to make things differently , unless we wanted to miss the deadline. And so I spent two days talking to other engineers, brainstorming ideas. Eventually I came with a simple workaround , using a functionality of an already existing app of one of our business partners, which allowed us to simplify the code of our own app, and move to the next stage of the development. It was just one of these situations when we tried to reinvent the wheel… It took me some time to realize it, and I was the only one in the team to see it, but I did see it and solved this complex issue with a simple solution.
- I remember one from my last managerial job in a big logistics center. Things just weren’t working well there–that’s why I got the job at the first place. The last managers tried to improve the workflow in countless ways, but they still failed to reach the productivity targets expected by the executives. They were improving many processes, but somehow they still failed to get things done. When I stepped in, instead of complicating things, I had a one on one meeting with every single employee of the place , including the janitors. With some people I talked for five minutes only, with some managers I talked for an hour. I tried to be very honest and expected the same from the people I met. After a week I came to a conclusion that the core of the problem didn’t consists in bad processes. We just didn’t have enough people in some teams to keep the workflow going, and to avoid delays. I hired two new employees and contracted three other through a staffing agency. The next month we reached the desired productivity levels and didn’t miss a single deadline. Hence I solved this complex problem, which my predecessors failed to solve in more than a year.
- This is my first job application , and logically I cannot recall such a situation from work. However, I can talk about a situation from my personal life. As a young man I faced depression . My parents sent me to one specialist after another, and I went to group therapy and what not. Doctors also prescribed me some medications, but deep down I knew it wasn’t a way to go , since every medication has side effects, and I didn’t want to eat pills for the rest of my life. Hence I decided to make a radical change to my diet : I stopped drinking coffee and alcohol, and I stopped consuming sugar and meat. It was a radical move, and not an easy to make in a country where they put sugar everywhere. But once I found what I could eat and drink, it was just a question of forming a habit, and getting rid of my addictions (to sugar and coffee). The changes in diet had a profound impact on both my energy levels and mental well-being. I was able to dash all the specialists and medications, and I can proclaim now that I haven’t felt depressed in years. My problem seemed complex, and people around me tried to solve it in a complex way. But my experience taught me that it is often better looking for simple solutions , and that we shouldn’t be afraid to think outside of the box. I want to maintain this attitude in my working life.
- The best example is perhaps my last employment at Tesla . I really tried to make things work for me there, though I wasn’t on the same page with leaders when it came to many issues. Initially I tried to convince them, coming up with arguments and presentations, trying to win them over. Looking at it retrospectively, I wasted so many hours trying to prove my point…. Eventually I realized it was not going to work, because the direction I wanted to take just didn’t get along with the philosophy of the company, and with the goals they tried to achieve with the particular product line. And so I quit . It was the simplest solution to the complex problem of my employment with Tesla. Instead of trying to change a big company, I changes something in my own life. And here I am, trying to get a job with you…
- In my opinion, complex problems demand complex solutions . Of course, people like to believe in miracles . Such as that the entire planet will become vegan and it will solve the climate change crisis we face right now in the world. But that’s not how things work in reality, in this world where everything relates to everything . When I face a complex problem, I try to break it down to smaller issues , to smaller problems which I can address personally, or someone in my team can, or an external provider. And then I simply address them one by one , in the right order. For an outsider it may look like we are solving simple issues, but in fact we are addressing a complex problem with a complex solution . This is how I worked in my last job, and I want to apply the same principles in my new job with you.
- The best example I can come up with from my young life is when I made a bet with my friend that I would run a marathon within a year. It was four years ago, I was overweight, and could not run for hundred yards, let alone a marathon. At first I thought about complex changes to my life–such as quitting smoking, changing my diet, working with a running coach, etc. But I quickly realized that I did not have time for it , and had to come up with something else. Hence I simply decided to run every day , progressively prolonging my distance, and increasing my pace. I started with one mile slow jog, and though it was very hard at the beginning, I got used to it in two weeks, and started to prolong my distance and quicken my pace. Before I knew it six month had passed, I was fitter than ever and running five miles a day. I ran my first marathon in less than four hours, and the entire experience taught me an important lesson about simple solutions to relatively complex problems–both in life and in work.
- I faced such an issue when writing a code for XYZ app in my present job. I knew I could address the problem we had with a loop in different ways. One was easy, and it could be done in thirty minutes , but it wasn’t a complex solution, and in later stages of the development it could actually backfire. Surely, someone else would take the bullet then, working on the later stages, or testing the app. But I did not want it to happen. So I opted for a more complex solution that took me an entire day to implement , but I knew that once we had it in place, other developers would not deal with the same problem in later stages of the project. Looking at the things from perspective, I believe I took the best action for the entire team . And that’s always my attitude: I do not look for a simple solution. I look for the best solution for the entire team, and I always try to see the bigger picture…
Ready to answer this tricky interview question? I hope so! Do not forget to check also sample answers to other tricky questions you may face while trying to get any good managerial or engineering job:
- Tell me about a time when you used logic to solve a problem .
- Tell me about a time when you had to give a difficult feedback to someone.
- Describe a situation when you didn’t know how to solve a problem .
- Recent Posts
© InterviewPenguin.com
Privacy Policy
Help | Advanced Search
Computer Science > Artificial Intelligence
Title: solving for x and beyond: can large language models solve complex math problems with more-than-two unknowns.
Abstract: Large Language Models (LLMs) have demonstrated remarkable performance in solving math problems, a hallmark of human intelligence. Despite high success rates on current benchmarks; however, these often feature simple problems with only one or two unknowns, which do not sufficiently challenge their reasoning capacities. This paper introduces a novel benchmark, BeyondX, designed to address these limitations by incorporating problems with multiple unknowns. Recognizing the challenges in proposing multi-unknown problems from scratch, we developed BeyondX using an innovative automated pipeline that progressively increases complexity by expanding the number of unknowns in simpler problems. Empirical study on BeyondX reveals that the performance of existing LLMs, even those fine-tuned specifically on math tasks, significantly decreases as the number of unknowns increases - with a performance drop of up to 70\% observed in GPT-4. To tackle these challenges, we propose the Formulate-and-Solve strategy, a generalized prompting approach that effectively handles problems with an arbitrary number of unknowns. Our findings reveal that this strategy not only enhances LLM performance on the BeyondX benchmark but also provides deeper insights into the computational limits of LLMs when faced with more complex mathematical challenges.
| Subjects: | Artificial Intelligence (cs.AI); Computation and Language (cs.CL); Machine Learning (cs.LG) |
| Cite as: | [cs.AI] |
| (or [cs.AI] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
For IEEE Members
Ieee spectrum, follow ieee spectrum, support ieee spectrum, enjoy more free content and benefits by creating an account, saving articles to read later requires an ieee spectrum account, the institute content is only available for members, downloading full pdf issues is exclusive for ieee members, downloading this e-book is exclusive for ieee members, access to spectrum 's digital edition is exclusive for ieee members, following topics is a feature exclusive for ieee members, adding your response to an article requires an ieee spectrum account, create an account to access more content and features on ieee spectrum , including the ability to save articles to read later, download spectrum collections, and participate in conversations with readers and editors. for more exclusive content and features, consider joining ieee ., join the world’s largest professional organization devoted to engineering and applied sciences and get access to all of spectrum’s articles, archives, pdf downloads, and other benefits. learn more about ieee →, join the world’s largest professional organization devoted to engineering and applied sciences and get access to this e-book plus all of ieee spectrum’s articles, archives, pdf downloads, and other benefits. learn more about ieee →, access thousands of articles — completely free, create an account and get exclusive content and features: save articles, download collections, and talk to tech insiders — all free for full access and benefits, join ieee as a paying member., how good is chatgpt at coding, really, study finds that while ai can be great, it also struggles due to training limitations.

This article is part of our exclusive IEEE Journal Watch series in partnership with IEEE Xplore.
Programmers have spent decades writing code for AI models , and now, in a full circle moment, AI is being used to write code. But how does an AI code generator compare to a human programmer?
A study published in the June issue of IEEE Transactions on Software Engineering evaluated the code produced by OpenAI’s ChatGPT in terms of functionality, complexity and security. The results show that ChatGPT has an extremely broad range of success when it comes to producing functional code—with a success rate ranging from anywhere as poor as 0.66 percent and as good as 89 percent—depending on the difficulty of the task, the programming language, and a number of other factors.
While in some cases the AI generator could produce better code than humans, the analysis also reveals some security concerns with AI-generated code.
Yutian Tang is a lecturer at the University of Glasgow who was involved in the study. He notes that AI-based code generation could provide some advantages in terms of enhancing productivity and automating software development tasks—but it’s important to understand the strengths and limitations of these models.
“By conducting a comprehensive analysis, we can uncover potential issues and limitations that arise in the ChatGPT-based code generation... [and] improve generation techniques,” Tang explains.
To explore these limitations in more detail, his team sought to test GPT-3.5’s ability to address 728 coding problems from the LeetCode testing platform in five programming languages: C, C++, Java, JavaScript, and Python .
“A reasonable hypothesis for why ChatGPT can do better with algorithm problems before 2021 is that these problems are frequently seen in the training dataset.” —Yutian Tang, University of Glasgow
Overall, ChatGPT was fairly good at solving problems in the different coding languages—but especially when attempting to solve coding problems that existed on LeetCode before 2021. For instance, it was able to produce functional code for easy, medium, and hard problems with success rates of about 89, 71, and 40 percent, respectively.
“However, when it comes to the algorithm problems after 2021, ChatGPT’s ability to generate functionally correct code is affected. It sometimes fails to understand the meaning of questions, even for easy level problems,” Tang notes.
For example, ChatGPT’s ability to produce functional code for “easy” coding problems dropped from 89 percent to 52 percent after 2021. And its ability to generate functional code for “hard” problems dropped from 40 percent to 0.66 percent after this time as well.
“A reasonable hypothesis for why ChatGPT can do better with algorithm problems before 2021 is that these problems are frequently seen in the training dataset,” Tang says.
Essentially, as coding evolves, ChatGPT has not been exposed yet to new problems and solutions. It lacks the critical thinking skills of a human and can only address problems it has previously encountered. This could explain why it is so much better at addressing older coding problems than newer ones.
“ChatGPT may generate incorrect code because it does not understand the meaning of algorithm problems.” —Yutian Tang, University of Glasgow
Interestingly, ChatGPT is able to generate code with smaller runtime and memory overheads than at least 50 percent of human solutions to the same LeetCode problems.
The researchers also explored the ability of ChatGPT to fix its own coding errors after receiving feedback from LeetCode. They randomly selected 50 coding scenarios where ChatGPT initially generated incorrect coding, either because it didn’t understand the content or problem at hand.
While ChatGPT was good at fixing compiling errors, it generally was not good at correcting its own mistakes.
“ChatGPT may generate incorrect code because it does not understand the meaning of algorithm problems, thus, this simple error feedback information is not enough,” Tang explains.
The researchers also found that ChatGPT-generated code did have a fair amount of vulnerabilities, such as a missing null test, but many of these were easily fixable. Their results also show that generated code in C was the most complex, followed by C++ and Python, which has a similar complexity to the human-written code.
Tangs says, based on these results, it’s important that developers using ChatGPT provide additional information to help ChatGPT better understand problems or avoid vulnerabilities.
“For example, when encountering more complex programming problems, developers can provide relevant knowledge as much as possible, and tell ChatGPT in the prompt which potential vulnerabilities to be aware of,” Tang says.
- What to Do When the Ghost in the Machine Is You ›
- How Coders Can Survive—and Thrive—in a ChatGPT World ›
- Coding Assistant - ChatGPT ›
Michelle Hampson is a freelance writer based in Halifax. She frequently contributes to Spectrum's Journal Watch coverage, which highlights newsworthy studies published in IEEE journals.
That's yesterday's news, try it with version 4o, it's free.
"struggles due to training limitations" isn't that EVERYONE's problem with EVERYTHING.
"I could be an awesome guitar playing, but I struggle due to training limitations."
"I could be a great Opera singer, but I struggle due to training limitations."
"I could be a great jockey, but I am 6'4"...." Ok, well maybe not everything.
ChatGPT sucks at coding because it's not an AI - it's a big ass word predictor.
I actually think the key here is writing good test suits to ensure AI does the right thing...
Here is the full argument: https://medium.com/@samuel.sperling/software-2-1-ai-is-coding-now-why-test-mastery-is-your-new-job-security-31a65e792f7f
Next-Gen Brain Implant Uses a Graphene Chip
Video friday: robot crash-perches, hugs tree, ieee learning network celebrates five years, related stories, what to do when the ghost in the machine is you, chatgpt’s new upgrade teases ai’s multimodal future, chatgpt may be a better improviser than you.
New research helps unlock the secrets of flow, an important tool for creative and problem solving tasks
Does it seem like everyone's talking about 'flow', all of a sudden?
Maybe because many people are. Flow has been shown to help those experiencing it become effortlessly absorbed in a creative or problem-solving task, and more resistant to distraction, whether that task be writing, playing sport, conducting surgery or making music.
New research is routinely emerging extolling the virtues of the seemingly-elusive mental state, and its enormous potential for creativity and performance.
A recent study out of Drexel University's Creative Research Lab in Philadelphia, led by Dr. John Kounios, sought to examine the 'neural and psychological correlates of flow' in a sample of jazz guitarists.
Some guitarists were very experienced and some less so, with the study looking at what their brains were up to while they improvised.
Study participants were fitted with EEG (electroencephalogram) electrode caps and their brain activity was monitored while performing an improvisation to a pre-determined chord progression, or jazz 'lead'.
They were then told to self-report their experience of flow. Their performances were subsequently assessed for quality by a panel of musical experts.
According to the study, the participants with the most experience found their flow most easily and also gave the best-rated performances. This was found to be from a combination of established skills and their capacity to 'let go.'
Similarly, the EEGs of the best-performing improvisers showed reduced activity in the superior frontal gyri of their brains. This region is associated with executive control, or conscious decision-making.
Letting go, in this instance, means a relinquishing of conscious control.
What is flow, and how can it help us
Mihalyi Csikszentmihalyi was the psychologist who first identified flow: "a state in which people are so involved in an activity that nothing else seems to matter; the experience is so enjoyable that people will continue to do it even at great cost, for the sheer sake of doing it."
ABC Classic presenter and registered psychologist Greta Bradman breaks down the flow state further:
"Being in flow feels good. You might not even have a sense of time when doing a task, be it washing the dishes or getting into a gnarly work task.
"There's this real sense of having focus or meeting the world in flow."
For people working in highly competitive fields where optimised performance is vital, like music performance, being able to tap into tools like flow can make a huge difference for success.
Dr. Steffen Herff, leader of the Sydney Music, Mind and Body Lab at Sydney University, suggests one way flow might help musicians find that cutting edge.
"One component that makes flow so interesting from a cognitive neuroscience and psychology perspective, is that it comes with a 'loss of self-consciousness'," he says.
The fears and insecurities that come with performing to an audience are pushed from the forefront of the mind.
"In other words, gone are all these pesky thoughts of self-doubt."
The benefits of flow for peak creativity
Herff and his team are continually exploring ways to best support musicians both mentally and physically, with techniques such as biofeedback and mental imagery.
Herff says improvising requires a lot of split-second decisions, alongside high-level creative judgements.
By introducing flow into this process, "all the fears, desires, and anxieties that hold you back are gone, whilst at the same time [you're] able to draw more efficiently from all the hours of practise and experience you have accumulated over the years."
Pianist, composer and improviser Nat Bartsch first heard about flow in her Honours year at the Victorian College of the Arts.
As an artist with autism and ADHD, Bartsch has learnt to deliberately foster ways of creating time and space to find that flow state.
"What I love about this study is that it dispels the myth that artists must always wait for 'inspiration to strike' – to be a professional artist is to be able to switch your creativity on and off, on any given day."
She agrees that experience makes all the difference, particularly when it comes to letting go.
"If you know who you are on the stage, or at your instrument, it's easier to let go and trust in what you'll come up with."
Finding flow by letting go
The study's authors explain that flow requires three conditions: "a balance between challenge and skill, clear, proximate goals, and immediate feedback about progress and performance."
It makes sense, then, that a more experienced player would be able to access these conditions more readily. They've had more time to develop skills, set directions for themselves, and form the capacity to critically analyse their own work. And then, let that go.
While flow is not the only way to develop one's musical improvisation skills, Herff acknowledges that this new research is exciting in showing great potential in helping to clarify the brain processes that determine whether a flow state is achieved.
Kounios is clear that practice makes perfect, but flow is about letting go, leaving those looking to find it with one last piece of advice taken from jazz great Charlie Parker:
"You've got to learn your instrument. Then, you practise, practise, practise. And then, when you finally get up there on the bandstand, forget all that and just wail."
Sign up to the ABC Classic Newsletter
- X (formerly Twitter)
Related Stories
You can use music to change your mood — but there's a catch.
Hitting the high notes: The rich history of jazz at the ABC
There wasn't a jazz club when James Valentine was growing up in Ballarat. Instead he tuned into the ABC
What happened when a concert pianist wore a heart rate monitor during a marathon performance
- Neuroscience
- The University of Sydney
- United States
- Share full article
Advertisement
Subscriber-only Newsletter
Climate Forward
Solving problems with susan solomon.
She played a crucial role in fixing the ozone hole, and has thoughts on climate change.

By Cara Buckley
It’s been an especially intense week, with election-related stress and political divisiveness only increasing. So, it seemed like a good time to hear from someone who has demonstrated how people can come together to fix huge problems and who has also played a crucial role in helping remediate a global threat.
In the 1980s, the groundbreaking atmospheric chemist Susan Solomon pioneered our understanding that the then-gaping hole in the ozone layer over Antarctica was caused by industrial chlorofluorocarbons, or CFCs. A damaged ozone layer increases ultraviolet radiation on Earth, harming humans, ecosystems, plants and animals. Dr. Solomon’s work underpins the Montreal Protocol, which banned 99 percent of ozone-depleting substances. Ratified by every country on the planet, the agreement is reversing the harms done to the ozone layer and is considered one of the most successful environmental treaties in history.
In her latest book, “ Solvable: How We Healed the Earth, and How We Can Do it Again ,” which was published last month, Dr. Solomon, who teaches at M.I.T., argues that we can learn from past environmental fights. Public awareness and consumer pressure can influence lawmakers, she says, and lead to positive change.
Here are excerpts from our interview, edited and condensed for clarity.
Why this book and why now?
People need to have some hope. We imagine that we never solve anything, that we have all these horrific problems and they’re just getting worse and worse and worse. I’m not going to say we don’t have any problems. We do. But it’s really important to go back and look at how much we succeeded in the past and what are the common threads of those successes.
The chemical companies’ pushback to reining in CFCs is arguably minimal compared to resistance from oil and gas companies to reducing greenhouse gas emissions. And the ozone issue didn’t have quite the same fervent political and polarized dissent from the public around it. Are these apples and apples comparisons?
No doubt, climate change is probably the heaviest lift we’ve ever attempted, just because energy is so embedded in the economy. Countries that use more fossil fuel energy are generally richer. There’s almost a linear relationship between how much you emit and how rich you are.
We are having trouble retrieving the article content.
Please enable JavaScript in your browser settings.
Thank you for your patience while we verify access. If you are in Reader mode please exit and log into your Times account, or subscribe for all of The Times.
Thank you for your patience while we verify access.
Already a subscriber? Log in .
Want all of The Times? Subscribe .
More From Forbes
Ai and the municipal bond market: solving the pricing problem.
- Share to Facebook
- Share to Twitter
- Share to Linkedin
Rusty Cash Register
For a brief time, I worked for a pricing service, then Thomson Reuters, now LSEG. I took the job for two reasons. First, a colleague I liked worked there, so it would be fun. Second, after joining the chorus of grumblers about how bad municipal bond pricing was, I was curious for a look behind the curtains.
Ask nearly anyone in the muni market about pricing and they usually respond with words that rhyme with “it pucks”. One rationale is the market has what is genteelly referred to as a ‘structural problem’. In broad terms, the problem is that of the $4 trillion par value outstanding bonds with over 1 million unique identifiers, just 0.33 percent of those traded . That was in 2023—a record trading year. Of bonds that do trade, the market is essentially bifurcated between institutional block sizes ($1 million or larger) or retail odd-lots ($100,000 or smaller).
Hockey Pucks
Institutional block trades drive valuations, with trades generally in big new issue underwritings and on the ‘long end’ of the curve: 20 year and 30 year maturities. In most cases, bonds from new issues trade for a few months, then get laid to rest in a mutual fund or SMA portfolio. It’s what market participants call “going to bond heaven”.
Best High-Yield Savings Accounts Of 2024
Best 5% interest savings accounts of 2024.
Prices on retail odd-lot trades, usually in bonds from 1 and 10-year maturities, are rarely if ever considered in valuations. In part because of that, it’s a woefully inefficient segment of the market. This is peculiar in and of itself, given the ever-increasing record number of trades. Recall that retail odd-lot size of $100,000 and under? In 2023, the average daily customer ‘bought and sold’ par trades in that range was $835.8 million—a 55 percent increase from 2019’s $538.5 million. It looks like 2024 could beat that. But the impact on pricing? Negligible.
[Quick aside. All of the trade and issuance numbers referred to this article can be found in the Municipal Securities Rulemaking Board Factbooks and in the “Market Statistics” links on the MSRB EMMA website .]
The first week at the job confirmed my fears. The pricing methodology was rudimentary, at best. Basically, bonds were priced three ways.
Count to Three
First, direct live trade. If there was a trade, that set the price for that bond and all other of those bonds along the 1 year-to-30-year yield curve.
Second was the “comp trade”. While a bond didn’t have a live trade, other bonds that were comparable—issue size, coupon, structure, maturity, rating, and so forth—had live trades. Those “comp trade” prices set the price on bonds that didn’t trade.
The third, the extrapolated trade, is from where the market’s opaque pricing reputation germinates. Since the vast majority of bond issues are under $100 million—in 2023, it was over 90% of the market , a number that has not varied much over the last decade—most of those are structured with individual maturities under $1 million. Correspondingly, that same vast majority of bonds don’t have and never will have institutional block size trades to get pricing guidance from.
However, any bond held by a regulated investment advisor for a client—mutual fund, SMA, broker/dealer—needs marked-to-market, end-of-day pricing to comply with the “Fair Value” provisions of SEC Rule 2a-5 . But as noted, over 99% of these bonds lack live trades. To solve for this, pricing services create complex matrices to determine those values. Billions of dollars of bonds are priced off of a quantitatively derived educated guess off of what may be stagnant data of varying or indeterminate accuracy.
It’s a methodology, perhaps done in good faith, that generates a value number. But is that value truly a fair market value if the price you see on your brokerage statement isn’t likely to be even close to the price you’ll get if you want to buy or sell that bond?
This is not to suggest that data on bonds that do trade is not readily available and current. The Municipal Securities Rulemaking Board offers a real time trade data subscription. Additionally, the MSRB’s EMMA (“Electronic Municipal Market Access”) offers a price discovery tool , a regularly updated most actively traded bond list , and other price resources on the website. It’s quite impressive.
But for the vast number of bonds just quietly accruing interest, their pricing doesn’t come until the end of the day. There is no up to the second, or even up to the minute pricing on bonds. All this only reinforces the market’s reputation for opaqueness.
Look closely enough at the opacity and one thing does become a bit clearer. Municipal bond pricing, as it is now, is more akin to a big echo chamber: a few trades reverberate throughout the market.
As my days at Thomson wore on, I drifted over to the more intellectually challenging valuations on high yield, distressed, and defaulted bonds. It was a brief stay; I don’t think I lasted a full year before leaving to join the muni fintech startup Neighborly.
Yield to the Curve
As if pricing on individual bonds wasn’t opaque enough, it extends to the yield curve.
Every fixed income market professional tracks the yield curve. The yield curve is comprised of the rates on bonds for each maturity from 1 year to 30 years. In the municipal bond market, the U.S. Treasury yield curve and the tax-exempt AAA yield curve are the two yield curves followed most closely.
As fixed income investments, municipal bond prices are based off of these curves—the “spread”, as it is referred to. Spread is the yield on the bond minus the yield on the municipal triple-A yield curve. For example, if a 10 year maturity bond yield is 3.75% and the same maturity on the triple-A curve is 2.75%, the spread is 100 basis points (each basis point being 1/100 th of 1%).
Which curve is used (and it may be one or both) depends on the circumstances, but either way they are a traditional core component of bond valuation. If interest rates go up or down, it is reflected in the curve. Bond values priced off of the curve are adjusted accordingly. For the municipal curve, there are other considerations as well, such as state tax rates or credit ratings. But for a rule of thumb, if you’re buying or selling a bond, one way to determine a generic price would be to see where the rate on the yield curve is for that bond’s maturity and then pricing the bond off of that.
But here’s the rub: what if you don’t have an accurate, up-to-the-minute yield curve to refer to?
broken road by landslide
Traditionally, the market has turned to Refinitiv’s Municipal Market Monitor (TM3) yield curves if only because there haven’t been many other competitors. Derived from longer maturity AAA state general obligation bonds, the TM3 Municipal AAA MMD has been the market’s long-time but unofficial benchmark. It reflects where institutional buy side (i.e., mutual funds) and sell side (broker/dealers) expect to transact. It is released when something material changes in the market, which is usually three times a day, but the timing can be variable. TM3 has a library of curves for subscribers, boasting some 250 survey-based scales (read: yield curves) across numerous sectors, credit rankings, and other market matrices, many with decades of yield curve data.
But between these postings, investors, underwriters, traders, and anyone else involved in trying to price a bond accurately, are left without an up-to-the-minute benchmark yield curve. Curves other than MMD do exist (you can find those on the MSRB website ) but most are subscription-based and are publicly available only at the end of the day. Not particularly helpful in a fast-moving market situation.
The market needs a solution.
Boots on the Ground
The Tech Cavalry Arrives
Having worked with data scientists and software engineers, I can tell you firsthand that what turns them on the most is a good challenge. The more intractable the problem, the more impossible it seems, the more they are drawn to it. It’s like magnets to iron.
Moreover, they see the old guard of TM3, ICE, and Bloomberg as exposed and vulnerable to newer, faster, and more efficient AI technologies. Combine a multi-trillion dollar pricing problem with the opportunity to upend embedded incumbents? It’s a nearly irresistible tech challenge.
Meet the Startups!
Enter four very eager and AI-driven fintech start-ups fast to use data science, artificial intelligence, and machine learning to tackle the muni market’s pricing and yield curve problem. And that’s four just as of today. It’s likely there will be more.
Open for business
Startup #1: Spline Data
Spline Data creates real-time, model-driven pricing and yield curves for the municipal bond market. Utilizing around 140 metrics from trading and other data, the firm develops cutting-edge statistical analyses to create real-time yield curves and predictive pricing models by applying AI methodologies. Measuring and benchmarking its pricing and curve performance against actual market movements and trade prices, the firm focuses on predicting execution prices—“nowcasting”, not “forecasting”. Backtesting for variances and updating its models accordingly, the firm’s machine learning is always growing and building for greater accuracy.
[Fun Fact: “spline”—with the “i” pronounced as “eye”—is defined as “a piecewise polynomial function used to approximate a smooth curve in a line or surface” or, for those of us who are mere mortals, it is the math applied to a data set to create a continuous and irregular curve , like a Yield Curve.]
Spline’s founder, Matthew Smith, started Spline Data in 2022 after serving as the Head of Trading at Headlands Tech Global Markets, later acquired by TD Securities. The implications of more accurate pricing in a timelier manner will have a waterfall effect throughout the market, contends Smith. Yes, automation is the far-and-away leading benefit of tech and AI integration, but the effects quickly cascade—better relative-value identification, a reduction in lead-time for building algorithms, transaction cost analysis, best execution, tax loss harvesting, portfolio optimization without ever initiating an RFQ. The list goes on…and on.
His dream outcome from all this are tighter bid-ask spreads, better execution in odd-lot trades under $1 million and, in the end, an overall more liquid and efficient market benefiting issuers and investors alike.
He is not alone.
Startup #2: ficc.ai
The principals of ficc.ai (the company’s name is in lowercase) realized that given the size and illiquid nature of the market, no human or group of humans can offer real-time pricing. Hence, the firm is solely focused on providing customers accurate and real-time price evaluations. The solution—AI models, learning from tens of millions of data points—offers accurate real-time pricing for the entire universe of municipal bonds, enabled by the latest advances in machine learning. Applying neural network architecture, these ensemble models are able to learn interactions between subsets of features to provide an accurate price. Along with terms and conditions (TNC) data as well as current trading data for every bond, the firm uses prices of Muni ETFs, changing up to the second and throughout the day, to capture the tone of the market at any given point in time. The firm ingests roughly 1TB of data per day. Consistent backtesting and rigorous analysis to evaluate the accuracy on hundreds of features ensure price accuracy across the entire universe.
Startup #3: SOLVE
SOLVE isn’t exactly a startup (it was founded in 2011), but it sure acts as innovative as one. Through both organic growth and acquisition, the firm positioned itself as a leading market data platform provider for fixed-income securities. Already robust with datasets of real-time bids, offers, covers, and other market information on a variety of fixed income instruments, from corporate bonds to syndicated bank loans, its acquisition of Lumesis in 2022 expanded its reach into the municipal bond market. The beta launch of SOLVE Px™ offers AI-generated predictive trade levels on over 900,000 municipal bonds. As SOLVE Co-Founder Eugene Grinberg put it, the platform seeks to see what the next trade level will be with a goal of minimizing prediction error. From his perspective, besides more realistic and real-time market price information, AI also offers the benefit of objectivity, providing an unbiased projection of the next trade price.
In addition to bond reference data—coupon, maturity, and so forth—the firm extracts hundreds of millions of quotes from both structured trade data and unstructured quote data parsed from electronic messaging between traders. Additionally, with their obligor database (economic and demographic data mapped to the CUSIP level), they will consider utilizing such nonfinancial data points where they provide meaningful insight. Applying proprietary AI methodologies to 300 features, SOLVE parses out valuation drivers and, in as close to real-time as possible, generates bond prices.
Grinberg hopes to increase transparency and reduce unnecessary variability in pricing. Like others, he believes the market doesn't operate in a fair and transparent fashion. Applying data and AI, Solve seeks is to level the playing field between institutional and retail investors.
Startup #4: 7 Chord
7 Chord is the newest entrant to the municipal bond pricing universe. Based on her 20-years of credit trading and market structure experience at Blackrock and other Wall Street behemoths, Kristina Fan saw first-hand that rules-based approaches in bond valuation were too crude and rigid. They often did not produce accurate results, especially during volatile markets. Seeing the pricing problem as a way of turning sci-fi ideas into industry-changing products (her words, not mine) she founded 7 Chord in 2016 with Roy Lowrance, a veteran technologist who at the time ran the Center for Data Science at NYU. With markets evolving with ever increasing speed, 7 Chord believes it is more important than ever that prices of investable assets reflect all the information available up to this moment in time. The firm sees AI’s ability to process vast amounts of data in real-time to create dynamic price adjustments based on current market conditions. The municipal bond market is now targeted in their sights.
Its solution, BondDroid, is essentially an orchestra of over 400 different pricing bots. Each has a unique methodology and, using hundreds of different features, is designed to mimic a certain market persona or regime. Some bots are simple, some very complex, but overall it's these diversification of approaches that feeds an AI engine continuously retraining itself in real-time to produce a market-relevant price estimate. That diversification is particularly necessary in the heterogeneous fixed income markets. Moreover, AI implementation is more flexible than any rules-based method and is faster and more scalable than any human.
In her view, probably the most important positive effect of AI pricing is the emergence of this systematic accuracy measurement methodology, as well as a more precise definition of what the ground truth is with regards to pricing of thinly traded assets. Currently, it’s far from perfect. More work is needed for the industry and the regulators to perfect and adopt these methods more broadly.
The royal we agree to all of the above.
The Future was Yesterday
With all this predictive analytics, real-time pricing, yield curves, and spreads, the prediction soon becomes the reality. If you’re sitting on your trading desk and you have a solid idea at what level the next trade is coming, you’re not bidding or asking at the existing trade, you’re bidding or asking at the anticipated trade price. In fact, you’re not human. You’re likely a computer algorithm that is being trained by a neural network to trade against other computers also being trained by a neural network.
Sounds vaguely like a movie I saw back in the ‘80s.
The next article in the AI and the Municipal Bond Market series will cover fundamental credit analysis. With AI, is it even relevant? Or can AI prove its relevance?

- Editorial Standards
- Reprints & Permissions
Join The Conversation
One Community. Many Voices. Create a free account to share your thoughts.
Forbes Community Guidelines
Our community is about connecting people through open and thoughtful conversations. We want our readers to share their views and exchange ideas and facts in a safe space.
In order to do so, please follow the posting rules in our site's Terms of Service. We've summarized some of those key rules below. Simply put, keep it civil.
Your post will be rejected if we notice that it seems to contain:
- False or intentionally out-of-context or misleading information
- Insults, profanity, incoherent, obscene or inflammatory language or threats of any kind
- Attacks on the identity of other commenters or the article's author
- Content that otherwise violates our site's terms.
User accounts will be blocked if we notice or believe that users are engaged in:
- Continuous attempts to re-post comments that have been previously moderated/rejected
- Racist, sexist, homophobic or other discriminatory comments
- Attempts or tactics that put the site security at risk
- Actions that otherwise violate our site's terms.
So, how can you be a power user?
- Stay on topic and share your insights
- Feel free to be clear and thoughtful to get your point across
- ‘Like’ or ‘Dislike’ to show your point of view.
- Protect your community.
- Use the report tool to alert us when someone breaks the rules.
Thanks for reading our community guidelines. Please read the full list of posting rules found in our site's Terms of Service.
ChatGPT: Disruptive or Constructive?
Thursday, Jul 18, 2024 • Jeremiah Valentine : [email protected]
What is Chat GPT?
ChatGPT is a popular emerging technology using Artificial Intelligence. GPT stands for Generative Pre-trained Transformer, which describes an AI program that looks for patterns in language and data learning to predict the next word in a sentence or the next paragraph in an essay. The website has a friendly interface that allows users to interact with AI in a n efficient conversational tone . ChatGPT provides another opportunity for students, instructors, researchers, workers, and others to find practical solutions to everyday and complicated problems.
At the root of this conversation is Artificial Intelligence. I plan to explore applicable uses of AI and ChatGPT in the classroom , entrepreneurial potential uses, and applications in industry .

Everyday Uses of Artificial Intelligence
The use of Artificial I ntelligence varies based on the user and their end goal. While many individuals will use certain programs or websites to meet specific objectives , many companies and apps have begun to utilize this emerging technology to better meet their customer's needs.
Duolingo is a popular foreign language learning application that I use to supplement my Spanish studies . The app uses Artificial Intelligence to assess users' knowledge and understanding as they interact with the program , thus streamlining users learning outcomes.
As another example, Khan Academy is a free online resource that helps teachers and students learn any level of math or other grade school topics for free. They have created Khanmigo , using AI. The model acts as a tutor that helps work through a problem while not directly providing the answer. It can assist in writing an essay or solving a complex math problem step by step.
These everyday applications continue a trend of companies implementing this new technolog y into students and teachers' lives . . This new AI technology also allows business professionals to enhance aspects of their processes.
Entrepreneurs, A.I. and the Advantages
While AI already provides companies and organizations with new ways to interact with and better support their customers, AI could also provide emerging industries and entrepreneurs with new paths to business success.
According to Entrpreneur.com, most businesses currently use AI for customer service purposes , however , AI could also help entrepreneurs create effective spreadsheets cataloging useful data with accuracy that can be incredibly specific or broad. Specifically with customer service, AI can quickly find what a customer needs and solve their problems efficiently. It could also analyze how effective marketing campaigns are influencing customers’ purchases.
As I researched for more information about this topic, I found an article in The Journal of Business Venturing Insights published in March 2023, sharing different techniques business students can use ChatGPT as an asset to generate entrepreneurial business pitches. The article titled “ The Artificially Intelligent Entrepreneur” written by Cole Short, an Assistant Professor of Strategy at Pepperdine University, and Jeremy C. Short, a UTA alumni and Professor at the University of North Texas at Denton, showcased different elevator pitch scenarios.
Students and entrepreneurs study CEOs who have impacted an industry dynamically; the CEO's mentality is an asset . I had the opportunity to question Dr. Jeremy Short on how he arrived at the initial question of using AI as a CEO archetype business consultant. An archetype is a symbol, term, or pattern of behavior which others have replicated or emulated.
He responded, “ We used this existing framework and selected a CEO from each archetype and used ChatGPT to create elevator pitches, social media pitches, and crowdfunding pitches. The strength of ChatGPT is based largely on the creativity of the prompt, which is where we aim as authors.”

CEO Archetypes and Prompt Engineering
ChatGPT allows the user to understand the archetypes of successful CEOs and collaborate with entrepreneurial styles. These archetypes are accessible options to consult with AI. Let ’ s break down different CEO archetypes students used during this study:
Creator CEOs are typically serial entrepreneurs and serve during the growth stages of developing new businesses. These individuals are risk takers recognizing opportunities that others don ’ t see. Elon Musk, CEO of Tesla, SpaceX, and Twitter is the creator archetype.
Transformer CEOs are created by climbing the ladder of a successful business and adding new ideas . They have a firm understanding of the company's culture and work to dramatically change the company, separating it from missteps in the past. Indra Nooyi CEO of PepsiCo is the transformer archetype.
Savior CEOs rescue businesses on the verge of failure with disciplined actions, unique experience and insights they forge a successful path forward for declining businesses. Lisa Su, CEO of AMD is the savior archetype.
ChatGPT was prompted to write an elevator pitch in the style of the previously listed CEOs.
The response for Elon Musk included language about “ building” a product with “ cutting-edge technology.”
Indra Nooyi ’s response included phrases like “ the world is changing” and making “ a positive impact in the world.”
Lisa Su's response produced a pitch speaking about being “ accountable, tough and disciplined” with an emphasis on “ a strong focus on efficiency and performance.”
However, I believe these positions can help entrepreneurs develop their own successful business practices; creating a product your former employer could use to gain an advantage over the competition is disruptive. B uying a company on the brink of bankruptcy that has been mismanaged is a scenario entrepreneurs have explored and practiced .
Prompt engineering is the description of a task AI can accomplish , with instructions embedded in the input. Using prompt engineering, users can fine-tune their input to achieve a desired output incorporating a task description to guide the AI model.
Conversation around ChatGPT and Artificial Intelligence
I asked Dr. Short about how students could use this technology as an asset that guides their learning and, additionally, how instructors can use this as well. He spoke about an assignment he is currently using in his classes. “ Chat GPT might be valuable in helping create a recipe for material that students can then refine. For example, in my social entrepreneurship class students create crowdfunding campaigns for either DonorsChoose , a platform that caters to public school teachers or GoFundMe , a service which allows a variety of project types to a larger userbase . I plan on students using ChatGPT to create a ‘rough draft’ to show me so I can see how they refine their responses for their particular campaigns this upcoming fall.” Th is approach allows students to take advantage of popular technology in a constructive way.
The journal article provided some notable conclusions about ChatGPT , i ncluding “ quality control is essential when using automated tools; a hallmark of success for large language models is their vast associative memory, this strength can also be a weakness. Specifically, models such as OpenAI’s GPT-3.5 and GPT-4 are capable of confidently generating “ hallucinated” output that appears correct but, it is incorrect or completely fabricated. ChatGPT serves as an emerging tool that can efficiently and flexibly produce a range of narrative content for entrepreneurs and serve to inspire future research at the intersection of entrepreneurship and AI.” ChatGPT ’s limitations and potential applications are continually being explored.
Industry Application
After researching various applications of AI, I spoke with Dr. George Benson, Professor and Department Chair of the Department of Management at The University of Texas at Arlington, about AI and ChatGPT from an industry perspective. His research focuses on Artificial Intelligence with Human Resource Management .
Dr. Benson told me that Artificial Intelligence is being invested heavily by human resource departments who are looking to automate hiring practices. Specifically, he mentioned “ HR is using this as a market opportunity. AI is a useful tool to sift through potential applicants by scanning their resumes for qualifications and experiences. Allowing professionals to hire applicants faster.”
This application allows the technology to handle low-level tasks, but the results generated are being handed to a human to review and act on. He spoke about the potential of A.I. “ There are a lot of unknowns, but the technology is new and getting better.” Looking towards the future, technology is already being applied in different ways . These applications are being explored in the classrooms of UTA as well.

Exploration of AI at UTA
The College of Business conduct ed a survey to understand the faculty’s attitude towards A I in the classroom. It was a part of the “Teaching with Chat GPT” workshop on Friday February 9 th , which focus ed on how to integrate Chat GPT and other AI platforms into teaching .
Dr. Kevin Carr, a Clinical Assistant Professor of Marketing at UTA, was a part of the workshop ; he currently teaches Advanced Business Communication . I talked to him about the purpose of the workshop and what he hopes to gain from the group's sessions.
Dr. Carr explained "The point of the workshop is designed to give faculty ideas for instruction and to develop classroom activities to work with students . Our goal for th e workshop is to introduce Artificial Intelligence as a teaching tool for faculty, including showing what AI can do potentially in the classroom. We are going to be very open to faculty’s direction, in terms of ongoing discu ssions and meetings.”
Personal Take
Artificial Intelligence or Chat GPT , in my view, is another useful tool in the toolbox of technology. It will take the air out of certain industries, and it will change jobs, yet every major technological advancement has the potential to do so. The automobile was considered radical, the use of plastic, computers in the workplace, and alternative energy have been impactful on society.
Alternative energy was headlined as the end of oil use. The automobile changed the way cities were formed and led to the creation of a national highway system. Society has always found a way to adapt and overcome major technological innovations, artificial intelligence is not any different.
AI is the technology of tomorrow. It reminds me of something Dr. George Benson said , “ It's cool software that is a sophisticated search engine.” Google, one of the most popular search engines, reshaped the internet, as you search for resources, it is a natural starting point. AI and ChatGPT are an evolution, for students it is a tremendous resource consulting a CEO archetype, creating business pitches, and most importantly shaping the future .

News & Events
- College of Business News
- The Business Maverick
- Business Week

Move fast, think slow: How financial services can strike a balance with GenAI

Take on Tomorrow @ the World Economic Forum in Davos: Energy demand

Perspectives from the Global Entertainment & Media Outlook 2024–2028

Climate risk, resilience and adaptation

Business transformation

Sustainability assurance

The Leadership Agenda

Global Workforce Hopes and Fears Survey 2024

The s+b digital issue: Corporate “power changers”

The New Equation

PwC’s Global Annual Review

Committing to Net Zero

The Solvers Challenge
Loading Results
No Match Found
Purpose, values and behaviours
Our purpose grounds our existence. Our values guide our actions. Our behaviours are how we bring it to life.
Our purpose is to build trust in society and solve important problems.
In an increasingly complex world, we help intricate systems function, adapt and evolve so they can deliver sustained outcomes for communities and society – whether they are capital markets, tax systems or the economic systems within which business and society exist.
Creating a common purpose will help to steer business through the next stage of evolution, as the systems upon which economies and societies depend are disrupted and evolve.
Our why | Purpose
Playback of this video is not currently available
Our how | Values
Our values guide our actions..
While we come from different backgrounds and cultures, our values are what we have in common. They describe the expectations our clients should have of us, describe how we work with each other, and hold us accountable to do our best. They guide our actions and enable our success.
Our five values set the context in which we strive to fulfil our purpose.
What do these values mean in practice?
When working with our clients and colleagues to build trust in society and solve important problems, we...
The PwC Professional | Our behaviours
Our behaviours define how we bring our purpose, strategy and values to life.
When you consider the expectations of our clients, our people and society, one thing is clear: we must evolve to keep pace with the needs of a rapidly changing world. Doing so requires new skills, new ways of thinking, and new capabilities that are consistent across our network. We need a different way to lead and deliver value. And we must begin with integrity.
Trusted Leadership and Distinctive Outcomes are how we deliver on our purpose and strategy, serving our clients and living our values in every interaction, everyday. Guided by Trusted Leadership and Distinctive Outcomes, we'll work to create a better tomorrow.
At PwC we believe it is our obligation - and our opportunity - to take the lead and work together for a better tomorrow. This means our purpose, strategy, and values working as a system: Our purpose grounds our existence. Our strategy directs our focus. Our values guide our actions. And the PwC Professional describes how we behave to bring it to life. And when we behave in this way, we unlock the full potential of our global network. We become an unrivalled place to work and solve together for our clients and society.
Our Code of Conduct
The trust that our clients, our communities and our people place in PwC, and our high standards of ethical behaviour, are fundamental to everything we do. Our purpose, values and behaviours underpin our Code of Conduct which is our frame of reference for the decisions we make every day. It's how we do business.
PwC’s Code of Conduct
Explore the code of conduct, related content, 2023 pwc network environment report.
The 2023 PwC Network Environment Report discusses how PwC is executing its global environment strategy to create a more sustainable future together.
Reporting on our impact - Global Transparency Report 2023
Welcome to our 2023 Global Transparency Report. Explore our financial performance, commitment to quality, risk management, and governance approach at PwC.
Global Annual Review 2023
Explore our Global Annual Review 2023 where we share how over 360,000 PwC people have helped to solve important challenges this year.
Corporate sustainability
PwC Corporate Sustainability. Providing solutions for positive change in society.

Global Corporate Sustainability Leader, PricewaterhouseCoopers International Limited

Bethan Grillo
Managing Director, Global Corporate Sustainability, PricewaterhouseCoopers International Limited

© 2017 - 2024 PwC. All rights reserved. PwC refers to the PwC network and/or one or more of its member firms, each of which is a separate legal entity. Please see www.pwc.com/structure for further details.
- Legal notices
- Cookie policy
- Legal disclaimer
- Terms and conditions
We've detected unusual activity from your computer network
To continue, please click the box below to let us know you're not a robot.
Why did this happen?
Please make sure your browser supports JavaScript and cookies and that you are not blocking them from loading. For more information you can review our Terms of Service and Cookie Policy .
For inquiries related to this message please contact our support team and provide the reference ID below.
Try AI-powered search
- How do you solve a problem like Joe Biden?
The uproar over his candidacy reveals dysfunction afflicting both major parties

Your browser does not support the <audio> element.
I t is as though a giant trap has sprung: Democrats suddenly find themselves faced with the prospect of losing the White House and both houses of Congress just as the Supreme Court’s conservative majority has further empowered the presidency and hobbled the administrative state. Democrats’ scorn for Republicans at choosing an unpopular nominee for president, a candidate compromised by criminality and extremism, has turned to panic as they realise they may have committed to a nominee even more compromised in the eyes of voters, by infirmity. How did the party get itself into this mess? How can it fix things?
The answers are it didn’t and it can’t—at least not in the short term. Indeed, these are trick questions, because they imply that a major party is capable of making independent decisions. Leaders of both parties long ago surrendered any decisive role in choosing nominees, which is why Donald Trump could conduct what his son-in-law, Jared Kushner, called “a full hostile takeover of the Republican Party”. Since President Joe Biden sabotaged his candidacy in a fateful debate, the Democrats have revealed a comparable vulnerability: they cannot co-ordinate their various power centres in Congress and state governments to provide a clear vote of confidence, or no-confidence, in their candidate. “ The signals are way way way more inefficient than most of us thought, and I thought they were pretty inefficient to start with,” says Daniel Schlozman, a political scientist and the author, with Sam Rosenfeld, of “The Hollow Parties”, a new book on the parties’ decline.
That decline dates to the 19th century, but it accelerated in the 1970s with reforms meant to diminish the influence of party bosses, as well as changes to campaign-finance laws. These led donors to shift their giving from the parties to candidates and to new, often shadowy groups that advocated for particular issues or politicians. By 2020, candidates’ campaigns and outside groups—connected to the parties only loosely, if at all—were spending three times as much as the national parties.
Amid the entropy Republicans have proved more directed, in part because wresting control of the courts gave them a strategic focus. That goal drew together the outside groups and officeholders, unifying social conservatives bent on outlawing abortion with corporate conservatives bent on deregulation. Their efforts have not just been aimed at the federal bench. Democrats dominated state Supreme Courts into the 1990s, but since 2013 Republicans have accounted for a majority of the state justices nationwide. It is no coincidence that, as Americans have polarised and sorted themselves geographically by party, Republicans have also done a better job of locking up state elective offices. Of states where one party controls the governor’s office and both houses of the assembly, Republicans dominate 23, Democrats 17. Democrats have all but stopped competing in some rural states , conceding a head start to the Republicans in the Senate and electoral college.
Both parties have become weaker because of the well-intentioned reforms of the 1970s. Once upon a time, party insiders picked nominees. But after their divisive convention in 1968, Democrats instituted reforms, later adopted by the Republicans, to choose nominees only by means of statewide primaries. Now, “robot” delegates to conventions vote mechanically for whoever carried their state. The noble objective was to democratise the process, but it neglected a couple of considerations: a party apparatus without influence over the choice of leader has little influence over anything else; and party insiders, whatever their flaws, are particularly astute judges of fellow politicians.
“The two parties gave up their most important mission, which is the selection of the nominee, and they gave it up to primary voters in an age when whims can win,” says Elaine Kamarck, a member of the Democrats’ governing body, the Democratic National Committee ( DNC ), and the author of “Primary Politics”. “What’s absolutely clear in the case of both Trump and Biden is that it’s important to have people in place who actually know the candidate and know something about governing.” The alternative, she warns, is that “we could subject ourselves to a bunch of charlatans and authoritarians for the next decades.”
Party all the time
Ms Kamarck proposes a system of “peer review” whereby, before the primaries, each party’s congressional representatives and national-committee members would privately question candidates and issue votes of confidence or no-confidence to help guide primary voters. Another fix might be for the Democrats to restore and even enhance the power of “superdelegates”, a group that includes governors, members of Congress and other party eminences. Such delegates are not bound to vote for any candidate, but a Democratic rule from 2018 bars them from casting votes unless the contest goes to a second round of balloting—a virtual impossibility. If Republicans had comparable numbers of superdelegates who could vote in the first round, they might have stopped Mr Trump in 2016, since he arrived at the convention with a slender majority in delegates and considerable opposition.
Fixing the Democrats’ deeper problems would require nurturing local networks of activists across the country year in and year out, rather than leaping quadrennially to the service of that season’s champion in a handful of swing states. When Howard Dean, a former presidential candidate, was elected chairman of the DNC in 2005, he invested in a “50-state strategy” to run Democrats at every level of government in every state. But once he was replaced the party drifted from that ambition. “They paid lip service to that, but they didn’t invest in places like Texas and Mississippi,” Mr Dean says. “And when you don’t do that, you get the result that you’ve got. And it’s getting worse, by the way.” ■
Stay on top of American politics with The US in brief , our daily newsletter with fast analysis of the most important electoral stories, and Checks and Balance , a weekly note from our Lexington columnist that examines the state of American democracy and the issues that matter to voters.
Explore more
This article appeared in the United States section of the print edition under the headline “How do you solve a problem like Joe Biden?”
United States July 13th 2024
- Joe Biden is failing to silence calls that he step aside
- Anguish about Joe Biden’s candidacy is rational, polls suggest
- The Republicans’ policy platform previews the coming campaign
- Meet a leading Trump vice-presidential contender
- Las Vegas’s power couple says goodbye to power

From the July 13th 2024 edition
Discover stories from this section and more in the list of contents
More from United States

Usha Vance, wife of Donald Trump’s VP pick, was once a Democrat
The lawyer, whose parents are Indian immigrants, seems to prioritise ambition

Donald Trump tries to be both unifier and pugilist in his convention speech
The candidate thrills his party but mixes his message

Why MAGA is the future, not just present, of the GOP
The selection of J.D. Vance means that Donald Trump’s influence may linger
Calling Donald Trump a threat to the rule of law has backfired
It strengthened him politically and led to constitutional protections for presidents, not citizens
The Trump shooting has made a mockery of the Secret Service
Protecting presidents requires communication, not just lots of men with guns
Bob Menendez is found guilty of corruption
From head of the Senate Foreign Relations Committee to convicted foreign agent
- Skip to main content
- Keyboard shortcuts for audio player
What we know about the computer update glitch disrupting systems around the world

Bobby Allyn

Bill Chappell
Fatima Al-Kassab

Microsoft, which hosts cloud services with businesses and governments, said it was grappling with service outages after a glitch triggered by software distributed by cybersecurity firm CrowdStrike. Haven Daley/AP hide caption
A technological meltdown left employees of airlines, banks, hospitals and emergency services around the world staring at the dreaded “blue screen of death” on Friday as their computers went inert in what is being described as a historic outage.
“This is basically what we were all worried about with Y2K, except it's actually happened this time,” internet security analyst Troy Hunt said via X .

Security experts race to fix critical software flaw threatening industries worldwide
From continent to continent, Microsoft users reported being suddenly knocked offline, and the culprit was determined to be cybersecurity company CrowdStrike, which says one of its routine software updates malfunctioned.
“CrowdStrike is actively working with customers impacted by a defect found in a single content update for Windows hosts,” the company said in a statement.
Customers using Mac and Linux operating systems were not affected, CrowdStrike said.
When the faulty update crashed computer systems, scores of airport travelers were stranded, hospital appointments were delayed and live news broadcasts were cut short.
How big is the outage?
It is massive, far-reaching and sudden.
Some computer problems cascade, creating ripples of failures. But in this case, the flaw permeated Microsoft systems worldwide nearly immediately. The company says its Windows 365 Cloud PCs, apps and services were affected.
Microsoft remains the dominant desktop operating system worldwide, with more than 72% market share, according to the Statcounter website . The CrowdStrike problem does not directly affect all of those machines: its security software is mainly used by businesses and large organizations. The company says its customers include 43 U.S. states and nearly 300 companies in the Fortune 500.
Hundreds of thousands of Microsoft outages were reported on Friday, according to Downdetector , the website that tracks outages based on users’ reports.
In 16 hours, 311,000 global outage reports came in, Michelle Badrian, senior communications manager at Ookla, which owns Downdetector, told NPR. Of that figure, she added, 58,000 reports were from the U.S., 26,000 from the U.K., and 20,000 from India. Large numbers of reports also came in from Germany, Canada and Australia.
There are signs that relief is on the way: Badrian said that as of midday Friday ET, “we are observing report volumes declining both for Microsoft services and for all services overall.”
While server-related outages are common, the scale of the CrowdStrike disruption was astonishing to many tech observers.
“This IT outage is a stark reminder of how dependent we are on technology and many other things that happen behind the scenes that most of us are unaware of,” said Louisville-based tech executive Adam Robinson on X . “Modern society and the many comforts we enjoy is a fragile thing.”

Passengers wait in front of check-in counters at the capital's Berlin Brandenburg Airport, in Schönefeld, Germany, on Friday after a widespread technology outage disrupted flights, banks, media outlets and companies around the world. Christoph Soeder/AP/DPA hide caption
What about air travel?
More than 2,000 flights originating or landing in the U.S. were canceled as of noon ET Friday, and more than twice that number were delayed, according to the FlightAware tracking site.
Delta Airlines, United Airlines and American Airlines announced they were resuming some or all of their scheduled flights after initially being grounded when the problem struck their systems. The airlines also said they were issuing waivers to affected customers.
Amsterdam’s Schiphol Airport — a major hub for long-distance flights — said a "global system failure" impacted incoming and outgoing flights on one of the busiest days of the year.
Landings at Zurich airport were suspended and flights in Hungary disrupted.
Spanish airport operator Aena reported a computer systems “incident” at all Spanish airports that it said could cause delays.
What other kinds of services went offline?
In some states, including Alaska and Ohio , 911 phone lines were down.
The U.K.’s National Health Service has been widely affected. The NHS said Friday that doctors’ appointments and patient records had been affected but that there was no known impact on emergency services. The BBC reported that two-thirds of doctors’ practices in Northern Ireland had been affected, with doctors unable to access patient records, generate prescriptions or see the result of laboratory tests.
In Germany, some hospitals canceled non-emergency operations.
Broadcasters around the world were also affected. In France and Australia , live television broadcasts were knocked offline.
Sky News, a major U.K. news channel, was off air for a time on Friday morning. It later returned, but without “ full capabilities , ” its chairman, David Rhodes, said on X Friday afternoon. A post on Australia’s ABC News website said the broadcaster was experiencing a “major network outage.”
The London Stock Exchange’s news service stopped working. Shipping in the Baltic was also impacted, with the container hub of Gdansk in Poland hit by major disruptions.
How do people fix their computers?
CrowdStrike says the problem was not a cyberattack, but rather a software glitch. The company said that after identifying the issue, it withdrew the "problematic channel file" that was affecting customers' systems.
Because of that move, if a Windows system with CrowdStrike's Falcon sensor was brought online after 1:27 a.m. ET Friday , the company said, it wouldn't be affected.
It also published a workaround that involves booting a Windows machine in a recovery environment, deleting a single file in the CrowdStrike directory, and restarting.

An airport information screen displays an error message rather than travel information at San Francisco International Airport on Friday after a computer problem unraveled systems in the U.S. and dozens of other countries. Talia Smith/NPR hide caption
What is CrowdStrike?
It’s a U.S. cybersecurity firm based in Austin, Texas. The company went public in 2019 and is currently in the S&P 500 index. As of early July, CrowdStrike’s stock had been riding months of gains. But share prices fell sharply in early trading Friday.
“This is clearly a major black eye for CrowdStrike,” said WedBush analyst Dan Ives.
CrowdStrike made headlines in 2016, when the company was hired by the Democratic National Committee to investigate a breach of its data systems . CrowdStrike determined that the hack was a case of foreign interference — the work of Russian-backed hacking groups.
The company’s marquee product is its “Falcon” cybersecurity software — and it traced the current problem to a change in a sensor in that system. That also helps explain how and why the resulting failures might have spread so quickly: Rather than being stored locally, the Falcon security platform “is 100% cloud-based.”
The company apologized for the outages on Friday, stating, "We understand the gravity of the situation and are deeply sorry for the inconvenience and disruption."
This is a developing story and will be updated.

IMAGES
VIDEO
COMMENTS
And third, pay attention to how you're feeling. Embracing complexity means learning to better manage tough emotions like fear and anger. The problems we're facing often seem as complex as they ...
Step 1: Identify the Problem. The problem-solving process starts with identifying the problem. This step involves understanding the issue's nature, its scope, and its impact. Once the problem is clearly defined, it sets the foundation for finding effective solutions.
A synthesis definition. By pulling the main themes of these definitions together, we can get a sense of what complex problem-solvers must do: Gain a better understanding of the phenomena of a complex problem or mess. Use a discipline-agnostic approach in order to develop deliberate interventions.
Here are some more detailed steps you can follow to help solve complex problems: Define the problem clearly: The first step in solving any problem is to define it clearly and understand exactly what you are trying to solve. Gather all the necessary information and identify the root cause of the problem. This may involve conducting research ...
Collaborate with Others. Collaborating with others can help you develop your complex problem-solving skills. Working in a team environment can expose you to new ideas and approaches, help you identify blind spots, and provide opportunities for feedback and support. 5. Seek Out Challenging Problems.
Breaking Down Complex Math Problems: A Step-by-Step Guide. Understanding complex math problems is essential for students, teachers, and individuals keen on applying math in daily life or at work. Here's a step-by-step guide to help you dissect and tackle these seemingly daunting equations or problems. Step 1: Understand the Problem
Complex problem solving is a series of observations and informed decisions used to find and implement a solution to a problem. Beyond finding and implementing a solution, complex problem solving also involves considering future changes to circumstance, resources and capabilities that may affect the trajectory of the process and success of the ...
Step 5: Going Deeper into the Issues. After defining the problem and the system structure, this step tends to understand the underlying problems through clarifying four items: the purpose of the system (what we want), the mental models, the large system, and personal role in the situation. Set 6: Plan an Intervention.
Solve Complex Problems by Expanding Your Thinking Too many leaders approach complex problems with either-or thinking: The answer is right or wrong, good or bad, win or lose. To cultivate a nuanced ...
Here are some things you can do to improve your ability to solve complex problems: 1. Always be learning. Prepare your mind to be a bit faster and deal with things in a better way by constantly ...
When you reach a good-enough-for-now idea, end the meeting and try it. Often teams reach this point in 30 minutes and then spend the next couple of hours trying to perfect it, because they're ...
This complex problem-solving course introduces participants to MIT's unique, powerful, and integrative System Dynamics approach to assess problems that will not go away and to produce the results they want. Through exercises and simulation models, participants experience the long-term side effects and impacts of decisions and understand the ...
Go to: Computer-simulated scenarios have been part of psychological research on problem solving for more than 40 years. The shift in emphasis from simple toy problems to complex, more real-life oriented problems has been accompanied by discussions about the best ways to assess the process of solving complex problems.
All episodes. Details. Transcript. December 04, 2018. Corey Phelps, a strategy professor at McGill University, says great problem solvers are hard to find. Even seasoned professionals at the ...
Approach and solve large and complex problems. Assess end-to-end processes and associated challenges, in order to significantly increase the likelihood of success in developing more complex systems. Implement effective problem-solving techniques, including abstracting the problem, idea generation, concept development and refinement, system ...
Complex problem-solving (CPS) refers to the cognitive processes humans use when reaching a solution to a complex problem. It requires much more than applying acquired skills or knowledge to help solve a challenge. CPS doesn't offer a clear path from the problem to the solution, so it's been the subject of psychological research since the late ...
Regardless of topic, the students in a section of Solving Complex Problems all work together in the first few class sessions to predict what challenges will arise and to parse the overall problem into a series of 5 to 10 themes. For example, themes might include the environmental context of the problem, engineering challenges, public relations ...
7 sample answers to "Describe a time when you have a simple solution to a complex problem.". I remember such a situation from my last engineering job. Facing a tricky app development task, a team of developers were stuck at one point. They were just adding new layers to the code, making the entire app more robust and complex, which isn't ...
Solving complex problems is one of the most essential, yet poorly understood skills of working in organizations. HEC Paris MBA students Maxine Riley and Mich...
Large Language Models (LLMs) have demonstrated remarkable performance in solving math problems, a hallmark of human intelligence. Despite high success rates on current benchmarks; however, these often feature simple problems with only one or two unknowns, which do not sufficiently challenge their reasoning capacities. This paper introduces a novel benchmark, BeyondX, designed to address these ...
Overall, ChatGPT was fairly good at solving problems in the different coding languages—but especially when attempting to solve coding problems that existed on LeetCode before 2021.
Flow has been shown to help those experiencing it become effortlessly absorbed in a creative or problem-solving task, and more resistant to distraction, whether that task be writing, playing sport ...
Susan Solomon, atmospheric scientist and professor at M.I.T. "No doubt, climate change is probably the heaviest lift we've ever attempted," she said.
Applying data and AI, Solve seeks is to level the playing field between institutional and retail investors. Startup #4: 7 Chord 7 Chord is the newest entrant to the municipal bond pricing universe.
Google is sponsoring a $5 million global XPrize competition to develop quantum computing algorithms to solve current problems in areas including climate, sustainability and health. Nvidia Corp ...
It can assist in writing an essay or solving a complex math problem step by step. These everyday applications continue a trend of companies implementing this new technolog y into students and teachers' lives. . This new AI technology also allows business professionals to enhance aspects of their processes.
Our purpose is to build trust in society and solve important problems. In an increasingly complex world, we help intricate systems function, adapt and evolve so they can deliver sustained outcomes for communities and society - whether they are capital markets, tax systems or the economic systems within which business and society exist.
OpenAI has come up with a set of five levels to track its progress toward building artificial intelligence software capable of outperforming humans, the startup's latest effort to help people ...
How do you solve a problem like Joe Biden? From the July 13th 2024 edition. Discover stories from this section and more in the list of contents. Explore the edition. Share. Reuse this content.
CrowdStrike says the problem was not a cyberattack, but rather a software glitch. The company said that after identifying the issue, it withdrew the "problematic channel file" that was affecting ...