myCBSEguide
- Mathematics
- Case Study Class 10...

Case Study Class 10 Maths Questions
Table of Contents
myCBSEguide App
Download the app to get CBSE Sample Papers 2023-24, NCERT Solutions (Revised), Most Important Questions, Previous Year Question Bank, Mock Tests, and Detailed Notes.
Now, CBSE will ask only subjective questions in class 10 Maths case studies. But if you search over the internet or even check many books, you will get only MCQs in the class 10 Maths case study in the session 2022-23. It is not the correct pattern. Just beware of such misleading websites and books.
We advise you to visit CBSE official website ( cbseacademic.nic.in ) and go through class 10 model question papers . You will find that CBSE is asking only subjective questions under case study in class 10 Maths. We at myCBSEguide helping CBSE students for the past 15 years and are committed to providing the most authentic study material to our students.
Here, myCBSEguide is the only application that has the most relevant and updated study material for CBSE students as per the official curriculum document 2022 – 2023. You can download updated sample papers for class 10 maths .
First of all, we would like to clarify that class 10 maths case study questions are subjective and CBSE will not ask multiple-choice questions in case studies. So, you must download the myCBSEguide app to get updated model question papers having new pattern subjective case study questions for class 10 the mathematics year 2022-23.
Class 10 Maths has the following chapters.
- Real Numbers Case Study Question
- Polynomials Case Study Question
- Pair of Linear Equations in Two Variables Case Study Question
- Quadratic Equations Case Study Question
- Arithmetic Progressions Case Study Question
- Triangles Case Study Question
- Coordinate Geometry Case Study Question
- Introduction to Trigonometry Case Study Question
- Some Applications of Trigonometry Case Study Question
- Circles Case Study Question
- Area Related to Circles Case Study Question
- Surface Areas and Volumes Case Study Question
- Statistics Case Study Question
- Probability Case Study Question
Format of Maths Case-Based Questions
CBSE Class 10 Maths Case Study Questions will have one passage and four questions. As you know, CBSE has introduced Case Study Questions in class 10 and class 12 this year, the annual examination will have case-based questions in almost all major subjects. This article will help you to find sample questions based on case studies and model question papers for CBSE class 10 Board Exams.
Maths Case Study Question Paper 2023
Here is the marks distribution of the CBSE class 10 maths board exam question paper. CBSE may ask case study questions from any of the following chapters. However, Mensuration, statistics, probability and Algebra are some important chapters in this regard.
| I | NUMBER SYSTEMS | 06 |
| II | ALGEBRA | 20 |
| III | COORDINATE GEOMETRY | 06 |
| IV | GEOMETRY | 15 |
| V | TRIGONOMETRY | 12 |
| V | MENSURATION | 10 |
| VI | STATISTICS & PROBABILITY | 11 |
Case Study Question in Mathematics
Here are some examples of case study-based questions for class 10 Mathematics. To get more questions and model question papers for the 2021 examination, download myCBSEguide Mobile App .
Case Study Question – 1
In the month of April to June 2022, the exports of passenger cars from India increased by 26% in the corresponding quarter of 2021–22, as per a report. A car manufacturing company planned to produce 1800 cars in 4th year and 2600 cars in 8th year. Assuming that the production increases uniformly by a fixed number every year.
- Find the production in the 1 st year.
- Find the production in the 12 th year.
- Find the total production in first 10 years. OR In which year the total production will reach to 15000 cars?
Case Study Question – 2
In a GPS, The lines that run east-west are known as lines of latitude, and the lines running north-south are known as lines of longitude. The latitude and the longitude of a place are its coordinates and the distance formula is used to find the distance between two places. The distance between two parallel lines is approximately 150 km. A family from Uttar Pradesh planned a round trip from Lucknow (L) to Puri (P) via Bhuj (B) and Nashik (N) as shown in the given figure below.
- Find the distance between Lucknow (L) to Bhuj(B).
- If Kota (K), internally divide the line segment joining Lucknow (L) to Bhuj (B) into 3 : 2 then find the coordinate of Kota (K).
- Name the type of triangle formed by the places Lucknow (L), Nashik (N) and Puri (P) OR Find a place (point) on the longitude (y-axis) which is equidistant from the points Lucknow (L) and Puri (P).
Case Study Question – 3
- Find the distance PA.
- Find the distance PB
- Find the width AB of the river. OR Find the height BQ if the angle of the elevation from P to Q be 30 o .
Case Study Question – 4
- What is the length of the line segment joining points B and F?
- The centre ‘Z’ of the figure will be the point of intersection of the diagonals of quadrilateral WXOP. Then what are the coordinates of Z?
- What are the coordinates of the point on y axis equidistant from A and G? OR What is the area of area of Trapezium AFGH?
Case Study Question – 5
The school auditorium was to be constructed to accommodate at least 1500 people. The chairs are to be placed in concentric circular arrangement in such a way that each succeeding circular row has 10 seats more than the previous one.
- If the first circular row has 30 seats, how many seats will be there in the 10th row?
- For 1500 seats in the auditorium, how many rows need to be there? OR If 1500 seats are to be arranged in the auditorium, how many seats are still left to be put after 10 th row?
- If there were 17 rows in the auditorium, how many seats will be there in the middle row?
Case Study Question – 6
- Draw a neat labelled figure to show the above situation diagrammatically.
- What is the speed of the plane in km/hr.
More Case Study Questions
We have class 10 maths case study questions in every chapter. You can download them as PDFs from the myCBSEguide App or from our free student dashboard .
As you know CBSE has reduced the syllabus this year, you should be careful while downloading these case study questions from the internet. You may get outdated or irrelevant questions there. It will not only be a waste of time but also lead to confusion.
Here, myCBSEguide is the most authentic learning app for CBSE students that is providing you up to date study material. You can download the myCBSEguide app and get access to 100+ case study questions for class 10 Maths.
How to Solve Case-Based Questions?
Questions based on a given case study are normally taken from real-life situations. These are certainly related to the concepts provided in the textbook but the plot of the question is always based on a day-to-day life problem. There will be all subjective-type questions in the case study. You should answer the case-based questions to the point.
What are Class 10 competency-based questions?
Competency-based questions are questions that are based on real-life situations. Case study questions are a type of competency-based questions. There may be multiple ways to assess the competencies. The case study is assumed to be one of the best methods to evaluate competencies. In class 10 maths, you will find 1-2 case study questions. We advise you to read the passage carefully before answering the questions.
Case Study Questions in Maths Question Paper
CBSE has released new model question papers for annual examinations. myCBSEguide App has also created many model papers based on the new format (reduced syllabus) for the current session and uploaded them to myCBSEguide App. We advise all the students to download the myCBSEguide app and practice case study questions for class 10 maths as much as possible.
Case Studies on CBSE’s Official Website
CBSE has uploaded many case study questions on class 10 maths. You can download them from CBSE Official Website for free. Here you will find around 40-50 case study questions in PDF format for CBSE 10th class.
10 Maths Case Studies in myCBSEguide App
You can also download chapter-wise case study questions for class 10 maths from the myCBSEguide app. These class 10 case-based questions are prepared by our team of expert teachers. We have kept the new reduced syllabus in mind while creating these case-based questions. So, you will get the updated questions only.
Test Generator
Create question paper PDF and online tests with your own name & logo in minutes.
Question Bank, Mock Tests, Exam Papers, NCERT Solutions, Sample Papers, Notes
Related Posts
- CBSE Class 10 Maths Sample Paper 2020-21
- Class 12 Maths Case Study Questions
- CBSE Reduced Syllabus Class 10 (2020-21)
- Class 10 Maths Basic Sample Paper 2024
- How to Revise CBSE Class 10 Maths in 3 Days
- CBSE Practice Papers 2023
- Class 10 Maths Sample Papers 2024
- Competency Based Learning in CBSE Schools
Leave a Comment
Save my name, email, and website in this browser for the next time I comment.
- New QB365-SLMS
- NEET Materials
- JEE Materials
- Banking first yr Materials
- TNPSC Materials
- DIPLOMA COURSE Materials
- 5th Standard Materials
- 1st Standard - CVBHSS Materials
- 2nd Standard - CVBHSS Materials
- 3rd Standard - CVBHSS Materials
- 4th Standard - CVBHSS Materials
- 5th Standard - CVBHSS Materials
- 12th Standard Materials
- 11th Standard Materials
- 10th Standard Materials
- 9th Standard Materials
- 8th Standard Materials
- 7th Standard Materials
- 6th Standard Materials
- 12th Standard CBSE Materials
- 11th Standard CBSE Materials
- 10th Standard CBSE Materials
- 9th Standard CBSE Materials
- 8th Standard CBSE Materials
- 7th Standard CBSE Materials
- 6th Standard CBSE Materials
- Tamilnadu Stateboard
- Scholarship Exams
- Scholarships

CBSE 10th Standard Maths Subject Polynomials Case Study Questions With Solution 2021
By QB365 on 21 May, 2021
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
QB365 - Question Bank Software
10th Standard CBSE
Final Semester - June 2015
Case Study Questions
(ii) The expression of the polynomial represented by the graph is
| -49 | -64 | -36 | -81 |
(iii) Find the value of the polynomial represented by the graph when x = 6.
(iv) The sum of zeroes of the polynomial x 2 + 2x - 3 is
(v) If the sum of zeroes of polynomial at 2 + 5t + 3a is equal to their product, then find the value of a.

(ii) Find the value of \(\alpha\) + \(\beta\) + \(\alpha\) \(\beta\) .
(iii) The value of p(2) is
(iv) If \(\alpha\) and \(\beta\) are zeroes of \(x^{2}+x-2, \text { then } \frac{1}{\alpha}+\frac{1}{\beta}=\)
(v) If sum of zeroes of \(q(x)=k x^{2}+2 x+3 k\) is equal to their product, then k =
(ii) The axis of symmetry of the given parabola is
(iii) The zeroes of the polynomial, represented in the given graph, are
(iv) Which of the following polynomial has -2 and -3 as its zeroes?
| \((a) x^{2}-5 x-5\) | \((b) x^{2}+5 x-6\) | \((c) x^{2}+6 x-5\) | \((d) x^{2}+5 x+6\) |
(v) For what value of 'x', the value of the polynomial \(f(x)=(x-3)^{2}+9 \text { is } 9 ?\)
(ii) What will be the expression of the polynomial given in diagram?
| \((a) x^{2}-6 x+16\) | \((b) -x^{2}+6 x+16\) | \((c) x^{2}+6 x+16\) | \((d) -x^{2}-6 x-16\) |
(iii) What is the value of the polynomial, represented by the graph, when x = 4?
(iv) If the tunnel is represented by x 2 + 3x - 2, then its zeroes are
(v) If one zero is 4 and sum of zeroes is -3, then representation of tunnel as a polynomial is
| \((a) x^{2}-x+24\) | \((b) -x^{2}-3 x+28\) | \((c) x^{2}+x+28\) | \((d) x^{2}-x+28\) |

(ii) The sum of product of zeroes taken two at a time is
(iii) Product of zeroes of polynomial p(x) is
(iv) The value of the polynomial p(x), when x = 4 is
(v) If \(\alpha,\beta,\gamma\) are the zeroes of a polynomial g(x) such that \(\alpha+\beta+\gamma=3, \alpha \beta+\beta \gamma+\gamma \alpha=-16\) and \(\alpha \beta \gamma=-48\) then, g(x) =
*****************************************
Cbse 10th standard maths subject polynomials case study questions with solution 2021 answer keys.
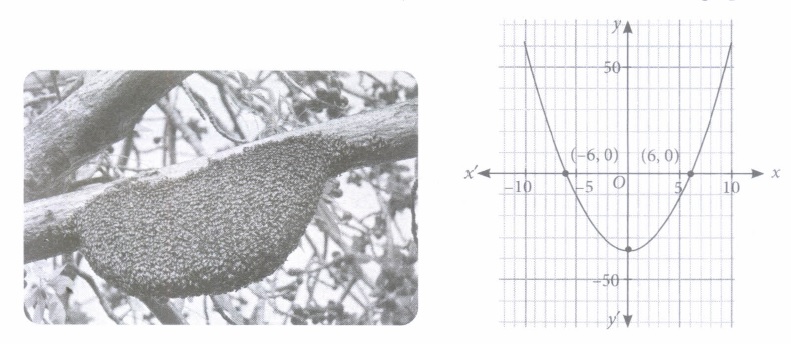
(i) (b): Graph of a quadratic polynomial is a parabolic in shape. (ii) (c): Since the graph of the polynomial cuts the x-axis at (-6,0) and (6, 0). So, the zeroes of polynomial are -6 and 6. \(\therefore\) Required polynomial is p(x) = x 2 - (-6 + 6)x + (-6)(6) = x 2 - 36 (iii) (c) : We have, p(x) = x 2 - 36 Now, p( 6) = 62 - 36 = 36 - 36 = 0 (iv) (b): Letf (x) = x 2 + 2x - 3. Then, \(\text { Sum of zeroes }=-\frac{\text { coefficient of } x}{\text { coefficient of } x^{2}}=-\frac{(2)}{1}=-2\) (v) (d): The given polynomial is at 2 + 5t + 3a Given, sum of zeroes = product of zeroes. \(\Rightarrow \quad \frac{-5}{a}=\frac{3 a}{a} \Rightarrow a=\frac{-5}{3}\)
(i) (b): Given, a and \(\beta\) are the zeroes of \(p(x)=x^{2}-24 x+128\) \(\text { Putting } p(x)=0 \text { , we get }\) \( x^{2}-8 x-16 x+128=0 \) \(\Rightarrow x(x-8)-16(x-8)=0 \) \(\Rightarrow (x-8)(x-16)=0 \Rightarrow x=8 \text { or } x=16 \) \(\therefore \alpha=8, \beta=16\) (ii) (c) : \(\alpha+\beta+\alpha \beta =8+16+(8)(16) =24+128=152 \) (iii) (d) : \(p(2)=2^{2}-2 4(2)+128=4-48+128=84\) (iv) (a): Since a and \(\beta\) are zeroes of \(x^{2}+x-2\) \(\therefore \quad \alpha+\beta=-1 \text { and } \alpha \beta=-2 \) \(\text { Now, } \frac{1}{\alpha}+\frac{1}{\beta}=\frac{\beta+\alpha}{\alpha \beta}=\frac{-1}{-2}=\frac{1}{2}\) (v) (c): Sum of zeroes \(=\frac{-2}{k}\) Product of zeroes \(=\frac{3 k}{k}=3\) According to question, we have \(\frac{-2}{k}=3\) \(\Rightarrow \quad k=\frac{-2}{3}\)
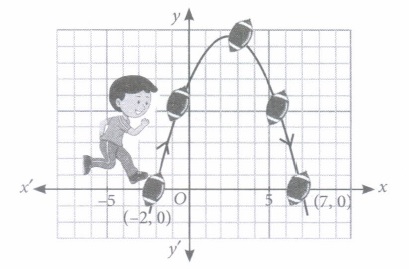
(i) (b): The shape of the path of the soccer ball is a parabola. (ii) (c): The axis of symmetry of the given curve is a line parallel to y-axis. (iii) (a): The zeroes of the polynomial, represented in the given graph, are -2 and 7, since the curve cuts the x-axis at these points. (iv) (d): A polynomial having zeroes -2 and -3 is \(p(x)=x^{2}-(-2-3) x+(-2)(-3)=x^{2}+5 x+6\) (v) (c): We have \(f(x)=(x-3)^{2}+9\) \(\text { Now, } 9=(x-3)^{2}+9 \) \(\Rightarrow(x-3)^{2}=0 \Rightarrow x-3=0 \Rightarrow x=3\)
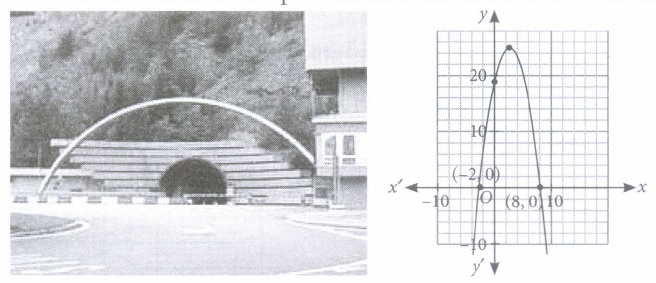
(i) (a): Since, the graph intersects the x-axis at two points, namely x = 8, -2. So, 8, - 2 are the zeroes of the given polynomial. (ii) (b): The expression of the polynomial given in diagram is \(-x^{2}+6 x+16\) (iii) (c) : Let \(p(x)=-x^{2}+6 x+16\) \(\text { When } x=4, p(4)=-4^{2}+6 \times 4+16=24\) (iv) (d): Let \(f(x)=-x^{2}+3 x-2\) Now, consider \(f(x)=0 \Rightarrow-x^{2}+3 x-2=0\) \(\begin{aligned} &\Rightarrow x^{2}-3 x+2=0 \Rightarrow(x-2)(x-1)=0\\ &\Rightarrow x=1,2 \text { are its zeroes. } \end{aligned}\) (v) (b): Let a and \(\beta\) are the zeroes of the required polynomial. Given \(\alpha + \beta = - 3\) If \(\alpha\) = 4, then \(\beta\) = -7 \(\therefore \quad \text { Representation of tunnel is }-x^{2}-3 x+28 \text { . }\)
(i) (c): For finding \(\alpha,\beta,\) \(\gamma\) consider p(x) = 0 \(\Rightarrow \quad x^{3}-18 x^{2}+95 x-150=0 \) \(\Rightarrow \quad(x-3)\left(x^{2}-15 x+50\right)=0 \) \(\Rightarrow \quad(x-3)(x-5)(x-10)=0 \Rightarrow x=10 \text { or } x=5 \text { or } x=3 \) \(\text { Thus } \alpha=10, \beta=5 \text { and } \gamma=3\) (ii) (d): Here \(\alpha=10, \beta=5 \text { and } \gamma=3\) \(\therefore\) Sum of product of zeroes taken two at a time \(\begin{array}{l} =\alpha \beta+\beta \gamma+\gamma \alpha=(10)(5)+(5)(3)+(3)(10) \\ =50+15+30=95 \end{array}\) (iii) (a): Product of zeroes of polynomial p(x) = \(\alpha\beta\gamma\) = (10) (5) (3) = 150 (iv) (b): We have \(p(x)=x^{3}-18 x^{2}+95 x-150\) \(\begin{array}{l} \text { Now, } p(4)=4^{3}-18(4)^{2}+95(4)-150 \\ =64-288+380-150=6 \end{array}\) (v) (d): \(g(x)=x^{3}-(\alpha+\beta+\gamma) x^{2} +(\alpha \beta+\beta \gamma+\gamma \alpha) x-\alpha \beta \gamma \) \(\Rightarrow g(x)=x^{3}-3 x^{2}-16 x-(-48)=x^{3}-3 x^{2}-16 x+48\)
Related 10th Standard CBSE Maths Materials
10th standard cbse syllabus & materials, cbse 10th social science the making of a global world chapter case study question with answers, cbse 10th social science nationalism in india chapter case study question with answers, cbse 10th social science the rise of nationalism in europe chapter case study question with answers, cbse 10th science metals and non metals chapter case study question with answers, cbse 10th science acids, bases and salts chapter case study question with answers, cbse 10th science chemical reactions and equations chapter case study question with answers, class 10th science - our environment case study questions and answers 2022 - 2023, class 10th science - magnetic effects of electric current case study questions and answers 2022 - 2023, class 10th science - electricity case study questions and answers 2022 - 2023, class 10th science - human eye and the colourful world case study questions and answers 2022 - 2023, class 10th science - light reflection and refraction case study questions and answers 2022 - 2023, class 10th science - heredity and evolution case study questions and answers 2022 - 2023, class 10th science - how do organisms reproduce case study questions and answers 2022 - 2023, class 10th science - life processes case study questions and answers 2022 - 2023, class 10th science - periodic classification of elements case study questions and answers 2022 - 2023.

Class VI to XII
Tn state board / cbse, 3000+ q&a's per subject, score high marks.

10th Standard CBSE Study Materials

10th Standard CBSE Subjects

- Class 10 Notes
- 9th IT CODE 402
- 10th IT CODE 402
- 10th Hindi Grammar MCQ
- 9th Hindi Grammar MCQ
Case Study Questions Class 10 Maths with Solutions PDF Download
case study questions class 10 maths pdf, case study questions class 10 maths with solutions, case study questions class 10 maths cbse chapter wise pdf download, how to solve case-based question in maths.
- First of all, a student needs to read the complete passage thoroughly. Then start solving the question
- After reading the question try to understand from which topics the question is asked. and try to remember all the concepts of that topic.
- Sometimes the question is very tricky and you will find it very difficult to understand. In that case, Read the question and passage again and again.
- After solving the answer check your answer with the options given.
- Remember, write only answering your answer book
Link to Download Case-Study Questions of class 10
Post a comment, popular posts.

Communication Skills Class 9 Notes

Information Technology Code 402 Class 10 Solutions

Self Management Skills Class 10 Notes PDF

Introduction to IT and ITes Industry Class 9 Notes

Self Management Skills Class 9 Notes | Employability Skills Unit - 2 Complete Notes

TERM 1 MCQ | Communication Skills Class 10 Questions and Answers

Information Technology Code 402 Class 10 Notes 2023
Menu footer widget.
- Privacy Policy

Top Case-Based Questions: Last Minute Prep for CBSE Class 10 Maths Exam
Cracking case studies: conquer your cbse class 10 maths exam (2023-24 session).
With the CBSE Class 10 board exams just around the corner ( March 11th, 2024 !), many students feel a surge of anxiety, especially when it comes to case-based questions in Maths. The lengthy descriptions can be daunting, making them seem complex. But fear not! Case-based questions are actually a great opportunity to showcase your problem-solving skills, provided your foundational concepts are strong.
This blog post is your one-stop guide to mastering case studies in your upcoming Maths exam. The CBSE board format incorporates 3 case study questions , each worth a total of 4 marks (broken down as 1+1+2). To help you ace these questions, I've compiled a list of practice problems directly from the official CBSE sample papers. By familiarizing yourself with these case studies before the big day, you'll be well-equipped to tackle them with confidence. So, let's dive in and conquer those case studies!
| 10 | |
| CBSE | |
| Mathematics (Standard) | |
| 11/03/2024 | |
| Important Case Based Questions | |
| 2023-24 | |
Also See: 🎯 Class 10 Maths (Standard) Topper's Answer Sheet (2023) ✨
Q. No. 1) Manpreet Kaur is the national record holder for women in the shot-put discipline. Her throw of 18.86m at the Asian Grand Prix in 2017 is the maximum distance for an Indian female athlete. Keeping her as a role model, Sanjitha is determined to earn gold in the Olympics one day.

Initially, her throw reached 7.56m only. Being an athlete in school, she regularly practiced both in the mornings and in the evenings and was able to improve the distance by 9cm every week.
During the special camp for 15 days, she started with 40 throws and every day kept increasing the number of throws by 12 to achieve this remarkable progress.
(i) How many throws Sanjitha practiced on 11th day of the camp?
(ii) What would be Sanjitha’s throw distance at the end of 6 weeks?
When will she be able to achieve a throw of 11.16 m?
(iii) How many throws did she do during the entire camp of 15 days?
Ans. (i) Number of throws during camp. a = 40; d = 12 𝑡 11 = 𝑎 + 10𝑑 = 40 + 10 × 12 = 160 𝑡ℎ𝑟𝑜𝑤𝑠
(ii) a = 7.56 m; d = 9cm = 0.09 m n = 6 weeks t n = a + (n-1)d = 7.56 + 6(0.09) = 7.56 + 0.54 Sanjitha’s throw distance at the end of 6 weeks = 8.1 m
a = 7.56 m; d = 9cm = 0.09 m t n =11.16 m t n = a + (n-1) d 11.16 = 7.56 + (n-1) (0.09) 3.6 = (n-1) (0.09) n-1 = 3.6/0.09 = 40 n = 41 Sanjitha’s will be able to throw 11.16 m in 41 weeks.
(iii) a = 40; d = 12; n = 15 S n = n / 2 [2a + (n-1) d] Sn = 15 / 2 [2(40) + (15-1) (12)] = 15 / 2 [80 + 168] = 15 / 2 [248] =1860 throws
Q. No. 2) Tharunya was thrilled to know that the football tournament is fixed with a monthly timeframe from 20th July to 20th August 2023 and for the first time in the FIFA Women’s World Cup’s history, two nations host in 10 venues. Her father felt that the game can be better understood if the position of players is represented as points on a coordinate plane.
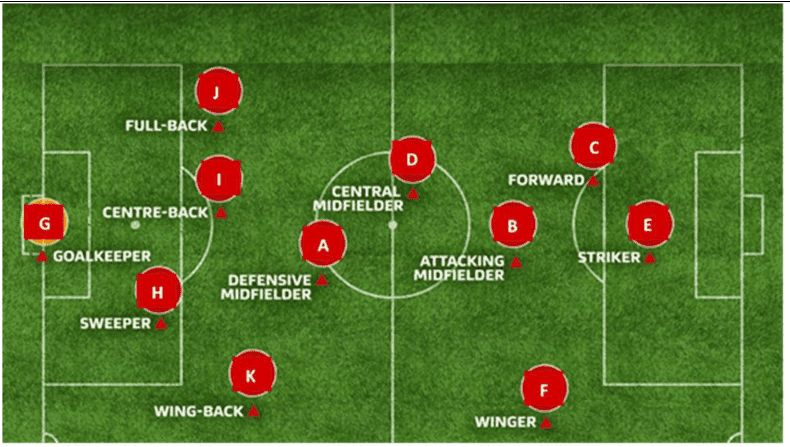
(i) At an instance, the midfielders and forward formed a parallelogram. Find the position of the central midfielder (D) if the position of other players who formed the parallelogram are:- A(1,2), B(4,3) and C(6,6)
(ii) Check if the Goal keeper G(-3,5), Sweeper H(3,1) and Wing-back K(0,3) fall on a same straight line.
Check if the Full-back J(5,-3) and centre-back I(-4,6) are equidistant from forward C(0,1) and if C is the mid-point of IJ.
(iii) If Defensive midfielder A(1,4), Attacking midfielder B(2,-3) and Striker E(a,b) lie on the same straight line and B is equidistant from A and E, find the position of E.
Ans. (i) Let D be (a,b), then
Mid point of AC = Midpoint of BD
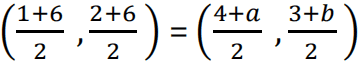
4 + a = 7 and 3+ b = 8
a = 3 and b = 5
Central midfielder is at (3,5)
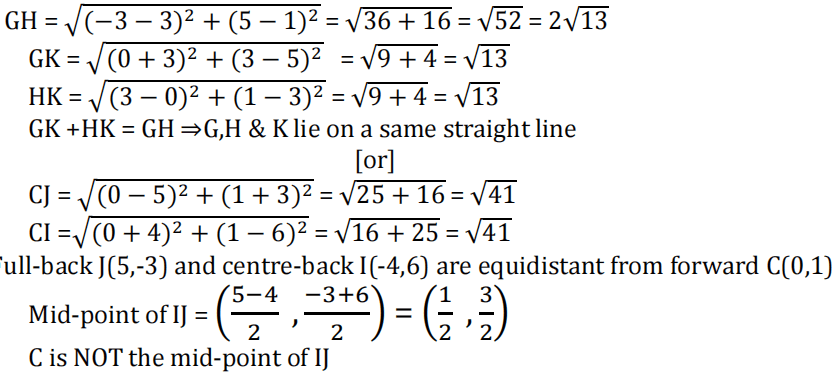
iii. A, B and E lie on the same straight line and B is equidistant from A and E
⇒ B is the mid-point of AE
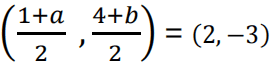
1 + 𝑎 = 4 ; a = 3.
4+b = -6; b = -10
E is (3,-10)
Q. No. 3) One evening, Kaushik was in a park. Children were playing cricket. Birds were singing on a nearby tree of height 80m. He observed a bird on the tree at an angle of elevation of 45°.
When a sixer was hit, a ball flew through the tree frightening the bird to fly away. In 2 seconds, he observed the bird flying at the same height at an angle of elevation of 30° and the ball flying towards him at the same height at an angle of elevation of 60°.
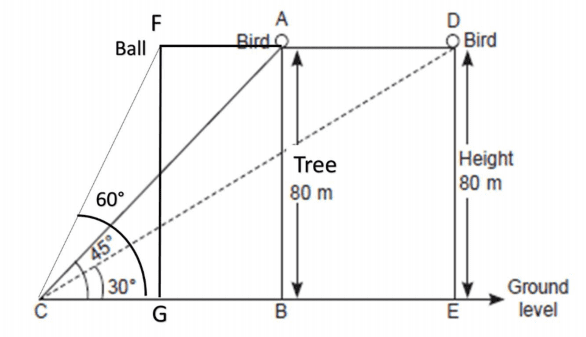
(i) At what distance from the foot of the tree was he observing the bird sitting on the tree?
(ii) How far did the bird fly in the mentioned time?
After hitting the tree, how far did the ball travel in the sky when Kaushik saw the ball?
(iii) What is the speed of the bird in m/min if it had flown 20(√3 + 1) m?
Ans. i. tan 45° = 80/CE
⇒ 1/√3 = 80/CE
⇒ CE = 80√3
Distance the bird flew = AD = BE = CE-CB = 80√3 – 80 = 80(√3 -1) m
tan 60° = 80/CG
⇒ √3 = 80/CG
⇒ CG = 80/√3
Distance the ball travelled after hitting the tree =FA=GB = CB -CG
GB = 80 - 80 / √3 = 80 (1- 1 / √3 ) m
iii. Speed of the bird = distance/time = 20(√3 + 1)/2 m/sec = 10(√3 + 1)m/sec = 10(√3 + 1) x 60 m/min = 600(√3 + 1) m/min
Q. No. 4) An interior designer, Sana, hired two painters, Manan and Bhima to make paintings for her buildings. Both painters were asked to make 50 different paintings each.
The prices quoted by both the painters are given below:
- Manan asked for Rs 6000 for the first painting, and an increment of Rs 200 for each following painting.
- Bhima asked for Rs 4000 for the first painting, and an increment of Rs 400 for each following painting.
(i) How much money did Manan get for his 25th painting? Show your work.
(ii) How much money did Bhima get in all? Show your work.
(iii) If both Manan and Bhima make paintings at the same pace, find the first painting for which Bhima will get more money than Manan. Show your steps.
(iii) Sana's friend, Aarti hired Manan and Bhima to make paintings for her at the same rates as for Sana. Aarti had both painters make the same number of paintings, and paid them the exact same amount in total.
How many paintings did Aarti get each painter to make? Show your work.
Ans. i. Notes that the amounts Manan is paid for each painting forms an AP.
Takes a = 6000, d = 200 and n = 25 to find the amount as
6000 + (25 - 1)200 = Rs 10800.
ii. Finds the total amount earned by Bhima as follows:
S 50 = 50/2 [2(4000) + (50 - 1)(400)]
Solves the above expression to find the total amount as Rs 6,90,000.
iii. Frames equation as follows:
6000 + ( n - 1)200 = 4000 + ( n - 1)400
Solves the above equation to find the value of n as 11 .
Writes that, since they both earn the same amount for the 11th painting, as Bhima's increment is more, Bhima gets more money than Manan for the 12th painting.
Assumes that the number of paintings required is n .
Frames equation as follows:
S n (Manan) = S n (Bhima)
=> 𝑛/2 [2(6000) + ( n -1)200] = 𝑛/2 [2(4000) + ( n -1)400]
Solves the equation from step 1 to find n as 21.
Q. No. 5) In the game of archery, a bow is used to shoot arrows at a target board. The player stands far away from the board and aims the arrow so that it hits the board.
One such board, which is divided into 4 concentric circular sections, is drawn on a coordinate grid as shown. Each section carries different points as shown in the figure. If an arrow lands on the boundary, the inner section points are awarded.
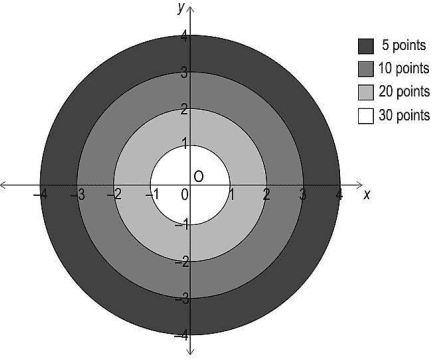
(i) After shooting two arrows, Rohan scored 25 points.
Write one set of coordinates for each arrow that landed on the target.
(ii) If one player's arrow lands on (2, 2.5), how many points will be awarded to the player? Show your work.
(iii) One of Rohan’s arrow landed on (1.2, 1.6). He wants his second arrow to land on the line joining the origin and first arrow such that he gets 10 points for it.
Find one possible pair of coordinates of the second arrow's landing mark. Show your work.
(iii) An arrow landed on the boundary and is worth 20 points. The coordinates of the landing mark were of the form ( m , - m ).
Find all such coordinates. Show your steps.
Ans. i. Writes two pairs of possible coordinates such that Rohan scored 20 and 5 points for them. For examples, (1.5, 0) and (3.5, 0).
ii. Finds the distance of (2, 2.5) from (0, 0) as:
√(4 + 6.25) = √10.25 units
Hence, concludes that 5 points will be awarded.
iii. Finds the distance of (1.2, 1.6) from the origin as:
√{(1.2) 2 + (1.6) 2 } = 2 units
Assumes that the second arrow lands on the boundary mark and writes that the ratio in which the first arrow divides the origin and the second arrow's landing mark is the ratio of their radii = 2:1.
Assumes the coordinates of the second arrow's landing mark as ( x , y ) and uses section formula to write:
(2𝑥+0/3 , 2𝑦+0/3) = (1.2, 1.6)
Solves the above equation to find the values of the coordinates of the second arrow's landing mark as (1.8, 2.4).
Identifies the distance between the origin and the coordinate ( m , -m ) as 2 units and uses the distance formula to write the equation as:
m 2 + (- m ) 2 = 22
Simplifies the above equation as 2 m 2 = 4.
Solves the above equation to get y as √2 and (-√2).
Finds the coordinates as (√2, -√2) and (-√2, √2)
Q. No. 6) A drone, is an aircraft without any human pilot and is controlled by a remote-control device. Its various applications include policing, surveillance, photography, precision agriculture, forest fire monitoring, river monitoring and so on.
David used an advanced drone with high resolution camera during an expedition in a forest region which could fly upto 100 m height above the ground level. David rode on an open jeep to go deeper into the forest. The initial position of drone with respect to the open jeep on which David was riding is shown below.
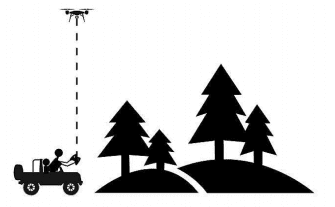
David’s jeep started moving to enter the forest at an average speed of 10 m/s. He Simultaneously started flying the drone in the same direction as that of the jeep.
(i) David reached near one of the tallest trees in the forest. He stopped the drone at a horizontal distance of 5√3 m from the top of the tree and at a vertical distance of 65 m below its maximum vertical range.
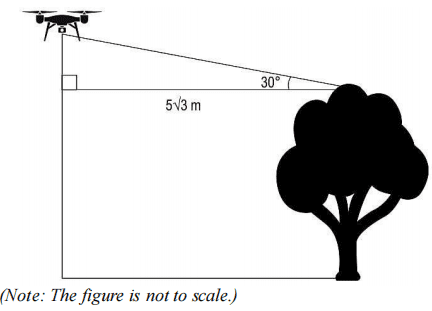
If the angle of elevation of the drone from the top of the tree was 30°, find the height of the tree. Show your work.
(ii) The drone was flying at a height of 30√3 metres at a constant speed in the horizontal direction when it spotted a zebra near a pond, right below the drone.
The drone travelled for 30 metres from there and it could see the zebra, at the same place, at an angle of depression of θ from it.
Draw a diagram to represent this situation and find θ . Show you work.
(iii) After 2 minutes of starting the expedition both the drone and the jeep stopped at the same moment so that the drone can capture some images. The position of the drone and the jeep when they stopped is as shown below.
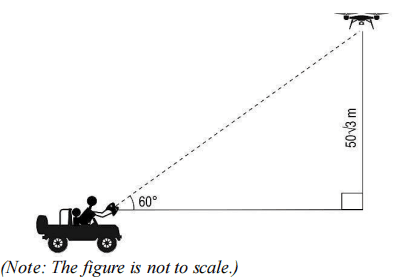
Find the average speed of the drone in m/s rounded off upto 2 decimal places. Show your work.
(iii) At some point during the expedition, David kept the drone stationary for some time to capture the images of a tiger. The angle of depression from the drone to the tiger changed from 30° to 45° in 3 seconds as shown below.
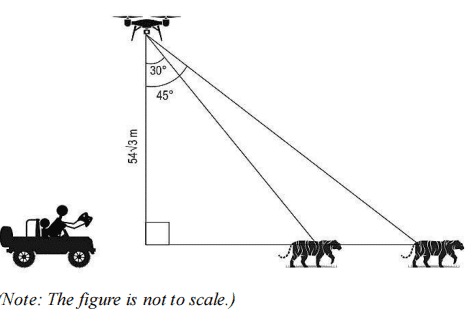
What was the average speed of the tiger during that time? Show your work.
(Note: Take √3 as 1.73.)
Ans. Assumes the vertical distance between the top of the tree and the drone to be h and finds h as:
h = 5√3 × tan 30° = 5√3 × 1/√3 = 5 m
Finds the height of the tree as 100 - 65 - 5 = 30 m
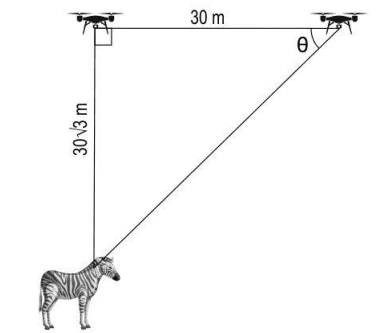
Finds the value of θ as:
tan θ = 30√3/30 = √3
Thus finds the value of θ as 60°
iii. Assumes the horizontal distance between the remote and the drone as x and finds its value as:
x = 50√3/tan60° = 50 m
Finds the distance covered by the jeep in 2 mins as:
10 × 120 = 1200 m
Finds the horizontal distance covered by the drone before it stopped as:
1200 + 50 = 1250 m
Finds the speed of the drone as:
1250/120 = 10.42 m/s
Assumes the horizontal distance between the drone and the tiger to be x when the angle of depression was 30° and finds the value of x as:
x = 54√3 × tan 30° = 54√3 × 1/√3 = 54 m
Assumes the horizontal distance between the drone and the tiger after 3 seconds as y and finds the value of y as:
y = 54√3 × tan 45° = 54√3 m
Finds the distance covered by the tiger in 3 seconds as:
54√3 - 54 = 39.42 m
Finds the average speed of the tiger during that time as:
39.42/3 = 13.14 m/s
Q. No. 7) Shown below is the trophy shield Akshi received on winning an international Table tennis tournament. The trophy is made of a glass sector DOC supported by identical wooden right triangles ∆ DAO and ∆ COB. Also, AO = 7 cm and AO : DA = 1 ∶ √3 (Use √3 = 1.73)
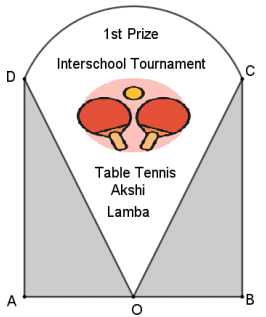
Based on the given information, answer the following questions:
(i) Find ∠𝐷𝑂𝐶
(ii) Find the area of the wooden triangles
(iii) Find the area of the shape formed by the glass portion
If Akshi wants to decorate the boundary of the glass portion with glitter tape, then find the length of the tape she needs.
Ans. (i) Let ∠𝐷𝑂𝐴 = 𝜃, then tan 𝜃 =𝐴𝐷/𝐴𝑂 = √3/1 ⟹ 𝜃 = 60° ∠𝐷𝑂𝐴 = ∠𝐶𝑂𝐵 = 60° ∠𝐷𝑂𝐶 = 180° − (60° + 60°) = 60°
(ii) Area of two wooden triangles = 2 × 1/2 × 7 × 7√3 = 84.77 𝑐𝑚 2 (iii) 𝐴𝑂/𝐷𝑂 = cos 60° ⟹ 7/𝐷𝑂 = 1/2 ⟹ 𝐷𝑂 = 14 𝑐𝑚 Area of sector 𝐷𝑂𝐶 = 60/360 × 𝜋 × 14 2 = 102.67 𝑐𝑚 2
𝐴𝑂/𝐷𝑂 = cos 60° ⟹ 7/𝐷𝑂 = 1/2 ⟹ 𝐷𝑂 = 14 𝑐𝑚 Length of tape required = 2 × 14 + 60/360 × 2 × 𝜋 × 14 = 42.67 cm
Q. No. 8) A school auditorium has to be constructed with a capacity of 2000 people. The chairs in the auditorium are arranged in a concave shape facing towards the stage in such a way that each succeeding row has 5 seats more than the previous one.

(i) If the first row has 15 seats, then how many seats will be there in 12 th row?
(ii) If there are 15 rows in the auditorium, then how many seats will be there in the middle row?
(iii) If total 1875 guests were there in the auditorium for a particular event, then how many rows will be needed to make all of them sit?
If total 1250 guests were there in the auditorium for a particular event, then how many rows will be left blank out of total 30 rows?
Ans. (i) 𝑎 = 15, 𝑑 = 5
𝑎 12 = 15 + 11×5 = 70
(ii) 𝑛 = 15
Middle row = 8th row
𝑎8 = 15 + 7 × 5 = 50
(iii) 1875 = 𝑛/2 [2 × 15 + (𝑛 − 1) × 5]
⟹ 𝑛 2 + 5𝑛 − 750 = 0
⟹ (𝑛 + 30)(𝑛 − 25) = 0 ⟹ 𝑛 = 25
∴ Total number of rows required = 25
1250 = 𝑛/2 [2×15 +(𝑛 − 1) × 5]
⟹ 𝑛 2 + 5𝑛 − 500 = 0
(𝑛 + 25)(𝑛 − 20) = 0 ⟹ 𝑛 = 20
∴ Number of rows left = 30 − 20 = 10
Q. No. 9) The students of Class X of a secondary school have been allotted a rectangular plot of land for their gardening activity. Saplings are being planted on the boundary at a distance of 1 m from each other. There is a triangular grassy lawn in the plot as shown in the figure. The students are to row seeds of the flowering plant on the remaining area of the plot.
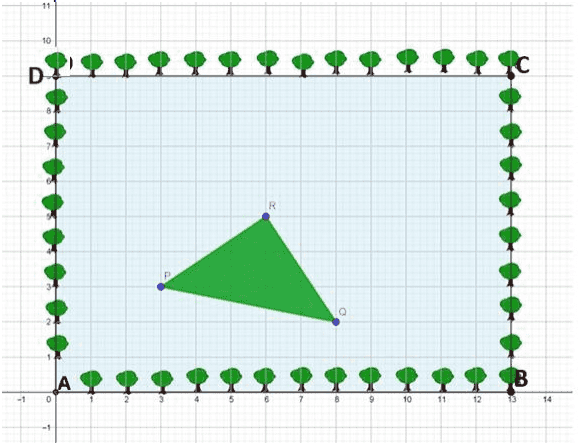
(i) If a tree is to be planted exactly in the middle of the triangle PQR ie. at the centroid of ∆PQR to give shed to the people sitting in the lawn, then find the coordinates of the point where the tree should be planted.
(ii) What type of triangle is formed by the grassy lawn?
(iii) Find the area of the plot in which the students have to row the seeds.
If a special flowering plant has to be planted at a point which divides the line joining the points C and Q in the ratio 2:3, then find the coordinates of the point where this plant will be planted
Ans. (i) 𝑃(3,3), 𝑄(8,2), 𝑅(6,5)
Coordinates of required point are ( 3+8+6/3, 3+2+5/3) = ( 17/3 , 10/3 )
(ii) 𝑃𝑅 = 𝑄𝑅 = √13
𝑃𝑄 2 = 𝑃𝑅 2 + 𝑄𝑅 2
∴ ∆ 𝑃𝑄𝑅 is an isosceles right triangle
(iii) Area of the plot to row seeds = 13 × 9 − 1/2 × √13 × √13 = 110.5 𝑚
Coordinates of required point are ( 2×8 + 3 ×13 / 2+3 , 2×2+3×9 / 2+3 ) = (11, 31/5 )
| 🎯 ✨ |
Related Posts
Science class 10 important questions, social science class 10 important questions, forest and wildlife resources class 10 important questions and answers, mastering water resources: essential questions and answers for class 10, carbon and its compounds: tackle class 10 questions with ease, the human eye and the colourful world class 10: top q&a, power sharing class 10: important questions and answers, gender, religion, and caste class 10: top questions & answers, important questions and answers on the age of industrialization class10, 1 thought on “top case-based questions: last minute prep for cbse class 10 maths exam”.
7.56 + 6(0.09) the answer you provided in question 1 subdivision 2was wrong please correct th
Leave a Comment Cancel Reply
Your email address will not be published. Required fields are marked *
Save my name, email, and website in this browser for the next time I comment.

Class 10 Maths Case Study Questions of Chapter 1 Real Numbers
- Post author: studyrate
- Post published:
- Post category: class 10th
- Post comments: 0 Comments
Case study Questions in the Class 10 Mathematics Chapter 1 are very important to solve for your exam. Class 10 Maths Chapter 1 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving Class 10 Maths Case Study Questions Chapter 1 Real Numbers
Join our Telegram Channel, there you will get various e-books for CBSE 2024 Boards exams for Class 9th, 10th, 11th, and 12th.

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.
Real Numbers Case Study Questions With Answers
Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 1 Real Numbers
Case Study/Passage-Based Questions
Case Study 1: Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions at the end of his project as listed below. (i) For what value of n, 4 n ends in 0?
| (a) 10 | (b) when n is even |
| (c) when n is odd | (d) no value of n |
Answer: (d) no value of n
(ii) If a is a positive rational number and n is a positive integer greater than 1, then for what value of n, a n is a rational number?
| (a) when n is any even integer | (b) when n is any odd integer |
| (c) for all n > 1 | (d) only when n = 0 |
Answer: (c) for all n > 1
(iii) If x and yare two odd positive integers, then which of the following is true?
| (a) x + y is even | (b) x + y is not divisible by 4 |
| (c) x + y is odd | (d) both (a) and (b) |
Answer: (d) both (a) and (b)
(iv) The statement ‘One of every three consecutive positive integers is divisible by 3’ is
| (a) always true | (b) always false |
| (c) sometimes true | (d) None of these |
Answer: (a) always true
(v) If n is any odd integer, then n2 – 1 is divisible by
| (a) 22 | (b) 55 | (c) 88 | (d) 8 |
Answer: (d) 8
Case Study 2: HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM Based on the above information answer the following questions.
(i) If two positive integers x and y are expressible in terms of primes as x =p 2 q 3 and y=p 3 q, then which of the following is true? (a) HCF = pq 2 x LCM (b) LCM = pq 2 x HCF (c) LCM = p 2 q x HCF (d) HCF = p 2 q x LCM
Answer: (b) LCM = pq2 x HCF
ii) A boy with collection of marbles realizes that if he makes a group of 5 or 6 marbles, there are always two marbles left, then which of the following is correct if the number of marbles is p? (a) p is odd (b) p is even (c) p is not prime (d) both (b) and (c)
Answer: (d) both (b) and (c)
(iii) Find the largest possible positive integer that will divide 398, 436 and 542 leaving remainder 7, 11, 15 respectively. (a) 3 (b) 1 (c) 34 (d) 17
Answer: (d) 17
(iv) Find the least positive integer that on adding 1 is exactly divisible by 126 and 600. (a) 12600 (b) 12599 (C) 12601 (d) 12500
Answer: (b) 12599
(v) If A, B and C are three rational numbers such that 85C – 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by (a) 3 (b) 6 (c) 7 (d) 9
Answer: (a) 3
Case Study 3: Real numbers are an essential concept in mathematics that encompasses both rational and irrational numbers. Rational numbers are those that can be expressed as fractions, where the numerator and denominator are integers and the denominator is not zero. Examples of rational numbers include integers, decimals, and fractions. On the other hand, irrational numbers are those that cannot be expressed as fractions and have non-terminating and non-repeating decimal expansions. Examples of irrational numbers include √2, π (pi), and e. Real numbers are represented on the number line, which extends infinitely in both positive and negative directions. The set of real numbers is closed under addition, subtraction, multiplication, and division, making it a fundamental number system used in various mathematical operations and calculations.
Which numbers can be classified as rational numbers? a) Fractions b) Integers c) Decimals d) All of the above Answer: d) All of the above
What are rational numbers? a) Numbers that can be expressed as fractions b) Numbers that have non-terminating decimal expansions c) Numbers that extend infinitely in both positive and negative directions d) Numbers that cannot be expressed as fractions Answer: a) Numbers that can be expressed as fractions
What are examples of irrational numbers? a) √2, π (pi), e b) Integers, decimals, fractions c) Numbers with terminating decimal expansions d) Numbers that can be expressed as fractions Answer: a) √2, π (pi), e
How are real numbers represented? a) On the number line b) In complex mathematical formulas c) In algebraic equations d) In geometric figures Answer: a) On the number line
What operations are closed under the set of real numbers? a) Addition, subtraction, multiplication b) Subtraction, multiplication, division c) Addition, multiplication, division d) Addition, subtraction, multiplication, division Answer: d) Addition, subtraction, multiplication, division
Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 1 Real Numbers with Answers Pdf free download has been useful to an extent. If you have any other queries about CBSE Class 10 Maths Real Numbers Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate
You Might Also Like
Assertion reason questions class 10 science chapter 7 control and coordination, mcq class 10 english footprints without feet questions with answers english chapter 5, class 10 maths case study questions chapter 3 pair of linear equations in two variables, leave a reply cancel reply.
Save my name, email, and website in this browser for the next time I comment.
Case Study Based Questions – Class 10 Maths
CBSE has recently added Case Study Based Questions or CSQ in Maths, Science and Social Science. You can visit this article to get to practice the official Sample Papers released by CBSE by clicking over here . Also do join out telegram channel to get all the updates and to participate in Quiz by clicking here.

What is Case Study Based Questions or CSQ?
Case Study Based or CSQ are typically questions in which the paragraph or passage is given and you simply have to answer them. This questions are not very tough to solve and are introduced so that you score better marks as schools and tuition are kept closed due to the COVID Pandemic. As a result, this had to be introduced. This is resulting to us, by having 34 MCQ which is really very good for scoring 100/100 in CBSE.
How to start preparing for CSQ’s?
To start preparing for CSQ you will need to learn all the chapters very thoroughly especially all the chapters of Geometry. CSQ from Maths can include a mixture of many chapters thus preparing all the concepts is must. They will surely be helpful. After completing all your syllabus you will need to practice a lot. So scroll below to find more than 15 Case study based question.
Is it Easy, Hard or Moderate?
This questions are very simple if practiced at least 20-25 questions than you can easily score lot of good marks or you can score full in Maths!! Practice all the questions below.
How much time to give to each CSQ?
You will be getting 4 Case Study Question’s each would be having 5 sub questions out of which you have to just do 4 questions. So find the shortest and most theoretical question as theoretical questions doesn’t required much solving and it will not even take 1 min to solve. Each question should not take more than 6 min, resulting to only 24 min for 16 questions which is enough. Solving as many CSQ helps in better understanding and reducing the time for each question.
Below are more than 15 examples of CSQ’s for Maths!
1st Case Study Based Question
Shankar is having a triangular open space in his plot. He divided the land into three parts by drawing boundaries PQ and RS which are parallel to BC. Other measurements are as shown in the figure.
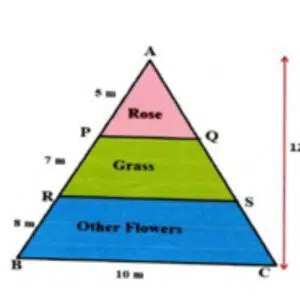
- What is the area of this land? i) 120 m 2 ii) 60 m 2 iii) 20 m 2 iv) 30 m 2
- What is the length of PQ? i) 2.5 m ii) 5 m iii) 6 m iv) 8 m
- The length of RS is i) 5 m ii) 6 m iii) 8 m iv) 4 m
- Area of △APQ is i) 7.5 m 2 ii) 10 m 2 iii) 3.75 m 2 iv) 5 m 2
- What is the area of △ARS? i) 21.6 m 2 ii) 10 m 2 iii) 3.75 m 2 iv) 6 m 2
2nd Case Study Based Question
There is some fire incident in the house. The fireman is trying to enter the house from the window as the main door is locked. The window is 6 m above the ground. He places a ladder against the wall such that its foot is at a distance of 2.5 m from the wall and its top reaches the window.

- Here, be the ladder and be the wall with the window. i) CA, AB ii) AB, AC iii) AC, BC iv) AB, BC
- We will apply Pythagoras Theorem to find length of the ladder. It is: i) AB 2 = BC 2 – CA 2 ii) CA 2 = BC 2 + AB 2 iii) BC 2 = AB 2 + CA 2 iv) AB 2 = BC 2 + CA 2
- The length of the ladder is . i) 4.5 m ii) 2.5 m iii)6.5 m iv) 5.5 m
- What would be the length of the ladder if it is placed 6 m away from the wall and the window is 8 m above the ground? i) 12 m ii) 10 m iii) 14 m iv) 8 m
- How far should the ladder be placed if the fireman gets a 9 m long ladder? i) 6.7 m (approx.) ii) 7.7 m (approx.) iii) 5.7 m (approx.) iv) 4.7 m (approx.)
3rd Case Study Based Question
In the school garden Ajay(A), Brijesh(B), Chinki(C) and Deepak(D) planted their flower plants of Rose, Sunflower, Champa and Jasmine respectively as shown in the following figure. A fifth student Eshan wanted to plant her flower in this area. The teacher instructed Eshan to plant his flower plant at a point E such that CE: EB = 3 : 2.

- Find the coordinates of point E where Eshan has to plant his flower plant. i) (5, 6) ii) (6, 5) iii) (5, 5) iv) (6, 7)
- Find the area of △ECD. i) 9.5 square unit ii) 11.5 square unit iii) 10.5 square unit iv)12.5 square unit
- Find the distance between the plants of Ajay and Deepak. i) 8.60 unit ii) 6.60 unit iii) 5.60 unit iv) 7.60 unit
- The distance between A and B is: i) 5.5 units ii) 7 units iii) 6 units iv) 5 units
- The distance between C and D is: i) 5.5 units ii) 7 units iii) 6 units iv) 5 units
4rth Case Study Based Questions
SUN ROOM The diagrams show the plans for a sun room. It will be built onto the wall of a house. The four walls of the sunroom are square clear glass panels. The roof is made using
- Four clear glass panels, trapezium in shape, all the same size.
- One tinted glass panel, half a regular octagon in shape
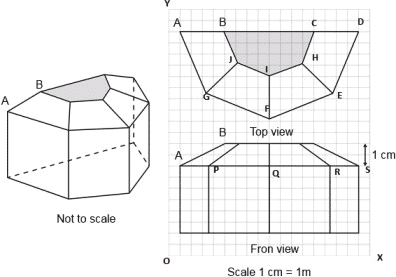
- Find the mid-point of the segment joining the points J (6, 17) and I (9, 16).[Refer to Top View] i) ( 33/2 , 15/2 ) ii) ( 3/2 , 1/2 ) iii) ( 15/2 , 33/2 ) iv) ( 1/2 , 3/2 )
- The distance of the point P from the y-axis is; [Refer to Top View] i) 4 ii) 15 iii) 19 iv) 25
- The distance between the points A and S is: [Refer to Front View] i) 4 ii) 8 iii) 16 iv) 20
- Find the coordinates of the point which divides the line segment joining the points A and B in the ratio 1:3 internally. [Refer to Front View] i) (8.5, 2.0) ii) (2.0, 9.5) iii) (3.0, 7.5) iv) (2.0, 8.5)
- If a point (x,y) is equidistant from the Q(9,8) and S(17,8), then [Refer to Front View] i) x + y = 13 ii) x – 13 = 0 iii) y – 13 = 0 iv) x – y = 13
5th Case Study based Question
Education with vocational training is helpful in making a student self-reliant and to help and serve the society. Keeping this in view, a teacher made the following table giving the frequency distribution of a student undergoing vocational training from the training institute.

- Median class of above data: i) 20 – 24 ii) 20.5 – 24.5 iii) 19.5 – 24.5 iv) 24.5 – 29.5
- Calculate the median. i) 24.06 ii) 30.07 iii) 24.77 iv) 42.07
- The empirical relationship between mean, median, mode: i) Mode = 3 Median + 2 Mean ii) Mode = 3 Median – 2 Mean iii) Mode = 3 Mean + 2 Median iv) 3 Mode = Median – 2 Mean
- If mode = 80 and mean = 110, then find the median. i) 200 ii) 500 iii) 190 iv) 100
- The mode is the: i) middlemost frequent value ii) least frequent value iii) maximum frequent value iv) none of these
6th Case Study Based Question
Two brothers Ramesh and Pulkit were at home and have to reach School. Ramesh went to Library first to return a book and then reaches School directly whereas Pulkit went to Skate Park first to meet his friend and then reaches School directly.
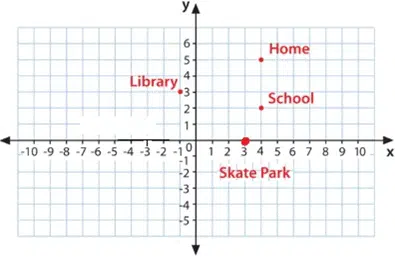
- How far is School from their Home? i) 5 m ii) 3 m iii) 2 m iv) 4 m
- What is the extra distance travelled by Ramesh in reaching his School? i) 4.48 metres ii) 6.48 metres iii) 7.48 metres iv) 8.48 metres
- What is the extra distance travelled by Pulkit in reaching his School? (All distances are measured in metres as straight lines) i) 6.33 metres ii) 7.33 metres iii) 5.33 metres iv) 4.33 metres
- The location of the library is: i) (-1, 3) ii) (1, 3) iii) (3, 1) iv) (3, -1)
- The location of the Home is: i) (4, 2) ii) (1, 3) iii) (4, 5) iv) (5,4)
7th Case Study Based Question
The Class X students of a secondary school in Krishinagar have been allotted a rectangular plot of land for their gardening activity. Sapling of Gulmohar is planted on the boundary of the plot at a distance of 1m from each other. There is a triangular grassy lawn inside the plot as shown in Fig. The students have to sow seeds of flowering plants on the remaining area of the plot.
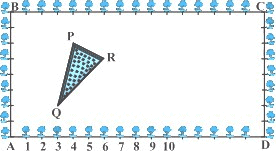
- Considering A as the origin, what are the coordinates of A? i) (0, 1) ii) (1, 0) iii) (0, 0) iv (-1, -1)
- What are the coordinates of P? i) (4, 6) ii) ( 6, 4) iii) (4, 5) iv) (5, 4)
- What are the coordinates of R? i) (6, 5) ii) (5, 6) iii) ( 6, 0) iv) (7, 4)
- What are the coordinates of D? i) (16, 0) ii) (0, 0) iii) (0, 16) iv) (16, 1)
- What are the coordinates of P if D is taken as the origin? i) (12, 2) ii) (-12, 6) iii) (12, 3) iv) (6, 10)
8th Case Study Based Question
There exist a tower near the house of Shankar. The top of the tower AB is tied with steel wire and on the ground, it is tied with string support. One day Shankar tried to measure the longest of the wire AC using Pythagoras theorem.
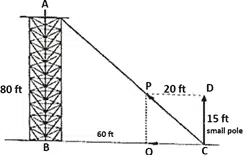
- In the figure, the length of wire AC is: (take BC = 60 ft) i) 75 ft ii) 100 ft iii) 120 ft iv) 90 ft
- What is the area of △ABC? i) 2400 ft 2 ii) 4800 ft 2 iii) 6000 ft 2 iv) 3000 ft 2
- What is the length of the wire PC? i) 20 ft ii) 30 ft iii) 25 ft iv) 40 ft
- What is the length of the hypotenuse in △ABC? i) 100 ft ii) 80 ft iii) 60 ft iv) 120 ft
- What is the area of a △POC? 100 ft 2 150 ft 2 200 ft 2 250 ft 2
9th Case Study Based Question
- SCALE FACTOR AND SIMILARITY SCALE FACTOR: A scale drawing of an object is the same shape as the object but a different size. The scale of a drawing is a comparison of the length used on a drawing to the length it represents. The scale is written as a ratio. SIMILAR FIGURES: The ratio of two corresponding sides in similar figures is called the scale factor. Hence, two shapes are Similar when one can become the other after a resize, flip, slide, or turn.
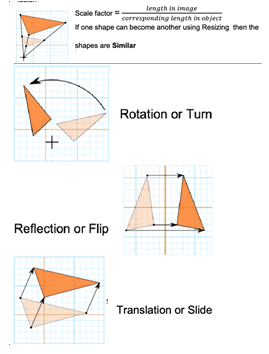
- A model of a boat is made on a scale of 1:4. The model is 120cm long. The full size of the boat has a width of 60cm. What is the width of the scale model? i) 20 cm ii) 25 cm iii) 15 cm iv) 240 cm
- What will affect the similarity of any two polygons? i) They are flipped horizontally ii) They are dilated by a scale factor iii) They are translated down iv) They are not the mirror image of one another
- If two similar triangles have a scale factor of a: b. Which statement regarding the two triangles is true? i) The ratio of their perimeters is 3a: b ii) Their altitudes have a ratio a: b iii) Their medians have a ratio a/2:b iv)Their angle bisector have a ration a 2 :b 2
- The shadow of a stick 5m long is 2m. At the same time, the shadow of a tree 12.5m high is: i) 3m ii)3.5m iii)4.5m iv)5m
- Below you see a student’s mathematical model of a farmhouse roof with measurements. The attic floor, ABCD in the model, is a square. The beams that support the roof are the edges of a rectangular prism, EFGHKLMN. E is the middle of AT, F is the middle of BT, G is the middle of CT, and H is the middle of DT. All the edges of the pyramid in the model have a length of 12 m.
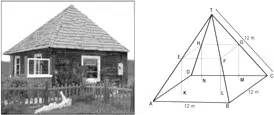
What is the length of EF, where EF is one of the horizontal edges of the block? i) 24m ii) 3m iii) 6m iv) 10m
10th Case Study Based Question
An Aeroplan leaves an Airport and flies due north at 300 km/h. At the same time, another Aeroplan leaves the same Airport and flies due west at 400 km/h.
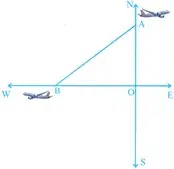
- Distance travelled by the first Airplane in 1.5 hours i) 450 km ii) 300 km iii) 150 km iv) 600 km
- Distance travelled by the second Airplane in 1.5 hours i) 450 km ii) 300 km iii) 150 km iv) 600 km
- Which of the following line segment shows the distance between both the airplane? i) OA ii) AB iii) OB iv) WB
- Which airplane travelled a long distance and by how many km? i) Second, 150 km ii) Second, 250 km iii) First, 150 km iv) First, 250 km
- How far apart the two airplanes would be after 1.5 hours? i) 600 km ii) 750 km iii) 300 km iv) 150 km
Leave a Comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.

Gurukul of Excellence
Classes for Physics, Chemistry and Mathematics by IITians
Join our Telegram Channel for Free PDF Download
Case Study Questions for Class 10 Maths Chapter 1 Real Numbers
- Last modified on: 12 months ago
- Reading Time: 7 Minutes
Question 1:
HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM Based on the above information answer the following questions.
(i) If two positive integers x and y are expressible in terms of primes as x =p 2 q 3 and y=p 3 q, then which of the following is true? (a) HCF = pq 2 x LCM (b) LCM = pq 2 x HCF (c) LCM = p 2 q x HCF (d) HCF = p 2 q x LCM
(ii) A boy with collection of marbles realizes that if he makes a group of 5 or 6 marbles, there are always two marbles left, then which of the following is correct if the number of marbles is p? (a) p is odd (b) p is even (c) p is not prime (d) both (b) and (c)
(iii) Find the largest possible positive integer that will divide 398, 436 and 542 leaving remainder 7, 11, 15 respectively. (a) 3 (b) 1 (c) 34 (d) 17
(iv) Find the least positive integer which on adding 1 is exactly divisible by 126 and 600. (a) 12600 (b) 12599 (C) 12601 (d) 12500
(v) If A, B and C are three rational numbers such that 85C – 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by (a) 3 (b) 6 (c) 7 (d) 9
Question 2:
To enhance the reading skills of grade X students, the school nominates you and two of your friends to set up a class library. There are two sections- section A and section B of grade X. There are 32 students in section A and 36 students in section B.
(i) What is the minimum number of books you will acquire for the class library, so that they can be distributed equally among students of Section A or Section B? (a) 144 (b) 128 (c) 288 (d) 272
(ii) If the product of two positive integers is equal to the product of their HCF and LCM is true then, the HCF (32 , 36) is (a) 2 (b) 4 (c) 6 (d) 8
(iii) 36 can be expressed as a product of its primes as (a) (b) (c) (d)
(iv) 7 is a (a) Prime number (b) Composite number (c) Neither prime nor composite (d) None of the above
(v) If p and q are positive integers such that p = a and q= b, where a , b are prime numbers, then the LCM (p, q) is (a) ab (b) a 2 b 2 (c) a 3 b 2 (d) a 3 b 3
✨ Free Quizzes, Test Series and Learning Videos for CBSE Class 10 Maths
You may also like:
Chapter 1 Real Numbers Chapter 2 Polynomials Chapter 3 Pair of Linear Equations in Two Variables C hapter 4 Quadratic Equations Chapter 5 Arithmetic Progressions Chapter 6 Triangles Chapter 7 Coordinate Geometry Chapter 8 Introduction to Trigonometry Chapter 9 Some Applications of Trigonometry Chapter 10 Circles Chapter 11 Constructions Chapter 12 Areas Related to Circles Chapter 13 Surface Areas and Volumes Chapter 14 Statistics Chapter 15 Probability
Download CBSE Books
Exam Special Series:
- Sample Question Paper for CBSE Class 10 Science (for 2024)
- Sample Question Paper for CBSE Class 10 Maths (for 2024)
- CBSE Most Repeated Questions for Class 10 Science Board Exams
- CBSE Important Diagram Based Questions Class 10 Physics Board Exams
- CBSE Important Numericals Class 10 Physics Board Exams
- CBSE Practical Based Questions for Class 10 Science Board Exams
- CBSE Important “Differentiate Between” Based Questions Class 10 Social Science
- Sample Question Papers for CBSE Class 12 Physics (for 2024)
- Sample Question Papers for CBSE Class 12 Chemistry (for 2024)
- Sample Question Papers for CBSE Class 12 Maths (for 2024)
- Sample Question Papers for CBSE Class 12 Biology (for 2024)
- CBSE Important Diagrams & Graphs Asked in Board Exams Class 12 Physics
- Master Organic Conversions CBSE Class 12 Chemistry Board Exams
- CBSE Important Numericals Class 12 Physics Board Exams
- CBSE Important Definitions Class 12 Physics Board Exams
- CBSE Important Laws & Principles Class 12 Physics Board Exams
- 10 Years CBSE Class 12 Chemistry Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Physics Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Maths Previous Year-Wise Solved Papers (2023-2024)
- 10 Years CBSE Class 12 Biology Previous Year-Wise Solved Papers (2023-2024)
- ICSE Important Numericals Class 10 Physics BOARD Exams (215 Numericals)
- ICSE Important Figure Based Questions Class 10 Physics BOARD Exams (230 Questions)
- ICSE Mole Concept and Stoichiometry Numericals Class 10 Chemistry (65 Numericals)
- ICSE Reasoning Based Questions Class 10 Chemistry BOARD Exams (150 Qs)
- ICSE Important Functions and Locations Based Questions Class 10 Biology
- ICSE Reasoning Based Questions Class 10 Biology BOARD Exams (100 Qs)
✨ Join our Online JEE Test Series for 499/- Only (Web + App) for 1 Year
✨ Join our Online NEET Test Series for 499/- Only for 1 Year
Leave a Reply Cancel reply
Join our Online Test Series for CBSE, ICSE, JEE, NEET and Other Exams

Editable Study Materials for Your Institute - CBSE, ICSE, State Boards (Maharashtra & Karnataka), JEE, NEET, FOUNDATION, OLYMPIADS, PPTs
Discover more from Gurukul of Excellence
Subscribe now to keep reading and get access to the full archive.
Type your email…
Continue reading

- Andhra Pradesh
- Chhattisgarh
- West Bengal
- Madhya Pradesh
- Maharashtra
- Jammu & Kashmir
- NCERT Books 2022-23
- NCERT Solutions
- NCERT Notes
- NCERT Exemplar Books
- NCERT Exemplar Solution
- States UT Book
- School Kits & Lab Manual
- NCERT Books 2021-22
- NCERT Books 2020-21
- NCERT Book 2019-2020
- NCERT Book 2015-2016
- RD Sharma Solution
- TS Grewal Solution
- TR Jain Solution
- Selina Solution
- Frank Solution
- Lakhmir Singh and Manjit Kaur Solution
- I.E.Irodov solutions
- ICSE - Goyal Brothers Park
- ICSE - Dorothy M. Noronhe
- Sandeep Garg Textbook Solution
- Micheal Vaz Solution
- S.S. Krotov Solution
- Evergreen Science
- KC Sinha Solution
- ICSE - ISC Jayanti Sengupta, Oxford
- ICSE Focus on History
- ICSE GeoGraphy Voyage
- ICSE Hindi Solution
- ICSE Treasure Trove Solution
- Thomas & Finney Solution
- SL Loney Solution
- SB Mathur Solution
- P Bahadur Solution
- Narendra Awasthi Solution
- MS Chauhan Solution
- LA Sena Solution
- Integral Calculus Amit Agarwal Solution
- IA Maron Solution
- Hall & Knight Solution
- Errorless Solution
- Pradeep's KL Gogia Solution
- OP Tandon Solutions
- Sample Papers
- Previous Year Question Paper
- Important Question
- Value Based Questions
- CBSE Syllabus
- CBSE MCQs PDF
- Assertion & Reason
- New Revision Notes
- Revision Notes
- Question Bank
- Marks Wise Question
- Toppers Answer Sheets
- Exam Paper Aalysis
- Concept Map
- CBSE Text Book
- Additional Practice Questions
- Vocational Book
- CBSE - Concept
- KVS NCERT CBSE Worksheets
- Formula Class Wise
- Formula Chapter Wise
- JEE Previous Year Paper
- JEE Mock Test
- JEE Crash Course
- JEE Sample Papers
- Important Info
- SRM-JEEE Previous Year Paper
- SRM-JEEE Mock Test
- VITEEE Previous Year Paper
- VITEEE Mock Test
- BITSAT Previous Year Paper
- BITSAT Mock Test
- Manipal Previous Year Paper
- Manipal Engineering Mock Test
- AP EAMCET Previous Year Paper
- AP EAMCET Mock Test
- COMEDK Previous Year Paper
- COMEDK Mock Test
- GUJCET Previous Year Paper
- GUJCET Mock Test
- KCET Previous Year Paper
- KCET Mock Test
- KEAM Previous Year Paper
- KEAM Mock Test
- MHT CET Previous Year Paper
- MHT CET Mock Test
- TS EAMCET Previous Year Paper
- TS EAMCET Mock Test
- WBJEE Previous Year Paper
- WBJEE Mock Test
- AMU Previous Year Paper
- AMU Mock Test
- CUSAT Previous Year Paper
- CUSAT Mock Test
- AEEE Previous Year Paper
- AEEE Mock Test
- UPSEE Previous Year Paper
- UPSEE Mock Test
- CGPET Previous Year Paper
- Crash Course
- Previous Year Paper
- NCERT Based Short Notes
- NCERT Based Tests
- NEET Sample Paper
- Previous Year Papers
- Quantitative Aptitude
- Numerical Aptitude Data Interpretation
- General Knowledge
- Mathematics
- Agriculture
- Accountancy
- Business Studies
- Political science
- Enviromental Studies
- Mass Media Communication
- Teaching Aptitude
- Verbal Ability & Reading Comprehension
- Logical Reasoning & Data Interpretation
- NAVODAYA VIDYALAYA
- SAINIK SCHOOL (AISSEE)
- Mechanical Engineering
- Electrical Engineering
- Electronics & Communication Engineering
- Civil Engineering
- Computer Science Engineering
- CBSE Board News
- Scholarship Olympiad
- School Admissions
- Entrance Exams
- All Board Updates
- Miscellaneous
- State Wise Books
- Engineering Exam
Case Study on Probability Class 10 Maths PDF
The passage-based questions are commonly known as case study questions. Students looking for Case Study on Probability Class 10 Maths can use this page to download the PDF file.
The case study questions on Probability are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Probability case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 Maths board examination. Continue reading to know how should students answer it and why it is essential to solve it, etc.
Case Study on Probability Class 10 Maths with Solutions in PDF
Our experts have also kept in mind the challenges students may face while solving the case study on Probability, therefore, they prepared a set of solutions along with the case study questions on Probability.
The case study on Probability Class 10 Maths with solutions in PDF helps students tackle questions that appear confusing or difficult to answer. The answers to the Probability case study questions are very easy to grasp from the PDF - download links are given on this page.
Why Solve Probability Case Study Questions on Class 10 Maths?
There are three major reasons why one should solve Probability case study questions on Class 10 Maths - all those major reasons are discussed below:
- To Prepare for the Board Examination: For many years CBSE board is asking case-based questions to the Class 10 Maths students, therefore, it is important to solve Probability Case study questions as it will help better prepare for the Class 10 board exam preparation.
- Develop Problem-Solving Skills: Class 10 Maths Probability case study questions require students to analyze a given situation, identify the key issues, and apply relevant concepts to find out a solution. This can help CBSE Class 10 students develop their problem-solving skills, which are essential for success in any profession rather than Class 10 board exam preparation.
- Understand Real-Life Applications: Several Probability Class 10 Maths Case Study questions are linked with real-life applications, therefore, solving them enables students to gain the theoretical knowledge of Probability as well as real-life implications of those learnings too.
How to Answer Case Study Questions on Probability?
Students can choose their own way to answer Case Study on Probability Class 10 Maths, however, we believe following these three steps would help a lot in answering Class 10 Maths Probability Case Study questions.
- Read Question Properly: Many make mistakes in the first step which is not reading the questions properly, therefore, it is important to read the question properly and answer questions accordingly.
- Highlight Important Points Discussed in the Clause: While reading the paragraph, highlight the important points discussed as it will help you save your time and answer Probability questions quickly.
- Go Through Each Question One-By-One: Ideally, going through each question gradually is advised so, that a sync between each question and the answer can be maintained. When you are solving Probability Class 10 Maths case study questions make sure you are approaching each question in a step-wise manner.
What to Know to Solve Case Study Questions on Class 10 Probability?
A few essential things to know to solve Case Study Questions on Class 10 Probability are -
- Basic Formulas of Probability: One of the most important things to know to solve Case Study Questions on Class 10 Probability is to learn about the basic formulas or revise them before solving the case-based questions on Probability.
- To Think Analytically: Analytical thinkers have the ability to detect patterns and that is why it is an essential skill to learn to solve the CBSE Class 10 Maths Probability case study questions.
- Strong Command of Calculations: Another important thing to do is to build a strong command of calculations especially, mental Maths calculations.
Where to Find Case Study on Probability Class 10 Maths?
Use Selfstudys.com to find Case Study on Probability Class 10 Maths. For ease, here is a step-wise procedure to download the Probability Case Study for Class 10 Maths in PDF for free of cost.
Since you are already on this page, you can scroll to the top section of this page to get access to the Case Study on Probability. To help others reach this page let them know these steps:
- Open Selfstudys.com on your computer/laptop or Smartphone
- Once the website gets loaded, click on the navigation button
- Find CBSE from the given menu
- Click on Case Study
- Choose Class 10
- Search Maths and then navigate to the Probability Class 10 Maths Case Study
- NCERT Solutions for Class 12 Maths
- NCERT Solutions for Class 10 Maths
- CBSE Syllabus 2023-24
- Social Media Channels
- Login Customize Your Notification Preferences

One Last Step...

- Second click on the toggle icon

Provide prime members with unlimited access to all study materials in PDF format.
Allow prime members to attempt MCQ tests multiple times to enhance their learning and understanding.
Provide prime users with access to exclusive PDF study materials that are not available to regular users.

CBSE Expert
Class 10 Maths: Case Study Questions of Chapter 10 Circles PDF
Case study Questions on the Class 10 Mathematics Chapter 10 are very important to solve for your exam. Class 10 Maths Chapter 10 Case Study Questions have been prepared for the latest exam pattern. You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 10 Circles

In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason . There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ questions based on it will be asked.
Circles Case Study Questions With answers
Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 10 Circles
Case Study/Passage Based Questions
Smita always finds it confusing with the concepts of tangent and secant of a circle. But this time she has determined herself to get concepts easier. So, she started listing down the differences between tangent and secant of a circle along with their relation. Here, some points in question form are listed by Smita in her notes.
A line that intersects a circle exactly at two points is called (a) Secant (b) Tangent (c) Chord (d) Both (a) and (b)
Answer: (a) Secant
The number of tangents that can be drawn on a circle is (a) 1 (b) 0 (c) 2 (d) Infinite
Answer: (d) Infinite
The number of tangents that can be drawn to a circle from a point, not on it, is (a) 1 (b) 2 (c) 0 (d) Infinite
Answer: (b) 2
Number of secants that can be drawn to a circle from a point on it is (a) infinite (b) 1 (c) 2 (d) 0
Answer: (a) infinite
A line that touches a circle at only one point is called (a) Secant (b) Chord (c) Tangent (d) Diameter
Answer: (c) Tangent
If a tangent is drawn to a circle from an external point, then the radius at the point of contact is perpendicular to the tangent.
Two concentric circles are of radii 5 cm and 3 cm. Find the length of the chord of the larger circle which touches the smaller circle. (a) 8 cm (b) 4 cm (c) 10 cm (d) 6 cm
Answer: (a) 8 cm
In the given figure, O is the centre of two concentric circles of radii 5 cm and 3 cm. From an external point P tangent, PA and PB are drawn to these circles. If PA = 12 cm, then PB =
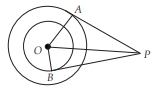
(a) 2√10 cm (b) 2√5 cm (c) 4√10 cm (d) 4√5 cm
Answer: (c) 4√10 cm
The diameter of the two concentric circles is 10 cm and 6 cm. AB is the diameter of the bigger circle and BD is the tangent to the smaller circle touching it at D and intersecting the larger circle at P on producing. Find the length of BP.
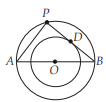
Answer: (d) 8 cm
Two concentric circles are such that the difference between their radii is 4 cm and the length of the chord of the larger circle which touches the smaller circle is 24 cm. Then the radius of the smaller circle is (a) 16 cm (b) 20 cm (c) 18 cm (d) None of these
Answer: (a) 16 cm
Hope the information shed above regarding Case Study and Passage Based Questions for Class 10 Maths Chapter 10 Circles with Answers Pdf free download has been useful to an extent. If you have any other queries of CBSE Class 10 Maths Circles Case Study and Passage Based Questions with Answers, feel free to comment below so that we can revert back to us at the earliest possible By Team Study Rate
Leave a Comment Cancel reply
Save my name, email, and website in this browser for the next time I comment.
Download India's best Exam Preparation App Now.
Key Features
- Revision Notes
- Important Questions
- Previous Years Questions
- Case-Based Questions
- Assertion and Reason Questions
No thanks, I’m not interested!
Information
- Author Services
Initiatives
You are accessing a machine-readable page. In order to be human-readable, please install an RSS reader.
All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess .
Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications.
Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers.
Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal.
Original Submission Date Received: .
- Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia

Article Menu

- Subscribe SciFeed
- Recommended Articles
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website.
Please let us know what you think of our products and services.
Visit our dedicated information section to learn more about MDPI.
JSmol Viewer
Estimating cross-border mobility from the difference in peak timing: a case study of poland–germany border regions.

1. Introduction
2.1. deterministic model, 2.2. stochastic model, case study: covid-19 incidence in poland–germany border region, 4. discussion, author contributions, data availability statement, conflicts of interest.
- Brockmann, D. Human mobility and spatial disease dynamics. Rev. Nonlinear Dyn. Complex. 2009 , 2 , 1–24. [ Google Scholar ]
- Findlater, A.; Bogoch, I.I. Human mobility and the global spread of infectious diseases: A focus on air travel. Trends Parasitol. 2018 , 34 , 772–783. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Alessandretti, L.; Aslak, U.; Lehmann, S. The scales of human mobility. Nature 2020 , 587 , 402–407. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Barbosa, H.; Barthelemy, M.; Ghoshal, G.; James, C.R.; Lenormand, M.; Louail, T.; Menezes, R.; Ramasco, J.J.; Simini, F.; Tomasini, M. Human mobility: Models and applications. Phys. Rep. 2018 , 734 , 1–74. [ Google Scholar ] [ CrossRef ]
- Schläpfer, M.; Dong, L.; O’Keeffe, K.; Santi, P.; Szell, M.; Salat, H.; Anklesaria, S.; Vazifeh, M.; Ratti, C.; West, G.B. The universal visitation law of human mobility. Nature 2021 , 593 , 522–527. [ Google Scholar ] [ CrossRef ]
- Wilder-Smith, A.; Gubler, D.J. Geographic expansion of dengue: The impact of international travel. Med. Clin. N. Am. 2008 , 92 , 1377–1390. [ Google Scholar ] [ CrossRef ]
- Cavallaro, F.; Dianin, A. Cross-border commuting in Central Europe: Features, trends and policies. Transp. Policy 2019 , 78 , 86–104. [ Google Scholar ] [ CrossRef ]
- Docquier, F.; Golenvaux, N.; Nijssen, S.; Schaus, P.; Stips, F. Cross-border mobility responses to COVID-19 in Europe: New evidence from facebook data. Glob. Health 2022 , 18 , 41. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Shyamsunder; Bhatter, S.; Jangid, K.; Abidemi, A.; Owolabi, K.M.; Purohit, S.D. A new fractional mathematical model to study the impact of vaccination on COVID-19 outbreaks. Decis. Anal. J. 2023 , 6 , 100156. [ Google Scholar ]
- Kumawat, S.; Bhatter, S.; Suthar, D.; Purohit, S.; Jangid, K. Numerical modeling on age-based study of coronavirus transmission. Appl. Math. Sci. Eng. 2022 , 30 , 609–634. [ Google Scholar ] [ CrossRef ]
- Shubin, M.; Brustad, H.K.; Midtbo, J.E.; Gunther, F.; Alessandretti, L.; Ala-Nissila, T.; Scalia Tomba, G.; Kivela, M.; Yat Hin Chan, L.; Leskela, L. The influence of cross-border mobility on the COVID-19 epidemic in Nordic countries. medRxiv 2023 , 2023–11. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Kühn, M.J.; Abele, D.; Binder, S.; Rack, K.; Klitz, M.; Kleinert, J.; Gilg, J.; Spataro, L.; Koslow, W.; Siggel, M.; et al. Regional opening strategies with commuter testing and containment of new SARS-CoV-2 variants in Germany. BMC Infect. Dis. 2022 , 22 , 333. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Balcan, D.; Colizza, V.; Gonçalves, B.; Hu, H.; Ramasco, J.J.; Vespignani, A. Multiscale mobility networks and the spatial spreading of infectious diseases. Proc. Natl. Acad. Sci. USA 2009 , 106 , 21484–21489. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Jandarov, R.; Haran, M.; Bjørnstad, O.; Grenfell, B. Emulating a gravity model to infer the spatiotemporal dynamics of an infectious disease. J. R. Stat. Soc. Ser. (Appl. Stat.) 2014 , 63 , 423–444. [ Google Scholar ] [ CrossRef ]
- Xia, Y.; Bjørnstad, O.N.; Grenfell, B.T. Measles metapopulation dynamics: A gravity model for epidemiological coupling and dynamics. Am. Nat. 2004 , 164 , 267–281. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Senapati, A.; Sardar, T.; Ganguly, K.S.; Ganguly, K.S.; Chattopadhyay, A.K.; Chattopadhyay, J. Impact of adult mosquito control on dengue prevalence in a multi-patch setting: A case study in Kolkata (2014–2015). J. Theor. Biol. 2019 , 478 , 139–152. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Mari, L.; Bertuzzo, E.; Righetto, L.; Casagrandi, R.; Gatto, M.; Rodriguez-Iturbe, I.; Rinaldo, A. Modelling cholera epidemics: The role of waterways, human mobility and sanitation. J. R. Soc. Interface 2012 , 9 , 376–388. [ Google Scholar ] [ CrossRef ]
- Yang, W.; Zhang, W.; Kargbo, D.; Yang, R.; Chen, Y.; Chen, Z.; Kamara, A.; Kargbo, B.; Kandula, S.; Karspeck, A.; et al. Transmission network of the 2014–2015 Ebola epidemic in Sierra Leone. J. R. Soc. Interface 2015 , 12 , 20150536. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Mertel, A.; Vyskočil, J.; Schüler, L.; Schlechte-Wełnicz, W.; Calabrese, J.M. Fine-scale variation in the effect of national border on COVID-19 spread: A case study of the Saxon-Czech border region. Spat. Spatio-Temporal Epidemiol. 2023 , 44 , 100560. [ Google Scholar ] [ CrossRef ]
- Simini, F.; González, M.C.; Maritan, A.; Barabási, A.L. A universal model for mobility and migration patterns. Nature 2012 , 484 , 96–100. [ Google Scholar ] [ CrossRef ]
- Timme, M. Revealing network connectivity from response dynamics. Phys. Rev. Lett. 2007 , 98 , 224101. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Casadiego, J.; Nitzan, M.; Hallerberg, S.; Timme, M. Model-free inference of direct network interactions from nonlinear collective dynamics. Nat. Commun. 2017 , 8 , 2192. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Shandilya, S.G.; Timme, M. Inferring network topology from complex dynamics. New J. Phys. 2011 , 13 , 013004. [ Google Scholar ] [ CrossRef ]
- Gao, T.T.; Yan, G. Autonomous inference of complex network dynamics from incomplete and noisy data. Nat. Comput. Sci. 2022 , 2 , 160–168. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Ching, E.S.; Lai, P.Y.; Leung, C. Reconstructing weighted networks from dynamics. Phys. Rev. 2015 , 91 , 030801. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Shi, L.; Shen, C.; Jin, L.; Shi, Q.; Wang, Z.; Boccaletti, S. Inferring network structures via signal Lasso. Phys. Rev. Res. 2021 , 3 , 043210. [ Google Scholar ] [ CrossRef ]
- Alves, C.L.; Pineda, A.M.; Roster, K.; Thielemann, C.; Rodrigues, F.A. EEG functional connectivity and deep learning for automatic diagnosis of brain disorders: Alzheimer’s disease and schizophrenia. J. Phys. Complex. 2022 , 3 , 025001. [ Google Scholar ] [ CrossRef ]
- Sysoeva, M.V.; Sysoev, I.V.; Prokhorov, M.D.; Ponomarenko, V.I.; Bezruchko, B.P. Reconstruction of coupling structure in network of neuron-like oscillators based on a phase-locked loop. Chaos Solitons Fractals 2021 , 142 , 110513. [ Google Scholar ] [ CrossRef ]
- Hempel, K.; Earn, D.J. Estimating epidemic coupling between populations from the time to invasion. J. R. Soc. Interface 2020 , 17 , 20200523. [ Google Scholar ] [ CrossRef ]
- Bichara, D.; Kang, Y.; Castillo-Chavez, C.; Horan, R.; Perrings, C. SIS and SIR epidemic models under virtual dispersal. Bull. Math. Biol. 2015 , 77 , 2004–2034. [ Google Scholar ] [ CrossRef ]
- Bichara, D.; Iggidr, A. Multi-patch and multi-group epidemic models: A new framework. J. Math. Biol. 2018 , 77 , 107–134. [ Google Scholar ] [ CrossRef ]
- Espinoza, B.; Castillo-Chavez, C.; Perrings, C. Mobility restrictions for the control of epidemics: When do they work? PLoS ONE 2020 , 15 , e0235731. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Mhlanga, A.; Mupedza, T. A patchy theoretical model for the transmission dynamics of SARS-cov-2 with optimal control. Sci. Rep. 2022 , 12 , 17840. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Agusto, F.; Goldberg, A.; Ortega, O.; Ponce, J.; Zaytseva, S.; Sindi, S.; Blower, S. How do interventions impact malaria dynamics between neighboring countries? A case study with Botswana and Zimbabwe. In Using Mathematics to Understand Biological Complexity: From Cells to Populations ; Association for Women in Mathematics Series; Springer: Cham, Switerland, 2021; Volume 22, pp. 83–109. [ Google Scholar ] [ CrossRef ]
- Gillespie, D.T. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 2001 , 115 , 1716–1733. [ Google Scholar ] [ CrossRef ]
- Gillespie, D.T.; Petzold, L.R. Improved leap-size selection for accelerated stochastic simulation. J. Chem. Phys. 2003 , 119 , 8229–8234. [ Google Scholar ] [ CrossRef ]
- Linka, K.; Peirlinck, M.; Kuhl, E. The reproduction number of COVID-19 and its correlation with public health interventions. Comput. Mech. 2020 , 66 , 1035–1050. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Abdussalam, W.; Mertel, A.; Fan, K.; Schüler, L.; Schlechte-Wełnicz, W.; Calabrese, J.M. A scalable pipeline for COVID-19: The case study of Germany, Czechia and Poland. arXiv 2022 , arXiv:2208.12928. [ Google Scholar ]
- Byrne, A.W.; McEvoy, D.; Collins, A.B.; Hunt, K.; Casey, M.; Barber, A.; Butler, F.; Griffin, J.; Lane, E.A.; McAloon, C.; et al. Inferred duration of infectious period of SARS-CoV-2: Rapid scoping review and analysis of available evidence for asymptomatic and symptomatic COVID-19 cases. BMJ Open 2020 , 10 , e039856. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Ma, J. Estimating epidemic exponential growth rate and basic reproduction number. Infect. Dis. Model. 2020 , 5 , 129–141. [ Google Scholar ] [ CrossRef ]
- Favier, C.; Dégallier, N.; Rosa-Freitas, M.G.; Boulanger, J.P.; Costa Lima, J.; Luitgards-Moura, J.F.; Menkes, C.E.; Mondet, B.; Oliveira, C.; Weimann, E.; et al. Early determination of the reproductive number for vector-borne diseases: The case of dengue in Brazil. Trop. Med. Int. Health 2006 , 11 , 332–340. [ Google Scholar ] [ CrossRef ]
- Pinho, S.T.R.d.; Ferreira, C.P.; Esteva, L.; Barreto, F.R.; Morato e Silva, V.; Teixeira, M. Modelling the dynamics of dengue real epidemics. Philos. Trans. R. Soc. Math. Phys. Eng. Sci. 2010 , 368 , 5679–5693. [ Google Scholar ] [ CrossRef ] [ PubMed ]
Click here to enlarge figure
| Pair (Powiat, Kreise) | Transmission Rate ( , ) | Total Population ( , ) | Initial Infection | Observed Difference in Peak Timing ( ) | Estimated Mobility Flux ( ) |
|---|---|---|---|---|---|
| (Gryfiński, Uckermark) | (0.10, 0.075) | (82,951, 119,552) | (11, 8) | 20 days | 0.038 [0.022, 0.064] |
| (Słubicki, Frankfurt(Oder)) | (0.13, 0.14) | (47,068, 57,873) | (8, 1) | 10 days | 0.032 [0.004, 0.052] |
| (Zgorzelecki, Görlitz) | (0.10, 0.11) | (90,584, 254,894) | (9, 23) | 20 days | 0.012 [0.002, 0.018] |
| The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
Share and Cite
Senapati, A.; Mertel, A.; Schlechte-Welnicz, W.; Calabrese, J.M. Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions. Mathematics 2024 , 12 , 2065. https://doi.org/10.3390/math12132065
Senapati A, Mertel A, Schlechte-Welnicz W, Calabrese JM. Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions. Mathematics . 2024; 12(13):2065. https://doi.org/10.3390/math12132065
Senapati, Abhishek, Adam Mertel, Weronika Schlechte-Welnicz, and Justin M. Calabrese. 2024. "Estimating Cross-Border Mobility from the Difference in Peak Timing: A Case Study of Poland–Germany Border Regions" Mathematics 12, no. 13: 2065. https://doi.org/10.3390/math12132065
Article Metrics
Article access statistics, further information, mdpi initiatives, follow mdpi.

Subscribe to receive issue release notifications and newsletters from MDPI journals
- CBSE Class 10
CBSE Class 10 Syllabus 2024-25: Download Latest and Revised FREE PDFs
Cbse class 10 syllabus: the central board of secondary education (cbse) curriculum is out for the academic year 2024–25 on the official website, cbseacademic.nic.in. students and teachers can download the direct pdf of the latest and revised cbse class 10 syllabus 2025 here for maths, science, social science, hindi, english, and other elective subjects..

CBSE Syllabus 2025 for Class 10: The Central Board of Secondary Education (CBSE) 2024 board exams for Class 10 are over, and the new academic session has begun. This new syllabus or curriculum will be followed for the academic session 2024–25. In the CBSE-released syllabus, you will find the PDFs of the compulsory and optional subjects in free downloadable format.
The new syllabus for CBSE 10th is a new initiative to improve the classroom and school environment by encouraging the holistic development of students. According to CBSE, “the secondary education curriculum is a major step in giving shape to the nation’s vision of education. It aims to provide education that addresses local, national, and global needs.”
Here, the CBSE Class 10 syllabus 2024–25 is provided for Maths, Science, Social Science, Hindi, English, and other elective subjects in PDF format. You can scroll down and download the PDFs from the link provided below.
CBSE Class 10 Curriculum Areas
CBSE Class 10 Syllabus 2024-25
Here, you will get the subject-wise 2024 CBSE Class 10 syllabus. These syllabi are the latest and include all the revisions that CBSE would have thought of for the new academic year. Download these files and keep them for future reference.
CBSE Secondary School Curriculum Salient Features
- i. provide ample scope for holistic i.e., physical, intellectual and social development of students;
- ii. emphasize constructivist rather than rote learning by highlighting the importance of hands-on experience;
- iii. enlist general and specific teaching and assessment objectives to make learning competency-based and attain mastery over laid down competencies;
- iv. encourage the application of knowledge and skills in real-life problem-solving scenarios;
- v. uphold the ‘Constitutional Values’ by encouraging values-based learning activities;
- vi. promote 21st Century Skills, Life Skills, Financial Literacy, Digital Literacy, Health and Wellness, Road Safety, Citizenship Education, Disaster Management and multilingualism;
- vii. integrate innovations in pedagogy such as experiential, activity-centered, joyful learning, Sport & Art-Integrated Learning, toy-based pedagogy, storytelling, gamification etc. with technological innovations (ICT integration) to keep pace with the global trends in various disciplines;
- viii. promote inclusive practices as an overriding consideration in all educational activities;
- ix. enhance and support learning by different types of assessments; and
- x. strengthen knowledge and attitude related to livelihood skills;
- xi. foster multilingual and multicultural learning and national understanding in an interdependent society;
- xii. integrate environmental education in various disciplines from classes I- XII.
How to Download CBSE Class 10 Syllabus 2025?
The CBSE 2024–25 curriculum is out! Students and teachers can download the syllabus PDF for all the subjects by following the steps mentioned below:
Step 1: Visit the official website of the Central Board of Secondary Education (CBSE) at cbseacademic.nic.in.
Step 2: Click on the section labelled “Curriculum.”
Step 3: Click on the link or tab mentioning "Curriculum 2024-25."
Features of CBSE Class 10 Syllabus 2024-25
- The CBSE Class 10 syllabus is designed in such a that it help students know the latest question paper pattern.
- The typology of questions and their weightage is also provided through the syllabus.
- The syllabus involves all the topics and units with proper marking scheme.
- Simple language makes it easy to understand and comprehend.
- CBSE Class 10 Mock Test Videos For Quick Revision
- CBSE Class 10 Science Lab Manual PDF
Having the latest syllabus is mandatory and is the first resource you need to crack your board exams. Thus, students should always keep a copy of the syllabus with them.
- Easy Tips to Remember First 30 Elements of Periodic Table
- Atomic Mass And Molecular Mass of Elements
- Atomic Number and Mass Number
- Chemical Formula and Molecular Structure of Benzene
- CBSE Class 10 Syllabus 2023-24
- PCM, PCB or PCMB: Know Which Stream You Should Take in Class 11
- NCERT Books for Class 10 All Subjects PDF (2024-25)
Get here latest School , CBSE and Govt Jobs notification in English and Hindi for Sarkari Naukari and Sarkari Result . Download the Jagran Josh Sarkari Naukri App .
- Is CBSE Class 10 syllabus 2025 out? + Yes, the Central Board of Secondary Education (CBSE) has updated its curriculum section for the academic year 2024-25. Students can download the syllabus PDFs from CBSE's official website.
- Is there any change in CBSE Class 10 syllabus 2024-25? + The CBSE Board has not updated any information regarding the change in the Class 10 syllabus. It is advised for students to follow the 2025 syllabus for their 2024–25 academic session. After comparing the 2024 and 2025 syllabi, the detailed information will be updated on the official website of Jagran Josh.
- SSC Selection Post Answer Key 2024
- CTET Admit Card 2024
- SSC MTS 2024 Notification
- CTET July Admit Card 2024
- SSC CHSL Exam Analysis 2024
- NEET PG Exam Date 2024
- AP TET 2024 Notification
- APSC SO Result 2024
- APSC SO Admit Card 2024
- UPSC CSE Admit Card 2024
- Education News
Latest Education News
Upcoming ICC Tournaments List: आ गयी साल 2025 से 2031 तक की ICC टूर्नामेंट की लिस्ट, कब और कहां आयोजन, देखें यहां
KU Result 2024 OUT at kakatiya.ac.in; Direct Link to Download Kakatiya University UG and PG Marksheet
National Workshop on Blue Biotechnology 5th & 6th July 2024 Sponsored by Ministry of Earth Sciences
Calling All Da Vincis of Engineering: Invent the Future with the James Dyson Award
Brain Teaser: Only 1% With Sharp Attention To Detail Find The Mistake In This Park Scene In 12 Seconds!
Brain Teaser: Untangle the Animal Equation in Record Time!
What is the Difference Between Vintage and Antique? Know 3 Key differences
Picture Puzzle IQ Test: How Sharp Are Your Eyes? Find 2 Muffins Hidden Among These Cute Dogs In 15 Seconds!
Personality Test: Your Face Shape Reveals Your Hidden Personality Traits
Personality Test: Your Way Of Holding Your Phone Reveals Your Hidden Personality Traits
Optical Illusion IQ Test: Only 1% Intelligent Observers Can Spot The Oyster In 12 Seconds!
Optical Illusion IQ Test: Can You Spot The Turtle Hidden Among These Kittens In 12 Seconds?
Personality Test: Your Sleeping Position Reveals Your Hidden Personality Traits
Seek and Find Puzzle: Can You Find the Maple Leaf? It's a Hide-and-Seek IQ Test for Your Eyes!
Wimbledon Prize Money 2024: टी20 वर्ल्ड कप की तुलना में कितनी है विंबलडन 2024 की पुरस्कार राशि? अंतर देख हो जायेंगे हैरान
UK General Election Result 2024: भारतीय मूल के प्रमुख नेता जो ब्रिटेन में बने सांसद, देखें पूरी लिस्ट
IAS, IPS Salary in Hindi: जानें कितनी होती है आईएएस और आईपीएस अधिकारी की सैलरी?
[लिंक एक्टिव] CTET Admit Card 2024 OUT: सीटीईटी एडमिट कार्ड जारी, ctet.nic.in से तुरंत डाउनलोड करें हॉल टिकट
NEET UG Counselling 2024 Postponed Until Further Notice, Check Latest Updates Here
JEECUP Counselling 2024 Shedule Out, Round 1 Choice Filling Begin On July 12

IMAGES
VIDEO
COMMENTS
CBSE Board has introduced the case study questions for the ongoing academic session 2021-22. The board will ask the paper on the basis of a different exam pattern which has been introduced this year where 50% syllabus is occupied for MCQ for Term 1 exam. Selfstudys has provided below the chapter-wise questions for CBSE Class 10 Maths.
These Case Study and Passage Based questions are published by the experts of CBSE Experts for the students of CBSE Class 10 so that they can score 100% on Boards. CBSE Class 10 Mathematics Exam 2024 will have a set of questions based on case studies in the form of MCQs. The CBSE Class 10 Mathematics Question Bank on Case Studies, provided in ...
REAL NUMBERS- CASE STUDYCASE STUDY 1.To enhance the reading skills of grade X students, the school nominates you and two of. our friends to set up a class library. There are two sectio. s- section A and section B of grade X. There are 32 students. ection A and 36 students in sectionB.What is the minimum number of books you will acquire for the ...
CBSE Case Study Questions for Class 10 Maths - All Chapters. Tips to Solve Case Study Based Questions Accurately. CBSE Class 10 Maths Best & Complete Study Material for 2021-2022.
First of all, we would like to clarify that class 10 maths case study questions are subjective and CBSE will not ask multiple-choice questions in case studies. So, you must download the myCBSEguide app to get updated model question papers having new pattern subjective case study questions for class 10 the mathematics year 2022-23.
CBSE 10th Class Case Study for the Maths Subject is available here on this website. These Case studies can help the students to solve the different types of questions that are based on the case study or passage. CBSE Board will be asking case study questions based on Maths subjects in the upcoming board exams. Thus, it becomes an essential ...
QB365 Provides the updated CASE Study Questions for Class 10 Maths, and also provide the detail solution for each and every case study questions . Case study questions are latest updated question pattern from NCERT, QB365 will helps to get more marks in Exams
Case Study Questions Class 10 Maths PDF. In class 10 Board Exam 2021, You will find a new type of case-based questions. This is for the first time when you are going to face these type of questions in the board examination. CBSE has introduced these types of questions to better understand each chapter of class 10 maths.
These CBSE Class 10 Mathematics Case Studies have been developed by experienced teachers of schools.studyrate.in for the benefit of Class 10 students. Class 10th Science Case Study Questions; Benefits of Case Study Questions for Class 10 Mathematics. Case study questions offer several benefits to both students and teachers. Here are some key ...
Case-based questions are actually a great opportunity to showcase your problem-solving skills, provided your foundational concepts are strong. This blog post is your one-stop guide to mastering case studies in your upcoming Maths exam. The CBSE board format incorporates 3 case study questions, each worth a total of 4 marks (broken down as 1+1+2 ...
CBSE Class 10 Maths Important Case Study Questions. Related: CBSE Class 10 Maths Important Formulas for Last Minute Revision for Board Exam 2024. 1 Two Friends Geeta and Sita were playing near the ...
CBSE Class 10 Case Study Questions for Maths Chapter 5 - Arithmetic Progression are available here with answers. All the questions have been published by the CBSE board. Students must practice all ...
Now represent the following situations in the form of a quadratic equation. The sum of squares of two consecutive integers is 650. (a) x 2 + 2x - 650 = 0 (b) 2x 2 +2x - 649 = 0. (c) x 2 - 2x - 650 = 0 (d) 2x 2 + 6x - 550 = 0. Show Answer. The sum of two numbers is 15 and the sum of their reciprocals is 3/10. (a) x 2 + 10x - 150 = 0.
Question 1: Aanya and her father go to meet her friend Juhi for a party. When they reached to [uhi's place, Aanya saw the roof of the house, which is triangular in shape. If she imagined the dimensions of the roof as given in the figure, then answer the following questions. (ii) Measure of ∠A =. (iii) Measure of ∠C =.
Show Answer. (v) If A, B and C are three rational numbers such that 85C - 340A = 109, 425A + 85B = 146, then the sum of A, B and C is divisible by. (a) 3. (b) 6. (c) 7. (d) 9. Show Answer. Case Study 3: Real numbers are an essential concept in mathematics that encompasses both rational and irrational numbers.
Here, we have provided case-based/passage-based questions for Class 10 Maths Chapter 1 Real Numbers. Case Study/Passage-Based Questions. Question 1: Srikanth has made a project on real numbers, where he finely explained the applicability of exponential laws and divisibility conditions on real numbers. He also included some assessment questions ...
CBSE has recently added Case Study Based Questions or CSQ in Maths, Science and Social Science. You can visit this article to get to practice the official Sample Papers released by CBSE by clicking over here. Also do join out telegram channel to get all the updates and to participate in Quiz by clicking here.
CBSE 10th Maths Exam 2021 : Case Study Questions with Answers. In class 10th board exams 2021, students will observe new types of case study questions. For the first time, the board has introduced the case study questions in the board exam. we have provided the chapters-wise case study question with answers. 1.
Case Study Questions for Class 10 Maths Chapter 1 Real Numbers. Question 1: HCF and LCM are widely used in number system especially in real numbers in finding relationship between different numbers and their general forms. Also, product of two positive integers is equal to the product of their HCF and LCM. Based on the above information answer ...
Download case study question pdfs for CBSE Class 10th Maths, CBSE Class 10th English, CBSE Class 10th Sciece, CBSE Class 10th SST. As the CBSE 10th Term-1 Board Exams are approaching fast, you can use these worksheets for FREE for practice by students for the new case study formats for CBSE introduced this year.
Students looking for Case Study on Probability Class 10 Maths can use this page to download the PDF file. The case study questions on Probability are based on the CBSE Class 10 Maths Syllabus, and therefore, referring to the Probability case study questions enable students to gain the appropriate knowledge and prepare better for the Class 10 ...
You can check your knowledge by solving case study-based questions for Class 10 Maths Chapter 10 Circles. In CBSE Class 10 Maths Paper, Students will have to answer some questions based on Assertion and Reason. There will be a few questions based on case studies and passage-based as well. In that, a paragraph will be given, and then the MCQ ...
67 Likes, TikTok video from StudyStrategy101 (@studystrategy101): "important topics of Maths Class 10 #examtips #studytok #maths #cbse #federalboard #studystrategy101 #fypシ". original sound - StudyStrategy101.
CBSE Class 10 Maths Names of Units with Weightage for 2024-25. ... Also Read: CBSE Class 10 Maths Complete Study Material. Solving the NCERT questions helps to.
Finally, as a case study, we apply the method to some selected regions along the Poland-Germany border that are directly connected through multiple modes of transportation and quantify the cross-border fluxes from the COVID-19 cases data from 20 February to 20 June 2021. ... Math. Sci. Eng. 2022, 30, 609-634.
CBSE Class 10 Syllabus 2025: The new syllabus for CBSE Class 10 is out for the academic session 2024-25. Get here FREE PDF of the CBSE Class 10 Maths, Science, Social Science, Hindi, and English ...