
Hands-On Linear Programming: Optimization With Python
Table of Contents
What Is Linear Programming?
What is mixed-integer linear programming, why is linear programming important, linear programming with python, small linear programming problem, infeasible linear programming problem, unbounded linear programming problem, resource allocation problem, installing scipy and pulp, using scipy, linear programming resources, linear programming solvers.
Linear programming is a set of techniques used in mathematical programming , sometimes called mathematical optimization, to solve systems of linear equations and inequalities while maximizing or minimizing some linear function . It’s important in fields like scientific computing, economics, technical sciences, manufacturing, transportation, military, management, energy, and so on.
The Python ecosystem offers several comprehensive and powerful tools for linear programming. You can choose between simple and complex tools as well as between free and commercial ones. It all depends on your needs.
In this tutorial, you’ll learn:
- What linear programming is and why it’s important
- Which Python tools are suitable for linear programming
- How to build a linear programming model in Python
- How to solve a linear programming problem with Python
You’ll first learn about the fundamentals of linear programming. Then you’ll explore how to implement linear programming techniques in Python. Finally, you’ll look at resources and libraries to help further your linear programming journey.
Free Bonus: 5 Thoughts On Python Mastery , a free course for Python developers that shows you the roadmap and the mindset you’ll need to take your Python skills to the next level.
Linear Programming Explanation
In this section, you’ll learn the basics of linear programming and a related discipline, mixed-integer linear programming. In the next section , you’ll see some practical linear programming examples. Later, you’ll solve linear programming and mixed-integer linear programming problems with Python.
Imagine that you have a system of linear equations and inequalities. Such systems often have many possible solutions. Linear programming is a set of mathematical and computational tools that allows you to find a particular solution to this system that corresponds to the maximum or minimum of some other linear function.
Mixed-integer linear programming is an extension of linear programming. It handles problems in which at least one variable takes a discrete integer rather than a continuous value . Although mixed-integer problems look similar to continuous variable problems at first sight, they offer significant advantages in terms of flexibility and precision.
Integer variables are important for properly representing quantities naturally expressed with integers, like the number of airplanes produced or the number of customers served.
A particularly important kind of integer variable is the binary variable . It can take only the values zero or one and is useful in making yes-or-no decisions, such as whether a plant should be built or if a machine should be turned on or off. You can also use them to mimic logical constraints.
Linear programming is a fundamental optimization technique that’s been used for decades in science- and math-intensive fields. It’s precise, relatively fast, and suitable for a range of practical applications.
Mixed-integer linear programming allows you to overcome many of the limitations of linear programming. You can approximate non-linear functions with piecewise linear functions , use semi-continuous variables , model logical constraints, and more. It’s a computationally intensive tool, but the advances in computer hardware and software make it more applicable every day.
Often, when people try to formulate and solve an optimization problem, the first question is whether they can apply linear programming or mixed-integer linear programming.
Some use cases of linear programming and mixed-integer linear programming are illustrated in the following articles:
- Gurobi Optimization Case Studies
- Five Areas of Application for Linear Programming Techniques
The importance of linear programming, and especially mixed-integer linear programming, has increased over time as computers have gotten more capable, algorithms have improved, and more user-friendly software solutions have become available.
The basic method for solving linear programming problems is called the simplex method , which has several variants. Another popular approach is the interior-point method .
Mixed-integer linear programming problems are solved with more complex and computationally intensive methods like the branch-and-bound method , which uses linear programming under the hood. Some variants of this method are the branch-and-cut method , which involves the use of cutting planes , and the branch-and-price method .
There are several suitable and well-known Python tools for linear programming and mixed-integer linear programming. Some of them are open source, while others are proprietary. Whether you need a free or paid tool depends on the size and complexity of your problem as well as on the need for speed and flexibility.
It’s worth mentioning that almost all widely used linear programming and mixed-integer linear programming libraries are native to and written in Fortran or C or C++. This is because linear programming requires computationally intensive work with (often large) matrices. Such libraries are called solvers . The Python tools are just wrappers around the solvers.
Python is suitable for building wrappers around native libraries because it works well with C/C++. You’re not going to need any C/C++ (or Fortran) for this tutorial, but if you want to learn more about this cool feature, then check out the following resources:
- Building a Python C Extension Module
- CPython Internals
- Extending Python with C or C++
Basically, when you define and solve a model, you use Python functions or methods to call a low-level library that does the actual optimization job and returns the solution to your Python object.
Several free Python libraries are specialized to interact with linear or mixed-integer linear programming solvers:
- SciPy Optimization and Root Finding
In this tutorial, you’ll use SciPy and PuLP to define and solve linear programming problems.
Linear Programming Examples
In this section, you’ll see two examples of linear programming problems:
- A small problem that illustrates what linear programming is
- A practical problem related to resource allocation that illustrates linear programming concepts in a real-world scenario
You’ll use Python to solve these two problems in the next section .
Consider the following linear programming problem:
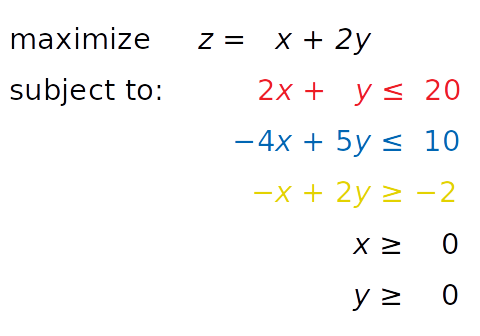
You need to find x and y such that the red, blue, and yellow inequalities, as well as the inequalities x ≥ 0 and y ≥ 0, are satisfied. At the same time, your solution must correspond to the largest possible value of z .
The independent variables you need to find—in this case x and y —are called the decision variables . The function of the decision variables to be maximized or minimized—in this case z —is called the objective function , the cost function , or just the goal . The inequalities you need to satisfy are called the inequality constraints . You can also have equations among the constraints called equality constraints .
This is how you can visualize the problem:
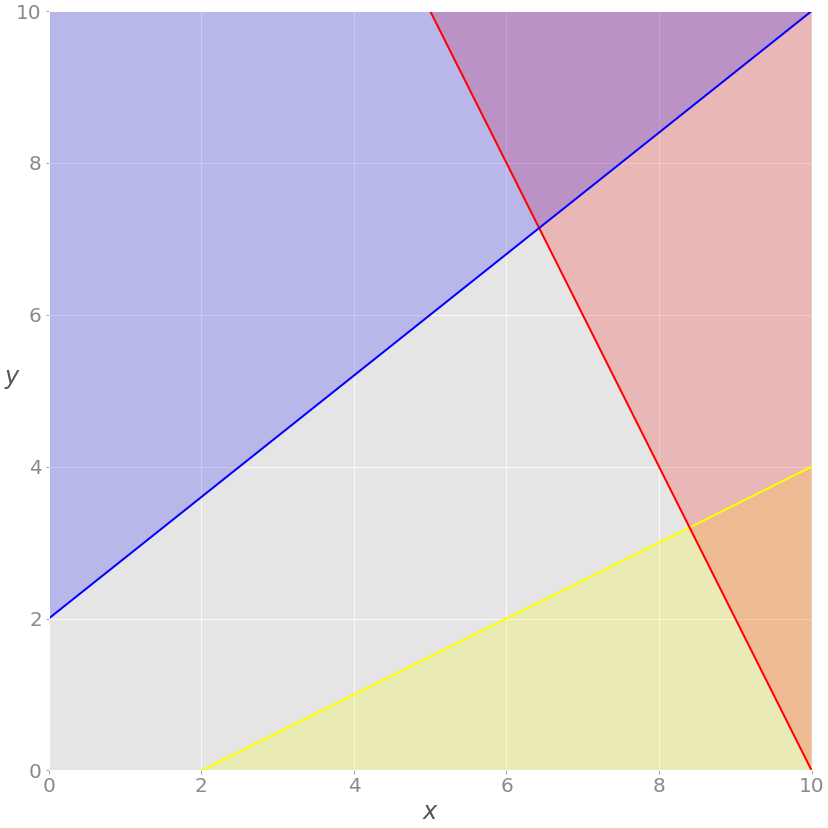
The red line represents the function 2 x + y = 20, and the red area above it shows where the red inequality is not satisfied. Similarly, the blue line is the function −4 x + 5 y = 10, and the blue area is forbidden because it violates the blue inequality. The yellow line is − x + 2 y = −2, and the yellow area below it is where the yellow inequality isn’t valid.
If you disregard the red, blue, and yellow areas, only the gray area remains. Each point of the gray area satisfies all constraints and is a potential solution to the problem. This area is called the feasible region , and its points are feasible solutions . In this case, there’s an infinite number of feasible solutions.
You want to maximize z . The feasible solution that corresponds to maximal z is the optimal solution . If you were trying to minimize the objective function instead, then the optimal solution would correspond to its feasible minimum.
Note that z is linear. You can imagine it as a plane in three-dimensional space. This is why the optimal solution must be on a vertex , or corner, of the feasible region. In this case, the optimal solution is the point where the red and blue lines intersect, as you’ll see later .
Sometimes a whole edge of the feasible region, or even the entire region, can correspond to the same value of z . In that case, you have many optimal solutions.
You’re now ready to expand the problem with the additional equality constraint shown in green:
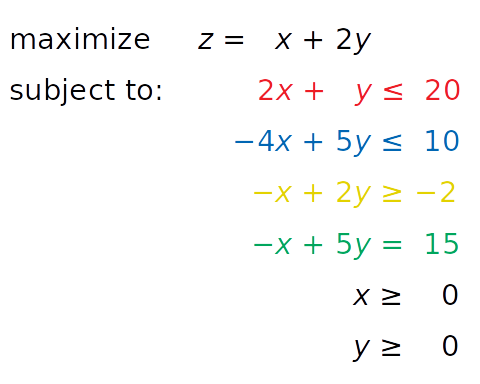
The equation − x + 5 y = 15, written in green, is new. It’s an equality constraint. You can visualize it by adding a corresponding green line to the previous image:
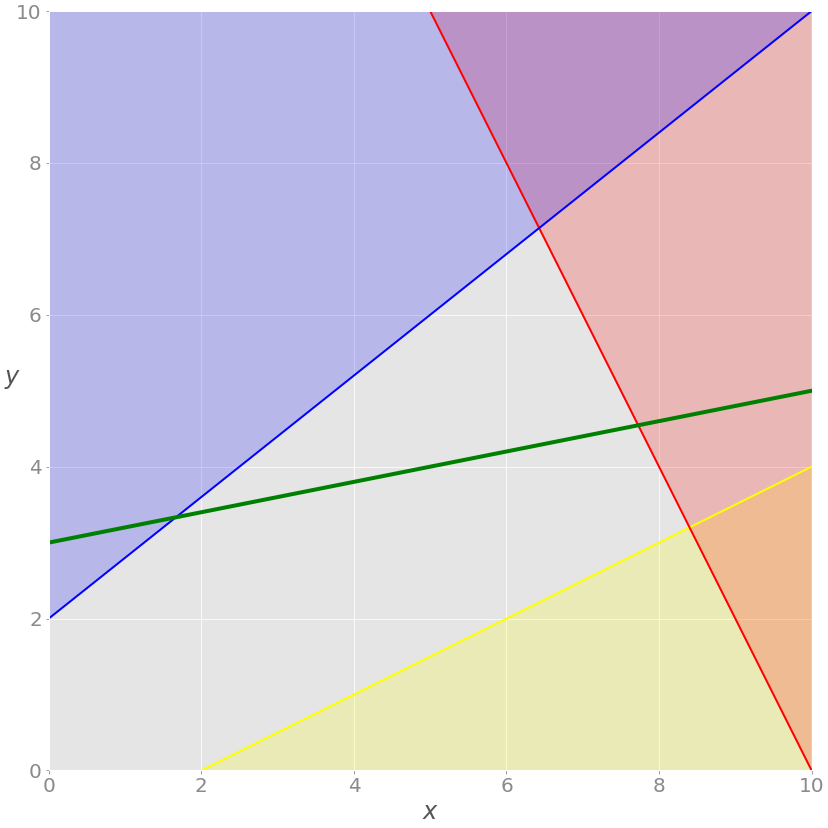
The solution now must satisfy the green equality, so the feasible region isn’t the entire gray area anymore. It’s the part of the green line passing through the gray area from the intersection point with the blue line to the intersection point with the red line. The latter point is the solution.
If you insert the demand that all values of x must be integers, then you’ll get a mixed-integer linear programming problem, and the set of feasible solutions will change once again:
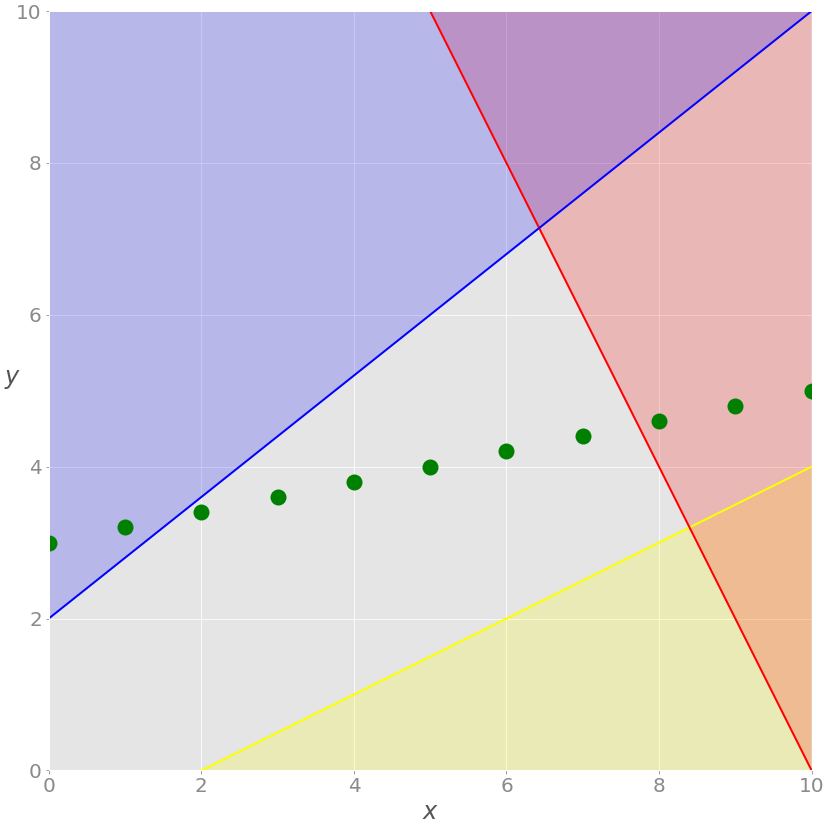
You no longer have the green line, only the points along the line where the value of x is an integer. The feasible solutions are the green points on the gray background, and the optimal one in this case is nearest to the red line.
These three examples illustrate feasible linear programming problems because they have bounded feasible regions and finite solutions.
A linear programming problem is infeasible if it doesn’t have a solution. This usually happens when no solution can satisfy all constraints at once.
For example, consider what would happen if you added the constraint x + y ≤ −1. Then at least one of the decision variables ( x or y ) would have to be negative. This is in conflict with the given constraints x ≥ 0 and y ≥ 0. Such a system doesn’t have a feasible solution, so it’s called infeasible.
Another example would be adding a second equality constraint parallel to the green line. These two lines wouldn’t have a point in common, so there wouldn’t be a solution that satisfies both constraints.
A linear programming problem is unbounded if its feasible region isn’t bounded and the solution is not finite. This means that at least one of your variables isn’t constrained and can reach to positive or negative infinity, making the objective infinite as well.
For example, say you take the initial problem above and drop the red and yellow constraints. Dropping constraints out of a problem is called relaxing the problem. In such a case, x and y wouldn’t be bounded on the positive side. You’d be able to increase them toward positive infinity, yielding an infinitely large z value.
In the previous sections, you looked at an abstract linear programming problem that wasn’t tied to any real-world application. In this subsection, you’ll find a more concrete and practical optimization problem related to resource allocation in manufacturing.
Say that a factory produces four different products, and that the daily produced amount of the first product is x ₁, the amount produced of the second product is x ₂, and so on. The goal is to determine the profit-maximizing daily production amount for each product, bearing in mind the following conditions:
The profit per unit of product is $20, $12, $40, and $25 for the first, second, third, and fourth product, respectively.
Due to manpower constraints, the total number of units produced per day can’t exceed fifty.
For each unit of the first product, three units of the raw material A are consumed. Each unit of the second product requires two units of the raw material A and one unit of the raw material B. Each unit of the third product needs one unit of A and two units of B. Finally, each unit of the fourth product requires three units of B.
Due to the transportation and storage constraints, the factory can consume up to one hundred units of the raw material A and ninety units of B per day.
The mathematical model can be defined like this:
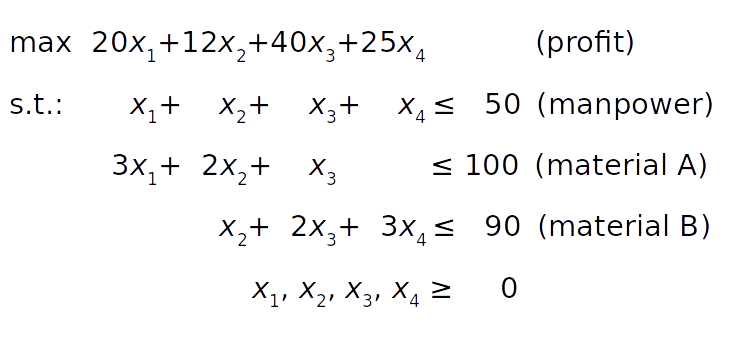
The objective function (profit) is defined in condition 1. The manpower constraint follows from condition 2. The constraints on the raw materials A and B can be derived from conditions 3 and 4 by summing the raw material requirements for each product.
Finally, the product amounts can’t be negative, so all decision variables must be greater than or equal to zero.
Unlike the previous example, you can’t conveniently visualize this one because it has four decision variables. However, the principles remain the same regardless of the dimensionality of the problem.
Linear Programming Python Implementation
In this tutorial, you’ll use two Python packages to solve the linear programming problem described above:
- SciPy is a general-purpose package for scientific computing with Python.
- PuLP is a Python linear programming API for defining problems and invoking external solvers.
SciPy is straightforward to set up. Once you install it, you’ll have everything you need to start. Its subpackage scipy.optimize can be used for both linear and nonlinear optimization .
PuLP allows you to choose solvers and formulate problems in a more natural way. The default solver used by PuLP is the COIN-OR Branch and Cut Solver (CBC) . It’s connected to the COIN-OR Linear Programming Solver (CLP) for linear relaxations and the COIN-OR Cut Generator Library (CGL) for cuts generation.
Another great open source solver is the GNU Linear Programming Kit (GLPK) . Some well-known and very powerful commercial and proprietary solutions are Gurobi , CPLEX , and XPRESS .
Besides offering flexibility when defining problems and the ability to run various solvers, PuLP is less complicated to use than alternatives like Pyomo or CVXOPT, which require more time and effort to master.
To follow this tutorial, you’ll need to install SciPy and PuLP. The examples below use version 1.4.1 of SciPy and version 2.1 of PuLP.
You can install both using pip :
You might need to run pulptest or sudo pulptest to enable the default solvers for PuLP, especially if you’re using Linux or Mac:
Optionally, you can download, install, and use GLPK. It’s free and open source and works on Windows, MacOS, and Linux. You’ll see how to use GLPK (in addition to CBC) with PuLP later in this tutorial.
On Windows, you can download the archives and run the installation files.
On MacOS, you can use Homebrew :
On Debian and Ubuntu, use apt to install glpk and glpk-utils :
On Fedora, use dnf with glpk-utils :
You might also find conda useful for installing GLPK:
After completing the installation, you can check the version of GLPK:
See GLPK’s tutorials on installing with Windows executables and Linux packages for more information.
In this section, you’ll learn how to use the SciPy optimization and root-finding library for linear programming.
To define and solve optimization problems with SciPy, you need to import scipy.optimize.linprog() :
Now that you have linprog() imported, you can start optimizing.
Let’s first solve the linear programming problem from above:
linprog() solves only minimization (not maximization) problems and doesn’t allow inequality constraints with the greater than or equal to sign (≥). To work around these issues, you need to modify your problem before starting optimization:
- Instead of maximizing z = x + 2 y, you can minimize its negative(− z = − x − 2 y).
- Instead of having the greater than or equal to sign, you can multiply the yellow inequality by −1 and get the opposite less than or equal to sign (≤).
After introducing these changes, you get a new system:
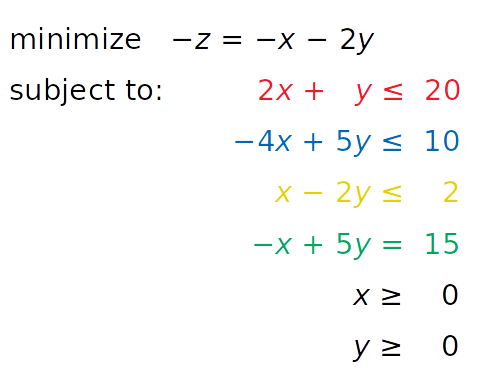
This system is equivalent to the original and will have the same solution. The only reason to apply these changes is to overcome the limitations of SciPy related to the problem formulation.
The next step is to define the input values:
You put the values from the system above into the appropriate lists, tuples , or NumPy arrays :
- obj holds the coefficients from the objective function.
- lhs_ineq holds the left-side coefficients from the inequality (red, blue, and yellow) constraints.
- rhs_ineq holds the right-side coefficients from the inequality (red, blue, and yellow) constraints.
- lhs_eq holds the left-side coefficients from the equality (green) constraint.
- rhs_eq holds the right-side coefficients from the equality (green) constraint.
Note: Please, be careful with the order of rows and columns!
The order of the rows for the left and right sides of the constraints must be the same. Each row represents one constraint.
The order of the coefficients from the objective function and left sides of the constraints must match. Each column corresponds to a single decision variable.
The next step is to define the bounds for each variable in the same order as the coefficients. In this case, they’re both between zero and positive infinity:
This statement is redundant because linprog() takes these bounds (zero to positive infinity) by default.
Note: Instead of float("inf") , you can use math.inf , numpy.inf , or scipy.inf .
Finally, it’s time to optimize and solve your problem of interest. You can do that with linprog() :
The parameter c refers to the coefficients from the objective function. A_ub and b_ub are related to the coefficients from the left and right sides of the inequality constraints, respectively. Similarly, A_eq and b_eq refer to equality constraints. You can use bounds to provide the lower and upper bounds on the decision variables.
You can use the parameter method to define the linear programming method that you want to use. There are three options:
- method="interior-point" selects the interior-point method. This option is set by default.
- method="revised simplex" selects the revised two-phase simplex method.
- method="simplex" selects the legacy two-phase simplex method.
linprog() returns a data structure with these attributes:
.con is the equality constraints residuals.
.fun is the objective function value at the optimum (if found).
.message is the status of the solution.
.nit is the number of iterations needed to finish the calculation.
.slack is the values of the slack variables, or the differences between the values of the left and right sides of the constraints.
.status is an integer between 0 and 4 that shows the status of the solution, such as 0 for when the optimal solution has been found.
.success is a Boolean that shows whether the optimal solution has been found.
.x is a NumPy array holding the optimal values of the decision variables.
You can access these values separately:
That’s how you get the results of optimization. You can also show them graphically:
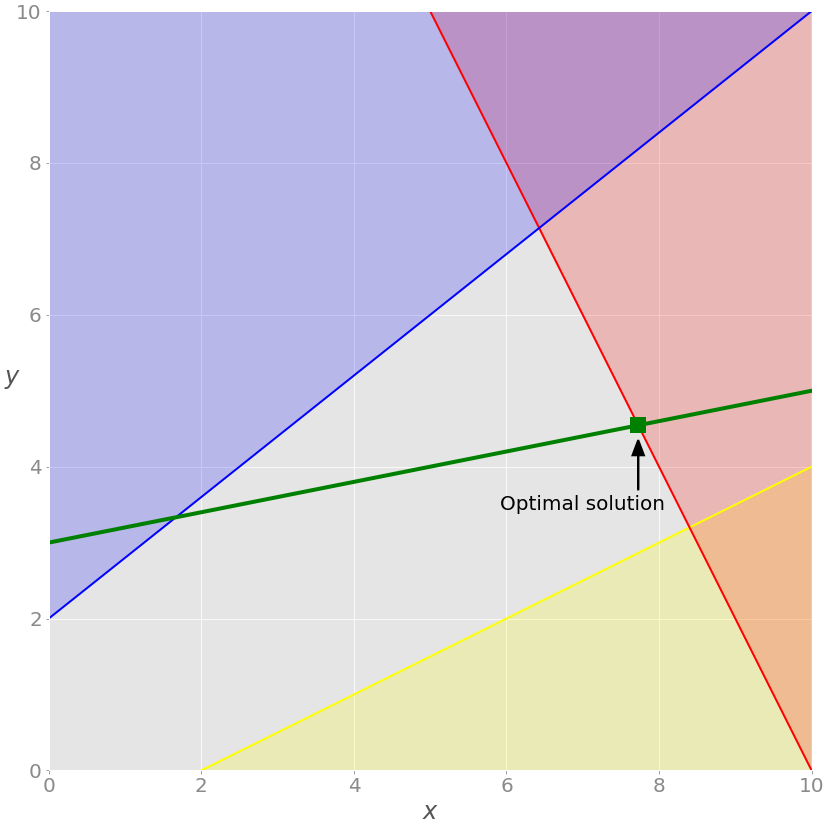
As discussed earlier, the optimal solutions to linear programming problems lie at the vertices of the feasible regions. In this case, the feasible region is just the portion of the green line between the blue and red lines. The optimal solution is the green square that represents the point of intersection between the green and red lines.
If you want to exclude the equality (green) constraint, just drop the parameters A_eq and b_eq from the linprog() call:
The solution is different from the previous case. You can see it on the chart:
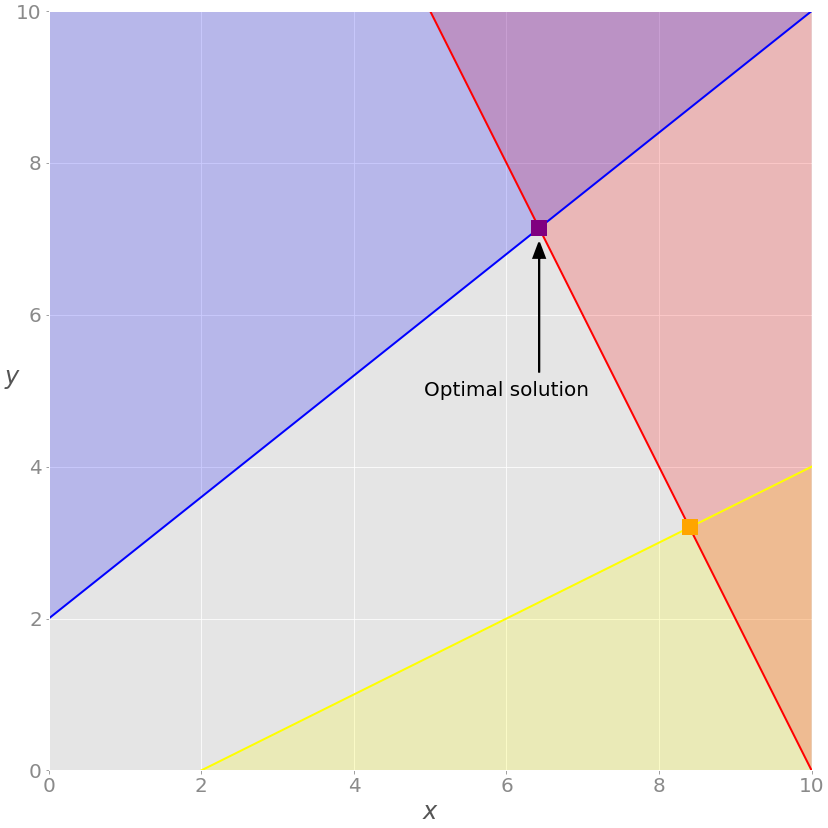
In this example, the optimal solution is the purple vertex of the feasible (gray) region where the red and blue constraints intersect. Other vertices, like the yellow one, have higher values for the objective function.
You can use SciPy to solve the resource allocation problem stated in the earlier section :
As in the previous example, you need to extract the necessary vectors and matrix from the problem above, pass them as the arguments to .linprog() , and get the results:
The result tells you that the maximal profit is 1900 and corresponds to x ₁ = 5 and x ₃ = 45. It’s not profitable to produce the second and fourth products under the given conditions. You can draw several interesting conclusions here:
The third product brings the largest profit per unit, so the factory will produce it the most.
The first slack is 0 , which means that the values of the left and right sides of the manpower (first) constraint are the same. The factory produces 50 units per day, and that’s its full capacity.
The second slack is 40 because the factory consumes 60 units of raw material A (15 units for the first product plus 45 for the third) out of a potential 100 units.
The third slack is 0 , which means that the factory consumes all 90 units of the raw material B. This entire amount is consumed for the third product. That’s why the factory can’t produce the second or fourth product at all and can’t produce more than 45 units of the third product. It lacks the raw material B.
opt.status is 0 and opt.success is True , indicating that the optimization problem was successfully solved with the optimal feasible solution.
SciPy’s linear programming capabilities are useful mainly for smaller problems. For larger and more complex problems, you might find other libraries more suitable for the following reasons:
SciPy can’t run various external solvers.
SciPy can’t work with integer decision variables.
SciPy doesn’t provide classes or functions that facilitate model building. You have to define arrays and matrices, which might be a tedious and error-prone task for large problems.
SciPy doesn’t allow you to define maximization problems directly. You must convert them to minimization problems.
SciPy doesn’t allow you to define constraints using the greater-than-or-equal-to sign directly. You must use the less-than-or-equal-to instead.
Fortunately, the Python ecosystem offers several alternative solutions for linear programming that are very useful for larger problems. One of them is PuLP, which you’ll see in action in the next section.
PuLP has a more convenient linear programming API than SciPy. You don’t have to mathematically modify your problem or use vectors and matrices. Everything is cleaner and less prone to errors.
As usual, you start by importing what you need:
Now that you have PuLP imported, you can solve your problems.
You’ll now solve this system with PuLP:
The first step is to initialize an instance of LpProblem to represent your model:
You use the sense parameter to choose whether to perform minimization ( LpMinimize or 1 , which is the default) or maximization ( LpMaximize or -1 ). This choice will affect the result of your problem.
Once that you have the model, you can define the decision variables as instances of the LpVariable class:
You need to provide a lower bound with lowBound=0 because the default value is negative infinity. The parameter upBound defines the upper bound, but you can omit it here because it defaults to positive infinity.
The optional parameter cat defines the category of a decision variable. If you’re working with continuous variables, then you can use the default value "Continuous" .
You can use the variables x and y to create other PuLP objects that represent linear expressions and constraints:
When you multiply a decision variable with a scalar or build a linear combination of multiple decision variables, you get an instance of pulp.LpAffineExpression that represents a linear expression.
Note: You can add or subtract variables or expressions, and you can multiply them with constants because PuLP classes implement some of the Python special methods that emulate numeric types like __add__() , __sub__() , and __mul__() . These methods are used to customize the behavior of operators like + , - , and * .
Similarly, you can combine linear expressions, variables, and scalars with the operators == , <= , or >= to get instances of pulp.LpConstraint that represent the linear constraints of your model.
Note: It’s also possible to build constraints with the rich comparison methods .__eq__() , .__le__() , and .__ge__() that define the behavior of the operators == , <= , and >= .
Having this in mind, the next step is to create the constraints and objective function as well as to assign them to your model. You don’t need to create lists or matrices. Just write Python expressions and use the += operator to append them to the model:
In the above code, you define tuples that hold the constraints and their names. LpProblem allows you to add constraints to a model by specifying them as tuples. The first element is a LpConstraint instance. The second element is a human-readable name for that constraint.
Setting the objective function is very similar:
Alternatively, you can use a shorter notation:
Now you have the objective function added and the model defined.
Note: You can append a constraint or objective to the model with the operator += because its class, LpProblem , implements the special method .__iadd__() , which is used to specify the behavior of += .
For larger problems, it’s often more convenient to use lpSum() with a list or other sequence than to repeat the + operator. For example, you could add the objective function to the model with this statement:
It produces the same result as the previous statement.
You can now see the full definition of this model:
The string representation of the model contains all relevant data: the variables, constraints, objective, and their names.
Note: String representations are built by defining the special method .__repr__() . For more details about .__repr__() , check out Pythonic OOP String Conversion: __repr__ vs __str__ or When Should You Use .__repr__() vs .__str__() in Python? .
Finally, you’re ready to solve the problem. You can do that by calling .solve() on your model object. If you want to use the default solver (CBC), then you don’t need to pass any arguments:
.solve() calls the underlying solver, modifies the model object, and returns the integer status of the solution, which will be 1 if the optimum is found. For the rest of the status codes, see LpStatus[] .
You can get the optimization results as the attributes of model . The function value() and the corresponding method .value() return the actual values of the attributes:
model.objective holds the value of the objective function, model.constraints contains the values of the slack variables, and the objects x and y have the optimal values of the decision variables. model.variables() returns a list with the decision variables:
As you can see, this list contains the exact objects that are created with the constructor of LpVariable .
The results are approximately the same as the ones you got with SciPy.
Note: Be careful with the method .solve() —it changes the state of the objects x and y !
You can see which solver was used by calling .solver :
The output informs you that the solver is CBC. You didn’t specify a solver, so PuLP called the default one.
If you want to run a different solver, then you can specify it as an argument of .solve() . For example, if you want to use GLPK and already have it installed, then you can use solver=GLPK(msg=False) in the last line. Keep in mind that you’ll also need to import it:
Now that you have GLPK imported, you can use it inside .solve() :
The msg parameter is used to display information from the solver. msg=False disables showing this information. If you want to include the information, then just omit msg or set msg=True .
Your model is defined and solved, so you can inspect the results the same way you did in the previous case:
You got practically the same result with GLPK as you did with SciPy and CBC.
Let’s peek and see which solver was used this time:
As you defined above with the highlighted statement model.solve(solver=GLPK(msg=False)) , the solver is GLPK.
You can also use PuLP to solve mixed-integer linear programming problems. To define an integer or binary variable, just pass cat="Integer" or cat="Binary" to LpVariable . Everything else remains the same:
In this example, you have one integer variable and get different results from before:
Now x is an integer, as specified in the model. (Technically it holds a float value with zero after the decimal point.) This fact changes the whole solution. Let’s show this on the graph:
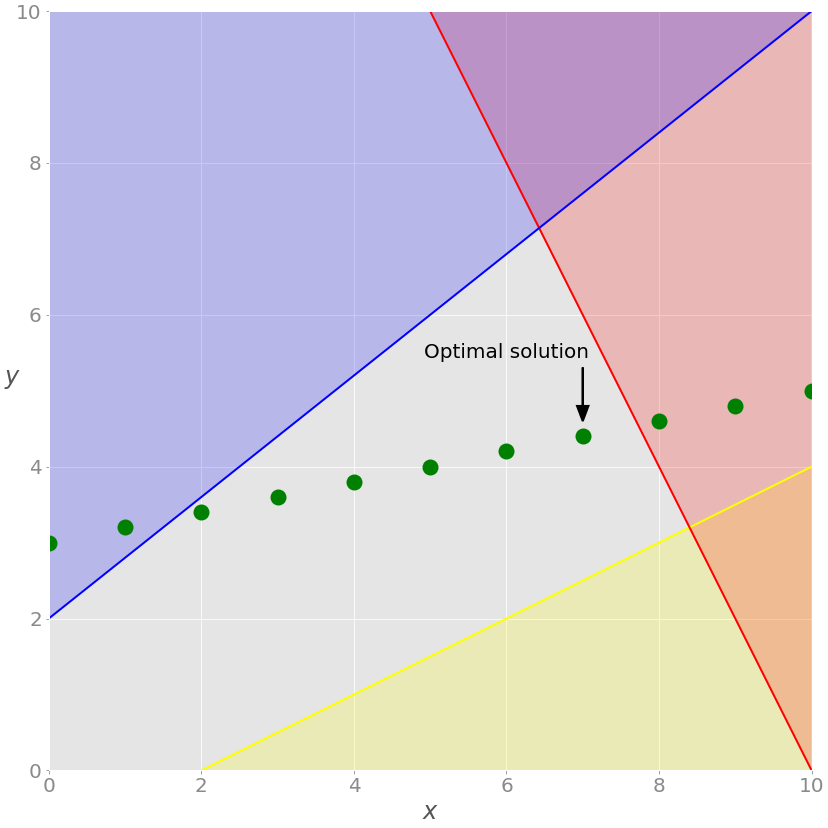
As you can see, the optimal solution is the rightmost green point on the gray background. This is the feasible solution with the largest values of both x and y , giving it the maximal objective function value.
GLPK is capable of solving such problems as well.
Now you can use PuLP to solve the resource allocation problem from above:
The approach for defining and solving the problem is the same as in the previous example:
In this case, you use the dictionary x to store all decision variables. This approach is convenient because dictionaries can store the names or indices of decision variables as keys and the corresponding LpVariable objects as values. Lists or tuples of LpVariable instances can be useful as well.
The code above produces the following result:
As you can see, the solution is consistent with the one obtained using SciPy. The most profitable solution is to produce 5.0 units of the first product and 45.0 units of the third product per day.
Let’s make this problem more complicated and interesting. Say the factory can’t produce the first and third products in parallel due to a machinery issue. What’s the most profitable solution in this case?
Now you have another logical constraint: if x ₁ is positive, then x ₃ must be zero and vice versa. This is where binary decision variables are very useful. You’ll use two binary decision variables, y ₁ and y ₃, that’ll denote if the first or third products are generated at all:
The code is very similar to the previous example except for the highlighted lines. Here are the differences:
Line 5 defines the binary decision variables y[1] and y[3] held in the dictionary y .
Line 12 defines an arbitrarily large number M . The value 100 is large enough in this case because you can’t have more than 100 units per day.
Line 13 says that if y[1] is zero, then x[1] must be zero, else it can be any non-negative number.
Line 14 says that if y[3] is zero, then x[3] must be zero, else it can be any non-negative number.
Line 15 says that either y[1] or y[3] is zero (or both are), so either x[1] or x[3] must be zero as well.
Here’s the solution:
It turns out that the optimal approach is to exclude the first product and to produce only the third one.
Linear programming and mixed-integer linear programming are very important topics. If you want to learn more about them—and there’s much more to learn than what you saw here—then you can find plenty of resources. Here are a few to get started with:
- Wikipedia Linear Programming Article
- Wikipedia Integer Programming Article
- MIT Introduction to Mathematical Programming Course
- Brilliant.org Linear Programming Article
- CalcWorkshop What Is Linear Programming?
- BYJU’S Linear Programming Article
Gurobi Optimization is a company that offers a very fast commercial solver with a Python API. It also provides valuable resources on linear programming and mixed-integer linear programming, including the following:
- Linear Programming (LP) – A Primer on the Basics
- Mixed-Integer Programming (MIP) – A Primer on the Basics
- Choosing a Math Programming Solver
If you’re in the mood to learn optimization theory, then there’s plenty of math books out there. Here are a few popular choices:
- Linear Programming: Foundations and Extensions
- Convex Optimization
- Model Building in Mathematical Programming
- Engineering Optimization: Theory and Practice
This is just a part of what’s available. Linear programming and mixed-integer linear programming are popular and widely used techniques, so you can find countless resources to help deepen your understanding.
Just like there are many resources to help you learn linear programming and mixed-integer linear programming, there’s also a wide range of solvers that have Python wrappers available. Here’s a partial list:
- SCIP with PySCIPOpt
- Gurobi Optimizer
Some of these libraries, like Gurobi, include their own Python wrappers. Others use external wrappers. For example, you saw that you can access CBC and GLPK with PuLP.
You now know what linear programming is and how to use Python to solve linear programming problems. You also learned that Python linear programming libraries are just wrappers around native solvers. When the solver finishes its job, the wrapper returns the solution status, the decision variable values, the slack variables, the objective function, and so on.
In this tutorial, you learned how to:
- Define a model that represents your problem
- Create a Python program for optimization
- Run the optimization program to find the solution to the problem
- Retrieve the result of optimization
You used SciPy with its own solver as well as PuLP with CBC and GLPK, but you also learned that there are many other linear programming solvers and Python wrappers. You’re now ready to dive into the world of linear programming!
If you have any questions or comments, then please put them in the comments section below.
🐍 Python Tricks 💌
Get a short & sweet Python Trick delivered to your inbox every couple of days. No spam ever. Unsubscribe any time. Curated by the Real Python team.

About Mirko Stojiljković

Mirko has a Ph.D. in Mechanical Engineering and works as a university professor. He is a Pythonista who applies hybrid optimization and machine learning methods to support decision making in the energy sector.
Each tutorial at Real Python is created by a team of developers so that it meets our high quality standards. The team members who worked on this tutorial are:

Master Real-World Python Skills With Unlimited Access to Real Python
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
Join us and get access to thousands of tutorials, hands-on video courses, and a community of expert Pythonistas:
What Do You Think?
What’s your #1 takeaway or favorite thing you learned? How are you going to put your newfound skills to use? Leave a comment below and let us know.
Commenting Tips: The most useful comments are those written with the goal of learning from or helping out other students. Get tips for asking good questions and get answers to common questions in our support portal . Looking for a real-time conversation? Visit the Real Python Community Chat or join the next “Office Hours” Live Q&A Session . Happy Pythoning!
Keep Learning
Related Topics: intermediate data-science
Keep reading Real Python by creating a free account or signing in:
Already have an account? Sign-In
Almost there! Complete this form and click the button below to gain instant access:

5 Thoughts On Python Mastery
🔒 No spam. We take your privacy seriously.
Linear programming: minimize a linear objective function subject to linear equality and inequality constraints.
Linear programming solves problems of the following form:
where \(x\) is a vector of decision variables; \(c\) , \(b_{ub}\) , \(b_{eq}\) , \(l\) , and \(u\) are vectors; and \(A_{ub}\) and \(A_{eq}\) are matrices.
Alternatively, that’s:
minimize c @ x such that A_ub @ x <= b_ub A_eq @ x == b_eq lb <= x <= ub
Note that by default lb = 0 and ub = None . Other bounds can be specified with bounds .
The coefficients of the linear objective function to be minimized.
The inequality constraint matrix. Each row of A_ub specifies the coefficients of a linear inequality constraint on x .
The inequality constraint vector. Each element represents an upper bound on the corresponding value of A_ub @ x .
The equality constraint matrix. Each row of A_eq specifies the coefficients of a linear equality constraint on x .
The equality constraint vector. Each element of A_eq @ x must equal the corresponding element of b_eq .
A sequence of (min, max) pairs for each element in x , defining the minimum and maximum values of that decision variable. If a single tuple (min, max) is provided, then min and max will serve as bounds for all decision variables. Use None to indicate that there is no bound. For instance, the default bound (0, None) means that all decision variables are non-negative, and the pair (None, None) means no bounds at all, i.e. all variables are allowed to be any real.
The algorithm used to solve the standard form problem. ‘highs’ (default), ‘highs-ds’ , ‘highs-ipm’ , ‘interior-point’ (legacy), ‘revised simplex’ (legacy), and ‘simplex’ (legacy) are supported. The legacy methods are deprecated and will be removed in SciPy 1.11.0.
If a callback function is provided, it will be called at least once per iteration of the algorithm. The callback function must accept a single scipy.optimize.OptimizeResult consisting of the following fields:
The current solution vector.
The current value of the objective function c @ x .
True when the algorithm has completed successfully.
The (nominally positive) values of the slack, b_ub - A_ub @ x .
The (nominally zero) residuals of the equality constraints, b_eq - A_eq @ x .
The phase of the algorithm being executed.
An integer representing the status of the algorithm.
0 : Optimization proceeding nominally.
1 : Iteration limit reached.
2 : Problem appears to be infeasible.
3 : Problem appears to be unbounded.
4 : Numerical difficulties encountered.
The current iteration number.
A string descriptor of the algorithm status.
Callback functions are not currently supported by the HiGHS methods.
A dictionary of solver options. All methods accept the following options:
Maximum number of iterations to perform. Default: see method-specific documentation.
Set to True to print convergence messages. Default: False .
Set to False to disable automatic presolve. Default: True .
All methods except the HiGHS solvers also accept:
A tolerance which determines when a residual is “close enough” to zero to be considered exactly zero.
Set to True to automatically perform equilibration. Consider using this option if the numerical values in the constraints are separated by several orders of magnitude. Default: False .
Set to False to disable automatic redundancy removal. Default: True .
Method used to identify and remove redundant rows from the equality constraint matrix after presolve. For problems with dense input, the available methods for redundancy removal are:
Repeatedly performs singular value decomposition on the matrix, detecting redundant rows based on nonzeros in the left singular vectors that correspond with zero singular values. May be fast when the matrix is nearly full rank.
Uses the algorithm presented in [5] to identify redundant rows.
Uses a randomized interpolative decomposition. Identifies columns of the matrix transpose not used in a full-rank interpolative decomposition of the matrix.
Uses “svd” if the matrix is nearly full rank, that is, the difference between the matrix rank and the number of rows is less than five. If not, uses “pivot”. The behavior of this default is subject to change without prior notice.
Default: None. For problems with sparse input, this option is ignored, and the pivot-based algorithm presented in [5] is used.
For method-specific options, see show_options('linprog') .
Guess values of the decision variables, which will be refined by the optimization algorithm. This argument is currently used only by the ‘revised simplex’ method, and can only be used if x0 represents a basic feasible solution.
Indicates the type of integrality constraint on each decision variable.
0 : Continuous variable; no integrality constraint.
1 : Integer variable; decision variable must be an integer within bounds .
2 : Semi-continuous variable; decision variable must be within bounds or take value 0 .
3 : Semi-integer variable; decision variable must be an integer within bounds or take value 0 .
By default, all variables are continuous.
For mixed integrality constraints, supply an array of shape c.shape . To infer a constraint on each decision variable from shorter inputs, the argument will be broadcasted to c.shape using np.broadcast_to .
This argument is currently used only by the 'highs' method and ignored otherwise.
A scipy.optimize.OptimizeResult consisting of the fields below. Note that the return types of the fields may depend on whether the optimization was successful, therefore it is recommended to check OptimizeResult.status before relying on the other fields:
The values of the decision variables that minimizes the objective function while satisfying the constraints.
The optimal value of the objective function c @ x .
The (nominally positive) values of the slack variables, b_ub - A_ub @ x .
True when the algorithm succeeds in finding an optimal solution.
An integer representing the exit status of the algorithm.
0 : Optimization terminated successfully.
The total number of iterations performed in all phases.
A string descriptor of the exit status of the algorithm.
Additional options accepted by the solvers.
This section describes the available solvers that can be selected by the ‘method’ parameter.
‘highs-ds’ and ‘highs-ipm’ are interfaces to the HiGHS simplex and interior-point method solvers [13] , respectively. ‘highs’ (default) chooses between the two automatically. These are the fastest linear programming solvers in SciPy, especially for large, sparse problems; which of these two is faster is problem-dependent. The other solvers ( ‘interior-point’ , ‘revised simplex’ , and ‘simplex’ ) are legacy methods and will be removed in SciPy 1.11.0.
Method highs-ds is a wrapper of the C++ high performance dual revised simplex implementation (HSOL) [13] , [14] . Method highs-ipm is a wrapper of a C++ implementation of an i nterior- p oint m ethod [13] ; it features a crossover routine, so it is as accurate as a simplex solver. Method highs chooses between the two automatically. For new code involving linprog , we recommend explicitly choosing one of these three method values.
Added in version 1.6.0.
Method interior-point uses the primal-dual path following algorithm as outlined in [4] . This algorithm supports sparse constraint matrices and is typically faster than the simplex methods, especially for large, sparse problems. Note, however, that the solution returned may be slightly less accurate than those of the simplex methods and will not, in general, correspond with a vertex of the polytope defined by the constraints.
Added in version 1.0.0.
Method revised simplex uses the revised simplex method as described in [9] , except that a factorization [11] of the basis matrix, rather than its inverse, is efficiently maintained and used to solve the linear systems at each iteration of the algorithm.
Added in version 1.3.0.
Method simplex uses a traditional, full-tableau implementation of Dantzig’s simplex algorithm [1] , [2] ( not the Nelder-Mead simplex). This algorithm is included for backwards compatibility and educational purposes.
Added in version 0.15.0.
Before applying interior-point , revised simplex , or simplex , a presolve procedure based on [8] attempts to identify trivial infeasibilities, trivial unboundedness, and potential problem simplifications. Specifically, it checks for:
rows of zeros in A_eq or A_ub , representing trivial constraints;
columns of zeros in A_eq and A_ub , representing unconstrained variables;
column singletons in A_eq , representing fixed variables; and
column singletons in A_ub , representing simple bounds.
If presolve reveals that the problem is unbounded (e.g. an unconstrained and unbounded variable has negative cost) or infeasible (e.g., a row of zeros in A_eq corresponds with a nonzero in b_eq ), the solver terminates with the appropriate status code. Note that presolve terminates as soon as any sign of unboundedness is detected; consequently, a problem may be reported as unbounded when in reality the problem is infeasible (but infeasibility has not been detected yet). Therefore, if it is important to know whether the problem is actually infeasible, solve the problem again with option presolve=False .
If neither infeasibility nor unboundedness are detected in a single pass of the presolve, bounds are tightened where possible and fixed variables are removed from the problem. Then, linearly dependent rows of the A_eq matrix are removed, (unless they represent an infeasibility) to avoid numerical difficulties in the primary solve routine. Note that rows that are nearly linearly dependent (within a prescribed tolerance) may also be removed, which can change the optimal solution in rare cases. If this is a concern, eliminate redundancy from your problem formulation and run with option rr=False or presolve=False .
Several potential improvements can be made here: additional presolve checks outlined in [8] should be implemented, the presolve routine should be run multiple times (until no further simplifications can be made), and more of the efficiency improvements from [5] should be implemented in the redundancy removal routines.
After presolve, the problem is transformed to standard form by converting the (tightened) simple bounds to upper bound constraints, introducing non-negative slack variables for inequality constraints, and expressing unbounded variables as the difference between two non-negative variables. Optionally, the problem is automatically scaled via equilibration [12] . The selected algorithm solves the standard form problem, and a postprocessing routine converts the result to a solution to the original problem.
Dantzig, George B., Linear programming and extensions. Rand Corporation Research Study Princeton Univ. Press, Princeton, NJ, 1963
Hillier, S.H. and Lieberman, G.J. (1995), “Introduction to Mathematical Programming”, McGraw-Hill, Chapter 4.
Bland, Robert G. New finite pivoting rules for the simplex method. Mathematics of Operations Research (2), 1977: pp. 103-107.
Andersen, Erling D., and Knud D. Andersen. “The MOSEK interior point optimizer for linear programming: an implementation of the homogeneous algorithm.” High performance optimization. Springer US, 2000. 197-232.
Andersen, Erling D. “Finding all linearly dependent rows in large-scale linear programming.” Optimization Methods and Software 6.3 (1995): 219-227.
Freund, Robert M. “Primal-Dual Interior-Point Methods for Linear Programming based on Newton’s Method.” Unpublished Course Notes, March 2004. Available 2/25/2017 at https://ocw.mit.edu/courses/sloan-school-of-management/15-084j-nonlinear-programming-spring-2004/lecture-notes/lec14_int_pt_mthd.pdf
Fourer, Robert. “Solving Linear Programs by Interior-Point Methods.” Unpublished Course Notes, August 26, 2005. Available 2/25/2017 at http://www.4er.org/CourseNotes/Book%20B/B-III.pdf
Andersen, Erling D., and Knud D. Andersen. “Presolving in linear programming.” Mathematical Programming 71.2 (1995): 221-245.
Bertsimas, Dimitris, and J. Tsitsiklis. “Introduction to linear programming.” Athena Scientific 1 (1997): 997.
Andersen, Erling D., et al. Implementation of interior point methods for large scale linear programming. HEC/Universite de Geneve, 1996.
Bartels, Richard H. “A stabilization of the simplex method.” Journal in Numerische Mathematik 16.5 (1971): 414-434.
Tomlin, J. A. “On scaling linear programming problems.” Mathematical Programming Study 4 (1975): 146-166.
Huangfu, Q., Galabova, I., Feldmeier, M., and Hall, J. A. J. “HiGHS - high performance software for linear optimization.” https://highs.dev/
Huangfu, Q. and Hall, J. A. J. “Parallelizing the dual revised simplex method.” Mathematical Programming Computation, 10 (1), 119-142, 2018. DOI: 10.1007/s12532-017-0130-5
Consider the following problem:
The problem is not presented in the form accepted by linprog . This is easily remedied by converting the “greater than” inequality constraint to a “less than” inequality constraint by multiplying both sides by a factor of \(-1\) . Note also that the last constraint is really the simple bound \(-3 \leq x_1 \leq \infty\) . Finally, since there are no bounds on \(x_0\) , we must explicitly specify the bounds \(-\infty \leq x_0 \leq \infty\) , as the default is for variables to be non-negative. After collecting coeffecients into arrays and tuples, the input for this problem is:
The marginals (AKA dual values / shadow prices / Lagrange multipliers) and residuals (slacks) are also available.
For example, because the marginal associated with the second inequality constraint is -1, we expect the optimal value of the objective function to decrease by eps if we add a small amount eps to the right hand side of the second inequality constraint:
Also, because the residual on the first inequality constraint is 39, we can decrease the right hand side of the first constraint by 39 without affecting the optimal solution.
Integer Programming in Python
Freddy Boulton
Towards Data Science
Integer Programming (IP) problems are optimization problems where all of the variables are constrained to be integers. IP problems are useful mathematical models for how to best allocate one’s resources. Let’s say you’re organizing a marketing campaign for a political candidate and you’re deciding which constituents to send marketing materials to. You can send each constituent a catchy flyer, a detailed pamphlet explaining your agenda, or a bumper sticker (or a combination of the three). If you had a way to measure how likely someone is to vote for your candidate based on the marketing materials they received, how would you decide which materials to send while also being mindful to not exceed your supply?
Traditional optimization algorithms assume the variables can take on floating point values, but in our case, it isn’t reasonable to send someone half a bumper sticker or three quarters of a pamphlet. We’ll use a special python package called cvxpy to solve our problem such that the solutions make sense.
I’ll show you how to use cvxpy to solve the political candidate problem, but I’ll start first a simpler problem called the knapsack problem to show you how the cvxpy syntax works.
The Knapsack Problem
Let’s pretend you’re going on a hike and you’re planning which objects you can take with you. Each object has a weight in pounds w_i and will give you u_i units of utility. You’d like to take all of them but your knapsack can only carry P pounds. Suppose you can either take an object or not. Your goal is to maximize your utility without exceeding the weight limit of your bag.
A cvxpy problem has three parts:
- Creating the variable: We will represent our choice mathematically with a vector of 1’s and 0’s. A 1 will mean we’ve selected that object and a 0 will mean we’ve left it home. We construct a variable that can only take 1’s and 0’s with the cvxpy.Bool object.
- Specifying the constraints: We only need to make sure that the sum of our objects doesn’t exceed the weight limit P. We can compute the total weight of our objects with the dot product of the selection vector and the weights vector. Note that cvxpy overloads the * operator to perform matrix multiplication.
- Formulating the objective function: We want to find the selection that maximizes our utility. The utility of any given selection is the dot product of the selection vector and the utility vector.
Once we have a cost function and constraints, we pass them to a cvxpy Problem object. In this case, we’ve told cvxpy that we’re trying to maximize utility with cvxpy.Maximize. To solve the problem, we just have to run the solve method of our problem object. Afterwards, we can inspect the optimal value of our selection vector by looking at its value attribute.
We’ve selected the first four items and the sixth one. This makes sense because these have high ratio of utility to weight without weighing too much.
The Marketing Problem
Now that we’ve covered basic cvxpy syntax, we can solve the marketing optimization problem for our political candidate. Let’s say we had a model that takes in a constituent’s attributes and predicts the probability they will vote for our candidate for each combination of marketing materials we send them. I’m using fake data here but let’s pretend the model outputs the following probabilities:
There are eight total probabilities per constituent because there are eight total combinations of materials we could send an individual. Here’s what the entries of each 1 x 8 vector represent:
[1 flyer, 1 pamphlet, 1 bumper sticker, flyer and pamphlet, flyer and bumper sticker, pamphlet and bumper sticker, all three, none].
For example, the first constituent has a 0.0001 probability of voting for our candidate if he received a flyer or pamphlet, but a 0.3 probability of voting for our candidate if we sent him a bumper sticker.
Before we get into the cvxpy code, we’ll turn these probabilities into costs by taking the negative log. This makes the math work out nicer and it has a nice interpretation: if the probability is close to 1, the negative log will be close to 0. This means that there is little cost in sending that particular combination of materials to that constituent since we are certain it will lead them to vote for our candidate. Vice versa if the probability is close to 0.
Finally, let’s say that we cannot send more than 150 flyers, 80 pamphlets, and 25 bumper stickers.
Now that we’ve done all the set-up, we can get to the fun part:
- Creating the variable: We’ll use a cvxpy.Bool object again because we can only make binary choices here. We’ll specify that it must be the same shape as our probability matrix:
2. Specifying the constraints: Our selection variable will only tell us which of the 8 choices we’ve made for each constituent, but it won’t tell how many total materials we’ve decided to send to them. We need a way to turn our 1 x 8 selection vector into a 1 x 3 vector. We can do so by multiplying by the selection vector by the following matrix:
If this part is a little confusing, work out the following example:
The fourth entry of our decision vector represents sending a flyer and pamphlet to the constituent and multiplying by TRANSFORMER tells us just that! So we’ll tell cvxpy that multiplying our selection matrix by transformer can’t exceed our supply:
I’m summing over the rows with cvxpy.sum_entries to aggregate the total number of materials we’ve sent across all constituents.
We also need to ensure we’re making exactly once choice per constituent, otherwise the solver can attain zero cost by not sending anyone anything.
3. Formulating the objective function: The total cost of our assignment will be the sum of the costs we’ve incurred for each constituent. We’ll use the cvxpy.mul_elemwise function to multiply our selection matrix with our cost matrix, this will select the cost for each constituent, and the cvxpy.sum_elemwise function will compute the total cost by adding up the individual costs.
The final step is to create the cvxpy.Problem and solve it.
That’s it! Below is a snapshot of what our final assignments look like. We decided not to send any materials to the first constituent. This makes sense because the probability of them voting for our candidate is 0.3 whether we send them a bumper sticker or nothing at all.
It also turns out that the optimal assignment exhausts our supply of pamphlets and bumper stickers but only uses 83 of the total 150 flyers. We should tell our candidate that her flyers aren’t as persuasive as she thinks.
Here is all the code packaged together:
Closing Remarks
I hope you’ve enjoyed learning about integer programming problems and how to solve them in Python. Believe it or not, we’ve covered about 80% of the cvxpy knowledge you need to go out and solve your own optimization problems. I encourage you to read the official documentation to learn about the remaining 20%. CVXPY can solve more than just IP problems, check out their tutorials page to see what other problems cvxpy can solve.
To install cvxpy, follow the directions on their website. I would also install cvxopt to make sure all the solvers that come packaged with cvxpy will work on your machine
We’ve specified that cvxpy should use the GLPK_MI solver in the solve method. This is a special solver designed for IP problems. Before you solve your own problem, consult this table to see which prepackaged cvpxy solver is best suited to your problem.
Happy optimizing!

Written by Freddy Boulton
Data Scientist & Software Engineer
Text to speech
Implementation of a Integer Linear Programming Solver in Python
Introduction.
Integer linear programming problems are common in many domains. I recently found myself experimenting with formulating a probem as an integer programming problem, and I realized that I didn't really understand how the various solvers worked, so I set out to implement my own. This post is about the three pieces that need to be assembled to create one:
- Expression trees and rewrite rules to provide a convenient interface.
- Linear programming relaxation to get a non-integer solution (using scipy.optimize.linprog ).
- Branch-and-bound to refine the relaxed soltion to an integer solution.
You can follow along at [cwpearson/csips][https://github.com/cwpearson/csips]
Problem Formulation
A linear programming problem is an optimization problem with the following form:
find \(\mathbf{x}\) to maximize $$ \mathbf{c}^T\mathbf{x} $$
$$\begin{aligned} A\mathbf{x} &\leq \mathbf{b} \cr 0 &\leq \mathbf{x} \cr \end{aligned}$$
For integer linear programming (ILP) , there is one additional constrait:
$$ \mathbf{x} \in \mathbb{Z} $$
In plain english, \(\mathbf{x}\) is a vector, where each entry represents a variable we want to find the optimal value for. \(\mathbf{c}\) is a vector with one weight for each entry of \(\mathbf{x}\). We're trying to maximize the dot product \(\mathbf{c}^T\mathbf{x}\); we're just summing up each each entry of entry of \(\mathbf{x}\) weighted by the corresponding entry of \(\mathbf{c}\). For example, if we seek to maximize the sum of the first two entries of \(\mathbf{x}\), the first two entries of \(\mathbf{c}\) will be \(1\) and the rest \(0\).
What about Minimizing instead of Maximizing? Just maximize \(-\mathbf{c}^T\mathbf{x}\) instead of maximizing \(\mathbf{c}^T\mathbf{x}\).
What if one of my variables needs to be negative? At first glance, it appears \(0 \leq \mathbf{x}\) will be a problem. However, we'll just construct \(A\) and \(\mathbf{b}\) so that all constraints are relative to \(-\mathbf{x}_i\) instead of \(\mathbf{x}_i\) for variable \(i\).
To specify our problem, we must specify \(A\), \(\mathbf{b}\), and \(\mathbf{c}^T\).
For simple problems it might be convenient enough to do this unassisted, for example (pdf) :
find \(x,y\) to maximize $$ 4x + 5y $$
$$\begin{aligned} x + 4y &\leq 10 \cr 3x - 4y &\leq 6 \cr 0 &\leq x,y \end{aligned}$$
We have two variables \(x\) and \(y\), so Our \(\mathbf{x}\) vector will be two entries, \(\mathbf{x}_0\) for \(x\) and \(\mathbf{x}_1\) for \(y\). Correspondingly, \(A\) will have two columns, one for each variable, and our \(\mathbf{c}\) will have two entries, one for each variable. We have two constraints, so our \(A\) will have two rows, one for each constraint.
How do we handle \(0 \leq x,y\)? We'll cover that later when we talk about scipy's linprog function to actually solve this.
User-friendly Interface
- Implemented in expr.py
If your problem is complicated it can get clumsy to specify every constraint and objective in this form, since you'llneed to massage all your constraints so that all the variables are on the left and are \(\leq\) a constant on the right. It would be best to have the computer do this for you, and present a more natural interface akin to the following:
To do this, we'll introduce some python classes to represent nodes in an expression tree of our constraints. Then we'll overload the * , + , - , == , <= , and >= operators on those classes to allow those nodes to be composed into a tree from a natural expression.
For example, an implementation of scaling a variable by an integer:
Using part of the constraints above:
which represents variable x[0] multiplied by integer 3 . We can construct more complicated trees to support our expression grammar by extending these classes with additional operations (e.g. __leq__ , __sum__ , ...) and additional classes to represent summation expressions, less-or-equal equations, and so forth.
Conversion to Standard Form
- Implemented at csips.py
Once each constraint (and the objective) are represented as expression trees, the challenge then becomes converting them into the standard form, e.g. all variables and scalar multiplications on the left-hand side (a row of \(A\)), and a single constant on the right-hand side (an entry of \(\mathbf{b}\)). We can use a few rewrite rules to transform our expression trees into what we want.
Distribution: $$ a \times (b + c) \rightarrow a \times b + a \times c $$
Fold: $$ a + b \rightarrow c $$
Move left $$ a \leq b + c \rightarrow a - b \leq c $$
Flip: $$ a \geq b \rightarrow -a \leq -b $$
By applying these rules, we can convert any of our expressions to one where a sum of scaled variables is on the left hand side of \(\leq\), and a single int is on the right hand side. Then it's a simple matter of generating an \(\mathbf{x}\) with one entry per unique variable, \(A\) from the scaling on those variables, and \(\mathbf{b}\) from the right-hand side.
Linear Program Relaxation
The way this is usually done is actually by initially ignoring the integer constraint ( \(\mathbf{x} \in \mathbb{Z}\) ), then going back and "fixing" the non-integer parts of your solution. When you ignore the integer constraint, you're doing what's called "linear programming relaxation" (LP relaxation) . Solving the LP relaxation will provide a (possibly non-integer) \(\mathbf{x}\).
We'll use scipy's linprog function to solve the LP relaxation.
Here's how linprog 's arguments map to our formulation
- c : this is \(\mathbf{c}^T\)
- A_ub : this is \(A\)
- b_ub : this is \(\mathbf{b}\)
linprog also allows us to specify bounds on \(\mathbf{x}\) in a convenient form.
- bounds : this allows us to provide bounds on \(\mathbf{x}\), e.g. providing the tuple (0, None) implements \(0 \leq \mathbf{x}\). This is not strictly necessary since we can directly express this constraint using A_ub and b_ub .
linprog also allows us to specify additional constraints in the form \(A\mathbf{x} = \mathbf{b}\). This is not strictly necessary, since for a variable \(i\) we could just say \(\mathbf{x}_i \leq c\) and \(-\mathbf{x}_i \leq -c\) in our original formulation to achieve \(\mathbf{x}_i = c\).
- A_eq : \(A\) in optional \(A\mathbf{x} = \mathbf{b}\)
- b_eq : \(\mathbf{b}\) in optional \(A\mathbf{x} = \mathbf{b}\)
linprog will dutifully report the optimal solution as \(x = 4\), \(y = 1.5\), and \(4x \times 5y = 23.5\). Of course, \(y = 1.5\) is not an integer, so we'll use "branch and bound" to refine towards an integer solution.
Branch and Bound
Branch and bound is a whole family of algorithms for solving discrete and combinatorial optimization problems. It represents the space of solutions in a tree, where the root node is all possible solutions. Each node branches into two child nodes each which represents two non-overlapping smaller subsets of the full solution space. As the tree is descended, the solution space will either shrink to 1 (a feasible solution) or 0 (no feasible solution). As we discover feasible solutions, we will keep track of the best one. At any point, we may be able to determine a bound on the best possible solution offered by a subset. If that bound is worse than the best solution so far, we can skip that entire subtree.
For our ILP problem, the algorithm looks like this:
- Initialize the best objective observed so far to \(\inf\)
- Find the LP relaxation solution
- If the LP relaxation objective is worse than the best solution so far, discard it. The integer solution will be no better than the relaxation solution, so if the relaxation solution is worse, then the integer solution will be too.
- Else, push that solution onto a stack
- Take solution off the stack
- If all \(\mathbf{x}\) entries are integers and the objective is the best so far, record it
- Else, branch to produce two child nodes. If \(\mathbf{x}_i = c\) is non-integer, two subproblems, each with one additional constraint \(\mathbf{x}_i \leq \lfloor c \rfloor \) and \(\mathbf{x}_i \geq \lceil c \rceil \)
- Report the solution with the best result so far.
Doing so for our example will converge on a solution of \(x = 2\), \(y = 2\), and \(4x \times 5y = 18\).
In 5.3, there are different ways to choose which non-integer variable to branch on. CSIPS branches on the first one or the most infeasible .
There are more sophisticated methods for solving the integer problem, such as branch-and-cut or branch-and-price. Unfortunately, these are difficult to investigate using scipy's linprog, as none of its solver methods make the tableau form accessible.
Exact 2.1.0
pip install Exact Copy PIP instructions
Released: Jun 5, 2024
Python bindings for Exact
Verified details
Maintainers.

Unverified details
Project links.
License: GNU Affero General Public License v3
Author: Jo Devriendt
Requires: Python >=3.10
Classifiers
- OSI Approved :: GNU Affero General Public License v3
- Python :: 3
Project description
Exact solves decision and optimization problems formulated as integer linear programs. Under the hood, it converts integer variables to binary (0-1) variables and applies highly efficient propagation routines and strong cutting-planes / pseudo-Boolean conflict analysis.
Exact is a fork of RoundingSat and improves upon its predecessor in reliability, performance and ease-of-use. In particular, Exact supports integer variables, reified linear constraints, multiplication constraints, and propagation and count inferences. The name "Exact" reflects that the answers are fully sound, as approximate and floating-point calculations only occur in heuristic parts of the algorithm. As such, Exact can soundly be used for verification and theorem proving, where its envisioned ability to emit machine-checkable certificates of optimality and unsatisfiability should prove useful.
- Native conflict analysis over binary linear constraints, constructing full-blown cutting planes proofs.
- Highly efficient watched propagation routines.
- Seamless use of arbitrary precision arithmetic when needed.
- Hybrid linear (top-down) and core-guided (bottom-up) optimization.
- Optional integration with the SoPlex LP solver .
- Core solver also compiles on macOS and Windows .
- Under development: Python interface with assumption solving and reuse of solver state (Linux only for now).
- Under development: generation of certificates of optimality and unsatisfiability that can be automatically verified by VeriPB .
Python interface
Pypi package.
The easiest way is to use Exact's Python interfaces is on an x86_64 machine with Windows or Linux . In that case, install this precompiled PyPi package , e.g., by running pip install exact .
Compile your own Python package
To use the Exact Python interface with optimal binaries for your machine (and the option to include SoPlex in the binary), compile as a shared library and install it with your package manager. E.g., on Linux systems, running pip install . in Exact's root directory should do the trick. On Windows, uncomment the build options below # FOR WINDOWS and comment out those for # FOR LINUX . Make sure to have the Boost libraries installed (see dependencies).
Documentation
The header file Exact.hpp contains the C++ methods exposed to Python via Pybind11 as well as their description. This is probably the best place to start to learn about Exact's Python interface.
Next, python_examples contains instructive examples. Of particular interest is the knapsack tutorial , which is fully commented, starts simple, and ends with some of Exact's advanced features.
Command line usage
Exact takes as command line input an integer linear program and outputs a(n optimal) solution or reports that none exists. Either pipe the program
or pass the file as a parameter
Use the flag --help to display a list of runtime parameters.
Exact supports five input formats (described in more detail in InputFormats.md ):
- .opb pseudo-Boolean decision and optimization (equivalent to 0-1 integer linear programming)
- .wbo weighted pseudo-Boolean optimization (0-1 integer linear programming with weighted soft constraints)
- .cnf DIMACS Conjunctive Normal Form (CNF)
- .wcnf Weighted Conjunctive Normal Form (WCNF)
- .mps Mathematical Programming System (MPS) via the optional CoinUtils library
- .lp Linear Program (LP) via the optional CoinUtils library
Note that .mps and .lp allow rational variables, which are not supported by Exact. Additionally, these formats permit floating point values, which may lead to tricky issues . Rewrite constraints with fractional values to integral ones by multiplying with the lowest common multiple of the denominators.
By default, Exact decides on the format based on the filename extension, but this can be overridden with the --format option.
Compilation from source
In the root directory of Exact:
Replace make by cmake --build . on Windows. For more builds, similar build directories can be created.
For installing system-wide or to the CMAKE_INSTALL_PREFIX root, use make install (on Linux).
Dependencies
- A recent C++20 compiler (GCC, Clang or MSVC should do)
- Boost library, minimal version 1.65. On a Debian/Ubuntu system, install with sudo apt install libboost-dev . On Windows, follow the instructions on boost.org
- Optionally: CoinUtils library to parse MPS and LP file formats. Use CMake option -Dcoinutils=ON after installing the library .
- Optionally: SoPlex LP solver (see below).
SoPlex (on Linux)
Exact supports an integration with the LP solver SoPlex to improve its search routine. For this, checkout SoPlex from its git repository as a submodule, compile it in some separate directory, and configure the right CMake options when compiling Exact.
By default, the following commands in Exact's root directory should work with a freshly checked out repository:
The CMake options soplex_src and soplex_build allow to look for SoPlex in a different location.
Exact is licensed under the AGPLv3 . If this would hinder your intended usage, please contact @JoD.
The current set of benchmarks which is used to assess performance is available here .
If you use Exact, please star and cite this repository and cite the RoundingSat origin paper (which focuses on cutting planes conflict analysis): [EN18] J. Elffers, J. Nordström. Divide and Conquer: Towards Faster Pseudo-Boolean Solving. IJCAI 2018
Please cite any of the following papers if they are relevant.
Integration with SoPlex: [DGN20] J. Devriendt, A. Gleixner, J. Nordström. Learn to Relax: Integrating 0-1 Integer Linear Programming with Pseudo-Boolean Conflict-Driven Search. CPAIOR 2020 / Constraints journal
Watched propagation: [D20] J. Devriendt. Watched Propagation for 0-1 Integer Linear Constraints. CP 2020
Core-guided optimization: [DGDNS21] J. Devriendt, S. Gocht, E. Demirović, J. Nordström, P. J. Stuckey. Cutting to the Core of Pseudo-Boolean Optimization: Combining Core-Guided Search with Cutting Planes Reasoning. AAAI 2021
Project details
Release history release notifications | rss feed.
Jun 5, 2024
Jun 4, 2024
Jul 19, 2023
Jun 26, 2023
Jun 13, 2023
Jun 5, 2023
May 29, 2023
Oct 1, 2022
Apr 20, 2022
Apr 19, 2022
Sep 20, 2021
Aug 24, 2021
Aug 23, 2021
Aug 18, 2021
Aug 17, 2021
Download files
Download the file for your platform. If you're not sure which to choose, learn more about installing packages .
Source Distributions
Built distributions.
Uploaded Jun 5, 2024 CPython 3.12 Windows x86-64
Uploaded Jun 5, 2024 CPython 3.12 manylinux: glibc 2.27+ x86-64 manylinux: glibc 2.28+ x86-64
Uploaded Jun 5, 2024 CPython 3.11 manylinux: glibc 2.27+ x86-64 manylinux: glibc 2.28+ x86-64
Uploaded Jun 5, 2024 CPython 3.10 manylinux: glibc 2.27+ x86-64 manylinux: glibc 2.28+ x86-64
Hashes for Exact-2.1.0-cp312-cp312-win_amd64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | ||
| MD5 | ||
| BLAKE2b-256 |
Hashes for Exact-2.1.0-cp312-cp312-manylinux_2_27_x86_64.manylinux_2_28_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | ||
| MD5 | ||
| BLAKE2b-256 |
Hashes for Exact-2.1.0-cp311-cp311-manylinux_2_27_x86_64.manylinux_2_28_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | ||
| MD5 | ||
| BLAKE2b-256 |
Hashes for Exact-2.1.0-cp310-cp310-manylinux_2_27_x86_64.manylinux_2_28_x86_64.whl
| Algorithm | Hash digest | |
|---|---|---|
| SHA256 | ||
| MD5 | ||
| BLAKE2b-256 |
- português (Brasil)
Supported by

Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Python solvers for mixed-integer nonlinear constrained optimization
I want to minimize a black box function $f(x)$, which takes a 8$\times$3 matrix of non-negative integers as input. Each row specifies a variable, whereas each column specifies a certain time period so that $x_{ij}$ is the $i$th variable in the $j$th time period.
$f(x)$ is the activation function for a convolutional filter in the 2. convolutional layer of a convolutional neural network. It is therefore expected to be nonlinear and nonconvex. The input is subject to constraints as seen below, where $\text{sgn}(x)$ is the sign function as defined at Wikipedia .
\begin{aligned} \text{Objective:} \hspace{1cm} & \text{minimize} \hspace{0.2cm} f(x)\\ \text{Constraints:} \hspace{1cm} & \sum_{i=3}^{6}\sum_{j=1}^{3} x_{ij} = 10 & \\ & x_{3j} + x_{5j} \geq x_{1j} &\forall j = 1,2,3\\ & x_{4j} + x_{6j} \geq x_{2j} &\forall j = 1,2,3\\ & x_{7j} \leq 15 &\forall j = 1,2,3\\ & x_{8j} \leq 15 &\forall j = 1,2,3\\ & \text{sgn}(x_{7j}) = \text{sgn}(x_{3j}) &\forall j = 1,2,3 \\ & \text{sgn}(x_{8j}) = \text{sgn}(x_{4j}) &\forall j = 1,2,3 \\ & x_{ij} \in \mathbb{N_0} &\forall i = 1,2,\cdots,8 \hspace{0.2cm} \forall j = 1,2,3 \end{aligned}
Can anyone recommend any Python packages that would be able to solve this problem? Any commercial software with an interface to Python and a free academic license/evaluation period would also be great.
EDIT: It should be noted that the optimization does not have to find a global minimum (although that is, of course, preferred).
- optimization
- $\begingroup$ I might not have explained the problem well enough (see the updated question). It is nonlinear and I am certain that the optimal solution will have D's unequal to 0. $\endgroup$ – pir Commented Jun 7, 2015 at 8:01
- 2 $\begingroup$ @felbo: I'm guess that your nonlinearity consists of the restrictions on signs of certain pairs of unknowns. If you are asking how to solve this problem with off-the-shelf software packages, one approach would be breaking each of those pair-sign constraints into pairs of inequalities, e.g. $x_{7,j} \gt 0$ and $x_{3,j} \gt 0$ OR $x_{7,j} \lt 0$ and $x_{3,j} \lt 0$ (trusting you to fill in the details about how signs for zero values should be treated). But perhaps you are not as much interested in this one problem as in a broader survey of integer optimization software. $\endgroup$ – hardmath ♦ Commented Jun 7, 2015 at 14:00
- 1 $\begingroup$ @hardmath: I'm not interested in a broader survey of integer optimization software, but in solving this exact problem. Breaking the pair-sign constraints into pairs of inequalities sounds like a great idea if that can be used as input for off-the-shelf packages! The nonlinearity I mentioned in the question is not regarding the constraints, but regarding the function $f(x)$. Do you have any recommendation on off-the-shelf software for black box optimization after your reformulation of the constraints? $\endgroup$ – pir Commented Jun 7, 2015 at 14:12
- 2 $\begingroup$ @felbo: I see. Given the difficult (nonlinear, nonconvex) behavior of your function $f(x)$, I would focus on effciently generating all feasible points $(x_{i,j})$ in your domain and evaluating the function at those points. Off-the-shelf software would not be likely to do anything more intelligent than such exhaustive search. $\endgroup$ – hardmath ♦ Commented Jun 7, 2015 at 14:19
- 1 $\begingroup$ What if I could start the optimization with values $x_0$, where it is known that $f(x_0)$ is close to a local minimum? So it would just have to find closest minimum. Perhaps Ipopt as suggested by @DavidKetcheson would be a good bet? $\endgroup$ – pir Commented Jun 7, 2015 at 15:00
3 Answers 3
I want to minimize a black box function $f(x)$, which takes a 8×3 matrix of non-negative integers as input.
In general, this sort of problem should be solved with a derivative-free MINLP (or if the function is linear, an MILP) solver. A very cursory glance at the literature suggests that the algorithm DFL, presented in a JOTA paper (also see preprint ) could work; there might be other algorithms that also solve derivative-free MINLPs. The authors' implementation is in Fortran 90, so you would need to write some wrappers.
Generally speaking, though, you need some solver that can solve:
- black-box/derivative-free problems (I assume here that derivatives are not available, otherwise it would not be "black box")
- that are also mixed-integer
Since your problem contains no continuous decision variables, exhaustive sampling, as proposed by @hardmath, is another option that is probably easier to implement if you'd rather not write Python wrappers to a Fortran package (I wouldn't blame you).
However, IPOPT would not work, because it requires at least gradient information, and solves continuous problems, not mixed-integer problems. Even ignoring that estimating both gradient and Hessian information with finite-difference-type approaches is likely to yield poor outcomes due to numerical errors in these approximations, IPOPT will only solve the continuous relaxation of the problem. IPOPT (like any other continuous optimization solver) would have to be augmented with branch-and-cut or branch-and-bound-type methods, which is a great deal of work. If you're going to forge ahead and use a solver that assumes you have gradient information (even though you don't), you would be much better served using an MINLP solver (e.g., BARON, Couenne, Bonmin) that would at least give you integer-feasible solutions.
- 1 $\begingroup$ Why is it mixed-integer? All the parameters are integers. $\endgroup$ – pir Commented Jun 18, 2015 at 15:11
- 3 $\begingroup$ Purely integer programs are a subset of mixed-integer programs. Since methods for solving integer programs include approaches like relaxing the integer variables to continuous variables, then solving using a branch-and-bound (or branch-and-cut, or other) scheme, from an implementation perspective, implementing an integer programming solver frequently means mixed-integer programs can also be solved. $\endgroup$ – Geoff Oxberry Commented Jun 18, 2015 at 22:15
- $\begingroup$ Can you recommend an MINLP solver that has an interface to something more accessible than Fortran and C? A solver with a Python interface would be amazing. $\endgroup$ – pir Commented Mar 7, 2016 at 13:45
- 1 $\begingroup$ @pir: I know there are black-box MINLP solvers implemented in MATLAB, but I don't know if they've been released. If you're just looking for MINLP solvers in the standard case where you know your objective and constraints (and these are not black box, plus you can compute derivatives), you might try interfacing to them via modeling languages like GAMS, AMPL, JuMP (Julia), or Pyomo (Python). There should be a MATLAB interface as well, I just don't remember what it is off the top of my head. $\endgroup$ – Geoff Oxberry Commented Mar 7, 2016 at 20:51
- $\begingroup$ Thanks! I am able to compute the first-order derivatives, but the function would still be black box in the sense that it cannot be formulated in a concise mathematical way (output of a neural network). Do you have any recommendations for which solver to use of the ones available in Pyomo? ( software.sandia.gov/downloads/pub/pyomo/… ) $\endgroup$ – pir Commented Mar 7, 2016 at 22:19
I agree with all of the answers provided here but I wanted to supplement with a Python implementation. We developed the Python GEKKO package for solving similar problems. We're also working on machine learning functions that may be able to combine a convolutional neural network with this constrained mixed-integer problem as a single optimization. Here is a potential solution with Python GEKKO (>0.2rc4) .
When you switch to IPOPT with m.options.SOLVER=3 , it gives a non-integer solution, as expected:
However, when you switch to the APOPT MINLP solver with m.options.SOLVER = 1 , it gives an integer solution:
As you can see, the solution is fast but it is likely because the problem size is small and the objective function is not correct. For small problems, an exhaustive search may be the right solution. However, if you scale-up to larger problems with more integer variables or include the convolutional neural network model, each NLP branch and bound sub-problem will take longer to solve or may not converge.
- $\begingroup$ Branch and Bound $\endgroup$ – JeeyCi Commented Oct 20, 2023 at 5:05
- 1 $\begingroup$ still Gekko returns float representation of result.x , thus can convert it to integers with res_milp.x=[int(xi) for xi in res_milp.x] $\endgroup$ – JeeyCi Commented Oct 20, 2023 at 5:07
- 2 $\begingroup$ That is correct. Gekko has an integer tolerance where it can find a solution within 1e-2 of the integer value. This can be adjusted with the solver option minlp_integer_tol . Solutions are always reported as floating point values. Solver options are available here: apmonitor.com/wiki/index.php/Main/OptionApmSolver $\endgroup$ – John Hedengren Commented Oct 20, 2023 at 12:53
The feasible region can be broken up into several "convex" integer lattice subdomains by setting out the specific combinations of sign-agreement pairs. [That is, each sign agreement between $x_{7,j}$ and $x_{3,j}$, resp. between $x_{8,j}$ and $x_{4,j}$ can occur in one of two ways: both positive or both zero. Given the three "time" indices $j=1,2,3$, there are $2^6 = 64$ "components" which are the integer lattice solutions of linear constraints.]
When the region described by linear constraints is too complicated or large for direct generation of all feasible points, a popular technique is to generate a random sample of the points, e.g. by a Monte Carlo Markov Chain (MCMC) algorithm .
There is a Python implementation of MCMC samplers as pymc by Christopher Fonnesbeck, Anand Patil and David Huard. Although targeted to Bayesian estimation, the sampling portion of the toolkit could be used to generate "random" feasible points from each subdomain described above.
The minimum would then be approximated by the least value of $f(x)$ attained over all the sampled points.
Here is a sketch of how one might generate all the feasible points for these particular constraints.
Note that the "odd" row and "even" row indices $i$ are linked only by the sum-to-ten constraint at top. We can rearrange the unknowns from the $8\times 3$ matrix $x$ into a $4\times 6$ matrix:
$$ \begin{pmatrix} x_{1,1} & x_{1,2} & x_{1,3} & x_{2,1} & x_{2,2} & x_{2,3} \\ x_{3,1} & x_{3,2} & x_{3,3} & x_{4,1} & x_{4,2} & x_{4,3} \\ x_{5,1} & x_{5,2} & x_{5,3} & x_{6,1} & x_{6,2} & x_{6,3} \\ x_{7,1} & x_{7,2} & x_{7,3} & x_{8,1} & x_{8,2} & x_{8,3} \end{pmatrix} $$
Each column of non-negative integers $(a,b,c,d)^T$ in this form obeys the same constraints:
$$ a \le b + c $$
$$ {b = 0} \Leftrightarrow {d = 0} $$
$$ d \le 15 $$
We can add the constraint $b+c \le 10$ deduced from the combined middle two row sums in the new form being exactly ten, and we get a finite set of possibilities $S \subset \mathbb{N}_0^4$ from which all six columns are chosen.
Furthermore the sum-to-ten constraint for the two middle rows allows us to assign parts that add to $10$ for the six columns, thereby generating all the feasible points for this problem. There are $35$ partitions of $10$ in not more than six parts, and $\binom{15}{5} = 3003$ weak compositions of $10$ in exactly six summands, so this appears to be a tractable task computationally.
Added: A program written to carry out these calculations found some 8 trillion feasible solutions. More precisely there are 8,054,848,375,116 black box function evaluations needed to exhaust the search space.
- $\begingroup$ Sounds interesting! Note that $ x_{i,j} \in \mathbb{N_0} $ $ \forall i = 1,2,..,8$ $ \forall j = 1,2,3 $, allowing only two ways of sign agreement. Based on my understanding there would then be $ 2^{2 \cdot 3} = 64 $ components. $\endgroup$ – pir Commented Jun 7, 2015 at 19:33
- $\begingroup$ How do you know that each integer lattice subdomain is "convex"? $\endgroup$ – pir Commented Jun 7, 2015 at 19:51
- $\begingroup$ The mention of "convex" was perhaps too terse/cryptic. Any nonempty region of $\mathbb{R}^n$ defined by linear equalities and inequalities is necessarily convex. What I meant by "convex" is the nonmepty intersection of the integer lattice $\mathbb{Z}^n$ with a convex subset of $\mathbb{R}^n$. Unfortunately there seems to be no succinct name for this. Because these sets are disconnected if they contain more than one point, generally these are not truly convex sets (though their theory and the application of MCMC algorithms is tied to convexity). $\endgroup$ – hardmath ♦ Commented Jun 8, 2015 at 0:09
- 1 $\begingroup$ The constraint is not across all $x_{ij}$, but only for $i = 3,\cdots,6$. $\endgroup$ – pir Commented Jun 8, 2015 at 16:24
- 1 $\begingroup$ @hardmath: The terminology I'd use is that the continuous relaxation of the problem is convex. $\endgroup$ – Geoff Oxberry Commented Jun 17, 2015 at 1:07
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged optimization python or ask your own question .
- Featured on Meta
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- We spent a sprint addressing your requests — here’s how it went
Hot Network Questions
- 2024 UK election: Which demographic factors explain the geography?
- Directions of puff pastry folds
- Why was this a draw?
- Did Joe Biden refer to himself as a black woman?
- Can you be charged with breaking and entering if the door was open, and the owner of the property is deceased?
- Would this telescope be capable to detect Middle Ages Civilization?
- How much does a factory reset help in hiding a device's identification details?
- I forgot to remove all authors' names from the appendix for a double-blind journal submission. What are the potential consequences?
- firefox returns odd results for file:/// or file:///tmp
- Why was this a draw? What move I supposed to play to win?
- Weather on a Flat, Infinite Sea
- Capture multiple errors before raising an exception
- How often should I replace my tires on my mountain bike?
- How do I drill a 60cm hole in a tree stump, 4.4 cm wide?
- Everything has a tiny nuclear reactor in it. How much of a concern are illegal nuclear bombs?
- Simulate slow disks in KVM to see effect of LVM cache in test setup
- Why do Electric Aircraft Seem to Eschew Photovoltaics?
- How to solve the intersection truncation problem of multiple \draw[thick, color=xxx] commands by color?
- Has the Supreme Court given any examples where presumptive immunity would be overcome?
- Plastic plugs used to fasten cover over radiator
- Optimizing Pi Estimation Code
- What is the reason for using decibels to measure sound?
- pdfgrep How to locate the pages that contain multiple strings and print the page numbers?
- Any alternative to lockdown browser?

Solving Constraint Integer Programs
How to Cite
- Documentation
Related Work
Team members, cooperation, imprint and privacy statement.
SCIP is currently one of the fastest non-commercial solvers for mixed integer programming (MIP) and mixed integer nonlinear programming (MINLP). It is also a framework for constraint integer programming and branch-cut-and-price. It allows for total control of the solution process and the access of detailed information down to the guts of the solver.
| June/2024 | SCIP version 9.1.0 The SCIP Optimization Suite 9.1.0 (minor release) consists of SCIP 9.1.0, GCG 3.6.2, SoPlex 7.1.0, ZIMPL 3.6.1, PaPILO 2.3.0 and UG 1.0.0 beta 5. Please check the or browse the individual CHANGELOGs of the other projects. |
| May/2024 | SCIP version 9.0.1 The SCIP Optimization Suite 9.0.1 consists of SCIP 9.0.1, GCG 3.6.1, SoPlex 7.0.1, ZIMPL 3.6.0, PaPILO 2.2.1 and UG 1.0.0 beta 4. Please check the or browse the individual CHANGELOGs of the other projects. |
| Feb/2024 | SCIP version 9.0.0 The SCIP Optimization Suite 9.0.0 consists of SCIP 9.0.0, GCG 3.6.0, SoPlex 7.0.0, ZIMPL 3.5.3, PaPILO 2.2.0 and UG 1.0.0 beta 4. Please check the or browse the individual CHANGELOGs of the other projects. |
| Nov/2023 | SCIP version 8.1.0 The SCIP Optimization Suite 8.1.0 consists of SCIP 8.1.0, GCG 3.5.5, SoPlex 6.0.4, ZIMPL 3.5.3, PaPILO 2.1.4 and UG 1.0.0 beta 3. Please check the or browse the individual CHANGELOGs of the other projects. |
| Aug/2023 | SCIP version 8.0.4 The SCIP Optimization Suite 8.0.4 consists of SCIP 8.0.4, GCG 3.5.3, SoPlex 6.0.4, ZIMPL 3.5.3, PaPILO 2.1.3 and UG 1.0.0 beta 3. Please check the or browse the individual CHANGELOGs of the other projects. |
| Dec/2022 | SCIP version 8.0.3 The SCIP Optimization Suite 8.0.3 consists of SCIP 8.0.3, GCG 3.5.3, SoPlex 6.0.3, ZIMPL 3.5.3, PaPILO 2.1.2 and UG 1.0.0 beta 3. Please check the or browse the individual CHANGELOGs of the other projects. |
| 04/Nov/2022 | SCIP license update Starting with the next release SCIP will be licensed under the . |
| 06/Oct/2022 | SCIP version 8.0.2 The SCIP Optimization Suite 8.0.2 consists of SCIP 8.0.2, GCG 3.5.2, SoPlex 6.0.2, ZIMPL 3.5.3, PaPILO 2.1.1 and UG 1.0.0 beta 2. Please check the or browse the individual CHANGELOGs of the other projects. |
| Aug/2022 | Announcing the to the vicenary anniversary of SCIP in fall 2022. |
| Jun/2022 | SCIP version 8.0.1 The SCIP Optimization Suite 8.0.1 consists of SCIP 8.0.1, GCG 3.5.1, SoPlex 6.0.1, ZIMPL 3.5.2, PaPILO 2.1.0 and UG 1.0.0 beta 2. Please check the or browse the individual CHANGELOGs of the other projects. |
| 28/Jan/2022 | SCIP version 8.0.0 The SCIP Optimization Suite 8.0.0 consists of SCIP 8.0.0, GCG 3.5.0, SoPlex 6.0.0, ZIMPL 3.5.1, PaPILO 2.0.0 and UG 1.0.0 beta. Please check the on Optimization Online and the or browse the individual CHANGELOGs of the other projects. |
| 15/Dec/2021 | Beta of SCIP version 8.0.0 released |
| 12/Aug/2021 | SCIP version 7.0.3 The version of the SCIP Optimization Suite 7.0.3 consists of SCIP 7.0.3, GCG 3.0.5, SoPlex 5.0.2, ZIMPL 3.4.0, PaPILO 1.0.2 and UG 0.9.1. It contains bugfixes for SCIP and GCG, see the or browse the individual CHANGELOGs of the other projects. |
| 5/Jun/2021 | Beta of SCIP version 7.0.3 released |
| 26/May/2021 | Public Mirrors on GitHub The two main development branches of , and are now publicly mirrored on GitHub. |
| 13/Jan/2021 | SCIP version 7.0.2 The SCIP Optimization Suite 7.0.2 consists of SCIP 7.0.2, SoPlex 5.0.2, ZIMPL 3.4.0, GCG 3.0.4, PaPILO 1.0.2 and UG 0.9.1. It contains important bugfixes and other improvements for all components of the Optimization Suite, see the or browse the individual CHANGELOGs of the other projects. |
| 19/Dec/2020 | Beta of SCIP version 7.0.2 released |
| 25/Sep/2020 | Patched bliss fork now available on GitHub For symmetry detection the SCIPOptSuite now uses . |
| 23/Jun/2020 | SCIP version 7.0.1 released The SCIP Optimization Suite 7.0.1 consists of SCIP 7.0.1, SoPlex 5.0.1, ZIMPL 3.4.0, GCG 3.0.3, PaPILO 1.0.1 and UG 0.9.0. It contains important bugfixes and other improvements for all components of the Optimization Suite, see the or browse the individual CHANGELOGs of the other projects. |
| 28/May/2020 | Marc Pfetsch and Sebastian Pokutta wrote a blog post about an easy to use . |
| 12/May/2020 | Open positions in the development team: 5 years PostDoc ( ) and 3 years PhD ( )! After the underlying funding scheme of Research Campus MODAL has been extended until 2025, ZIB is looking to grow the SCIP team in different research directions for the next years to come. |
| 20/Apr/2020 | There will be a on 3rd and 4th of June 2020. |
| 8/Apr/2020 | SCIP version 7.0.0 packages updated Source code package and windows executables have been to resolve an error with TBB. |
| 30/Mar/2020 | SCIP version 7.0.0 released The SCIP Optimization Suite 7.0.0 consists of SCIP 7.0.0, SoPlex 5.0.0, ZIMPL 3.3.9, GCG 3.0.3, PaPILO 1.0.0 and UG 0.8.9. It contains important bugfixes and other improvements for all components of the Optimization Suite, see the or browse the individual CHANGELOGs of the other projects. |
| 10/Jul/2019 | SCIP version 6.0.2 released The SCIP Optimization Suite 6.0.2 consists of SCIP 6.0.2, SoPlex 4.0.2, ZIMPL 3.3.8, GCG 3.0.2, and UG 0.8.8. It contains important bugfixes and other improvements for all components of the Optimization Suite, see the or browse the individual CHANGELOGs of the other projects. |
| 28/Jun/2019 | Beta of SCIP version 6.0.2 released |
| 10/Jan/2019 | SCIP version 6.0.1 released The SCIP Optimization Suite 6.0.1 consists of SCIP 6.0.1, SoPlex 4.0.1, ZIMPL 3.3.7, GCG 3.0.1, and UG 0.8.7. It contains important bugfixes and other improvements for all components of the Optimization Suite, see the or browse the individual CHANGELOGs of the other projects. |
| 02/Jul/2018 | SCIP version 6.0.0 released The SCIP Optimization Suite 6.0.0 consists of SCIP 6.0.0, SoPlex 4.0.0, ZIMPL 3.3.6, GCG 3.0.0, and UG 0.8.6. For details regarding the SCIP release, please see the current . An in-depth description of the new features and improvements of all components of the SCIP Optimization Suite can be found in the technical report . |
| 19/Feb/2018 | Visualizing SCIP's branch-and-bound tree Researchers looking for branch-and-bound tree visualizations for SCIP may consider the tool , which has been developed by our colleague Uwe Gotzes. |
older news...
| 05/Feb/2018 | SCIP version 5.0.1 released This is the first bugfix release for version 5 of the SCIP Optimization Suite. A comprehensive list of the fixes and improvements for SCIP can be found in the and the . |
| 21/Dec/2017 | SCIP version 5.0.0 released The SCIP Optimization Suite 5.0.0 consists of SCIP 5.0.0, SoPlex 3.1.0, ZIMPL 3.3.4, GCG 2.1.3, and UG 0.8.5. For more details regarding the SCIP release, please see the current and the . An in-depth description of the new features and improvements of all components of the SCIP Optimization Suite can be found in the technical report . |
| 07/Dec/2017 | We are happy to announce our upcoming from March 6 to 8, 2018 at RWTH Aachen. The workshop provides a forum for current and prospective SCIP users to discuss their applications and share their experience with SCIP. |
| 28/Sep/2017 | SCIP featured in the ScaLP library SCIP is interfaced by . This new, lightweight C++ wrapper library provides a unique interface to several OR solvers and is developed by the digital technology group at the University of Kassel, Germany. |
| 01/Sep/2017 | SCIP version 4.0.1 released The SCIP Optimization Suite 4.0.1 consists of SCIP 4.0.1, SoPlex 3.0.1, ZIMPL 3.3.4, GCG 2.1.2, and UG 0.8.4. For more details regarding the SCIP release, please see the current and the . |
| 09/Mar/2017 | SCIP version 4.0.0 released The SCIP Optimization Suite 4.0.0 consists of SCIP 4.0.0, SoPlex 3.0.0, ZIMPL 3.3.4, GCG 2.1.2, and UG 0.8.3. For more details regarding the SCIP release, please see the current and the . An in-depth description of the new features and improvements of all components of the SCIP Optimization Suite can be found in the technical report . |
| 01/Sep/2016 | The Java interface is also now available on GitHub: . |
| 08/Jul/2016 | The Python interface has been externalized to GitHub for easier collaboration: . We also released a for the SCIP Optimization Suite 3.2.1 necessary to build the updated interface. |
| 25/May/2016 | Release of , the mixed-integer semidefinite programming plugin for SCIP, developed at TU Darmstadt. |
| 29/Feb/2016 | SCIP version 3.2.1 released The SCIP Optimization Suite 3.2.1 consists of SCIP 3.2.1, SoPlex 2.2.1, ZIMPL 3.3.3, GCG 2.1.1, and UG 0.8.2. For more details, please see the current . There is also a about new features and improvements in the SCIP Optimization Suite 3.2. |
| 27/Oct/2015 | uses SCIP for subtasks requiring the solution of Integer Programming problems. Normaliz is a tool for computations in affine monoids, vector configurations, lattice polytopes, and rational cones developed at the University of Osnabrück. |
| 28/Sep/2015 | Workshop/Lecture/Winter School "Combinatorial Optimization @ Work" is held at ZIB! Check out the program (including slides of all presentations). |
| 03/Aug/2015 | – new open-source parallel solver for stochastic mixed-integer programming using SCIP |
| 31/Jul/2015 | is released, replacing UG 0.8.0 of the |
| 01/Jul/2015 | SCIP version 3.2.0 released (see and ). The SCIP Optimization Suite 3.2.0 consists of SCIP 3.2.0, SoPlex 2.2.0, ZIMPL 3.3.3, GCG 2.1.0, and UG 0.8.0. |
| 30/Jun/2015 | New Release of , the mixed integer semidefinite programming plugin for SCIP, developed at TU Darmstadt. |
| 23/Mar/2015 | Windows binaries and libraries available for download. |
| 09/Mar/2015 | Upcoming event: in Berlin (ZIB) - application deadline: 01/Aug/2015 |
| 18/Dec/2014 | SCIP version 3.1.1 released The SCIP Optimization Suite 3.1.1 consists of SCIP 3.1.1, SoPlex 2.0.1, ZIMPL 3.3.2, GCG 2.0.1, and UG 0.7.5. See the for details. |
| 21/Jul/2014 | is now available in version 2.10. OPTimization Interface (OPTI) Toolbox is a free MATLAB toolbox for constructing and solving linear, nonlinear, continuous and discrete optimization problems for Windows users. OPTI Toolbox in its current version comes with SCIP 3.0.2. |
| 16/Jul/2014 | We are happy to announce our upcoming from September 30 to October 2, 2014. The workshop provides a forum for current and prospective SCIP users to discuss their applications and share their experience with SCIP. |
| 16/Mar/2014 | Windows binaries and libraries of SCIP 3.1.0 available for download. |
| 27/Feb/2014 | SCIP version 3.1.0 released (see and ). The SCIP Optimization Suite 3.1.0 consists of SCIP 3.1.0, SoPlex 2.0.0, ZIMPL 3.3.2, GCG 2.0.0, and UG 0.7.3. |
| 25/Feb/2014 | Website relaunched. |
| 16/Oct/2013 | SCIP version 3.0.2 released (bug fix release, see and ). The SCIP Optimization Suite 3.0.2 consists of SCIP 3.0.2, SoPlex 1.7.2, and ZIMPL 3.3.1, GCG 1.1.1, and UG 0.7.2. |
| 17/Apr/2013 | Released beta-version of SCIP which can solve MIP instances exactly over the rational numbers (based on SCIP 3.0.0). Download the source code and get information . |
| 18/Jan/2013 | Recently, Sonja Mars from TU Darmstadt and Lars Schewe from the University of Erlangen-Nürnberg released an . |
| 04/Jan/2013 | SCIP version 3.0.1 released (bug fix release, see and ). The SCIP Optimization Suite 3.0.1 consists of SCIP 3.0.1, SoPlex 1.7.1, and ZIMPL 3.3.1, GCG 1.1.0, and UG 0.7.1. Happy New Year! |
| 31/Oct/2012 | There are some new interfaces to SCIP available: The OPTI project provides a MATLAB interface; on top of this, provides a free modeling language; is a python interface for conic optimization. Thanks to all developers, in particular Jonathan Currie, Johan Löfberg, and Guillaume Sagnol. |
| 18/Aug/2012 | The SCIP workshop 2012 will take place at TU Darmstadt on October 8 and 9: See you there! |
| 01/Aug/2012 | SCIP version 3.0.0 released (see and ). The SCIP Optimization Suite 3.0.0 consists of SCIP 3.0.0, SoPlex 1.7.0, ZIMPL 3.3.0, GCG 1.0.0, and UG 0.7.0. |
| 28/Dec/2011 | SCIP version 2.1.1 released (bug fix release, see and ). The ZIB Optimization Suite 2.1.1 consists of SCIP 2.1.1, SoPlex 1.6.0, and ZIMPL 3.2.0. |
| 31/Oct/2011 | SCIP version 2.1.0 released (see and ). The ZIB Optimization Suite 2.1.0 consists of SCIP 2.1.0, SoPlex 1.6.0, and ZIMPL 3.2.0. |
| 26/Aug/2011 | SCIP version 2.0.2 released (see and ). |
| 04/Jan/2011 | SCIP version 2.0.1 released (see ). The ZIB Optimization Suite 2.0.1 consists of SCIP 2.0.1, SoPlex 1.5.0, and ZIMPL 3.1.0 |
| 12/Nov/2010 | There was a performance issue with the precompiled SCIP 2.0.0 binaries for Windows/PC which were compiled with the compilers cl 15 and Intel 11.1. If you downloaded these binaries before 12/Nov/2010, we recommend to download these binaries again. |
| 30/Sep/2010 | SCIP version 2.0.0 released (see ). The ZIB Optimization Suite 2.0.0 consists of SCIP 2.0.0, SoPlex 1.5.0, and ZIMPL 3.1.0 |
| 12/Jan/2010 | A bug in the Makefiles of the SCIP examples may cause data loss. The SCIP 1.2.0 tarball in the download section has been patched. We strongly recommend to replace your current SCIP installation. If you have a custom Makefile, please ensure, that the target "clean" is changed as described |
| 15/Sep/2009 | SCIP version 1.2.0 released (see ). The ZIB Optimization Suite 1.2.0 consists of SCIP 1.2.0, SoPlex 1.4.2, and ZIMPL 3.0.0 |
| 13/Sep/2009 | Ryan J. O'Neil provides a SCIP-python interface |
| 04/Jul/2009 | The results of the are online. SCIP-Soplex participated in twelve categories and scored first eight times, second three times. SCIP-Clp participated in nine categories and scored first five times, second two times. . |
| 20/Feb/2009 | SoPlex version 1.4.1 and Clp version 1.9.0 have been released. We recommend to upw-150. Some precompiled binaries can be found at the . |
| 30/Sep/2008 | Version 1.1.0 released. |
| 27/Feb/2008 | New SCIP Introduction by Cornelius Schwarz, see . |
| 05/Dec/2007 | Upw-150d LP-interface for Mosek, see the . |
| 11+12/Oct/2007 | SCIP Workshop 2007 (in German). |
| 27/Aug/2007 | Version 1.0 released. |
| 21/Aug/2007 | Web site relaunched. |
| 19/Jul/2007 | Tobias Achterberg finished his PhD thesis, which includes a detailed description of SCIP. You can get it . |
| 14/May/2007 | Tobias Achterberg submitted his PhD thesis. The log files for SCIP 0.90f and SCIP 0.90i of the benchmarks conducted in the thesis are available and . |
| 01/Sep/2006 | SCIP Version 0.90 released. |
| 11/Aug/2006 | Linux binaries linked to CLP 1.03.03 available (contributed by Hans Mittelmann). |
| 11/Jul/2006 | MS Visual C++ project files for SCIP 0.82 contributed by Martin C. Mueller. |
| 15/May/2006 | SCIP Version 0.82 released. |
| 03/Jan/2006 | SCIP Version 0.81 released. |
| 20/Sep/2005 | SCIP Version 0.80 released. |
What is SCIP?
A similar technique is used for solving both Integer Programs and Constraint Programs: the problem is successively divided into smaller subproblems (branching) that are solved recursively.
On the other hand, Integer Programming and Constraint Programming have different strengths: Integer Programming uses LP relaxations and cutting planes to provide strong dual bounds, while Constraint Programming can handle arbitrary (non-linear) constraints and uses propagation to tighten domains of variables.
SCIP is a framework for Constraint Integer Programming oriented towards the needs of mathematical programming experts who want to have total control of the solution process and access detailed information down to the guts of the solver. SCIP can also be used as a pure MIP and MINLP solver or as a framework for branch-cut-and-price.
SCIP is implemented as C callable library and provides C++ wrapper classes for user plugins. It can also be used as a standalone program to solve mixed integer linear and nonlinear programs given in various formats such as MPS, LP, flatzinc, CNF, OPB, WBO, PIP, etc. Furthermore, SCIP can directly read ZIMPL models.
Interfaces and LP solvers usable with SCIP
| Interface | implementing custom plugins | building and solving static models | modifying and iterated solving | querying solution pool | setting parameters |
|---|---|---|---|---|---|
| all | yes | yes | yes | yes | |
| all | yes | yes | yes | yes | |
| all | yes | yes | yes | yes | |
| no | yes | no | no | yes | |
| no | yes | no | yes | yes | |
| no | yes | no | no | yes | |
| no | yes | no | yes | yes | |
| yes | yes | yes | yes | yes |
Detailed list of SCIP's features
- very fast standalone solver for linear programming (LP), mixed integer programming (MIP), and mixed integer nonlinear programming (MINLP)
- framework for branching, cutting plane separation, propagation, pricing, and Benders' decomposition,
- constraint handlers to implement arbitrary constraints,
- variable pricers to dynamically create problem variables,
- domain propagators to apply constraint independent propagations on the variables' domains,
- separators for cutting planes based on the LP relaxation; benefit from a dynamic cut pool management,
- relaxators can be included to provide relaxations (e.g., semidefinite relaxations or Lagrangian relaxations) and dual bounds in addition to the LP relaxation, working in parallel or interleaved
- plugins to apply Benders' decomposition and implement Benders' cuts,
- primal heuristics to search for feasible solutions with specific support for probing and diving,
- node selectors to guide the search,
- branching rules to split the problem into subproblems; arbitrarily many children per node can be created, and the different children can be arbitrarily defined,
- presolvers to simplify the solved problem,
- file readers to parse different input file formats,
- event handlers to be informed on specific events, e.g., after a node was solved, a specific variable changes its bounds, or a new primal solution is found,
- display handlers to create additional columns in the solver's output.
- dialog handlers to extend the included command shell.
- conflict analysis can be applied to learn from infeasible subproblems
- dynamic memory management to reduce the number of operation system calls with automatic memory leakage detection in debug mode
What is the SCIP Optimization Suite?
The SCIP Optimization Suite is a toolbox for generating and solving mixed integer nonlinear programs, in particular mixed integer linear programs, and constraint integer programs. It consists of the following parts:
| mixed integer (linear and nonlinear) programming solver and constraint programming framework | |
| linear programming solver | |
| parallel presolve for integer and linear optimization | |
| mathematical programming language | |
| parallel framework for mixed integer (linear and nonlinear) programs | |
| generic branch-cut-and-price solver |
The user can easily generate linear, mixed integer and mixed integer quadratically constrained programs with the modeling language ZIMPL. The resulting model can directly be loaded into SCIP and solved. In the solution process SCIP may use SoPlex as underlying LP solver.
Since all six components are available in source code and free for academic use, they are an ideal tool for academic research purposes and for teaching mixed integer programming.
Download the SCIP Optimization Suite below .
A further extension of SCIP in order to solve MISDPs (mixed-integer semidefinite programs) is available from TU Darmstadt: SCIP-SDP .
The SCIP Optimization Suite 9.0 Suresh Bolusani, Mathieu Besançon, Ksenia Bestuzheva, Antonia Chmiela, João Dionísio, Tim Donkiewicz, Jasper van Doornmalen, Leon Eifler, Mohammed Ghannam, Ambros Gleixner, Christoph Graczyk, Katrin Halbig, Ivo Hedtke, Alexander Hoen, Christopher Hojny, Rolf van der Hulst, Dominik Kamp, Thorsten Koch, Kevin Kofler, Jurgen Lentz, Julian Manns, Gioni Mexi, Erik Mühmer, Marc E. Pfetsch, Franziska Schlösser, Felipe Serrano, Yuji Shinano, Mark Turner, Stefan Vigerske, Dieter Weninger, Lixing Xu Available at Optimization Online and as ZIB-Report 24-02-29 , February 2024 BibTeX
Enabling Research through the SCIP Optimization Suite 8.0 Ksenia Bestuzheva, Mathieu Besançon, Wei-Kun Chen, Antonia Chmiela, Tim Donkiewicz, Jasper van Doornmalen, Leon Eifler, Oliver Gaul, Gerald Gamrath, Ambros Gleixner, Leona Gottwald, Christoph Graczyk, Katrin Halbig, Alexander Hoen, Christopher Hojny, Rolf van der Hulst, Thorsten Koch, Marco Lübbecke, Stephen J. Maher, Frederic Matter, Erik Mühmer, Benjamin Müller, Marc E. Pfetsch, Daniel Rehfeldt, Steffan Schlein, Franziska Schlösser, Felipe Serrano, Yuji Shinano, Boro Sofranac, Mark Turner, Stefan Vigerske, Fabian Wegscheider, Philipp Wellner, Dieter Weninger, Jakob Witzig Available at ACM Digital Library , June 2023 BibTeX
The SCIP Optimization Suite 8.0 Ksenia Bestuzheva, Mathieu Besançon, Wei-Kun Chen, Antonia Chmiela, Tim Donkiewicz, Jasper van Doornmalen, Leon Eifler, Oliver Gaul, Gerald Gamrath, Ambros Gleixner, Leona Gottwald, Christoph Graczyk, Katrin Halbig, Alexander Hoen, Christopher Hojny, Rolf van der Hulst, Thorsten Koch, Marco Lübbecke, Stephen J. Maher, Frederic Matter, Erik Mühmer, Benjamin Müller, Marc E. Pfetsch, Daniel Rehfeldt, Steffan Schlein, Franziska Schlösser, Felipe Serrano, Yuji Shinano, Boro Sofranac, Mark Turner, Stefan Vigerske, Fabian Wegscheider, Philipp Wellner, Dieter Weninger, Jakob Witzig Available at Optimization Online and as ZIB-Report 21-41 , December 2021 BibTeX
The SCIP Optimization Suite 7.0 Gerald Gamrath, Daniel Anderson, Ksenia Bestuzheva, Wei-Kun Chen, Leon Eifler, Maxime Gasse, Patrick Gemander, Ambros Gleixner, Leona Gottwald, Katrin Halbig, Gregor Hendel, Christopher Hojny, Thorsten Koch, Pierre Le Bodic, Stephen J. Maher, Frederic Matter, Matthias Miltenberger, Erik Mühmer, Benjamin Müller, Marc Pfetsch, Franziska Schlösser, Felipe Serrano, Yuji Shinano, Christine Tawfik, Stefan Vigerske, Fabian Wegscheider, Dieter Weninger, Jakob Witzig Available at Optimization Online and as ZIB-Report 20-10 , March 2020 BibTeX
The SCIP Optimization Suite 6.0 Ambros Gleixner, Michael Bastubbe, Leon Eifler, Tristan Gally, Gerald Gamrath, Robert Lion Gottwald, Gregor Hendel, Christopher Hojny, Thorsten Koch, Marco E. Lübbecke, Stephen J. Maher, Matthias Miltenberger, Benjamin Müller, Marc E. Pfetsch, Christian Puchert, Daniel Rehfeldt, Franziska Schlösser, Christoph Schubert, Felipe Serrano, Yuji Shinano, Jan Merlin Viernickel, Matthias Walter, Fabian Wegscheider, Jonas T. Witt, Jakob Witzig Available at Optimization Online and as ZIB-Report 18-26 , July 2018 BibTeX
The SCIP Optimization Suite 5.0 Ambros Gleixner, Leon Eifler, Tristan Gally, Gerald Gamrath, Patrick Gemander, Robert Lion Gottwald, Gregor Hendel, Christopher Hojny, Thorsten Koch, Matthias Miltenberger, Benjamin Müller, Marc E. Pfetsch, Christian Puchert, Daniel Rehfeldt, Franziska Schlösser, Felipe Serrano, Yuji Shinano, Jan Merlin Viernickel, Stefan Vigerske, Dieter Weninger, Jonas T. Witt, Jakob Witzig Available at Optimization Online and as ZIB-Report 17-61 , December 2017 BibTeX
The SCIP Optimization Suite 4.0 Stephen J. Maher, Tobias Fischer, Tristan Gally, Gerald Gamrath, Ambros Gleixner, Robert Lion Gottwald, Gregor Hendel, Thorsten Koch, Marco E. Lübbecke, Matthias Miltenberger, Benjamin Müller, Marc E. Pfetsch, Christian Puchert, Daniel Rehfeldt, Sebastian Schenker, Robert Schwarz, Felipe Serrano, Yuji Shinano, Dieter Weninger, Jonas T. Witt, Jakob Witzig Available at Optimization Online and as ZIB-Report 17-12 , March 2017 BibTeX
The SCIP Optimization Suite 3.2 Gerald Gamrath, Tobias Fischer, Tristan Gally, Ambros M. Gleixner, Gregor Hendel, Thorsten Koch, Stephen J. Maher, Matthias Miltenberger, Benjamin Müller, Marc E. Pfetsch, Christian Puchert, Daniel Rehfeldt, Sebastian Schenker, Robert Schwarz, Felipe Serrano, Yuji Shinano, Stefan Vigerske, Dieter Weninger, Michael Winkler, Jonas T. Witt, Jakob Witzig Available at Optimization Online and as ZIB-Report 15-60 , February 2016 BibTeX
In order to reference the general algorithmic design behind constraint integer programming and SCIP's solving techniques regarding mixed-integer linear and nonlinear programming, please cite the following articles:
- Constraint Integer Programming: a New Approach to Integrate CP and MIP Tobias Achterberg, Timo Berthold, Thorsten Koch, Kati Wolter Integration of AI and OR Techniques in Constraint Programming for Combinatorial Optimization Problems, CPAIOR 2008, LNCS 5015, Pages 6–20, 2008 Available as ZIB Report 08-01 and at SpringerLink , January 2008 BibTeX
- SCIP: Solving Constraint Integer Programs Tobias Achterberg Mathematical Programming Computation, Volume 1, Number 1, Pages 1–41, 2009. Available at Mathematical Programming Computation , 2009 BibTeX
A more detailed description of SCIP can be found in
- Constraint Integer Programming Tobias Achterberg Ph.D. thesis, TU Berlin, July 2007. Available as Doctoral Thesis , January 2009 BibTeX
The features for the global optimization of convex and nonconvex MINLPs are described in
- Global Optimization of Mixed-Integer Nonlinear Programs with SCIP 8 Ksenia Bestuzheva, Antonia Chmiela, Benjamin Müller, Felipe Serrano, Stefan Vigerske, Fabian Wegscheider arXiv:2301.00587, 2023. BibTeX
The extension of SCIP to solve MIPs exactly over rational input data is described in
- A Computational Status Update for Exact Rational Mixed Integer Programming Leon Eifler, Ambros Gleixner Integer Programming and Combinatorial Optimization. IPCO 2021, Lecture Notes in Computer Science, vol 12707. pp. 163-177 BibTeX
However, for the latest developments, please consult our series of release reports .
Since November 4, SCIP is licensed under the Apache 2.0 License .
Releases up to and including Version 8.0.2 remain under the ZIB Academic License as indicated by the files contained in the releases. The new license applies from Version 8.0.3 onwards.
The files you can download here come without warranty . Use at your own risk!
Please note that version x.x.x is currently in beta stage.
Source Code
You can either download SCIP alone or the SCIP Optimization Suite (recommended), a complete source code bundle of SCIP, SoPlex, ZIMPL, GCG, PaPILO and UG.
Click here for information on different platforms ...
- For compilation instructions please consult the installations section of the online documentation.
- SCIP is completely implemented in C. The code should compile with any C compiler that supports the C99 standard. We have tested SCIP with GNU, Clang and Intel compilers on 32- and 64-bit versions of Linux, Mac and Windows.
- If you are using the GNU compiler on SunOS and you experience a strange behavior of your program (segmentation faults), you might try a reduce the optimization level -O2 . If problems occur with STL code, you might change to a different implementation by adding -library=stlport4 to CXX_COMPILER_FLAGS . (Note: There are different implementations of the STL on SUN platforms.)
Precompiled Packages
You can also download precompiled executables of SCIP with which you can solve MIP, MINLP, CIP, SAT, or PBO instances in various formats . Note that these executables do not include the readline features (i.e., command line editing and history) due to license issues. However, you can download the free readline wrapper rlwrap to provide this missing feature to the executables.
If you use conda , you can install the components of the scipoptsuite using the conda packages .
- In order to build SCIP yourself with support for symmetry handling , you need bliss . A patched bliss fork is now available on GitHub . This fork allows to limit the number of search nodes and generators during the backtrack search and improves performance of symmetry handling in SCIP.
- For some of the mac packages you need the libgfortran and libtbb libraries, and bison . You can install them for example via homebrew: `brew install bison`, `brew install gcc` and `brew install tbb` before installing the scipoptsuite. After installation of the .sh package to a custom directory you may need to include the lib folder into your DYLD_LIBRARY_PATH. If you want to compile the Suite on a apple silicon M series processor you might need to set `ARCH=arm` as an argument to make.
- The linux precompiled binaries are built on debian and ubuntu, both debian based distributions. Chances are that you won't be able to install them on a different one, like arch-linux.
- If you download an executable containing PaPILO you might need a working installation of the TBB library in your machine. (This might also be available via your package manager, for debian, for example, it is called `libtbb2`.)
- For GCG on a linux system you need a working installation of hMETIS version >= 2.0, and zsh (apt install zsh) in your system.
- Here is the download section of MIPLIB 2017 benchmark MPS files.
- SCIP is also available on the NEOS Server , where you can post your model in LP or MPS format, or as an AMPL, GAMS, or ZIMPL model and let the NEOS Server solve it with SCIP linked to CPLEX.
- A development version of SCIP 7 to solve MIPs exactly without floating-point roundoff errors is available as a separate download on Github .
- An up-to-date list of publications about SCIP can be found at swMath.org .
Projects at ZIB that use SCIP
- Optimization of Gas Transport ,DFG Research Center Matheon , Project B20.
- Advanced Solver Technology for SCM
- DESI – Durchgängig energiesensible IKT-Produktion
- Exact Integer Programming , DFG Priority Program 1307 Algorithm Engineering .
- Integrated Planning of Multi-layer Networks , DFG Research Center Matheon , Project B3.
- Service Design in Public Transport , DFG Research Center Matheon , Project B15.
- ForNe: Research Cooperation Network Optimization
- Chip Design Verification , DFG Research Center Matheon , Project D17.
- Discrete Morse Functions .
- Infeasible Linear Inequality Systems .
- MLTN - Multi-layer Transport Networks
- Stable sets and special graph classes
- Symmetries in Integer Programming , DFG Research Center Matheon , Project B12.
- VeriCount - Counting Solutions in the Field of Verification
- Scheduling the SBB Cargo Railroad routing and shipment operations at night, Combinatorial Optimization & Graph Algorithms Group , TU Berlin.
- Scheduling Techniques in Constraint Integer Programming, DFG Research Center Matheon , Project B25.

Projects using SCIP (outside ZIB)
- Project A9: Resilient Design from SFB 805: Control of Uncertainties in Load-Carrying Structures in Mechanical Engineering , TU Darmstadt
- Projekt EXPRESS: Exploiting Structure in Compressed Sensing Using Side Constraints from SPP 1798: Compressed Sensing in Information Processing (CoSIP) , TU Darmstadt
- Project A01: Global Methods for Stationary Gastransport from Transregio/SFB 154: Mathematical Modelling, Simulation and Optimization on the Example of Gas Networks , TU Darmstadt
- Project A4: Mathematical Models and Methods for an Optimum Combination of Passive and Active Components from SFB 805: Control of Uncertainties in Load-Carrying Structures in Mechanical Engineering , TU Darmstadt
- DSP – Parallel Solver for Stochastic Mixed-integer Programming Problems, Argonne National Laboratory
- GOBNILP – Globally Optimal Bayesian Network learning using Integer Linear Programming, The University of York
- SCIL – Symbolic Constraints in Integer Linear programming , Max-Planck-Institut für Informatik
- Generic Column Generation , RWTH Aachen
- Normaliz , a tool for computations in affine monoids, vector configurations, lattice polytopes, and rational cones developed at the University of Osnabrück.
- Numberjack – A python constraint programming platform, University College Cork
- Thermos Map-driven web-based software for optimising the layout of heat networks, and associated applications, Centre for Sustainable Energy, UK
Some Papers that use SCIP
- Conflict Analysis in Mixed Integer Programming Tobias Achterberg Discrete Optimization, Special Issue 4, 2007
- Hybrid Branching Tobias Achterberg, Timo Berthold Proc. of CPAIOR 2009, LNCS 5547, 05.2009.
- Improving the Feasibility Pump Tobias Achterberg, Timo Berthold Discrete Optimization, Special Issue 4, 2007
- Constraint Integer Programming: Techniques and Applications Tobias Achterberg, Timo Berthold, Stefan Heinz, Thorsten Koch, Kati Wolter ZIB-Report 08-43.
- Constraint Integer Programming: a New Approach to Integrate CP and MIP Tobias Achterberg, Timo Berthold, Thorsten Koch, Kati Wolter Proc. of CPAIOR 2008, LNCS 5015, 2008
- Teaching MIP Modeling and Solving Tobias Achterberg, Thorsten Koch, and Martin Grötschel ORMS Today 33, no. 6
- Counting solutions of integer programs using unrestricted subtree detection Tobias Achterberg, Stefan Heinz, Thorsten Koch Proc. of CPAIOR 2008, LNCS 5015, 2008
- Experiments with Linear and Semidefinite Relaxations for Solving the Minimum Graph Bisection Problem Michael Armbruster, Marzena Fügenschuh, Christoph Helmberg, and Alexander Martin Technical Report, TU Darmstadt, 2006
- Constrained Clustering using Column Generation Babaki, B., Guns, T., Nijssen, S. CPAIOR, May 2014, Cork, Ireland
- Heuristics of the Branch-Cut-and-Price-Framework SCIP Timo Berthold Operations Research Proceedings 2007
- RENS - Relaxation Enforced Neighborhood Search Timo Berthold ZIB-Report 07-28
- Rapid learning for binary programs Timo Berthold, Thibaut Feydy, Peter J. Stuckey Proc. of CPAIOR 2010, LNCS 6140
- SCIP Optimization Suite を利用した 混合整数(線形/非線形) 計画問題の解法 Timo Berthold, Ambros Gleixner, Stefan Heinz, Thorsten Koch, and Yuji Shinano. ZIB-Report 12-24
- Undercover – a primal heuristic for MINLP based on sub-MIPs generated by set covering Timo Berthold, Ambros M. Gleixner ZIB-Report 09-40
- A Constraint Integer Programming Approach for Resource-Constrained Project Scheduling Timo Berthold, Stefan Heinz, Marco Lübbecke, Rolf H. Möhring, Jens Schulz Proc. of CPAIOR 2010, LNCS 6140
- Nonlinear pseudo-Boolean optimization: relaxation or propagation? Timo Berthold, Stefan Heinz, Marc E. Pfetsch Theory and Applications of Satisfiability Testing – SAT 2009, LNCS 5584, 2009
- Solving Pseudo-Boolean Problems with SCIP Timo Berthold, Stefan Heinz, Marc E. Pfetsch ZIB-Report 08-12
- Extending a CIP framework to solve MIQCPs Timo Berthold, Stefan Heinz, Stefan Vigerske ZIB-Report 09-23
- Comparing MIQCP solvers to a specialised algorithm for mine production scheduling Andreas Bley, Ambros M. Gleixner, Thorsten Koch, Stefan Vigerske ZIB-Report 09-32
- Auslegung heterogener Kommunikationsnetze nach Performance und Wirtschaftlichkeit Andreas Bley, Friederich Kupzog, and Adrian Zymolka Proc. of the 11th Kasseler Symposium Energie-Systemtechnik: Energie und Kommunikation, 2006
- Angebotsplanung im öffentlichen Nahverkehr Ralf Borndörfer, Marika Neumann, Marc E. Pfetsch ZIB-Report 08-04, to appear in Heureka'08
- The Location-Dispatching Problem: polyhedral results and Content Delivery Network Design Philippe Chrétienne, Pierre Fouilhoux, Eric Gourdin, and Jean-Mathieu Segura Electronic Notes in Discrete Mathematics 26, 867-874, 2010
- Coordination of Cluster Ensembles via Exact Methods Ioannis T. Christou IEEE Transactions on Pattern Analysis and Machine Intelligence, 33(2):279—293, 2011
- A Branch-and-Price Algorithm for Multi-mode Resource Leveling Eamonn T. Coughlan, Marco E. Lübbecke and Jens Schulz Proc. of SEA 2010, LNCS 6049, 226-238, 2010
- Models and Algorithms for Maximum Flow Problems Having Semicontinuous Path Flow Constraints Robert Curry and J. Cole Smith IISE Transactions, 2017
- Optimal control of spatial-dynamic processes: the case of biological invasions Rebecca S. Epanchin-Niell and James E. Wilen Agricultural and Applied Economics Association 2010 Annual Meeting
- Integer linear programming models for topology optimization in sheet metal design Armin Fügenschuh and Marzena Fügenschuh Mathematical Methods of Operations Research, to appear (2008)
- Scenario Technique with Integer Programming for Sustainability in Manufacturing Armin Fügenschuh, Pia Gausemeier, Günther Seliger, and Semih Severengiz Lecture Notes in Business Information Processing 46, 320-331, 2010
- Experiments with a Generic Dantzig-Wolfe Decomposition for Integer Programs Gerald Gamrath and Marco E. Lübbecke Proc. of SEA 2010, LNCS 6049, 239-252, 2010
- Ein neuer Ansatz zur Optimierung des Bilanzausgleichs in einem Gasmarktgebiet Uwe Gotzes Zeitschrift für Energiewirtschaft, 1-13, 2019
- Using Model Counting to Find Optimal Distinguishing Tests Stefan Heinz and Martin Sachenbacher Proc. of CPAIOR 2009, LNCS 5547
- Exact and Approximate Sparse Solutions of Underdetermined Linear Equations Sadegh Jokar, Marc E. Pfetsch ZIB-Report 07-05
- Computing Optimal Morse Matchings Michael Joswig and Marc E. Pfetsch SIAM Journal on Discrete Mathematics 20, no. 1, 2006
- Orbitopal Fixing Volker Kaibel, Matthias Peinhardt, and Marc E. Pfetsch Proc. of the 12th Integer Programming and Combinatorial Optimization conference (IPCO) M. Fischetti and D. Williamson (eds.), LNCS 4513, Springer-Verlag, 74-88, 2007
- On connectivity limits in ad hoc networks with beamforming antennas Moritz Kiese, Christian Hartmann, Julian Lamberty, and Robert Vilzmann EURASIP Journal on Wireless Communications and Networking 2009, No.7, 74-88, 02.2009
- Approximated segmentation considering technical and dosimetric constraints in intensity-modulated radiation therapy with electrons Antje Kiesel and Tobias Gauer ArXiv e-prints, May 2010
- Rapid Mathematical Programming or How to Solve Sudoku Puzzles in a few Seconds Thorsten Koch Operations Research Proceedings 2005
- Algorithms to separate {0,1/2}-Chvatal-Gomory cuts Arie M. C. A. Koster, Adrian Zymolka and Manuel Kutschka Algorithmica 55, No. 2, 375-391
- A formulation space search heuristic for packing unequal circles in a fixed size circular container C. O. López and J. E. Beasley European Journal of Operational Research 251 (2016) 64–73
- Large-scale identification of genetic design strategies using local search Desmond S. Lun, Graham Rockwell, Nicholas J. Guido, Michael Baym, Jonathan A. Kelner, Bonnie Berger, James E. Galagan, and George M. Church Molecular Systems Biology 5, No. 296, 2009
- Optimization Methods For Selecting Founder Individuals For Captive Breeding or reintroduction of Endangered Species Webb Miller, Stephen J. Wright, Yu Zhang, Stephan C. Schuster, Vanessa M. Hayes Pacific Symposium on Biocomputing, 43-53, 2010
- Two-layer Network Design by Branch-and-Cut featuring MIP-based Heuristics Sebastian Orlowski, Arie M. C. A. Koster, Christian Raack, and Roland Wessäly Proceedings of the Third International Network Optimization Conference, 2007
- Branch-And-Cut for the Maximum Feasible Subsystem Problem Marc E. Pfetsch SIAM Journal on Optimization 19, No. 1, 21-38 (2008)
- Integer Programming and Sports Rankings Christian Raack, Annie Raymond, Thomas Schlechte, Axel Werner ZIB-Report 13-19
- Rostering from staffing levels: a branch-and-price approach Egbert van der Veen and Bart Veltman Proc. of the 35th International Conference on Operational Research Applied to Health Services, 1-10, 2009
- Faster MIP solutions via new node selection rules Daniel T. Wojtaszeka and John W. Chinneck Computers & Operations Research 37, 1544-1556, September 2009
- Optimal Packings of Congruent Circles on a Square Flat Torus as Mixed-Integer Nonlinear Optimization Problem. Vladimir Voloshinov and Sergey Smirnov Voevodin V., Sobolev S. (eds) Supercomputing. RuSCDays 2019. Communications in Computer and Information Science, vol 1129. Springer, December 2019
- Robust Aircraft Routing Chiwei Yan and Jerry Kung INFORMS Transportation Science, July 2016
If you know about further projects or papers that use SCIP, please let us know .
For general information or questions about SCIP please write to the SCIP mailing list [email protected] after subscribing to it at the SCIP mailing list page . For licensing questions, please see the license section of the web page and the contact provided there. Trouble compiling SCIP from source? Please check the build documentation before sending an email. For questions about our SCIP interfaces on GitHub please open an issue in the corresponding repository.
Mailing List
The SCIP mailing list can be accessed via the SCIP mailing list page . You can conveniently search the archives using Google: site:listserv.zib.de/pipermail/scip
Stack Overflow
We are also watching the SCIP tag on stackoverflow.com and will answer your questions there. Note that we will not answer faster only because you posted the same question both to stack overflow and the mailing list.
Reporting Bugs
SCIP has more than 500,000 lines of source code and is definitely not bug free. If you'd like to help us improve SCIP, visit our bug submission page and file a bug report in English or German.
| Project Head | |
| Head of development | |
| Mixed-integer linear and non-linear formulations | |
| Cutting planes | |
| Machine learning for optimization, cutting planes | |
| Symmetry handling | |
| Verification, exact MIP | |
| Rust interface | |
| General framework, exact SCIP & SoPlex, verification | |
| Machine learning for optimization | |
| Mixed-integer programming, decomposition heuristics | |
| Presolving | |
| Symmetry handling | |
| Network optimization, total unimodularity | |
| Robustness | |
| Algebraic Modeling Language ZIMPL | |
| Decomposition framework GCG | |
| Shared memory parallelization, Benders decomposition | |
| Test and release management | |
| Primal heuristics, conflict analysis | |
| LP solvers, special math programming constraints, symmetry handling | |
| Parallelization framework UG | |
| Cutting planes selection and branching | |
| Mixed integer nonlinear programming | |
| Multilinear optimization | |
| Presolving, mixed integer programming, decomposition methods | |
| Mixed-integer nonlinear programming |
| Creator and first developer of SCIP | |
| Primal heuristics, branching rules | |
| Tobias Fischer | Constraint handler for special ordered sets, type one; cardinality constraint handler |
| Tristan Gally | Relaxation Handlers, SCIP-SDP |
| Column generation, mixed integer programming, branching | |
| Shared memory parallelization, cutting planes, presolving, CMake | |
| Solution counting, global constraints, conflict analysis | |
| Primal heuristics, mixed integer programming, solver intelligence, CMake, SCIP documentation | |
| Developer of SIP – the predecessor of SCIP | |
| LP interfaces, Python interface, CMake | |
| Mixed integer nonlinear programming, domain propagation | |
| Test management | |
| Nonlinear programming, cutting planes, Python interface | |
| Parallelization, conflict analysis | |
| Fabian Wegscheider | Symmetries in mixed integer nonlinear programming |
| Presolving, pseudo boolean constraint handler | |
| Reoptimization, conflict analysis, mixed integer programming | |
| Kati Jarck | Cutting planes, exact integer programming |
Student Assistants
| Matea Miskovic | Primal heuristics |
Click here for a list of further contributors ...
We are thankful to many people who over the years have contributed code to SCIP, among others:
| Daniel Anderson | Treemodel scoring rules, treesize estimation |
| Martin Ballerstein | Constraint Handler for bivariate nonlinear constraints |
| Logic-based Bender's decomposition | |
| Livio Bertacco | Interface to |
| VRP example | |
| Pierre Le Bodic | Treemodel scoring rules, treesize estimation |
| Tobias Buchwald | Dual value heuristic |
| Weikun Chen | Dual sparsify presolver |
| Frederic Didier | Glop LP interface |
| Interface to | |
| John Forrest | Interface to |
| Fabian Frickenstein | Verification |
| Maxime Gasse | Vanilla full strong branching |
| Thorsten Gellermann | Generic NLP interface |
| Patrick Gemander | Presolving, mixed integer programming |
| Sudoku example | |
| Bo Jensen | Interface to |
| Interface to | |
| Separator for {0,1/2}-cuts | |
| Anna Melchiori | Multi-aggregated variable branching rule |
| Dennis Michaels | Constraint Handler for bivariate nonlinear constraints |
| GMI example | |
| Michael Perregaard | Interface to |
| Frédéric Pythoud | Superindicator constraint handler |
| Christian Raack | Separator for MCF cuts |
| Branch-and-Price contributions | |
| Steiner Tree Problem application | |
| Feasibility Pump 2.0 | |
| Sebastian Schenker | PolySCIP |
| Scheduling plugins: cumulative and linking constraint handler, variable bounds propagator | |
| Cornelius Schwarz | Queens example |
| Robert Schwarz | Python interface |
| JNI interface | |
| Parallel extension of SCIP | |
| Exact integer programming | |
| Timo Strunk | PolySCIP |
| Andreas Tuchscherer | Branch-and-Price contributions |
| Ingmar Vierhaus | Nonlinear constraint parsing in CIP reader |
| OBBT propagator |
SCIP is developed in cooperation with

© 2024 by Zuse Institute Berlin (ZIB). For the imprint and privacy statement we refer to the Imprint of ZIB with the following additions and modifications:
Download form
The number of SCIP downloads is tracked and used to generate statistics about the downloads and to generate the world map of download locations. The personal information is used to distinguish the number of downloads from the number of users per year that might download more than one version or archive. In addition to the privacy statements of ZIB, we hereby declare that your name and affiliation recorded for the SCIP download is used for purposes of granting licenses and for statistics about software downloads, and is processed and stored on our server for the duration of a year.
themodernscientist
Data scientist, biophysicist, mac-unix zealot, pythonista, binary integer programming with python.
My research is focused on biomolecular NMR and, as such, often involves transferring resonance assignments from one multidimensional NMR spectrum to another. In theory this should be a simple task, but it can be extremely time consuming due to small variations in the sample used to acquire the data or in the way the data were acquired.
The good news, however, is that it is possible to automate this process using an optimization. Optimization problems, such as aligning x-ray crystallographic models of homologous proteins, are often encountered in structural biology. In the case of a structural alignment, the transformed structure can occupy any set of coordinates, provided the shape of the molecule itself is not changed. The transfer of resonance assignments is different in that individual resonances are either matched with each other or not. The transformation from one set of data onto another is effectively discrete (more specifically, it is binary). This type of optimization is known as “binary integer programming.”
When I attempted to write a script to perform this type of optimization using python, I found some excellent background reading but very little information on how to implement such a calculation. Being someone who learns by example, I thought it would be useful to share how I setup a simple binary integer programming calculation using two different python libraries 2 that interact with open source solvers written in ANSI C. 1
This notebook demonstrates how to use python to interface with two open source packages for binary integer programming, GLPK and lp_solve . These packages are demonstrated using two python libraries, CVXOPT , which interacts with GLPK, and lp_solve's own python interface. An example for matching five x,y -coordinate pairs from two different data sets is shown for each library.
Setup notes and module import ¶
CVXOPT must be installed with GLPK support and lp_solve with python bindings must be installed. GLPK, lp_solve (without python interface), and CVXOPT are available via MacPorts . I have created a GitHub repository with the MacPorts configuration files necessary to install lp_solve with its python bindings. Alternatively, the python functionality for lp_solve could be installed in a separate repository with virtualenv . The import statements below assume that GLPK and CVXOPT have been installed as provided by MacPorts and the modified lp_solve from GitHub has been installed within MacPorts as well. Finally, numpy is required for working with arrays. Matplotlib is required only if plotting the results of the optimization is desired.
Create two data sets ¶
The first data set contains five x,y -coordinate pairs where the first column is x - and the second column is y -data.
The second data set is similar to the first but has random noise added to it. The order of the points is also shuffled so the optimization solution isn't trivial.
Add some names for the data points and shuffle them in the same way for the second data set. This will be useful later when determining if the peaks were correctly matched.
Calculate the distance between each pair of data points ¶
The goal of the optimization is to minimize the sum of the distance between each set of matched points. Thus, the cartesian distance must be calculated for each point in data1 and the set of points in data2 . The simplest way to do this is with a distance matrix containing all peaks from data1 along one axis and those from data2 along the second axis.
In the above line, n_data1 and n_data2 are the number of points in data1 and data2 , respectively.
Setup the binary integer programming problem ¶
In addition to calculating the distance matrix, the optimization requires setting constraints to ensure that each point in one data set is paired with at most one point in the corresponding data set. This is accomplished using the following two constraints:
$\matrix{A} \space \times \space \matrix{X} \space = \space \matrix{b}$
$\matrix{C} \space \times \space \matrix{X} \space \leq \space \matrix{d}$
where $\matrix{A}$ and $\matrix{C}$ are binary (all values are either 0 or 1 ) matrices whose first dimensions are n_data1 and n_data2 , respectively, and both second dimensions are the product of the two data set sizes, n_data1 $\times$ n_data2 . $\matrix{b}$ and $\matrix{d}$ are column vectors of length n_data1 and n_data2 , respectively, whose value is 1 everywhere. Given these constraints, the goal of the optimization is to find a matrix $\matrix{X}$ that minimizes the target function:
$\matrix{f} \space \times \space \matrix{X}$
where $\matrix{f}$ is the distance matrix calculated above, except that it has been "flattened": converted to a column vector of length n_data1 $\times$ n_data2 . $\matrix{X}$ is a flattened form of the binary-valued transformation matrix, where the position of the ones in this matrix maps data2 onto data1 .
An in-depth discussion of integer programming theory is beyond both the scope of this post and the extent of my optimization knowledge, but I'd like to provide further explanation of how I think about the target (minimized) function and constraint equations. In the target function, $\matrix{X}$ selects the set of distances in $\matrix{f}$ that correspond to matched points so that the sum of these values can be determined and minimized. In the first constraint equation, matrix $\matrix{A}$ ensures there is only a single 1 value in each "row" of $\matrix{X}$, so each point in data1 is paired to exactly one point in data2 . Pretending for a moment that the inequality in the second constraint is actually an equality, this equation accomplishes the analogous goal of ensuring each point in data2 is paired to exactly one point in data1 . The inequality enables one of the data sets ( data2 as setup here) to have extra points that are not matched to any points in data1 .
These matrices are setup as follows:
Implementation using CVXOPT and GLPK ¶
Having setup the constraints above, the remaining steps for performing the optimization using CVXOPT are relatively simple. CVXOPT is capable of many types of optimization, thus the variable binVars is used to define the position of all elements in $\matrix{X}$ which are both integer and binary. (For this optimization, that is every element of $\matrix{X}$. Because $\matrix{f}$ is the same length as $\matrix{X}$ and is already defined, its length is used to determine binVars .) Also note that CVXOPT's integer programming function, ilp , does not accept numpy matrices and instead requires its own matrix function that is imported above. Lastly, all the functions use their own variable names, so they are listed as named arguments to eliminate confusion.
The variable output_cvxopt contains several variables, one of which indicates if the optimization converged and, if it did, another variable containing $\matrix{X}$. Normally, it's good practice to check that the optimization converged, but in this case it's known to work. The transformation matrix, X_cvxopt , is reshaped into a two-dimensional matrix so it can easily be used to determine the order of data2 data points that matches them with those in data1 .
Sanity check the optimization results ¶
It is incredibly easy to get dimensions transposed, particularly when matrices have to be flattened and reshaped. Thus, it is critical to check the results. In the above optimization, the peak labels should be identical for each point if the peaks are correctly matched.
Another, more graphical sanity check, involves plotting the data sets on two graphs and connecting the matched pairs.
Implementation using lp_solve ¶
The lp_solve wrapper requires all constraint functions to be entered as a single matrix, so $\matrix{A}$ and $\matrix{C}$ must be combined and, likewise, $\matrix{b}$ and $\matrix{d}$. The relationships ($\leq$, =, and $\geq$) are determined by a vector with a negative, zero, or positive value, respectively.
As with CVXOPT, a set of integers, binVars2 , is used set every value of $\matrix{X}$ to an integer. For lp_solve , the indexing for this set should start at 1 instead of 0 . To ensure that each of these integers is binary, a lower bound of 0 and upper bound of 1 has to be set as well.
Important : lp_solve maximizes the target function. To get the optimization to minimize the function, the value of $\matrix{f}$ must be negated.
The optimization is performed and then the transformation matrix $\matrix{X}$ and matched list are calculated as with CVXOPT.
The data could be checked graphically as well if desired.
This post was written in an IPython notebook, which can be downloaded here , or viewed statically here .
The two solvers, GLPK and lp_solve, are somewhat old and, it would seem, neither particularly fast or robust compared to more modern implementations , but they are well-tested and more than sufficient for my purposes. ↩
I have used a third python library, OpenOpt , which also interfaces with GLPK. It is not demonstrated here as the syntax is similar that utilized by CVXOPT. ↩
Gentle Introduction to Linear Programming by solving Kakuro Puzzles
Sebastian Charmot
This article seeks to strengthen your understanding of linear programming through a fun and practical example using Kakuro puzzles. We will go through how Binary Integer Linear Programming (BILP) can be used to elegantly solve any Kakuro Puzzle . The variables and constraints of the program are explained in detail.
For readers that want to see how to code BILP’s, I also provide an implementation using Python + Gurobi [ 3 ].
Rules of Kakuro
Kakuro puzzles visually resemble crosswords and are played with rules similar to that of Sudoku. The goal of a Kakuro puzzle is to fill all the blank squares.
To fill out a puzzle, we break it down into “crossword clues”, which are called “runs”. For each run, we can only use the numbers 1–9 so that the numbers we enter in a run (consecutive vertical or horizontal empty spaces) add up to the given “clue” . The clue squares include a sum value for runs either across the grid or down the grid.
The length of any “run” can be any integer between 1 and 9 inclusive, so there is no guarantee that every number 1–9 will be used. There must also be no duplicate numbers in each run .
From this example, we also see that “across clues” are shown in the upper quadrant of colored tiles and “vertical clues” are shown in the lower quadrant of colored tiles.
Now that you know the rules, you can try your hand on some puzzles using this website . Solving a few easy puzzles will be a fun way to ensure you know the rules before moving onto how we use integer programming to solve any Kakuro puzzle!
Solving a Kakuro puzzle using BILP offers an extremely succinct and efficient solution that has many advantages over other solution approaches. Other solution approaches involve recursive backtracking, cell ordering, value ordering, projected run pruning, and various hybrids [ 1 ]. Other approaches use a heuristic based system and require a complex pre-computation phase in order to generate time-efficient solutions [ 2 ]. In general, these other solution approaches utilize sophisticated algorithms and involve searching through a large solution space.
U sing a BILP approach allows the problem to be solved not only with a succinct algorithm that uses only five linear constraints but also generates solutions in a time-efficient manner.
Variables of our BILP
Our BILP approach for solving Kakuro puzzles is inspired by linear programming solutions to Sudoku puzzles. To explain our mathematical model, we will refer to the row indices as i and the column indices as j. Both variables start at 1 (just to mess with programmers), and i increases going downwards and j increases going towards the right.
Every empty space on the Kakuro board is represented by a binary variable x_{i,j,k}. The i and j values represent the coordinates of the empty space and k is an integer in the set {1, 2, 3, 4, 5, 6, 7, 8, 9}.
Since x_{i,j,k} is a binary variable, x_{i,j,k} ∈ {0, 1}. If x_{i,j,k} = 1, then the empty space corresponding to coordinates (i, j) = k. In other words, x_{i,j,k} = 1 signals that we are placing the number k in the cell (i,j). These are the only variables used in our model, thus making it a BILP.
We can illustrate our binary variables in the following manner. Due to the board, i and j are constrained by the height and width of the board respectively. Let b_h denote the board height and b_w denote the board width.
Let us illustrate how our binary variables work with the following example.
In this example, we have 4 empty cells across 2 columns and 2 rows which correspond to (2,2), (2,3), (3,2), and (3,3) . Each of these cells can take any integer value, k, where 1 ≤ k ≤ 9. This means that we will have 2 · 2 · 9 = 36 binary variables. Because we have 4 cells to fill, all but 4 of these binary variables have the value 0 . The four binary variables equal to one for our solution are x_{2,2,2}, x_{2,3,7}, x_{3,2,3}, and x_{3,3,9}. This is because the value of cell (2,2) is 2. The value of cell (2,3) is 7. The value of cell (3,2) is 3, and the value of cell (3,3) is 9.
Now that we understand how our binary variables work, let’s look at the linear constraints to solve a Kakuro Puzzle.
Horizontal Clues — Constraints 1 and 2
When we come across a colored cell with a number in the upper right triangle, we have an “across” clue or horizontal run. There are two things we must be aware of when finding the solutions in the empty cells corresponding to a horizontal clue.
- The numbers 1–9 can appear at most once in that horizontal run. We refer to this as the horizontal clue uniqueness constraint .
- The numbers we choose in the empty cells must sum up to the value of the horizontal clue. We refer to this as the horizontal sum constraint .
In order to characterize these considerations into linear constraints, let us define the following variables:
Then, we can translate the two considerations above into the two linear constraints below:
We will now explain in detail what is happening with Constraints (1) and (2). Notice that in both constraints, we fix the current row using i = i_{hc}, because we are working horizontally.
Looking at the summation, we are moving from the lower bound column (j-value) to the upper bound column with a fixed i. This is essentially how we access the empty cells corresponding to the current horizontal clue.
Constraint (1)
For all values of k, we can have at most one of each integer 1–9 appear in the horizontal clue. The term in the summation, is simply the binary variable x_{i,j,k}. The binary variable will only be 1 if we decide to place k in the coordinate (i,j). For every k-value, the summation is moving across the horizontal run and ensuring that at most one k-value is used in the horizontal run. We use ≤ 1 because we are not guaranteed that every k-value is used. It is entirely possible that k will not be used in a given horizontal run. However, we know k cannot be used more than once for one clue!
Constraint (2)
We want the numbers placed in the empty cells of a horizontal run to sum up to the horizontal clue. The term in this nested summation is x_{i,j,k} · k. Again, x_{i,j,k} is only 1 if we place the value k in the cell (i,j), otherwise x_{i,j,k} is 0. By definition of our binary variable, x_{i,j,k} · k is simply the value k when k is placed in the cell (i,j). By summing x_{i,j,k} · k over every k and every cell in the horizontal sum, we get the sum of the values placed in the empty cells of the horizontal run . We want that sum to be equal to the horizontal clue, which is why the nested sum is set to = c_h.
Vertical Clues — Constraints 3 and 4
When we come across a colored cell with a number in the lower left triangle, we have a vertical clue and vertical run.
T he logic for the vertical constraints is the exact same as the horizontal constrains except we are working vertically and not horizontally.
Let us define the following variables:
Then, we devise the two following linear constraints:
The reasoning for both of these constraints is the exact same as the horizontal clues. The difference is that we are now fixing j, since we are moving vertically, and iterating over i values starting at the lower bound row, v_{lb}, to the upper bound row, v_{ub}.
All Empty Cells Must Be Filled — Constraint 5
The vertical and horizontal constraints will guarantee that we don’t use more than one k-value for any given clue and that the values we place in any given run will sum up to the correct value. However, there is still a missing piece.
Without constraint 5, the BILP will generate an invalid solution that solves every clue but does not utilize every empty cell. If there is a way to solve the clues without using every cell, the BILP will find a way to do that.
One of the many joys of working with linear programs is observing how your program will find loopholes unless you provide it with the exact constraints.
Because a valid solution must use every cell once, we require the following final constraint where E represents the set of all (i,j) coordinates that are initially empty.
What is going on in this constraint? Let us fix an empty coordinate (i,j) as (2,2) for example. For a valid solution, we know that the initially empty coordinate (2,2) must have exactly one integer k placed into it. Therefore, the sum of the binary variables x_2,2,k where k starts from 1 and goes to 9, must be exactly 1. Note that this doesn’t specify which k should be chosen, but rather each empty cell must have exactly one value.
Results and Python Implementation
With those 5 simple constraints, we have a BILP that can solve any valid Kakuro puzzle! To see this in effect, I wrote a Python program that implements these constraints, available on my Github [ 3 ].
Using my program which uses the 5 linear constraints described in this article, we can solve even the hardest Kakuro puzzles available on the internet within seconds.
Thank you for reading, and I plan to write another article soon that focuses on my Python + Gurobi implementation of the linear constraints described in this article.
[1] R. P. Davies, P. A. Roach, and S. Perkins. Automation of the solution of kakuro puzzles, 2008. Link
[2] S. Panov and S. Koceski. Solving kakuro puzzle using self adapting har- mony search metaheuristic algorithm. International Journal of Engineering Practical Research, 3(2):34, 2014. doi:10.14355/ijepr.2014.0302.02. Link
[3] https://github.com/SebastianCharmot/Kakuro-Binary-Integer-Linear-Program-Solver

Written by Sebastian Charmot
MS student @ Stanford studying Data Science. Interested in the intersection of AI and climate change.
Text to speech
Stack Exchange Network
Stack Exchange network consists of 183 Q&A communities including Stack Overflow , the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Is there any solver intended specifically for integer and binary variables alone on the optimization model other than solvers for MIP, MILP?
Any solvers which can be integrated in python where we can quickly solve if we have integer and binary variables alone in our model other than normal solvers for MIP, MILP?
- optimization
- mixed-integer-programming
- integer-programming
- $\begingroup$ Can you elaborate on why you don't want to use a MIP or MILP solver? Those solvers usually perform quite well on general pure integer problems. Are they too heavy-weight for your application? Knowing why you don't want to use them may help in suggesting alternatives. $\endgroup$ – Daniel Junglas Commented Aug 6, 2021 at 7:45
- $\begingroup$ It takes too much solver time to solve for MILP where I have complex constraints and large non-zero elements . I thought if the solvers restricts its algorithm or heuristics to branch and bound only for integers, it might perform better. Correct me if I'm wrong. $\endgroup$ – Deepan Commented Aug 6, 2021 at 7:57
- $\begingroup$ Unless you find a solver that is dedicated to your problem type, I would guess that your best option is to go with an existing (potentially commercial) MIP or MILP solver. Maybe it makes sense to discuss your problem or problem formulation rather than looking for a somewhat generic solver alternative. $\endgroup$ – Daniel Junglas Commented Aug 6, 2021 at 8:13
- $\begingroup$ One instance is in the following link where i posted my code, if you can, please check it: or.stackexchange.com/questions/6699/… $\endgroup$ – Deepan Commented Aug 6, 2021 at 8:45
- $\begingroup$ And I agree that it will differ with problem specific and model, the way you formulate it. Lets say if we know that all my variables in my model will be integer or binary and at optimality, all constraints non zero elements, objective value, everything will be integer or binary alone, but MIP/MILP solvers will check for larger solution space even if I can declare my variables are integers or binary, but In a feasible solution, my non zero elements and objective function may take fractional value based on my complexity of the constraints which wont be optimal. $\endgroup$ – Deepan Commented Aug 6, 2021 at 8:53
For binary only there are the following classes of solvers:
- SAT Solvers and MaxSat for optimization
- Pseudo Boolean Programming or Pseudo Boolean optimization
For integer valued there are the following approaches:
- Constraint Programming
- Rephrasing as Boolean Problem provided the search space is finite
- SMT solvers and Optimization modulo theory
As well as local solvers which might be able to solve both.
As for whether such software is callable from Python:
- SAT solvers: yes, for example Lingeling
- Pseudo Boolean solvers: no, as far as i know, but you can generate a problem file a solver like RoundingSAT could work on and read it's output files.
- Contraint programming: yes, see Python constraint
- SMT solvers, yes see Z3Py
- Local solvers, yes see LocalSolver
All those solvers use different proof systems from MILP solvers, so it is possible that they solve certain formulations of certain problems better than MILP solvers. However there is no single approach that dominates MILP on every task.
Your Answer
Sign up or log in, post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged optimization mixed-integer-programming python integer-programming or ask your own question .
- Featured on Meta
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- We spent a sprint addressing your requests — here’s how it went
Hot Network Questions
- I forgot to remove all authors' names from the appendix for a double-blind journal submission. What are the potential consequences?
- Is the text of a LLM determined by a random seed?
- 'adb help' for 'root' says "restart adbd with root permissions", but 'adb root' says "adbd cannot run as root in production builds"
- Why is there not a test for diagonalizability of a matrix
- It was the second, but we were told it was the fifth
- Why did the main wire to my apartment burn before the breaker tripped?
- Can I convert 50 amp electric oven circuit to subpanel, and power oven plus water heater, plus maybe a car charger?
- Was I wrongfully denied boarding for a flight where the airliner lands to a gate that doesn't directly connect to the international part the airport?
- How do we define addition?
- Why did the general choose this as the exact time of attack?
- Challenge the appointment of the prime minister
- Why did Nigel Farage choose Clacton as the constituency to campaign in?
- The meaning of "奪耳" in 《說文解字》
- Manga/manhua/manhwa where the female lead is a princess who is reincarnated by the guard who loved her
- Weather on a Flat, Infinite Sea
- Everything has a tiny nuclear reactor in it. How much of a concern are illegal nuclear bombs?
- How to pin to the Task Bar the Device Manager on Windows 11?
- Why was this a draw?
- Transhumans, posthumans, and AI attacked by baseline humans
- Can the differential be unitless while the variable have an unit in integration?
- Why are responses to an attack in a cycling race immediate?
- Simulate slow disks in KVM to see effect of LVM cache in test setup
- Is a desert planet with a small habitable area possible?
- Minimum number of select-all/copy/paste steps for a string containing n copies of the original
Navigation Menu
Search code, repositories, users, issues, pull requests..., provide feedback.
We read every piece of feedback, and take your input very seriously.
Saved searches
Use saved searches to filter your results more quickly.
To see all available qualifiers, see our documentation .
- Notifications You must be signed in to change notification settings
A Binary Integer Linear Solver written in Python using Gurobi that outputs a visual solution to any valid Kakuro puzzle
SebastianCharmot/Kakuro-Binary-Integer-Linear-Program-Solver
Folders and files.
| Name | Name | |||
|---|---|---|---|---|
| 2 Commits | ||||
Repository files navigation

Binary Integer Linear Program (BILP) to Solve Kakuro Puzzles
A Python implementation of a BILP that solves any Kakuro puzzle and outputs a visual solution.
Getting Started
Initial population, fitness function, euclidean distance, crossover 1 - blending, crossover 2 - crossover point, crossover 3 - pixel-wise, mutation 1 - random shape, mutation 2 - adding a constant, experimentation, introduction to genetic algorithms.
In this section, I give a general overview of what a genetic algorithm is. Readers that are familiar with this concept can skip to the next section.
A genetic algorithm is an optimization tool inspired by Darwin's theory of evolution. The algorithm mimics the process of natural selection, which chooses the fittest individuals from a population to create offspring and populate future generations.
A genetic algorithm consists of the main components below. Click on any of the triangles to read a definition of each.
- Initial Population The genetic algorithm starts with a group of individuals, referred to as the initial population. Each individual is a solution for the target that we are optimizing for. Typically, the individuals of the initial population are created randomly, assuming no prior knowledge about the solution. Because the individuals of the initial population are created randomly, they are likely poor solutions. However, their sole purpose is to serve as the building blocks for future generations.
- Fitness Function Once an initial population is created, the individuals are evaluated based on a fitness function. The fitness function is a metric that evaluates what our genetic algorithm is seeking to optimize. In the classic genetic algorithm example of binary strings with a target, this fitness function might be how many binary strings have the correct value. In this case, a higher fitness function is a string that is "more fit" and closer to the optimal value.
- Selection Criteria The selection criteria determines which individuals from the population are chosen to be parents for the next generation. Typically, we want to select individuals with stronger fitness. However, if we only select individuals with very strong fitness, we will lose some biodiversity. In terms of our algorithm, we want to maintain a certain level of stochasticity within each population to avoid falling into local minima. The classic way parent selection is done is via tournament selection. In essence, X individuals are selected from the total population and the most fit individual from those X tournament participants is chosen to be the parent. We can see that the lower X is, the more stochasticity and biodiversity we introduce into our parent selection. Finding the optimal balance between selecting generally more fit individuals while also maintaining a diverse set of parents is one of the challenging but fun aspects of genetic algorithms.
- Crossover The crossover methods we implement determine how the offspring are created once we have selected parents. Typically two parents are chosen to create offspring. The purpose of a crossover function is to try to combine the attributes of the two parents into a child that is more fit. In order to do so, a popular method is simply to take the first half of parent(1) and combine it with the second half of parent(2). A random "crossover point" can also be used, meaning that parent(1) is used up until the crossover point and then parent(2) is used after the crossover point. Regardless of how crossover is implemented, the hope is that the child will incorporate elements of both parents and have a higher fitness.
- Mutation Mutations are relatively low probability operations that slightly alter an offspring. The purpose of mutations are to introduce stochasticity, which can help combat local optima.
Putting together these components, we have the foundation for a genetic algorithm. We combine them in the following order. First, an initial population is seeded. It's individuals are evaluated by the fitness function, and then our selection criteria chooses fit parents to crossover and populate the next population. Each time a child is produced, there is a potential it will mutate.
We can repeat the process of creating future generations for a set number of generations or until an optimal solution is achieved.
Now that we have introduced a genetic algorithm, we can dive into my genetic algorithm that seeks to recreate an image.
Using the following libraries:
- Pillow (Image manipulation)
- Matplotlib (Image display)
- Numpy (Perform vectorized image manipulation and calculations)
- Colour (Delta E color difference calculations)
The first step is installing the necessary libraries. This can be done by running the following:
Getting started with the genetica algorithm is as simple as instantiating a GP class from GP.py as the following:
The arguments of the run_gp method are (size of the initial population, number of generations to run) . For most of my experiments, an initial population of size 100 and 5,000 generations was enough to produce great results. By vectorizing the majority of the image manipulations, I am able to run those settings comfortably on my laptop with a run-time of several minutes.
Hyperparameters
When tuning hyperparameters, the variables of interest are the following:
- Size of the initial population
- The lower and upper bound on the number of random shapes
- Whether to use Delta_E or Euclidean Distance
- Altering the size of a tournament
- Different probabilistic combinations
- Varying the probability of a mutation occurring
- Changing the probability of using mutation 1 versus mutation 2
We will now dive into the code to change each of the following hyperparameters.
Changing the size of the initial population can be done by the first argument passed into the GP class' GP.run_gp method.
Each individual is created by the Individual class found in Individual.py . When a random individual is created, it is given a random background color. Then, a random number of polygons of random sides with random color is added onto that background.
All of this is within the Individual's create_random_image_array method.
Below are examples of individuals created this way.

I experimented with two main fitness functions. The fitness function is found within the Individual class.
A relatively straightforward implementation where I take the Euclidean distance between the RGB values of two pixels. Then, I perform this operation across the entire image and take the mean. To use Euclidean distance:
However, Euclidean distance has one main disadvantage. It is the fact that our eyes do not perceive difference in RGB values according to Euclidan distance. The example below illustrates this.

In an attempt to quantify how human eyes detect differences in color, scientists devised the Delta_E metric.
Delta_E is a more robust measurement of color difference true to the human eye. It was developed by the International Commission on Illumination and is considered the standard color difference measurement tool. To use the Delta_E fitness function, we simply leverage the colour library in the following manner:
My experiments indicated that Delta_E generated better outputs virtually every single time.
I implemented tournament selection to select parents. I randomly sampled the population given a tournament size and selected the fittest individual to be the winner of the tournament.
To experiment with different tournament sizes, alter the tournament_size variable. I had the most success with a tournament size between 6-8% of the total population size.
I implemented 3 unique crossover functions and experimented with probabilistic blends of all 3. Below, I describe each crossover function and give an example.
In this functon, I assign opacity $x$ to $\text{parent} {1}$ and assign opacity $1-x$ to $\text{parent} {2}$. Then we overlay both of them to create the child. If $x$ is 0, a copy of $\text{parent} {1}$ is produced. If $x$ is 1, a copy of $\text{parent} {2}$ is produced.
To determine $x$ , I sample a uniform distribution where $x \in (0,1)$ . One advantage of not fixing $x = 0.5$ is that this introduces stochasticity to the crossover function and can produce different children given the same parents.
Below is an example of what this look like:

In this approach, we select a random row or column to be a crossover point. Everything up until that row or column is from $\text{parent} {1}$ and everything including and after that row or column is from $\text{parent} {2}$. Once again, this row or column is selected from a uniform distribution. The two examples below illustrate a row crossover point and a column crossover point respectively.

I assigned an equal chance for Crossover 2 to be done horizontally or vertically. It would be interesting to test diagonal crossover lines but for my experiments, I only used horizontal or vertical crossovers.
For this crossover function, each pixel in the child is selected randomly from either $\text{parent} {1}$ or $\text{parent} {2}$.
This technique performs well but ends up creating images that look granulated as you can see in the example below. As a result, I didn't utilize this crossover function much.

I developed 2 different mutation functions that would slightly modify an individual.
To perform this mutation, I superimpose a random number of shapes of random color onto an individual.
The result of this mutation can be seen below.

In this mutation, I select a random subset of pixels and add a constant to their RGB values.
The results of this kind of mutation can be seen in the figure below.

It's effects are relatively subtle and did not seem to be an effective mutation operation. It also introduces the effect of "pixelation" which I believe tend to decrease the visually appearance of individuals.
Given all this information about how the specific hyperparameters work, you can start to experiment with your own images. As a baseline, I will provide the hyperparameters that worked best for me:
- Size of 100
- Each with [3, 6] shapes of random color
- Only Delta_E
- Tournament size of 6
- Using a probabilistic mix of 30% crossover 1 (blending) and 60% crossover 2 (crossover)
- Using a 10% chance for mutation 1 (adding shape)
- Anywhere between 5,000 and 10,000

- Python 100.0%
- Crimson Careers
- For Employers
- Harvard College
- Harvard Kenneth C. Griffin Graduate School of Arts & Sciences
- Harvard Extension School
- Premed / Pre-Health
- Families & Supporters
- Faculty & Staff
- Prospective Students
- First Generation / Low Income
- International Students
- Students of Color
- Students with Disabilities
- Undocumented Students
- Explore Interests & Make Career Decisions
- Create a Resume/CV or Cover Letter
- Expand Your Network
- Engage with Employers
- Search for a Job
- Find an Internship
- January Experiences (College)
- Find & Apply for Summer Opportunities Funding
- Prepare for an Interview
- Negotiate an Offer
- Apply to Graduate or Professional School
- Access Resources
- AI for Professional Development and Exploration
- Arts & Entertainment
- Business & Entrepreneurship
- Climate, Sustainability, Environment, Energy
- Government, Int’l Relations, Education, Law, Nonprofits
- Life Sciences & Health
- Technology & Engineering
- Still Exploring
- Talk to an Advisor
45 Common Coding Interview Questions
- Share This: Share 45 Common Coding Interview Questions on Facebook Share 45 Common Coding Interview Questions on LinkedIn Share 45 Common Coding Interview Questions on X
45 Common Coding Interview Questions was originally published on Forage .

A coding interview can be nerve-racking, but it’s an essential part of the technical interview process to demonstrate your programming skills and knowledge of coding concepts. While the exact questions a technical recruiter might ask vary depending on what kind of role you’re applying for, there are some common coding interview questions you can prepare for to ace the interview. We’ll cover:
Programming Interview Questions
Conceptual coding interview questions, general coding interview questions.
A coding interview typically starts with an assessment of your computer programming skills. This assessment might be a whiteboard challenge or coding test.
What Is a Whiteboard Challenge?
A whiteboard challenge is when you’re given a coding challenge during a live interview . You solve the problem in front of the interviewer and explain your process as you work on the challenge.
You can use the UMPIRE method to approach these problems:
U: Understand the problem M: Match the problem with the interviewer P: Plan your approach and solution I: Implement your solution R: Review your solution E: Evaluate your solution
To prepare for a whiteboard challenge, “practice talking through your problem-solving process ,” says Archie Payne, president of CalTek Staffing, an IT and technical staffing firm. “Interviewers don’t just want to see that candidates can complete the test task, they also want to get insights into how candidates approach the process. A good way to prepare is to pretend you’re teaching a programming class, and practice how you’d explain and demonstrate key concepts to someone who doesn’t know them.”
It’s less about solving everything right the first time (or even at all) and more about learning how you approach problems and solve challenges.
And what happens if you don’t know the answer? Don’t panic.
“Be honest that this is a gap in your knowledge,” Payne says. “Take a moment to think critically about the problem and the ways you’d likely approach it, then explain that process to the interviewer. Hiring managers don’t necessarily expect entry-level candidates to have all the answers, but they do want to hire someone who’s self aware about what they do and don’t know, and willing to learn and try new things.”
What Is an Independent Coding Test?
An indepdent coding test focuses on your ability to code and solve problems within a given time frame. You may have an independent coding test after your whiteboard test or before as part of a screening.
The company will give you a link to a common code editor, and you can choose what programming language you want to write in. Before you start the test, you’ll know how long you have to complete it and whether you’ll be able to leave the platform during the test. Make sure you do the test in a quiet environment where you won’t have distractions.
To prepare for this part of the interview, “simulate interview conditions,” Mohit Maheshwari, co-founder at NMG Technologies, a full-service IT company, says. “Practice coding on a whiteboard or a blank sheet of paper, as this is how you will be doing it during the interview. Get used to writing code without the aid of an IDE [integrated development environment] or compiler.”

JPMorgan Chase Software Engineering
Practice basic programming skills with a Python project.
Avg. Time: 5 hours
Skills you’ll build: Python, Git, React, Typescript, technical communication
Common Programming Interview Questions
What questions will you get in a whiteboard challenge or independent coding test? Here are some examples:
- How do you reverse a string?
- How do you determine if a string is a palindrome?
- How do you calculate the number of numerical digits in a string?
- How do you find the count for the occurrence of a particular character in a string?
- How do you find the non-matching characters in a string?
- How do you find out if the two given strings are anagrams?
- How do you calculate the number of vowels and consonants in a string?
- How do you total all of the matching integer elements in an array?
- How do you reverse an array?
- How do you find the maximum element in an array?
- How do you sort an array of integers in ascending order?
- How do you print a Fibonacci sequence using recursion?
- How do you calculate the sum of two integers?
- How do you find the average of numbers in a list?
- How do you check if an integer is even or odd?
- How do you find the middle element of a linked list?
- How do you remove a loop in a linked list?
- How do you merge two sorted linked lists?
- How do you implement binary search to find an element in a sorted array?
- How do you print a binary tree in vertical order?

Forage Find
LeetCode is a great resource for practicing these types of questions. You can create a free account and practice hundreds of coding questions you might get in an interview.
The recruiter or hiring manager will also ask conceptual coding interview questions to learn whether you’re familiar with the concepts you’ll be working with.
“Expect questions on basic data structures such as arrays, linked lists, trees, and graphs, as well as common algorithms like sorting and searching,” Maheshwari says.
To prepare for these questions, refamiliarize yourself with these concepts. Then, you can practice by explaining them clearly to someone who doesn’t have technical knowledge.
Examples of these questions include:
- What is a data structure?
- What is an array?
- What is a linked list?
- What is the difference between an array and a linked list?
- What is LIFO?
- What is FIFO?
- What is a stack?
- What are binary trees?
- What are binary search trees?
- What is object-oriented programming?
- What is the purpose of a loop in programming?
- What is a conditional statement?
- What is debugging?
- What is recursion?
- What are the differences between linear and non-linear data structures?
>>MORE: Learn explanations of common software engineering technical concepts with entry-level software engineering interview questions (and answers) .
Outside of programming questions and questions about technical concepts, you might answer questions about your general experience, like how you learned to code, behavioral interview questions , and how you keep your skills fresh.
Examples of general common coding interview questions include:
- What programming languages do you have experience working with?
- Describe a time you faced a challenge in a project you were working on and how you overcame it.
- Walk me through a project you’re currently or have recently worked on.
- Give an example of a project you worked on where you had to learn a new programming language or technology. How did you go about learning it?
- How do you ensure your code is readable by other developers?
- What are your interests outside of programming?
- How do you keep your skills sharp and up to date?
- How do you collaborate on projects with non-technical team members?
- Tell me about a time when you had to explain a complex technical concept to a non-technical team member.
- How do you get started on a new coding project?
“Be prepared to explain your expertise in the languages you know and what types of projects you’ve completed using them,” Payne says. “The ability to troubleshoot and correct issues as you go is a key skill for programmers at all career levels. The best answer will focus on the steps you take to diagnose and fix issues, rather than the intricate details of the specific problem you’re describing.”
Common Coding Interview Questions: The Bottom Line
Programming interview questions generally come in three different forms: practical coding tests, questions about technical concepts, and general questions about your experience. To ace a coding interview, prepare carefully for each section: practice problems, review concepts, and use the STAR method to shape answers about your experience.
Are you getting ready for a coding interview? Practice sample coding problems with matrices and arrays and learn what hiring managers look for in technical interviews with Girls Who Code’s Technical Interview Prep .
Image credit: Canva
The post 45 Common Coding Interview Questions appeared first on Forage .
- Stack Overflow for Teams Where developers & technologists share private knowledge with coworkers
- Advertising & Talent Reach devs & technologists worldwide about your product, service or employer brand
- OverflowAI GenAI features for Teams
- OverflowAPI Train & fine-tune LLMs
- Labs The future of collective knowledge sharing
- About the company Visit the blog
Collectives™ on Stack Overflow
Find centralized, trusted content and collaborate around the technologies you use most.
Q&A for work
Connect and share knowledge within a single location that is structured and easy to search.
Get early access and see previews of new features.
Binary and Integer Program in Python
I have a binary/integer program that I am trying to solve using milp in Python. Below the image and below is the code I have so far. When I run it, I get
I believed I accounted for the upper and lower bounds in the "bounds" variable. But apparently not. What is missing?

- optimization
- linear-programming
- integer-programming
There are two issues with your code. First, to disable bounds or define "unbounded bounds", one should use np.inf or -np.inf instead of None .
Second, you are currently giving a list of tuples to scipy.optimize.Bounds which does not work. Instead you should provide a list of the lower bounds and a list for the upper bounds.
To resolve these issues, you can change the last part of your code to:
Instead of the list comprehension you could also use the zip function for a more concise solution:
or directly
Personally, I prefer the solution using list comprehension as it is clearer to the reader what is happening and with lists of this length, performance is not really an issue.
- Ah! I see, thank you! Now I see that my program is not set up correctly, which is a completely different issue. – gunsnfloyd Commented Mar 16 at 1:42
Your Answer
Reminder: Answers generated by artificial intelligence tools are not allowed on Stack Overflow. Learn more
Sign up or log in
Post as a guest.
Required, but never shown
By clicking “Post Your Answer”, you agree to our terms of service and acknowledge you have read our privacy policy .
Not the answer you're looking for? Browse other questions tagged python math optimization linear-programming integer-programming or ask your own question .
- Featured on Meta
- We spent a sprint addressing your requests — here’s how it went
- Upcoming initiatives on Stack Overflow and across the Stack Exchange network...
- What makes a homepage useful for logged-in users
- The [lib] tag is being burninated
Hot Network Questions
- Newbie trying to write a simple script to automate command
- How much does a factory reset help in hiding a device's identification details?
- Can I SSH with key and then have a simple password for the sudo user?
- Setting Stack Pointer on Bare Metal Rust
- PCIe digest explanation
- Using 50 Ω coax cable instead of passive probe
- Can the differential be unitless while the variable have an unit in integration?
- Star alliance lounge at Luxembourg?
- Manga/manhua/manhwa where the female lead is a princess who is reincarnated by the guard who loved her
- Mathematics & Logic (Boolean Algebra)
- Job talk Q&A: handling the room vs. being respectful
- Are there any video/audio recordings of the launch of sputnik 1?
- Simulate slow disks in KVM to see effect of LVM cache in test setup
- Could mathematical truths have been otherwise?
- What is the reason for using decibels to measure sound?
- How to photograph the lettering on a bronze plaque?
- Question about NMAP HTTP Verb Tampering
- Do you always experience the gravitational influence of other mass as you see them in your frame?
- What does "that" in "No one ever meant that, Drax" refer to?
- If I Trace "Pickup", will I pickup?
- Challenge the appointment of the prime minister
- Topology of the projective space
- firefox returns odd results for file:/// or file:///tmp
- Why does black have a higher win rate here?

COMMENTS
Hands On Integer (Binary) Linear Optimization using Python ... In fact, it exists a very well known algorithm to solve this kind of problems, ... Exploring the classical discrete optimization problem through custom constructive heuristics and integer programming in Python. Nov 13, 2023. 2. Bo Yuan, Ph.D.
Constrain the problem such that it can be solved by a more general linear programming solver. Interface Python with MATLAB so as to make direct use of bintprog. python; matlab; linear-programming ... A linear program with both binary/integer variables AND continuous variables is called an MILP (Mixed Integer Linear Program). The terms "integer ...
A particularly important kind of integer variable is the binary variable. ... You now know what linear programming is and how to use Python to solve linear programming problems. You also learned that Python linear programming libraries are just wrappers around native solvers. When the solver finishes its job, the wrapper returns the solution ...
A Python function which computes this gradient is constructed by the code-segment: ... The trust-ncg algorithm is a trust-region method that uses a conjugate gradient algorithm to solve the trust-region ... Mary E. Hribar, and Jorge Nocedal. 1999. An interior point algorithm for large-scale nonlinear programming. SIAM Journal on Optimization 9. ...
linprog. #. Linear programming: minimize a linear objective function subject to linear equality and inequality constraints. Linear programming solves problems of the following form: where x is a vector of decision variables; c , b u b, b e q, l, and u are vectors; and A u b and A e q are matrices. Alternatively, that's: Note that by default ...
Integer Programming in Python. We'll use integer programming to make optimal decisions. Photo from Unsplash. Integer Programming (IP) problems are optimization problems where all of the variables are constrained to be integers. IP problems are useful mathematical models for how to best allocate one's resources.
Python MIP is a collection of Python tools for the modeling and solution of Mixed-Integer Linear programs (MIPs). MIP syntax was inspired by Pulp. Just like CyLP it also provides access to advanced solver features like cut generation, lazy constraints, MIPstarts and solution Pools. Porting Pulp and Gurobi models should be quite easy.
When you ignore the integer constraint, you're doing what's called "linear programming relaxation" (LP relaxation) . Solving the LP relaxation will provide a (possibly non-integer) \ (\mathbf {x}\). We'll use scipy's linprog function to solve the LP relaxation. Here's how linprog 's arguments map to our formulation.
To use the Exact Python interface with optimal binaries for your machine (and the option to include SoPlex in the binary), compile as a shared library and install it with your package manager. E.g., on Linux systems, running pip install . in Exact's root directory should do the trick. On Windows, uncomment the build options below # FOR WINDOWS ...
Since methods for solving integer programs include approaches like relaxing the integer variables to continuous variables, then solving using a branch-and-bound (or branch-and-cut, or other) scheme, from an implementation perspective, implementing an integer programming solver frequently means mixed-integer programs can also be solved. $\endgroup$
The SCIP Optimization Suite is a toolbox for generating and solving mixed integer nonlinear programs, in particular mixed integer linear programs, and constraint integer programs. It consists of the following parts: SCIP. mixed integer (linear and nonlinear) programming solver and constraint programming framework.
An integer linear program solver using a Lagrange decomposition into binary decision diagrams. Lagrange multipliers are updated through min-marginal averaging (a form of dual block coordinate ascent). Sequential and parallel CPU solvers are provided as well as a massively parallel GPU implementation.
A Binary Integer Linear Solver written in Python using Gurobi that outputs a visual solution to any valid Kakuro puzzle. kakuro-solver integer-linear-programming binary-integer-programming Updated Sep 14, 2022; Python; lucianoSF / KNP-TS Star 0. Code Issues Pull requests ...
This notebook demonstrates how to use python to interface with two open source packages for binary integer programming, GLPK and lp_solve.These packages are demonstrated using two python libraries, CVXOPT, which interacts with GLPK, and lp_solve's own python interface.An example for matching five x,y-coordinate pairs from two different data sets is shown for each library.
1. This article seeks to strengthen your understanding of linear programming through a fun and practical example using Kakuro puzzles. We will go through how Binary Integer Linear Programming ...
A Binary Integer Linear Solver written in Python using Gurobi that outputs a visual solution to any valid Kakuro puzzle. ... Add a description, image, and links to the binary-integer-programming topic page so that developers can more easily learn about it. Curate this topic Add this topic to your repo To associate your repository with ...
As well as local solvers which might be able to solve both. As for whether such software is callable from Python: SAT solvers: yes, for example Lingeling; Pseudo Boolean solvers: no, as far as i know, but you can generate a problem file a solver like RoundingSAT could work on and read it's output files. Contraint programming: yes, see Python ...
They get converted to binary when your program starts and are only converted back to decimal when you use something like str() or print - John La Rooy. Commented Oct 6, ... Converting integer to binary in Python. 3. Incrementing a binary number in python. 6. Using Python to convert integer to binary. 2.
A Binary Integer Linear Solver written in Python using Gurobi that outputs a visual solution to any valid Kakuro puzzle Topics kakuro-solver integer-linear-programming binary-integer-programming
Let's try to implement the genetic algorithm in Python. Problem Definition. Problem: Compute on the specific function; f(x) = x^2f(x) = x^2; only integer values of x. Fitness Function: For the case of a chromosome that is binary being x, an example of the fitness function could be f(x)= x^2.
45 Common Coding Interview Questions was originally published on Forage.. A coding interview can be nerve-racking, but it's an essential part of the technical interview process to demonstrate your programming skills and knowledge of coding concepts. While the exact questions a technical recruiter might ask vary depending on what kind of role you're applying for, there are some common ...
Instead you should provide a list of the lower bounds and a list for the upper bounds. To resolve these issues, you can change the last part of your code to: # Define bounds for each variable (0 <= xi <= 1 for binary variables, 0 <= yij) x_bounds = [(0, 1)] * 9 # Bounds for the x variables.