High Impact Tutoring Built By Math Experts
Personalized standards-aligned one-on-one math tutoring for schools and districts
In order to access this I need to be confident with:

Solving inequalities
Here you will learn about solving inequalities, including how to solve linear inequalities, identify integers in the solution set, and represent solutions on a number line.
Students will first learn about solving simple inequalities as part of expressions and equations in 6th grade math and expand that knowledge in 7th grade math.
What is solving inequalities?
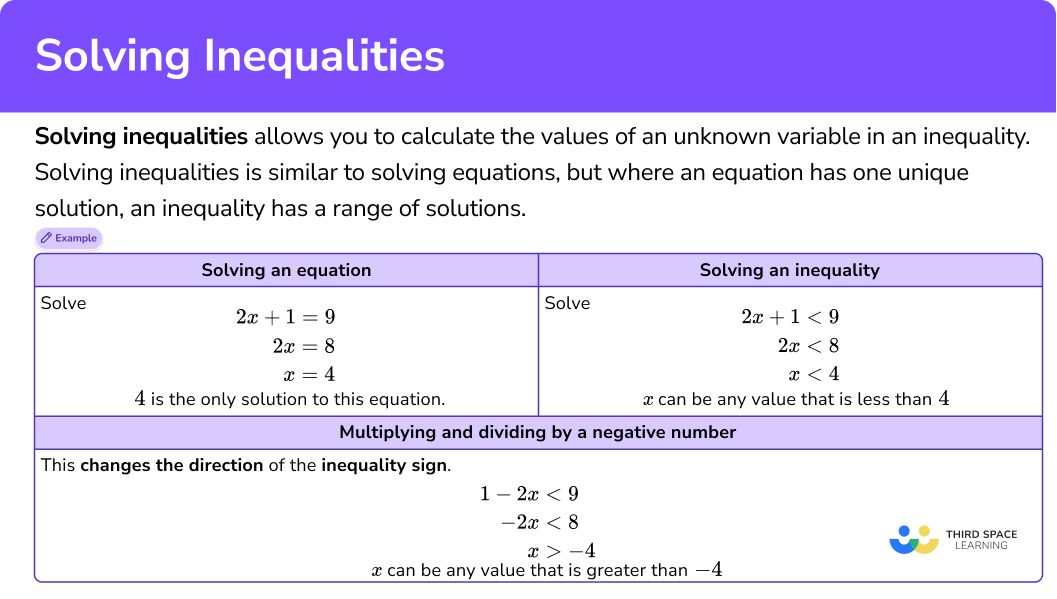
Solving inequalities allows you to calculate the values of an unknown variable in an inequality.
Solving inequalities is similar to solving equations, but where an equation has one unique solution, an inequality has a range of solutions.
In order to solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.
For example,
Solve \begin{aligned} 2x + 1 &= 9 \\ 2x &= 8 \\ x&= 4 \end{aligned} 4 is the only solution to this | Solve \begin{aligned} 2x + 1 &< 9 \\ 2x &< 8 \\ x&< 4 \end{aligned} x can be any value that is less |
This of the x can be any value that is greater than -4. |
[FREE] Solving Inequalities Worksheet (Grade 6 to 8)
Use this worksheet to check your grade 6 to 8 students’ understanding of solving inequalities. 15 questions with answers to identify areas of strength and support!
Common Core State Standards
How does this relate to 6th grade and 7th grade math?
- Grade 6 – Expressions and Equations (6.EE.B.8) Write an inequality of the form x > c or x < c to represent a constraint or condition in a real-world or mathematical problem. Recognize that inequalities of the form x > c or x < c have infinitely many solutions; represent solutions of such inequalities on number line diagrams.
- Grade 7 – Expressions and Equations (7.EE.4b) Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the context of the problem. For example: As a salesperson, you are paid \$50 per week plus \$3 per sale. This week you want your pay to be at least \$100. Write an inequality for the number of sales you need to make, and describe the solutions.
How to solve inequalities
In order to solve inequalities:
Rearrange the inequality so that all the unknowns are on one side of the inequality sign.
Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
Write your solution with the inequality symbol.
Solving linear inequalities examples
Example 1: solving linear inequalities.
4 x+6<26
In this case you are subtracting 6 from both sides.
\begin{aligned} 4x+6&<26\\ 4x&<20 \end{aligned}
This leaves 4x on the left side of the inequality sign and 20 on the right side.
2 Rearrange the inequality by dividing by the \textbf{x} coefficient so that \textbf{‘x’} is isolated.
In this case you need to divide both sides by 4.
\begin{aligned} 4x&<20\\ x&<5 \end{aligned}
This leaves x on the left side of the inequality sign and 5 on the right side.
3 Write your solution with the inequality symbol.
Any value less than 5 satisfies the inequality.
Example 2: solving linear inequalities
5x-4 \geq 26
In this case you need to add 4 to both sides.
\begin{aligned} 5x-4&\geq26\\ 5x&\geq30 \end{aligned}
This leaves 5x on the left side of the inequality sign and 30 on the right side.
In this case you need to divide both sides by 5.
\begin{aligned} 5x&\geq30\\ x&\geq6 \end{aligned}
This leaves x on the left side of the inequality sign and 6 on the right side.
Any value greater than or equal to 6 satisfies the inequality.
Example 3: solving linear inequalities with parentheses
3(x-4)\leq12
Let’s start by expanding the parentheses.
3x-12\leq12
Then you need to add 12 to both sides.
\begin{aligned} 3x-12&\leq12\\ 3x&\leq24 \end{aligned}
This leaves 3x on the left side of the inequality sign and 24 on the right side.
In this case you need to divide both sides by 3.
\begin{aligned} 3x&\leq24\\ x&\leq8 \end{aligned}
This leaves x on the left side of the inequality sign and 8 on the right side.
Any value less than or equal to 8 satisfies the inequality.
Example 4: solving linear inequalities with unknowns on both sides
5x-6 > 2x + 15
In this case you need to subtract 2x from both sides.
\begin{aligned} 5x-6&>2x+15\\ 3x-6&>15 \end{aligned}
This leaves 3x-6 on the left side of the inequality sign and 15 on the right side.
Rearrange the inequality so that \textbf{‘x’} s are on one side of the inequality sign and numbers on the other.
In this case you need to add 6 to both sides.
\begin{aligned} 3x-6&>15\\ 3x&>21 \end{aligned}
This leaves 3x on the left side of the inequality sign and 21 on the right side.
\begin{aligned} 3x&>21\\ x&>7 \end{aligned}
This leaves x on the left side of the inequality sign and 7 on the right side.
Any value greater than 7 satisfies the inequality.
Example 5: solving linear inequalities with fractions
\cfrac{x+3}{5}<2
Rearrange the inequality to eliminate the denominator.
In this case you need to multiply both sides by 5.
\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10 \end{aligned}
In this case you need to subtract 3 from both sides.
\begin{aligned} \cfrac{x+3}{5}&<2\\ x+3&<10\\ x&<7 \end{aligned}
Any value less than 7 satisfies the inequality.
Example 6: solving linear inequalities with non-integer solutions
In this case you need to subtract 6 from both sides.
\begin{aligned} 6x+1&\geq4\\ 6x&\geq3 \end{aligned}
In this case you need to divide both sides by 6.
\begin{aligned} 6x+1&\geq4\\ 6x&\geq3\\ x&\geq\cfrac{3}{6} \end{aligned}
This can be simplified to \, \cfrac{1}{2} \, or the decimal equivalent.
x\geq\cfrac{1}{2}
Any value greater than or equal to \, \cfrac{1}{2} \, satisfies the inequality.
Example 7: solving linear inequalities and representing solutions on a number line
Represent the solution on a number line:
2x-7 < 5
In this case you need to add 7 to both sides.
\begin{aligned} 2x-7&<5\\ 2x&<12 \end{aligned}
In this case you need to divide both sides by 2.
\begin{aligned} 2x-7& <5\\ 2x& <12\\ x& < 6 \end{aligned}
Represent your solution on a number line.
Any value less than 6 satisfies the inequality. An open circle is required at 6 and the values lower than 6 indicated with an arrow.

Example 8: solving linear inequalities with negative x coefficients
In this case you need to subtract 1 from both sides.
\begin{aligned} 1-2x & <7 \\ -2x & <6 \end{aligned}
In this case you need to divide both sides by negative 2.
6 \div-2=-3
Change the direction of the inequality sign.
Because you divided by a negative number, you also need to change the direction of the inequality sign.
\begin{aligned} 1-2x & <7 \\ -2x & <6 \\ x &>-3 \end{aligned}
Example 9: solving linear inequalities and listing integer values that satisfy the inequality
List the integer values that satisfy:
3 < x+1\leq8
In this case you need to subtract 1 from each part.
\begin{aligned} 3&<x+1\leq8\\ 2&<x\leq7\\ \end{aligned}
List the integer values satisfied by the inequality.
2<x\leq7
2 is not included in the solution set. 7 is included in the solution set. The integers that satisfy this inequality are:
3, 4, 5, 6, 7
Example 10: solving linear inequalities and listing integer values that satisfy the inequality
7\leq4x\leq20
In this case you need to divide each part by 4.
\begin{aligned} 7\leq \, & 4x\leq20\\ \cfrac{7}{4}\leq & \; x \leq5 \end{aligned}
\cfrac{7}{4} \leq x \leq 5
\cfrac{7}{4} \, is included in the solution set but it is not an integer.
The first integer higher is 2.
5 is also included in the solution set.
The integers that satisfy this inequality are:
Example 11: solving linear inequalities and representing the solution on a number line
-3<2x+5\leq7
In this case you need to subtract 5 from each part.
\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2 \end{aligned}
Rearrange the inequality so that \textbf{‘x’} is isolated. In this case you need to divide each part by \bf{2} .
\begin{aligned} -3<2x+5&\leq7\\ -8<2x&\leq2\\ -4<x&\leq1 \end{aligned}
Represent the solution set on a the number line
-4<x\leq1
-4 is not included in the solution set so requires an open circle. 1 is included in the solution set so requires a closed circle.
Put a solid line between the circles to indicate all the values that satisfy the solution set.

Teaching tips for solving inequalities
- Students should master solving simple inequalities (one-step inequalities) before moving on to two-step inequalities (or multi-step inequalities).
- Foster student engagement by practicing solving inequalities through classroom games such as BINGO rather than daily worksheets.
- Student practice problems should have a variety of inequalities such as inequalities with fractions, negative numbers, and parentheses. (see examples above)
Easy mistakes to make
- Solutions as inequalities Not including the inequality symbol in the solution is a common mistake. An inequality has a range of values that satisfy it rather than a unique solution so the inequality symbol is essential. For example, when solving x + 3 < 7 giving a solution of 4 or x = 4 is incorrect, the answer must be written as an inequality x < 4 .
- Balancing inequalities Errors can be made with solving equations and inequalities by not applying inverse operations or not balancing the inequalities. Work should be shown step-by-step with the inverse operations applied to both sides of the inequality. For example, when solving x + 3 < 7 , adding 3 to both sides rather than subtracting 3 from both sides.
Related inequalities lessons
- Inequalities
- Linear inequalities
- Inequalities on a number line
- Graphing inequalities
- Quadratic inequalities
- Greater than sign
- Less than sign
Practice solving inequalities questions
3x+7 < 31

\begin{aligned} 3x+7&<31\\ 3x&<24\\ x&<8 \end{aligned}
\begin{aligned} 4x-3&\geq25\\ 4x&\geq28\\ x&\geq7 \end{aligned}
2(x-5)\leq8
\begin{aligned} 2(x-5)&\leq8\\ 2x-10&\leq8\\ 2x&\leq18\\ x&\leq9 \end{aligned}
6x-5 > 4x + 1
\begin{aligned} 6x-5&>4x+1\\ 2x-5&>1\\ 2x&>6\\ x&>3 \end{aligned}
\cfrac{x-4}{2}>6
\begin{aligned} \cfrac{x-4}{2}&>6\\ x-4&>12\\ x&>16 \end{aligned}
\begin{aligned} 8x+1&\geq3\\ 8x&\geq2\\ x&\geq\cfrac{2}{8}\\ x&\geq\cfrac{1}{4} \end{aligned}
7. Represent the solution on a number line.
5x-2 < 28

\begin{aligned} 5x-2&<28\\ 5x&<30\\ x&<6 \end{aligned}
An open circle is required and all values less than 6 indicated.
2-3x > 14
\begin{aligned} 2-3x &>14 \\ -3x &>12 \\ x &< -4 \end{aligned}
Change the direction of the inequality sign as you have divided by a negative number.
9. List the integer values that satisfy:
2<x+3\leq5
\begin{aligned} 2<x&+3\leq5\\ -1< \, &x\leq2 \end{aligned}
-1 is not included in the solution set as is greater than -1.
2 is included in the solution set as x is less than or equal to 2.
10. List the integer values that satisfy:
4\leq3x\leq21
\begin{aligned} 4\leq3&x\leq21\\ \cfrac{4}{3} \, \leq \, &x\leq7 \end{aligned}
The first integer greater than \, \cfrac{4}{3} \, is 2.
7 is included in the solution set as x is less than or equal to 7.
11. List the integer values that satisfy:
-4<3x+2\leq5
\begin{aligned} -4<3x&+2\leq5\\ -6<3&x\leq3\\ -2< \, &x\leq1 \end{aligned}
-2 is not included in the solution set as x is greater than -2.
1 is included in the solution set as x is less than or equal to 1.
Solving inequalities FAQs
Solving inequalities is where you calculate the values that an unknown variable can be in an inequality.
To solve an inequality, you need to balance the inequality on each side of the inequality sign in the same way as you would balance an equation on each side of the equal sign. Solutions can be integers, decimals, positive numbers, or negative numbers.
The next lessons are
- Types of graphs
- Math formulas
- Coordinate plane
Still stuck?
At Third Space Learning, we specialize in helping teachers and school leaders to provide personalized math support for more of their students through high-quality, online one-on-one math tutoring delivered by subject experts.
Each week, our tutors support thousands of students who are at risk of not meeting their grade-level expectations, and help accelerate their progress and boost their confidence.

Find out how we can help your students achieve success with our math tutoring programs .
[FREE] Common Core Practice Tests (Grades 3 to 6)
Prepare for math tests in your state with these Grade 3 to Grade 6 practice assessments for Common Core and state equivalents.
40 multiple choice questions and detailed answers to support test prep, created by US math experts covering a range of topics!
Privacy Overview
Solving Inequalities
Related Pages Solving Equations Algebraic Expressions More Algebra Lessons
In these lessons, we will look at the rules, approaches, and techniques for solving inequalities.
The following figure shows how to solve two-step inequalities. Scroll down the page for more examples and solutions.

The rules for solving inequalities are similar to those for solving linear equations. However, there is one exception when multiplying or dividing by a negative number.
To solve an inequality, we can:
- Add the same number to both sides.
- Subtract the same number from both sides.
- Multiply both sides by the same positive number.
- Divide both sides by the same positive number.
- Multiply both sides by the same negative number and reverse the sign.
- Divide both sides by the same negative number and reverse the sign.
Inequalities Of The Form “x + a > b” or “x + a < b”
Example: Solve x + 7 < 15
Solution: x + 7 < 15 x + 7 – 7 < 15 – 7 x < 8
Inequalities Of The Form “x – a < b” or “x – a > b”
Example: Solve x – 6 > 14
Solution: x – 6 > 14 x – 6+ 6 > 14 + 6 x > 20
Example: Solve the inequality x – 3 + 2 < 10
Solution: x – 3 + 2 < 10 x – 1 < 10 x – 1 + 1 < 10 + 1 x < 11
Inequalities Of The Form “a – x < b” or “a – x > b”
Example: Solve the inequality 7 – x < 9
Solution: 7 – x < 9 7 – x – 7 < 9 – 7 – x < 2 x > –2 (remember to reverse the symbol when multiplying by –1)
Example: Solve the inequality 12 > 18 – y
Solution: 12 > 18 – y 18 – y < 12 18 – y – 18 < 12 –18 – y < –6 y > 6 (remember to reverse the symbol when multiplying by –1)
Inequalities Of The Form “ < b” or “ > b”
Solving linear inequalities with like terms.
If an equation has like terms, we simplify the equation and then solve it. We do the same when solving inequalities with like terms.
Example: Evaluate 3x – 8 + 2x < 12
Solution: 3x – 8 + 2x < 12 3x + 2x < 12 + 8 5x < 20 x < 4
Example: Evaluate 6x – 8 > x + 7
Solution: 6x – 8 > x + 7 6x – x > 7 + 8 5x > 15 x > 3
Example: Evaluate 2(8 – p) ≤ 3(p + 7)
Solution: 2(8 – p) ≤ 3(p + 7) 16 – 2p ≤ 3p + 21 16 – 21 ≤ 3p + 2p –5 ≤ 5p –1 ≤ p p ≥ –1 (a < b is equivalent to b > a)
An Introduction To Solving Inequalities
Solving One-Step Linear Inequalities In One Variable
The solutions to linear inequalities can be expressed several ways: using inequalities, using a graph, or using interval notation.
The steps to solve linear inequalities are the same as linear equations, except if you multiply or divide by a negative when solving for the variable, you must reverse the inequality symbol.
Example: Solve. Express the solution as an inequality, graph and interval notation. x + 4 > 7 -2x > 8 x/-2 > -1 x - 9 ≥ -12 7x > -7 x - 9 ≤ -12
Solving Two-Step Linear Inequalities In One Variable
Example: Solve. Express the solution as an inequality, graph and interval notation. 3x + 4 ≥ 10 -2x - 1 > 9 10 ≥ -3x - 2 -8 > 5x + 12
Solving Linear Inequalities
Main rule to remember: If you multiply or divide by a negative number, the inequality flips direction.
Examples of how to solve linear inequalities are shown:
Example: Solve: 3x - 6 > 8x - 7
Students learn that when solving an inequality, such as -3x is less than 12, the goal is the same as when solving an equation: to get the variable by itself on one side.
Note that when multiplying or dividing both sides of an inequality by a negative number, the direction of the inequality sign must be switched.
For example, to solve -3x is less than 12, divide both sides by -3, to get x is greater than -4.
And when graphing an inequality on a number line, less than or greater than is shown with an open dot, and less than or equal to or greater than or equal to is shown with a closed dot.

We welcome your feedback, comments and questions about this site or page. Please submit your feedback or enquiries via our Feedback page.
- Inspiration
- Solve equations and inequalities
- Simplify expressions
- Factor polynomials
- Graph equations and inequalities
- Advanced solvers
- All solvers
- Arithmetics
- Determinant
- Percentages
- Scientific Notation
- Inequalities
Equations and Inequalities Involving Signed Numbers
In chapter 2 we established rules for solving equations using the numbers of arithmetic. Now that we have learned the operations on signed numbers, we will use those same rules to solve equations that involve negative numbers. We will also study techniques for solving and graphing inequalities having one unknown.
SOLVING EQUATIONS INVOLVING SIGNED NUMBERS
Upon completing this section you should be able to solve equations involving signed numbers.
Example 1 Solve for x and check: x + 5 = 3
Using the same procedures learned in chapter 2, we subtract 5 from each side of the equation obtaining
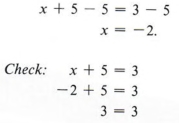
Example 2 Solve for x and check: - 3x = 12
Dividing each side by -3, we obtain
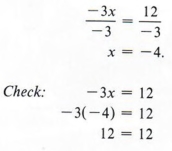

LITERAL EQUATIONS
- Identify a literal equation.
- Apply previously learned rules to solve literal equations.
An equation having more than one letter is sometimes called a literal equation . It is occasionally necessary to solve such an equation for one of the letters in terms of the others. The step-by-step procedure discussed and used in chapter 2 is still valid after any grouping symbols are removed.
Example 1 Solve for c: 3(x + c) - 4y = 2x - 5c
First remove parentheses.
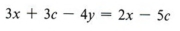
At this point we note that since we are solving for c, we want to obtain c on one side and all other terms on the other side of the equation. Thus we obtain
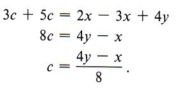
Sometimes the form of an answer can be changed. In this example we could multiply both numerator and denominator of the answer by (- l) (this does not change the value of the answer) and obtain
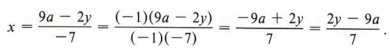
The advantage of this last expression over the first is that there are not so many negative signs in the answer.
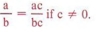
The most commonly used literal expressions are formulas from geometry, physics, business, electronics, and so forth.
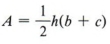
Notice in this example that r was left on the right side and thus the computation was simpler. We can rewrite the answer another way if we wish.
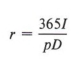
GRAPHING INEQUALITIES
- Use the inequality symbol to represent the relative positions of two numbers on the number line.
- Graph inequalities on the number line.
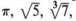
The symbols are inequality symbols or order relations and are used to show the relative sizes of the values of two numbers. We usually read the symbol as "greater than." For instance, a > b is read as "a is greater than b." Notice that we have stated that we usually read a < b as a is less than b. But this is only because we read from left to right. In other words, "a is less than b" is the same as saying "b is greater than a." Actually then, we have one symbol that is written two ways only for convenience of reading. One way to remember the meaning of the symbol is that the pointed end is toward the lesser of the two numbers.

In simpler words this definition states that a is less than b if we must add something to a to get b. Of course, the "something" must be positive.
If you think of the number line, you know that adding a positive number is equivalent to moving to the right on the number line. This gives rise to the following alternative definition, which may be easier to visualize.
Example 1 3 < 6, because 3 is to the left of 6 on the number line.

Example 2 - 4 < 0, because -4 is to the left of 0 on the number line.

Example 3 4 > - 2, because 4 is to the right of -2 on the number line.

Example 4 - 6 < - 2, because -6 is to the left of -2 on the number line.

The mathematical statement x < 3, read as "x is less than 3," indicates that the variable x can be any number less than (or to the left of) 3. Remember, we are considering the real numbers and not just integers, so do not think of the values of x for x < 3 as only 2, 1,0, - 1, and so on.
As a matter of fact, to name the number x that is the largest number less than 3 is an impossible task. It can be indicated on the number line, however. To do this we need a symbol to represent the meaning of a statement such as x < 3.
The symbols ( and ) used on the number line indicate that the endpoint is not included in the set.
Example 5 Graph x < 3 on the number line.

Note that the graph has an arrow indicating that the line continues without end to the left.
Example 6 Graph x > 4 on the number line.

Example 7 Graph x > -5 on the number line.

Example 8 Make a number line graph showing that x > - 1 and x < 5. (The word "and" means that both conditions must apply.)

Example 9 Graph - 3 < x < 3.

Example 10 x >; 4 indicates the number 4 and all real numbers to the right of 4 on the number line.
The symbols [ and ] used on the number line indicate that the endpoint is included in the set.

Example 13 Write an algebraic statement represented by the following graph.
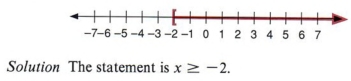
Example 14 Write an algebraic statement for the following graph.
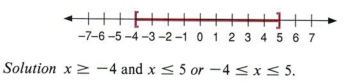
| -4 and 5. |
Example 15 Write an algebraic statement for the following graph.
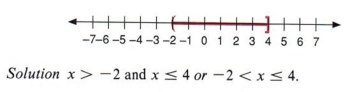
| -2. |
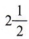
SOLVING INEQUALITIES
Upon completing this section you should be able to solve inequalities involving one unknown.
The solutions for inequalities generally involve the same basic rules as equations. There is one exception, which we will soon discover. The first rule, however, is similar to that used in solving equations.
If the same quantity is added to each side of an inequality , the results are unequal in the same order.
Example 1 If 5 < 8, then 5 + 2 < 8 + 2.
Example 2 If 7 < 10, then 7 - 3 < 10 - 3.
We can use this rule to solve certain inequalities.
Example 3 Solve for x: x + 6 < 10
If we add -6 to each side, we obtain
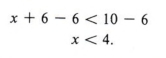
Graphing this solution on the number line, we have

We will now use the addition rule to illustrate an important concept concerning multiplication or division of inequalities.
Suppose x > a.
Now add - x to both sides by the addition rule.
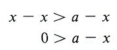
Now add -a to both sides.
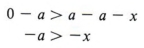
The last statement, - a > -x, can be rewritten as - x < -a. Therefore we can say, "If x > a, then - x < -a. This translates into the following rule:
If an inequality is multiplied or divided by a negative number, the results will be unequal in the opposite order.
Example 5 Solve for x and graph the solution: -2x>6
To obtain x on the left side we must divide each term by - 2. Notice that since we are dividing by a negative number, we must change the direction of the inequality.
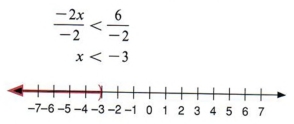
Take special note of this fact. Each time you divide or multiply by a negative number, you must change the direction of the inequality symbol. This is the only difference between solving equations and solving inequalities.
Once we have removed parentheses and have only individual terms in an expression, the procedure for finding a solution is almost like that in chapter 2.
Let us now review the step-by-step method from chapter 2 and note the difference when solving inequalities.
First Eliminate fractions by multiplying all terms by the least common denominator of all fractions. (No change when we are multiplying by a positive number.) Second Simplify by combining like terms on each side of the inequality. (No change) Third Add or subtract quantities to obtain the unknown on one side and the numbers on the other. (No change) Fourth Divide each term of the inequality by the coefficient of the unknown. If the coefficient is positive, the inequality will remain the same. If the coefficient is negative, the inequality will be reversed. (This is the important difference between equations and inequalities.)

- A literal equation is an equation involving more than one letter.
- The symbols are inequality symbols or order relations .
- a a is to the left of b on the real number line.
- To solve a literal equation for one letter in terms of the others follow the same steps as in chapter 2.
- To solve an inequality use the following steps: Step 1 Eliminate fractions by multiplying all terms by the least common denominator of all fractions. Step 2 Simplify by combining like terms on each side of the inequality. Step 3 Add or subtract quantities to obtain the unknown on one side and the numbers on the other. Step 4 Divide each term of the inequality by the coefficient of the unknown. If the coefficient is positive, the inequality will remain the same. If the coefficient is negative, the inequality will be reversed. Step 5 Check your answer.
Math Topics
More solvers.
- Add Fractions
- Simplify Fractions

Inequalities Practice Questions
Click here for questions, click here for answers, gcse revision cards.

5-a-day Workbooks

Primary Study Cards

Privacy Policy
Terms and Conditions
Corbettmaths © 2012 – 2024
If you're seeing this message, it means we're having trouble loading external resources on our website.
If you're behind a web filter, please make sure that the domains *.kastatic.org and *.kasandbox.org are unblocked.
To log in and use all the features of Khan Academy, please enable JavaScript in your browser.
Unit 5: Systems of linear equations and inequalities
About this unit.
If one line is useful, let's see what we can do with two lines. In this unit, we learn how to write systems of equations, solve those systems, and interpret what those solutions mean in a real-world contexts.
Introduction to systems of equations
- Systems of equations: trolls, tolls (1 of 2) (Opens a modal)
- Systems of equations: trolls, tolls (2 of 2) (Opens a modal)
- Testing a solution to a system of equations (Opens a modal)
- Systems of equations with graphing: y=7/5x-5 & y=3/5x-1 (Opens a modal)
- Systems of equations with graphing: exact & approximate solutions (Opens a modal)
- Solutions of systems of equations Get 3 of 4 questions to level up!
- Systems of equations with graphing Get 3 of 4 questions to level up!
Number of solutions to systems of equations
- Number of solutions to a system of equations (Opens a modal)
- Number of solutions to a system of equations graphically (Opens a modal)
- Number of solutions to a system of equations graphically Get 3 of 4 questions to level up!

Write a system of equations from a table or graph
- Intercepts from a table (Opens a modal)
- Calculating slope from tables (Opens a modal)
- Intercepts of lines review (x-intercepts and y-intercepts) (Opens a modal)
- Worked example: slope from graph (Opens a modal)
- Write systems of two linear equations given a table Get 3 of 4 questions to level up!
- Write systems of two linear equations given a graph Get 3 of 4 questions to level up!
Systems of equations from context
- Setting up a system of equations from context example (pet weights) (Opens a modal)
- Setting up a system of linear equations example (weight and price) (Opens a modal)
- Creating systems in context Get 3 of 4 questions to level up!
- Estimate graphically with systems of equations in real-world problems Get 3 of 4 questions to level up!
Interpreting points relative to a system of equations
- Interpreting points in context of graphs of systems (Opens a modal)
- Interpret points relative to a system Get 3 of 4 questions to level up!
Solving systems of equations with substitution
- Systems of equations with substitution: potato chips (Opens a modal)
- Systems of equations with substitution: -3x-4y=-2 & y=2x-5 (Opens a modal)
- Substitution method review (systems of equations) (Opens a modal)
- Systems of equations with substitution Get 3 of 4 questions to level up!
Solving systems of equations with elimination
- Systems of equations with elimination: King's cupcakes (Opens a modal)
- Elimination strategies (Opens a modal)
- Systems of equations with elimination: x-4y=-18 & -x+3y=11 (Opens a modal)
- Systems of equations with elimination: potato chips (Opens a modal)
- Systems of equations with elimination (and manipulation) (Opens a modal)
- Elimination method review (systems of linear equations) (Opens a modal)
- Combining equations Get 3 of 4 questions to level up!
- Elimination strategies Get 3 of 4 questions to level up!
- Systems of equations with elimination Get 3 of 4 questions to level up!
- Systems of equations with elimination challenge Get 3 of 4 questions to level up!
Equivalent systems of equations
- Why can we subtract one equation from the other in a system of equations? (Opens a modal)
- Worked example: equivalent systems of equations (Opens a modal)
- Worked example: non-equivalent systems of equations (Opens a modal)
- Reasoning with systems of equations (Opens a modal)
- Equivalent systems of equations review (Opens a modal)
- Reasoning with systems of equations Get 3 of 4 questions to level up!
Systems of equations word problems
- Age word problem: Imran (Opens a modal)
- Age word problem: Ben & William (Opens a modal)
- Age word problem: Arman & Diya (Opens a modal)
- System of equations word problem: walk & ride (Opens a modal)
- System of equations word problem: no solution (Opens a modal)
- System of equations word problem: infinite solutions (Opens a modal)
- Systems of equations with elimination: TV & DVD (Opens a modal)
- Systems of equations with elimination: apples and oranges (Opens a modal)
- Systems of equations with substitution: coins (Opens a modal)
- Systems of equations with elimination: coffee and croissants (Opens a modal)
- Systems of equations: FAQ (Opens a modal)
- Age word problems Get 3 of 4 questions to level up!
- Systems of equations word problems Get 3 of 4 questions to level up!
- Systems of equations word problems (with zero and infinite solutions) Get 3 of 4 questions to level up!
Graphing systems of two-variable inequalities
- Intro to graphing systems of inequalities (Opens a modal)
- Graphing systems of inequalities (Opens a modal)
- Systems of inequalities graphs Get 3 of 4 questions to level up!

- HW Guidelines
- Study Skills Quiz
- Find Local Tutors
- Demo MathHelp.com
- Join MathHelp.com
Select a Course Below
- ACCUPLACER Math
- Math Placement Test
- PRAXIS Math
- + more tests
- 5th Grade Math
- 6th Grade Math
- Pre-Algebra
- College Pre-Algebra
- Introductory Algebra
- Intermediate Algebra
- College Algebra
Examples of Solving Harder Linear Inequalities
Intro & Formatting Worked Examples Harder Examples & Word Prob's
Once you'd learned how to solve one-variable linear equations, you were then given word problems. To solve these problems, you'd have to figure out a linear equation that modelled the situation, and then you'd have to solve that equation to find the answer to the word problem.
Content Continues Below
MathHelp.com
Solving Inequalities
So, now that you know how to solve linear inequalities — you guessed it! — they give you word problems.
- The velocity of an object fired directly upward is given by V = 80 − 32 t , where the time t is measured in seconds. When will the velocity be between 32 and 64 feet per second (inclusive)?
This question is asking when the velocity, V , will be between two given values. So I'll take the expression for the velocity,, and put it between the two values they've given me. They've specified that the interval of velocities is inclusive, which means that the interval endpoints are included. Mathematically, this means that the inequality for this model will be an "or equal to" inequality. Because the solution is a bracket (that is, the solution is within an interval), I'll need to set up a three-part (that is, a compound) inequality.
I will set up the compound inequality, and then solve for the range of times t :
32 ≤ 80 − 32 t ≤ 64
32 − 80 ≤ 80 − 80 − 32 t ≤ 64 − 80
−48 ≤ −32 t ≤ −16
−48 / −32 ≥ −32 t / −32 ≥ −16 / −32
1.5 ≥ t ≥ 0.5
Note that, since I had to divide through by a negative, I had to flip the inequality signs.
Advertisement
Note also that you might (as I do) find the above answer to be more easily understood if it's written the other way around, with "less than" inequalities.
And, because this is a (sort of) real world problem, my working should show the fractions, but my answer should probably be converted to decimal form, because it's more natural to say "one and a half seconds" than it is to say "three-halves seconds". So I convert the last line above to the following:
0.5 ≤ t ≤ 1.5
Looking back at the original question, it did not ask for the value of the variable " t ", but asked for the times when the velocity was between certain values. So the actual answer is:
The velocity will be between 32 and 64 feet per second between 0.5 seconds after launch and 1.5 seconds after launch.
Okay; my answer above was *extremely* verbose and "complete"; you don't likely need to be so extreme. You can probably safely get away with saying something simpler like, "between 0.5 seconds and 1.5 seconds". Just make sure that you do indeed include the approprioate units (in this case, "seconds").
Always remember when doing word problems, that, once you've found the value for the variable, you need to go back and re-read the problem to make sure that you're answering the actual question. The inequality 0.5 ≤ t ≤ 1.5 did not answer the actual question regarding time. I had to interpret the inequality and express the values in terms of the original question.
- Solve 5 x + 7 < 3( x + 1) .
First I'll multiply through on the right-hand side, and then solve as usual:
5 x + 7 < 3( x + 1)
5 x + 7 < 3 x + 3
2 x + 7 < 3
2 x < −4
x < −2
In solving this inequality, I divided through by a positive 2 to get the final answer; as a result (that is, because I did *not* divide through by a minus), I didn't have to flip the inequality sign.
- You want to invest $30,000 . Part of this will be invested in a stable 5% -simple-interest account. The remainder will be "invested" in your father's business, and he says that he'll pay you back with 7% interest. Your father knows that you're making these investments in order to pay your child's college tuition with the interest income. What is the least you can "invest" with your father, and still (assuming he really pays you back) get at least $1900 in interest?
First, I have to set up equations for this. The interest formula for simple interest is I = Prt , where I is the interest, P is the beginning principal, r is the interest rate expressed as a decimal, and t is the time in years.
Since no time-frame is specified for this problem, I'll assume that t = 1 ; that is, I'll assume (hope) that he's promising to pay me at the end of one year. I'll let x be the amount that I'm going to "invest" with my father. Then the rest of my money, being however much is left after whatever I give to him, will be represented by "the total, less what I've already given him", so 30000 − x will be left to invest in the safe account.
Then the interest on the business investment, assuming that I get paid back, will be:
I = ( x )(0.07)(1) = 0.07 x
The interest on the safe investment will be:
(30 000 − x )(0.05)(1) = 1500 − 0.05 x
The total interest is the sum of what is earned on each of the two separate investments, so my expression for the total interest is:
0.07 x + (1500 − 0.05 x ) = 0.02 x + 1500
I need to get at least $1900 ; that is, the sum of the two investments' interest must be greater than, or at least equal to, $1,900 . This allows me to create my inequality:
0.02 x + 1500 ≥ 1900
0.02 x ≥ 400
x ≥ 20 000
That is, I will need to "invest" at least $20,000 with my father in order to get $1,900 in interest income. Since I want to give him as little money as possible, I will give him the minimum amount:
I will invest $20,000 at 7% .

- An alloy needs to contain between 46% copper and 50% copper. Find the least and greatest amounts of a 60% copper alloy that should be mixed with a 40% copper alloy in order to end up with thirty pounds of an alloy containing an allowable percentage of copper.
This is similar to a mixture word problem , except that this will involve inequality symbols rather than "equals" signs. I'll set it up the same way, though, starting with picking a variable for the unknown that I'm seeking. I will use x to stand for the pounds of 60% copper alloy that I need to use. Then 30 − x will be the number of pounds, out of total of thirty pounds needed, that will come from the 40% alloy.
Of course, I'll remember to convert the percentages to decimal form for doing the algebra.
| pounds | % copper | pounds copper | |
|---|---|---|---|
| 60% alloy | 0.6 | 0.6 | |
| 40% alloy | 30 − | 0.4 | 0.4(30 − ) = 12 − 0.4 |
| mixture | 30 | between 0.46 and 0.5 | between 13.8 and 15 |
How did I get those values in the bottom right-hand box? I multiplied the total number of pounds in the mixture ( 30 ) by the minimum and maximum percentages ( 46% and 50% , respectively). That is, I multiplied across the bottom row, just as I did in the " 60% alloy" row and the " 40% alloy" row, to get the right-hand column's value.
The total amount of copper in the mixture will be the sum of the copper contributed by each of the two alloys that are being put into the mixture. So I'll add the expressions for the amount of copper from each of the alloys, and place the expression for the total amount of copper in the mixture as being between the minimum and the maximum allowable amounts of copper:
13.8 ≤ 0.6 x + (12 − 0.4 x ) ≤ 15
13.8 ≤ 0.2 x + 12 ≤ 15
1.8 ≤ 0.2 x ≤ 3
9 ≤ x ≤ 15
Checking back to my set-up, I see that I chose my variable to stand for the number of pounds that I need to use of the 60% copper alloy. And they'd only asked me for this amount, so I can ignore the other alloy in my answer.
I will need to use between 9 and 15 pounds of the 60% alloy.
Per yoozh, I'm verbose in my answer. You can answer simply as " between 9 and 15 pounds ".
- Solve 3( x − 2) + 4 ≥ 2(2 x − 3)
First I'll multiply through and simplify; then I'll solve:
3( x − 2) + 4 ≥ 2(2 x − 3)
3 x − 6 + 4 ≥ 4 x − 6
3 x − 2 ≥ 4 x − 6
−2 ≥ x − 6 (*)
Why did I move the 3 x over to the right-hand side (to get to the line marked with a star), instead of moving the 4 x to the left-hand side? Because by moving the smaller term, I was able to avoid having a negative coefficient on the variable, and therefore I was able to avoid having to remember to flip the inequality when I divided through by that negative coefficient. I find it simpler to work this way; I make fewer errors. But it's just a matter of taste; you do what works for you.
Why did I switch the inequality in the last line and put the variable on the left? Because I'm more comfortable with inequalities when the answers are formatted this way. Again, it's only a matter of taste. The form of the answer in the previous line, 4 ≥ x , is perfectly acceptable.
As long as you remember to flip the inequality sign when you multiply or divide through by a negative, you shouldn't have any trouble with solving linear inequalities.
URL: https://www.purplemath.com/modules/ineqlin3.htm
Page 1 Page 2 Page 3
Standardized Test Prep
College math, homeschool math, share this page.
- Terms of Use
- Privacy / Cookies
- About Purplemath
- About the Author
- Tutoring from PM
- Advertising
- Linking to PM
- Site licencing
Visit Our Profiles
Solving Inequality Word Questions
(You might like to read Introduction to Inequalities and Solving Inequalities first.)
In Algebra we have "inequality" questions like:

Sam and Alex play in the same soccer team. Last Saturday Alex scored 3 more goals than Sam, but together they scored less than 9 goals. What are the possible number of goals Alex scored?
How do we solve them?
The trick is to break the solution into two parts:
Turn the English into Algebra.
Then use Algebra to solve.
Turning English into Algebra
To turn the English into Algebra it helps to:
- Read the whole thing first
- Do a sketch if needed
- Assign letters for the values
- Find or work out formulas
We should also write down what is actually being asked for , so we know where we are going and when we have arrived!
The best way to learn this is by example, so let's try our first example:
Assign Letters:
- the number of goals Alex scored: A
- the number of goals Sam scored: S
We know that Alex scored 3 more goals than Sam did, so: A = S + 3
And we know that together they scored less than 9 goals: S + A < 9
We are being asked for how many goals Alex might have scored: A
Sam scored less than 3 goals, which means that Sam could have scored 0, 1 or 2 goals.
Alex scored 3 more goals than Sam did, so Alex could have scored 3, 4, or 5 goals .
- When S = 0, then A = 3 and S + A = 3, and 3 < 9 is correct
- When S = 1, then A = 4 and S + A = 5, and 5 < 9 is correct
- When S = 2, then A = 5 and S + A = 7, and 7 < 9 is correct
- (But when S = 3, then A = 6 and S + A = 9, and 9 < 9 is incorrect)
Lots More Examples!

Example: Of 8 pups, there are more girls than boys. How many girl pups could there be?
- the number of girls: g
- the number of boys: b
We know that there are 8 pups, so: g + b = 8, which can be rearranged to
We also know there are more girls than boys, so:
We are being asked for the number of girl pups: g
So there could be 5, 6, 7 or 8 girl pups.
Could there be 8 girl pups? Then there would be no boys at all, and the question isn't clear on that point (sometimes questions are like that).
- When g = 8, then b = 0 and g > b is correct (but is b = 0 allowed?)
- When g = 7, then b = 1 and g > b is correct
- When g = 6, then b = 2 and g > b is correct
- When g = 5, then b = 3 and g > b is correct
- (But if g = 4, then b = 4 and g > b is incorrect)
A speedy example:

Example: Joe enters a race where he has to cycle and run. He cycles a distance of 25 km, and then runs for 20 km. His average running speed is half of his average cycling speed. Joe completes the race in less than 2½ hours, what can we say about his average speeds?
- Average running speed: s
- So average cycling speed: 2s
- Speed = Distance Time
- Which can be rearranged to: Time = Distance Speed
We are being asked for his average speeds: s and 2s
The race is divided into two parts:
- Distance = 25 km
- Average speed = 2s km/h
- So Time = Distance Average Speed = 25 2s hours
- Distance = 20 km
- Average speed = s km/h
- So Time = Distance Average Speed = 20 s hours
Joe completes the race in less than 2½ hours
- The total time < 2½
- 25 2s + 20 s < 2½
So his average speed running is greater than 13 km/h and his average speed cycling is greater than 26 km/h
In this example we get to use two inequalities at once:

Example: The velocity v m/s of a ball thrown directly up in the air is given by v = 20 − 10t , where t is the time in seconds. At what times will the velocity be between 10 m/s and 15 m/s?
- velocity in m/s: v
- the time in seconds: t
- v = 20 − 10t
We are being asked for the time t when v is between 5 and 15 m/s:
So the velocity is between 10 m/s and 15 m/s between 0.5 and 1 second after.
And a reasonably hard example to finish with:
Example: A rectangular room fits at least 7 tables that each have 1 square meter of surface area. The perimeter of the room is 16 m. What could the width and length of the room be?
Make a sketch: we don't know the size of the tables, only their area, they may fit perfectly or not!
- the length of the room: L
- the width of the room: W
The formula for the perimeter is 2(W + L) , and we know it is 16 m
- 2(W + L) = 16
- L = 8 − W
We also know the area of a rectangle is the width times the length: Area = W × L
And the area must be greater than or equal to 7:
- W × L ≥ 7
We are being asked for the possible values of W and L
Let's solve:
So the width must be between 1 m and 7 m (inclusive) and the length is 8−width .
- Say W = 1, then L = 8−1 = 7, and A = 1 x 7 = 7 m 2 (fits exactly 7 tables)
- Say W = 0.9 (less than 1), then L = 7.1, and A = 0.9 x 7.1 = 6.39 m 2 (7 won't fit)
- Say W = 1.1 (just above 1), then L = 6.9, and A = 1.1 x 6.9 = 7.59 m 2 (7 fit easily)
- Likewise for W around 7 m
- School Guide
- Mathematics
- Number System and Arithmetic
- Trigonometry
- Probability
- Mensuration
- Maths Formulas
- Class 8 Maths Notes
- Class 9 Maths Notes
- Class 10 Maths Notes
- Class 11 Maths Notes
- Class 12 Maths Notes
Solving Inequalities Practice Questions
Inequalities are fundamental in mathematics and are used extensively in various branches such as algebra, calculus, optimization and more. They describe relationships between variables and constants and are essential in solving problems involving ranges of values, constraints and conditions.
Solving inequalities often involves manipulating expressions algebraically, graphing on number lines or coordinate planes and understanding intervals of possible solutions. The solutions to inequalities are sets of values or intervals that satisfy the given inequality condition.
What is Inequality?
In mathematics, an inequality is a statement that compares two expressions or values, indicating their relative sizes. Unlike equations, which assert equality between two expressions, inequalities express a relationship where one expression is greater than, less than, greater than or equal to, or less than or equal to another expression.
Example : 2x + 5 < 1 = This inequality states that 2 times some unknown number x, plus 5, is strictly less than 1.
Unlike equations where both sides aim to be equal, inequalities establish a relationship between expressions using symbols like:
- < (less than)
- > (greater than)
- ≤ (less than or equal to)
- ≥ (greater than or equal to)
Formally, an inequality is typically written in one of the following forms:
| Inequality Name | Symbol | Expression | Description |
|---|---|---|---|
| Greater than | > | x a | x is greater than a |
| Less than | < | x a | x is less than a |
| Greater than equal to |
| x a | x is greater than or equal to a |
| Less than equal to |
| x a | x is less than or equal to a |
| Not equal |
| x a | x is not equal to a |
Question 1: Linear Inequality : Solve the inequality: 3x+5>11
3x+5>11 Subtract 5 from both sides: 3x>6 Divide both sides by 3: x>2 So, the solution is x>2
Question 2: Compound Inequality : Solve the compound inequality: -2<2x+3≤7
Break it into two parts: -2<2x+3 and 2x+3 ≤ 7 -2<2x+3 Subtract 3 from all parts: -5<2x Divide by 2: -5/2 <x 2x+3 ≤ 7 Subtract 3 from all parts: 2x ≤ 4 Divide by 2: x ≤2 So, the solution to -2 < 2x+3 ≤ 7 is -5/2 <x ≤2
Question 3: Absolute Value Inequality : Solve the inequality: ∣x-3∣≥4
Consider two cases: (i) x-3≥4 Add 3 to both sides: x ≥ 7 (ii) x-3≤-4 Add 3 to both sides: x ≤ -1 So, the solution to ∣x-3∣ ≥ 4 is x≤-1 or x ≥7
Question 4: Quadratic Inequality : Solve the inequality: x 2 -4x<3
Rewrite it as: x 2 -4x-3<0 Factorize the quadratic expression: (x-3)(x+1)<0 Analyze the sign changes: The inequality holds when -1<x<3 So, the solution to x 2 – 4x <3 is -1 < x < 3
Question 5: Rational Inequality: Solve the inequality: (x-2) / (x+1) > 0
Consider where the numerator and denominator change signs:
- Numerator (x-2) changes sign at x = 2
- Denominator (x+1) changes sign at x = -1
Test intervals:
- For x<-1 or -1 <x<2, (x-2) / (x+1) <0
- For x > 2 or -1 < x < 2, (x-2) / (x+1) >0
So, the solution for (x-2)/(x+1) > 0 is x <-1 or x> 2
Question 6: Exponential Inequality : Solve the inequality: 2 x – 1 < 8
Rewrite 8 as a power of 2: 2 x – 1 < 2 3 Since the bases are the same, equate the exponents: x-1 < 3 Add 1 to both sides: x < 4 So, the solution to 2 x – 1 < 8 is x < 4
Question 7: Logarithmic Inequality : Solve the inequality: log(x+1)>log(4)
Since the logarithm function is increasing: log(x+1) > log(4) x + 1 > 4 Subtract 1 from both sides: x > 3 So, the solution to log(x+1) > log(4) is x > 3
Question 8: Polynomial Inequality: Solve the polynomial inequality: x 3 – 2x 2 – 3x > 0
Factorize the polynomial (if possible) or analyze intervals: x 3 – 2x 2 – 3x > 0 x(x-3)(x+1) > 0 Determine sign changes and intervals: Inequality holds when x < -1 or x > 3 So , the solution for x 3 – 2x 2 – 3x > 0 is x <-1 or x > 3
Question 9: Solve the compound inequality: 1 < 2x + 3 < 7
Split this into two separate inequalities: 1 < 2x+3 and 2x+3 < 7 Solve the first inequality: 1 < 2x + 3 Subtract 3 from both sides: -2 < 2x Divide both sides by 2: -1 < x Solve the second inequality 2x+3 < 7 Subtract 3 from both sides: 2x < 4 Divide both sides by 2: x < 2 So, the solution set for the compound inequality 1 < 2x+3 < 7 is -1 < x < 2
Question 10: Solve an inequality with absolute values: Solve ∣3x+2∣<7
Consider two cases for the absolute value inequality: Case 1: 3x+2 < 7 3x < 5 x < 5/3 Case 2: -(3x+2) < 7 -3x-2 < 7 Subtract 2 from both sides: -3x < 9 Divide both sides by -3 (flip the inequality sign): x > -3 Combining the solutions from both cases, we get -3 < x < 5/3
Triangle Inequality theorem Linear Inequalities Compound Inequalities
Solving Inequalities – FAQs
What is concept of inequality in maths.
Inequalities are the mathematical expressions in which both sides are not equal. In inequality, unlike in equations, we compare two values. The equal sign in between is replaced by less than (or less than or equal to), greater than (or greater than or equal to), or not equal to sign.
What is the Most Important thing to Remember when Solving Inequalities?
If you multiply or divide both sides of an inequality by the same positive number, the inequality remains true. But if you multiply or divide both sides of an inequality by a negative number, the inequality is no longer true. In fact, the inequality becomes reversed.
What is Difference Between an Equation and an Inequality?
Equations and inequalities are both mathematical sentences formed by relating two expressions to each other. In an equation, the two expressions are deemed equal which is shown by the symbol =. Where as in an inequality, the two expressions are not necessarily equal which is indicated by the symbols: >, <, ≤ or ≥.
What is Theorem of Inequality?
According to triangle inequality theorem, for any given triangle, the sum of two sides of a triangle is always greater than the third side. A polygon bounded by three line-segments is known as the Triangle.

Please Login to comment...
Similar reads.
- Arithmetic - MAQ
- Practice Questions
- School Learning
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
6-7 skills practice solving radical equations and inequalities
There are different types of math problems . An example of radical equations and inequalities practice question is [tex]\sqrt{x}[/tex] = 5
The term radical inequality is known to be a form of an inequality that maintains a variable expression that is present within it.
For the above question , find the [tex]\sqrt{x}[/tex] = 5
The next step is to square both side:
When you square both side, it will be
Learn more about radical inequality from
https://brainly.com/question/25243740
Related Questions
What is the value of x? sin64°=cosx enter your answer in the box. x = °
Sin and cosine of the acute angle are complementary trigonometric functions. This means that between these trigonometric functions, the rule of complementary acute angles applies: sin64° = cos(90°-64°) = cos26°
So, if we have given cos64° = cosx and we want to determine the value of the acute angle x, given the complementarity of the angles to 90 degrees, the required value of the angle x is 26°.
The answer is: x = 26°
When describing electromagnetic radiation, there is a(n) _____________ relationship between wavelength and frequency and the greater the frequency, the ____________ energy the electromagnetic radiation has
an should be there isn't it
a student wants to determine whether a certain problem is undecidable. which of the following will demonstrate that the problem is undecidable?
A scenario which demonstrate that the problem is undecidable is when for an instance of the problem , no algorithm written provides a correct YES or NO answer .
An algorithm can be defined as a standard formula and procedures with a set of finite steps and instructions that are executed on a computer system, in order to proffer solutions to a specific problem under appropriate conditions.
This ultimately implies that, a scenario which demonstrate that a certain problem is undecidable is when for an instance of the problem , no algorithm can be written by a programmer is capable of providing either a correct YES or NO answer .
Read more on algorithm here: brainly.com/question/24793921
According to the video, what are the purposes of the dodd-frank act? check all that apply
where's the video?
Explanation:
where da video at gang?????
You are high up in the mountains and boil water to make some tea. however, when you drink your tea, it is not as hot as it should be. you try again and again, but the water is just not hot enough to make a hot cup of tea. which is the best explanation for this result?
temperatures are all low on topbof the mountains
Answer:the cold
Explanation:mountains have this thing called an ice cap at the top
4. 1 1 describe two ways how social media platforms are abused
Hi, here are the ways social media platform are abused:
Hope this helps! Please correct me if I am wrong.
Which of these is not a reason for percent yield to be less than theoretical yield?
Answer:>incomplete reactions, in which some of the reactants do not react to form the product
practical losses during the experiment
->side reactions (unwanted reactions that compete with the desired reaction)
->reversible reactions
->impurities in reactants
not a reason? if you ask a reason ,i can say An actual yield is the mass of a product actually obtained from the reaction. It is usually less than the theoretical yield. The reasons for this include:
In the interview, dr. Dowell mentions that we live in a "small world. " the video explains that disease can spread in a matter of hours when people travel by airplane. How does the video connect to what dr. Dowell says? the video discusses disease but avoids how diseases spread. The video gives the same information as the interview about the spread of disease. The video gives less information than the interview about how easily disease can spread. The video gives more specific information about how easily diseases can spread
the answer is right all you have to do is trust me
Chord ac intersects chord bd at point p in circle z. ap=4 cm bp=5 cm pc=8 cm what is pd? enter your answer as a decimal in the box.
For this question, PD = 6.4 cm
Suppose a five-year, bond with annual coupons has a price of and a yield to maturity of . what is the bond's coupon rate?
The bond's coupon rate with an annual coupon that has a price of $903.35 and the yield to maturity will be 3.33%.
It should be noted that the formula for calculating the coupon rate is given as:
= Annual coupon / Face value
From the complete question, the annual coupon is $33.30 and the face value is $1000. Therefore, the coupon rate will be:
= 33.30/1000
Learn more about coupon rate on:
https://brainly.com/question/7459025
Rebello's preferred stock pays a dividend of $1.00 per quarter, and it sells for $55.00 per share. what is its effective annual (not nominal) rate of return?
Assuming it sells for $55.00 per share. Its effective annual (not nominal) rate of return is 7.47%.
Using this formula
Effective annual rate of return=[1+(Preferred quarterly dividend+Preferred stock price]^Periods per year-1
Periods per year = 4
Preferred quarterly dividend= $1.00
Preferred stock price= $55.00
Let plug in the formula
Effective annual rate of return = [1+ ($1.00/$55.00)]^4 - 1
Effective annual rate of return=(1+0.018181818)^4-1
Effective annual rate of return=(1.018181818)^4-1
Effective annual rate of return =1.0747-1
Effective annual rate of return =0.0747×100
Effective annual rate of return = 7.47%
Therefore the Effective annual rate of return will be 7.47%.
Learn more about effective rate of return here:https://brainly.com/question/15728540
You are given some ferrous iodide, fei2 , and are asked to extract the iron through electrolysis. what can be said about the merits of molten versus aqueous fei2 ?
It is impossible to extract or derive iron metal from the electrolysis of the aqueous solution provided. The option left is to carry out the electrolysis on the molten salt.
Electrolysis refers to the process of causing a chemical decomposition in a liquid or solution that contains ions by sending electric currents via such a solution.
Electrolysis is used primarily for:
Learn more about Electrolysis at : https://brainly.com/question/12054569
Bill was injured on the job and hospitalized for several months
WHAT HAPPENED TO BILL AFTER THAT???
Fungi are __________, whereas plants are autotrophs
Heterotrophs
fungi heterotrophs which means they cannot make their own food, where as plants are autotrops .
What effects can apostrophe have on a poem? choose four answers. It gives the speaker a voice. It connects the reader to the speaker’s message. It gives the poem a detached effect. It makes an imagined addressee feel present. It gives the poem a personalized effect
Th influence of apostrophe's as used on the poem is:
An apostrophe is known to be often used to highlight the vital reasons of the the main idea or object.
It is often used to adds drama , bring out emotions as a result of jubilation to sorrow and it is also used to evoke something not living.
Learn more about this poem from
https://brainly.com/question/12659789
A - it gives the speaker a voice
B - it connects the reader to the speakers message
D - it makes an imagined addressee feel present
E - it gives the poem a personalized effect
Go math grade 8 practice and skills fluency workbook answer key
the answer should be on a quizlet that i found
Go Math Middle School Grade 8, Practice Fluency Workbook
1st Edition
HOUGHTON MIFFLIN HARCOURT
here is the edition you need
hope this helps
rate brainliest
genes, which contain trait specifying information, are located on ______.
Chromosomes is a gene that contain trait specifying information. I don't know if this will help or not.
Suppose the microwave’s power is 900w (1watt=1joule/sec). how long would you have to heat the coffee in part a?
The amount of time that is required for the microwave to heat the coffee is 34.4 seconds .
Given the following data:
In order to determine the amount of time that is required for the microwave to heat the coffee, we would use this formula :
[tex]Energy = power \times time\\\\[/tex]
Making time the subject of formula , we have:
[tex]Time = \frac{Energy}{Power}[/tex]
Substituting the given parameters into the formula , we have;
[tex]Time = \frac{30962}{900}[/tex]
Time = 34.4 seconds .
Read more on time here: https://brainly.com/question/16894694
Course 1 chapter 10 volume and surface area answer key
An example of Course 1 chapter 10 volume and surface area question is find the volume of the figure (image attached.) The volume is option C.
Surface area is a term that connote the total area which the surface of the object is said to occupy. It is often divided into a sum of base area(s) and also lateral surface area.
To solve for the volume,
v 7.2 (3.2) (5.2)
Therefore , v = 125.528m³
Learn more about surface area from
https://brainly.com/question/16519513
Suppose that the rabbit population on mr. jenkins' farm follows the formula
Jenkins' farm tracks the procedure p(t)=3000tt+1. where t≥0 is the period (in months) since the start of the year.
As time (t) increases, the rabbit population (p(t)) will also increase , but it will approach a maximum value without ever actually reaching it, resulting in continuous growth that slows down over time.
Given formula: p(t) = 300t / (t + 1)
As time (t) increases , the denominator (t + 1) also increases .
The rabbit population (p(t)) is calculated by dividing 300t by (t + 1).
Now, let's examine the behaviour as t becomes larger:
When t is very small (close to 0), the population p(t) is also small, since the denominator (t + 1) is close to 1.
As t increases, the denominator (t + 1) grows, causing the value of p(t) to increase.
However, the rate of increase slows down as t gets larger.
This is because the denominator grows faster than the numerator (300t).
Eventually , as t becomes very large, the value of p(t) approaches but never quite reaches a maximum value.
This behaviour is characteristic of a rational function where the numerator's growth is outpaced by the denominator's growth, resulting in an asymptotic approach to a certain value.
Learn more about functions here:
https://brainly.com/question/28533782
The complete question:
Population Growth Suppose that the rabbit population on Mr. Jenkins’ farm follows the formula p(t) = 300t / (t + 1)
where t ≥ 0 is the time in months since the beginning of the year.
(a) Draw a graph of the rabbit population.
(b) What eventually happens to the rabbit populations.
Complete the following statements with the best answer. when one is using the standard normal distribution. p(z < 0) = ___________.
In Statistics, when you are is using the standard normal distribution , P( z < 0 ) = 0.5.
A normal distribution is also referred to as the Gaussian distribution and it can be defined as a probability distribution that is continuous and symmetrical on both sides of the mean , which shows that all data near the mean have a higher frequency than data that are far from the mean .
This ultimately implies that, when you are is using the standard normal distribution , P( z < 0 ) must be equal to 0.5 because it has a median of zero ( 0 ).
Read more on normal distribution here: https://brainly.com/question/4637344
A large industrial machine is able to monitor brainly
yes, they just monitor by flagged key words.
I run a book club with $n$ people, not including myself. every day, for $365$ days, i invite three members in the club to review a book. what is the smallest positive integer $n$ so that i can avoid ever having the exact same group of three members over all $365$ days?
The smallest positive integer n so that you can avoid ever having the exact same group of three members over all 365 days is; 11
if we have n people and we want to do groups of 5, the total number of different combinations is:
ⁿC₅ = n!/((n - 5)!5!)
By using the Brute force method, we have;
Now, If n = 9,
C = 9!/((9 - 5)!5!)
We want to find the smallest n such that c > 365. Thus, C = 126 is too small.
Let's try n = 11;
C = 11!/(6! * 5!) = 462
This is greater than 365 and so we need at least 11 members in the club.
Read more about Probability combination at; https://brainly.com/question/16830773
Among all pairs of numbers whose difference is 14 find a pair whose product is as small as possible
The pair two numbers whose difference is 14 and the product is as small as possible (i.e. -49) are (-7,7)
In mathematical concepts, word problems involve a crucial understanding of the problem and knowing which mathematical method and arithmetic operations are best suited to solving the problem.
If we assume that the smaller number should be = a and the larger number = a + 14.
Thus, their product (X) can be expressed as:
The smallest possible value implies the minimum value , i.e.
[tex]\mathbf{\dfrac{dX}{da} = 2a + 14}[/tex]
2a + 14 = 0
Therefore, we can conclude that the pair of two numbers whose difference is 14 and the product is as small as possible (i.e. -49) is (-7,7).
Learn more about word problems here:
https://brainly.com/question/21405634
Choose the best spanish equivalent to the phrase. El profesor termina su ____ (4th) año de estudios. Novena quinto cuarto segundo
El profesor termina su cuarto año de estudios.
The teacher finishes his fourth (4th) year of studies . So, the correct option is C .
Study is the act of learning something new or gaining knowledge through instruction, research, or reading. It usually entails making a concentrated and deliberate effort to comprehend and retain knowledge , frequently with the aim of reaching a certain academic or professional conclusion.
There are several ways to learn, including reading, making notes, watching lectures, practicing using exercises or issues, and participating in group projects or discussions. Although it is frequently connected to formal education, it can also be done privately or informally and is a crucial aspect of the learning process.
Studying is crucial for personal skill development in addition to educational advancement. Your confidence, skill, and self-esteem can all be increased by having effective study techniques. Additionally, it aids in lowering tension and worry related to tests and deadlines .
So, the correct option is C .
Learn more about Study , here:
https://brainly.com/question/30701980
Your question is in Spanish, but the English translation is most likely:
Choose the best Spanish equivalent to the phrase. The teacher finishes his ____ (4th) year of studies.
Six performers are to present their musical numbers in an auditorium. one of the performers requested to be the last act. in how many ways can the performances be arranged if the request was granted?
The numbers of ways that the performances can be arranged if the request was granted is 1 20 ways.
The term performance is a term that can be countable or uncountable in nature. Note that to calculate the performance, since it is 6, one has to times from 5 to 1:
5*4*3*2*1=20*6=120
So, the request can be granted is 120 ways.
Learn more about performances from
https://brainly.com/question/1532968
with the exception of one or two news stations, there is not much credible evidence that any particular mainstream news source is explicitly biased in one direction or the other in terms of its news coverage.
There is credible evidence that mainstream news source is explicitly biased in one direction or the other in terms of its news coverage is a true statement.
Research has shown that there is overriding bias in the news where it goes to one direction of stories with the aim of getting the largest audience .
Note that media bias is said to be a deliberate or unintentional bending of news reporting toward one direction as a result of political views, etc.
Learn more about bias from
https://brainly.com/question/24491228
In paragraphs 19 and 20 of this story, the man reflects back on his own father cooking for him, and he recalls one incident in particular that he feels bad about. Write a story about this incident, told in first person by the man’s father. Use details from the paragraphs, and add elaboration of your own to show the father’s feelings about what happened and how he reacted to it
People often write story about different incident. The story is given below.
The incident is a story that revolve around our character which I named Olu . He was an man who loved to make food for his son. His feel is immersed in all his love but Chide his son did not reciprocate his love.
The father was said about his child who did not look at the meal he has prepared for him. He was sick and dying and that was the only thing he could do for him. He knows he loves his son and his son loves him too, but this character of his displeased him but still he accepted and move on.
Learn more about feelings from
https://brainly.com/question/14370337
Big ideas math geometry chapter 9 practice test answers
A book has a mass of 400g the surface of the book in contact
The pressure exerted on the table due to the book is 200 N/m².
The given parameters;
mass of the book, m = 400 g = 0.4 kg
dimension of the table, = 0.10m x 0.20 m.
gravitational field strength g = 10 N/kg.
The area of the table is calculated as follows;
A = 0.1 x 0.2 = 0.02 m²
The pressure exerted on the table due to the book is calculated as follows; where;
F is the force of the book due to its weight
Thus, the pressure exerted on the table due to the book is 200 N/m².
Calculate for all schools
Your chance of acceptance, your chancing factors, extracurriculars, breaking down the sat: what type of math is on it.
As I'm studying for the SAT, I realize that there are different types of math problems in my review. Can anyone let me know what type of math is typically tested on the SAT?
Of course! The math on the SAT covers several areas, and is divided into two sections. Here's a basic breakdown:
1. Heart of Algebra: This includes linear equations and systems. This section is all about analyzing and solving problems involving linear relationships. This means you'll be dealing with mathematical expressions, linear equations, linear inequalities, and linear functions.
2. Problem Solving and Data Analysis: This is about being quantitatively literate. This includes ratios, rates, proportional relationships, and scaling. You will also deal with statistics where you have to analyze, represent, and interpret data. It's also worth mentioning that you'll encounter questions based on basic probability.
3. Passport to Advanced Math: This section delves into the more complex equations and functions. Essentially, you'll be dealing with quadratic and exponential functions. Basically, these are expressions and equations which involve the manipulation of complex equations.
4. Additional Topics in Math: This encompasses several other areas like geometry and trigonometry. You'll see questions on volumes of solids, triangle properties, circle properties, radians, and the Pythagorean theorem.
Important to note: as of 2024, when the SAT became completely digital, you can use your calculator on both of the math modules. This should come in handy especially when dealing with complex equations or larger numbers.
Keep working hard on your practicing. Your diligence will pay off in the end! Good luck.
About CollegeVine’s Expert FAQ
CollegeVine’s Q&A seeks to offer informed perspectives on commonly asked admissions questions. Every answer is refined and validated by our team of admissions experts to ensure it resonates with trusted knowledge in the field.

- Advanced Search
Numerical analysis of a variational-hemivariational inequality governed by the Stokes equations
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, view options, recommendations, on numerical approximation of a variational–hemivariational inequality modeling contact problems for locking materials.
This paper is devoted to numerical analysis of a new class of elliptic variational–hemivariational inequalities in the study of a family of contact problems for elastic ideally locking materials. The contact is described by the ...
A new local stabilized nonconforming finite element method for solving stationary Navier-Stokes equations
In this paper we study a new local stabilized nonconforming finite element method based on two local Gauss integrals for solving the stationary Navier-Stokes equations. This nonconforming method utilizes the lowest equal-order pair of mixed finite ...
Mixed Finite Element Method for a Hemivariational Inequality of Stationary Navier–Stokes Equations
In this paper, we develop and study the mixed finite element method for a hemivariational inequality of the stationary Navier–Stokes equations (NS hemivariational inequality). The NS hemivariational inequality models the motion of a viscous ...
Information
Published in.
Pergamon Press, Inc.
United States
Publication History
Author tags.
- Variational-hemivariational inequality
- Stokes problem
- Leak and slip condition
- Mixed finite element method
- Error estimate
- Research-article
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 0 Total Downloads
- Downloads (Last 12 months) 0
- Downloads (Last 6 weeks) 0
View options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
Share this publication link.
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.
Anthropic CEO says we need to think bigger than a universal basic income if we want to solve the AI inequality problem
- Some fear that rapid advances in AI may concentrate power and wealth among a small elite.
- Anthropic CEO Dario Amodei says a universal basic income may not sufficiently address such a shift.
- He says there needs to be a broader economic reorganization.

The rapid advances in AI could consolidate power and wealth in the hands of a small few , which is why many in the tech industry have called for a universal basic income.
But some AI leaders say even UBI, a recurring cash payment to those in a given population regardless of their wealth or employment status, wouldn't be enough.
"I certainly think that's better than nothing," Anthropic CEO Dario Amodei told Time. "But I would much prefer a world in which everyone can contribute. It would be kind of dystopian if there are these few people that can make trillions of dollars, and then the government hands it all out to the unwashed masses."
Amodei, a former OpenAI employee, launched Anthropic in 2021 with his sister, Daniela, and five other OpenAI colleagues. They believed AI would have a dramatic impact on the world and wanted to build a company that would ensure it was aligned with human values. Amodei described the company to Time as one focused on "public benefit."
Many in the tech industry have expressed support for universal basic income to mitigate the economic impact of AI. The idea is that it would act as a safety net for people whose jobs have been threatened by the technology.
But Amodei suggests that AI will alter society in such a fundamental way that we need to design a more comprehensive solution. "I think in the long run, we're really going to need to think about how do we organize the economy and how humans think about their lives?" He doesn't have the answer, he said, in part because he believes it needs to be a "conversation among humanity."
Amodei isn't the only one thinking beyond universal basic income. OpenAI CEO Sam Altman, while a vocal proponent of it, has also proposed the idea of a " universal basic compute ." The idea is that as large language models advance, owning a slice of one will be more valuable than money.
Watch: Why "deployment of AI is top of mind for everybody," according to IBM's Jonathan Adashek
- Main content

VIDEO
COMMENTS
Unit test. Level up on all the skills in this unit and collect up to 1,100 Mastery points! There are lots of strategies we can use to solve equations. Let's explore some different ways to solve equations and inequalities. We'll also see what it takes for an equation to have no solution, or infinite solutions.
Summary. Many simple inequalities can be solved by adding, subtracting, multiplying or dividing both sides until you are left with the variable on its own. But these things will change direction of the inequality: Multiplying or dividing both sides by a negative number. Swapping left and right hand sides.
3x/3 < 18/3. x < 6. Solving this example required two steps (step one: subtract 8 from both sides; step two: divide both sides by 3). The result is the solved inequality x<6. The step-by-step procedure to solving example #2 is illustrated in Figure 04 below. Figure 04: How to solve an inequality: 3x+8<26.
One-step inequalities: -5c ≤ 15. (Opens a modal) One-step inequality involving addition. (Opens a modal) One-step inequality word problem. (Opens a modal) Inequalities using addition and subtraction. (Opens a modal) Solving and graphing linear inequalities.
Linear equations and inequalities: Unit test; About this unit. ... Two-step inequality word problems Get 3 of 4 questions to level up! Multi-step inequalities. Learn. Inequalities with variables on both sides (Opens a modal) ... Solving proportions Get 5 of 7 questions to level up!
Answer. Inequality: x < −3 x < − 3. Interval: (−∞, −3) ( − ∞, − 3) Graph: −2 − 2, the inequality symbol was switched from > to <. [/hidden-answer] The following video shows examples of solving one step inequalities using the multiplication property of equality where the variable is on the left hand side.
Solving inequalities is similar to solving equations, but where an equation has one unique solution, an inequality has a range of solutions. ... Solve word problems leading to inequalities of the form px + q > r or px + q < r, where p, q, and r are specific rational numbers. Graph the solution set of the inequality and interpret it in the ...
The steps to solve linear inequalities are the same as linear equations, except if you multiply or divide by a negative when solving for the variable, you must reverse the inequality symbol. Example: Solve. Express the solution as an inequality, graph and interval notation. x + 4 > 7.
Follow these simple steps to solve inequalities! Walk through this free, interactive lesson to master this essential algebra skill. Start learning!
Step 4 Divide each term of the inequality by the coefficient of the unknown. If the coefficient is positive, the inequality will remain the same. If the coefficient is negative, the inequality will be reversed. Step 5 Check your answer. Solve linear or quadratic inequalities with our free step-by-step algebra calculator.
inequality. Practice Questions. Previous: Graphical Inequalities Practice Questions. Next: Cumulative Frequency and Box Plot Practice Questions. The Corbettmaths Practice Questions on inequalities.
Using inequalities to solve problems. Sergei runs a bakery. He needs at least 175 kilograms of flour in total to complete the holiday orders he's received. He only has 34 kilograms of flour, so he needs to buy more. The flour he likes comes in bags that each contain 23 kilograms of flour. He wants to buy the smallest number of bags as possible ...
This page titled 6.E: Solving Equations and Inequalities (Exercises) is shared under a CC BY-NC-SA 3.0 license and was authored, remixed, and/or curated by Anonymous via source content that was edited to the style and standards of the LibreTexts platform.
In this unit, we learn how to write systems of equations, solve those systems, and interpret what those solutions mean in a real-world contexts. If you're seeing this message, it means we're having trouble loading external resources on our website. ... Systems of linear equations and inequalities: Quiz 1; ... Systems of equations word problems ...
The form of the answer in the previous line, 4 ≥ x, is perfectly acceptable. As long as you remember to flip the inequality sign when you multiply or divide through by a negative, you shouldn't have any trouble with solving linear inequalities. Page 1 Page 2. Page 3. Linear inequalities can be simple (x<3) or complex (3x+2≤½−14x), and ...
Isolate the variable by subtracting 3 from both sides of the inequality. x < 2. The graph of the inequality x < 2 is shown below. Just as you can check the solution to an equation, you can check a solution to an inequality. First, you check the end point by substituting it in the related equation.
It can be solved many way, here we will solve it by completing the square: Move the −7 to the right side of the inequality: W2 − 8W ≤ −7. Complete the square on the left side of the inequality and balance this by adding the same value to the right side of the inequality: W2 − 8W + 16 ≤ −7 + 16. Simplify: (W − 4)2 ≤ 9.
Multi-step linear inequalities. Solve for z . Reduce any fractions to lowest terms. Don't round your answer, and don't use mixed fractions. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world ...
They describe relationships between variables and constants and are essential in solving problems involving ranges of values, constraints and conditions. ... Rational Inequality: Solve the inequality: (x-2) / (x+1) > 0. ... Equations and inequalities are both mathematical sentences formed by relating two expressions to each other. In an ...
There are different types of math problems.An example of radical equations and inequalities practice question is [tex]\sqrt{x}[/tex] = 5. What is a radical inequality? The term radical inequality is known to be a form of an inequality that maintains a variable expression that is present within it.. For the above question, find the [tex]\sqrt{x}[/tex] = 5
Of course! The math on the SAT covers several areas, and is divided into two sections. Here's a basic breakdown: 1. **Heart of Algebra:** This includes linear equations and systems. This section is all about analyzing and solving problems involving linear relationships. This means you'll be dealing with mathematical expressions, linear equations, linear inequalities, and linear functions.
1) If you multiply / divide both sides of the equation by a negative value, you need to reverse the inequality. 2) Equations create 1 solution. With inequalities, you will have a large number of solutions. For example: x>1 has a solution set of all real numbers larger than 1. Hope this helps.
In this paper, we develop and study the mixed finite element method for a hemivariational inequality of the stationary Navier-Stokes equations (NS hemivariational inequality). The NS hemivariational inequality models the motion of a viscous ...
One-step inequalities. Solve for x . Your answer must be simplified. Learn for free about math, art, computer programming, economics, physics, chemistry, biology, medicine, finance, history, and more. Khan Academy is a nonprofit with the mission of providing a free, world-class education for anyone, anywhere.
Anthropic CEO says we need to think bigger than a universal basic income if we want to solve the AI inequality problem. Lakshmi Varanasi. 2024-06-23T21:17:26Z An curved arrow pointing right. Share ...
This unit is about writing and solving one-variable equations and inequalities, and applying these concepts to real-world problems. We'll also explore financial concepts including simple and compound interest, and factors that go into taking out a loan. **Unit guides are here!** Power up your classroom with engaging strategies, tools, and activities from Khan Academy's learning experts ...