What Is Constrained Optimization?
Last updated: March 18, 2024
- Math and Logic
- Optimization

1. Introduction
Constrained optimization, also known as constraint optimization, is the process of optimizing an objective function with respect to a set of decision variables while imposing constraints on those variables .
In this tutorial, we’ll provide a brief introduction to constrained optimization, explore some examples, and introduce some methods to solve constrained optimization problems.
2. Constrained Optimization
In a constrained optimization problem, the objective function is either a cost function (to be minimized) or a reward/utility function (to be maximized).
Now, let’s examine situations where a function is constrained. A constraint is a hard limit we place on a variable’s value to prevent the objective function from going forever in certain directions:
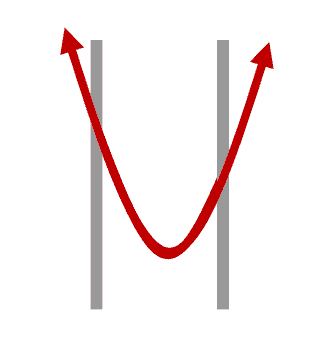
2.1. Optimum’s Location
With nonlinear functions, the optima (maximum or minimum values) can either occur at the boundaries or between them:
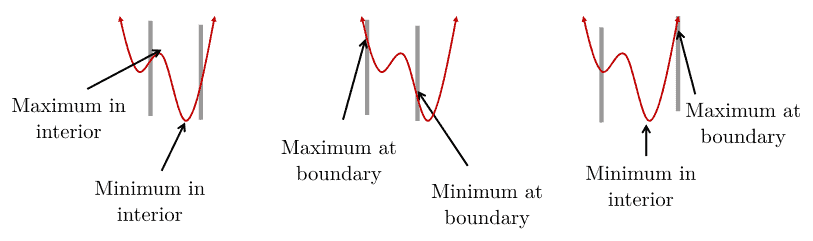
As we can see, the maximum or minimum values can occur in the interior or at boundaries.
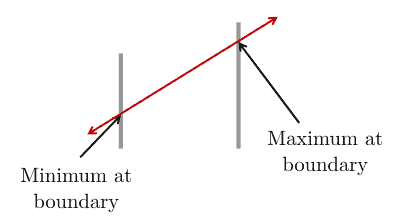
In contrast, with linear functions, the maximum or minimum values occur only at boundaries:
3. Forms of Constrained Optimization Problems
The following formulation describes the general (canonical) form of a constrained minimization problem:
If we need to maximize the objective function, e.g., the utilization efficiency of network resources, we can negate it to make it fit the general form:
3.1. Types of Constrained Optimization Problems
Depending on the objective function and constraints, there are several types of constrained optimization problems.
Linear Programming (LP) covers the cases in which the objective function is linear and all constraints are also linear. If all decision variables are integers, then we’ll have an Integer Linear Programming (ILP) problem. If only some of the decision variables are integers (the remaining are continuous), that’s a Mixed Integer Linear Programming (MILP) problem.
For example:
Nonlinear Programming (NLP) refers to the problems where the objective function or some constraints are nonlinear. Similar to linear programming, there are Integer Nonlinear Programming (INLP) and Mixed Integer Nonlinear Programming (MINLP).
Here’s an example of a problem with nonlinear constraints:
Finally, Quadratic Programming (QP) problems are those with linear constraints but the objective function is quadratic. Similar to linear programming and nonlinear programming problems, we also have Integer Quadratic Programming (IQP) and Mixed Integer Quadratic Programming (MIQP) problems.
For instance:
4. Real-World Example
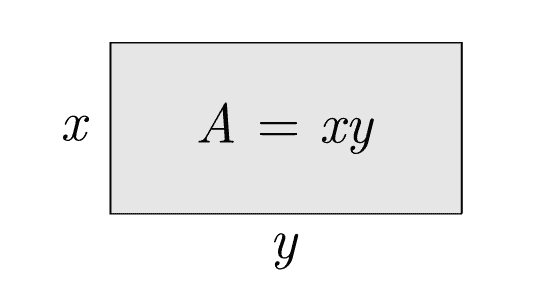
5. Solving Constrained Problems
Let’s now see how we can solve constrained optimization problems.
5.1. Mathematical Methods
There is, unfortunately, no universal method for solving all types of optimization problems.
Different proposed methods are tailored to particular types of optimization problems. The following table lists some classical mathematical methods for solving constrained optimization problems:
| Method | Pros | Cons | |
|---|---|---|---|
| Equality constraints | Substitution method | Easy to understand, simple to calculate | May fail when dealing with nonlinear constraints, or discontinuous objective function |
| Lagrange multiplier | Can solve NLP with complex and inequality constraints. | Must be altered to compensate for inequality constraints. Only practical for small problems | |
| Branch-and-bound algorithms | Lower complexity compared to other algorithms | Time-consuming, difficult to apply parallelization | |
| Simplex method | Memory efficient, numerically stable, high iteration speed | Not so good for large problems, difficult to apply parallelization | |
| Interior-point method | Require few iterations, easy to parallelize | Not suitable when needing a quick and degenerate basic solution | |
| Inequality constraints | Ellipsoid method (for QP) | Polynomial-time solvability for LPs | Numerical instability and poor performance in practice |
| Karush–Kuhn–Tucker (KKT) approach (for NLP) | Useful (and necessary) for checking the optimality of a solution | Not sufficient if the objective function is non-convex |
Most of these methods, such as the branch-and-bound algorithm , are exact. Exact optimization techniques are guaranteed to find the optimal solution. The price for such guarantees is that they can take a lot of time to complete. In contrast, inexact methods don’t guarantee finding the optimum but usually produce a sufficiently good solution quickly. Metaheuristics such as the Grey-Wolf Optimization algorithm fall into the category of inexact methods and are frequently used when we need to find any solution quickly.
5.2. The Substitution Method
Let’s explain the substitution method using a simple example with an equality constraint:
Since we have a simple equality constraint, we can use the substitution method . We use this method mostly for problems with an equality constraint from which it’s easy to express one variable in terms of others. If we’re lucky, we can substitute the variable in the objective function and get a form that isn’t hard to solve by hand.
In our example, the constraint gives us a simple substitution:
As a result, we can rewrite the objective function:
5.3. Optimization Solvers
The following table summarizes some well-known software tools for constrained optimization problems :
| Solvers | Description | Supported interface |
|---|---|---|
| CPLEX | For general purposes. The toolbox includes solvers for LP, ILP, MILP, convex and non-convex QP problems, etc. | C++, C#, Java, MATLAB, Python |
| GPLK | For LP, MIP and other related problems | C, Java |
| Gurobi | For general purposes, including solvers for LP, ILP, MILP, MIQP, etc. | C, C++, .NET, Java, MATLAB, Python, R, AMPL, C, C++, Java, MATLAB, Python, R |
| lp_solve | For MILP problems | MATLAB, Octave, Python, R, etc. |
| MATLAB, Optim. Toolbox | For general purposes, including solvers for LP, ILP, MILP, etc. | MATLAB |
| SCIP | For MIP problems | AMPL, C, C++, Java, MATLAB, Python |
They all perform built-in exact methods (e.g., simplex ) and usually combine them with inexact algorithms to reach a solution faster . For instance, CPLEX uses a node heuristic along with the branch-and-cut algorithm .
6. Conclusion
In this article, we covered the principles of constrained optimization. There are several types of constrained optimization problems and many methods for solving them. Which one is the best depends on the particular problem at hand.
Introduction to Constrained Optimization in the Wolfram Language
Optimization Problems
The following describes constrained optimization problems more precisely, restricting the discussion to minimization problems for brevity.
Global Optimization
Local Optimization
A local minimum may not be a global minimum. A global minimum is always a local minimum.
Solving Optimization Problems
Wolfram Language functions for constrained optimization include Minimize , Maximize , NMinimize , and NMaximize for global constrained optimization, FindMinimum for local constrained optimization, and LinearOptimization for efficient and direct access to linear optimization methods. The following table briefly summarizes each of the functions.
| , | numeric local optimization | linear programming methods, nonlinear interior point algorithms, utilize second derivatives | , | numeric global optimization | linear programming methods, Nelder-Mead, differential evolution, simulated annealing, random search | , | exact global optimization | linear programming methods, cylindrical algebraic decomposition, Lagrange multipliers and other analytic methods, integer linear programming | linear optimization | linear optimization methods (simplex, revised simplex, interior point) |
Summary of constrained optimization functions.
Here is a decision tree to help in deciding which optimization function to use.
Related Tech Notes
- Constrained Optimization
- Linear Optimization
- Numerical Nonlinear Local Optimization
- Numerical Nonlinear Global Optimization
- Exact Global Optimization
Enable JavaScript to interact with content and submit forms on Wolfram websites. Learn how
Mathematical tools for intermediate economics classes Iftekher Hossain
Calculus of Multivariable Functions
Use of Partial Derivatives in Economics; Constrained Optimization
Although there are examples of unconstrained optimizations in economics, for example finding the optimal profit, maximum revenue, minimum cost, etc., constrained optimization is one of the fundamental tools in economics and in real life. Consumers maximize their utility subject to many constraints, and one significant constraint is their budget constraint. Even Bill Gates cannot consume everything in the world and everything he wants. Can Mark Zuckerberg buy everything? Similarly, while maximizing profit or minimizing costs, the producers face several economic constraints in real life, for examples, resource constraints, production constraints, etc.
The commonly used mathematical technique of constrained optimizations involves the use of Lagrange multiplier and Lagrange function to solve these problems followed by checking the second order conditions using the Bordered Hessian. When the objective function is a function of two variables, and there is only one equality constraint , the constrained optimization problem can also be solved using the geometric approach discussed earlier given that the optimum point is an interior optimum. It should be mentioned again that we will not address the second-order sufficient conditions in this chapter.
Example 1: Maximize utility \(u = f(x,y) = xy\) subject to the constraint \(g(x,y) = x + 4y = 240\). Here the price of per unit \(x\) is \(1\), the price of \(y\) is \(4\) and the budget available to buy \(x\) and \(y\) is \(240\). Solve the problem using the geometric approach .
Here the optimization problem is: Objective function: maximize \(u(x,y) = xy\) Subject to the constraint: \(g(x,y) = x + 4y = 240\). Step 1: \(-\frac{f_{x}}{f_{y}} = -\frac{y}{x}\) (Slope of the indifference curve) Step 2: \(-\frac{g_{x}}{g_{y}} = -\frac{1}{4}\) (Slope of the budget line) Step 3: \(-\frac{f_{x}}{f_{y}} = -\frac{g_{x}}{g_{y}}\) (Utility maximization requires the slope of the indifference curve to be equal to the slope of the budget line.) $$-\frac{y}{x} = -\frac{1}{4}$$ $$x = 4y$$ Step 4: From step 3, use the relation between \(x\) and \(y\) in the constraint function to get the critical values. $$x + 4y = 240$$ $$4y + 4y = 240$$ $$8y = 240$$ $$y = 30$$ Using \(y = 30\) in the relation \(x = 4y\), we get \(x = 4 \times 30 = 120\) Utility may be maximized at \((120, 30)\).
Suppose a consumer consumes two goods, \(x\) and \(y\) and has utility function \(u(x,y) = xy\). He has a budget of \($400\). The price of \(x\) is \(P_{x} = 10\) and the price of \(y\) is \(P_{y} = 20\). Find his optimal consumption bundle using the Lagrange method .
Here the optimization problem is: Objective function: maximize \(u(x,y) = xy\) Subject to the constraint: \(g(x,y) = 10x + 20y = 400\). This is a problem of constrained optimization. Form the Lagrange function: $$L(x,y,\mu ) \equiv \color{red}{f(x,y)} - \mu (\color{purple}{g(x,y) - k})$$ $$L(x,y,\mu ) \equiv xy - \mu (10x + 20y - 400)$$ Set each first order partial derivative equal to zero: $$\frac{\partial L}{\partial x} = y - 10\mu = 0 \qquad\qquad\qquad \text{(1)}$$ $$\frac{\partial L}{\partial y} = x - 20\mu = 0 \qquad\qquad\qquad \text{(2)}$$ $$\frac{\partial L}{\partial \mu} = -(10x + 20y - 400) = 0 \quad \text{(1)}$$ From equations (1) and (2) we find: $$x = 2y$$ Use \(x = 2y\) in equation (3) to get: $$10x + 20y = 400$$ $$40y = 400$$ $$\bf{y = 10}$$ $$\bf{x = 2y = 20}$$ See the graph below.
Example 3: The effects of a change in price
Suppose a consumer consumes two goods, \(x\) and \(y\) and has the utility function \(U(x,y) = xy\). He has a budget of \($400\). The price of \(x\) is \(P_{x} = 10\) and the price of \(y\) is \(P_{y} = 20\).
- Find his optimal consumption bundle.
- What happens when the price of \(x\) falls to \(P_{x} = 5\), other factors remaining constant?
- When \(P_{x} = 10\), the optimal bundle \((x,y)\) is \((20,10)\) (See Example 2)
- When the price of \(x\) falls to \(P_{x} = 5\), New budget equation is: \(5x + 20y = 400\) Slope of the indifference curve \(= -\frac{y}{x}\) Slope of the budget line \(= -\frac{5}{20} = -\frac{1}{4}\) Optimality requires that the slope of the indifference curve equals to the slope of the budget line: $$-\frac{y}{x} = -\frac{1}{4}$$ $$x = 4y$$ Use the relation \(x = 4y\) in the new budget equation: $$5x + 20y = 400$$ $$5(4y) + 20y = 400 \;\;\;$$ $$20y + 20y = 400$$ $$\qquad\quad\;\; y = 10$$ $$x = 4y = 4(10) = 40$$ When the price of \(x\) falls while all other factors remain constant, in this typical example, the consumption of \(x\) increases.
Example 4: The effects of a change in income
Suppose a consumer consumes two goods, \(x\) and \(y\) and has utility function \(U(x,y) = xy\). He has a budget of \($400\). The price of \(x\) is \(P_{x} = $10\) and the price of \(y\) is \(P_{y} = $20\).
- What happens when the when the income rises to \(B = 800\), other factors remaining constant?
- When \(P_{x} = $10\), \(P_{y} = $20\) and \(B = 400\), the optimal bundle is \((20,10)\). (See example 2)
- When the income increases to \(800\) while other factors remain constant, New budget equation is: \(10x + 20y = 800\) Slope of the indifference curve \(= -\frac{y}{x}\) Slope of the budget line \(= -\frac{10}{20} = -\frac{1}{2}\) Optimality requires that the slope of the indifference curve equals the slope of the budget line: $$-\frac{y}{x} = -\frac{1}{2} \;\;$$ $$x = 2y$$ Use the relation, \(x = 2y\) in the new budget equation: $$10x + 20y = 800$$ $$10(2y) + 20y = 800 \quad$$ $$\; 20y + 20y = 800$$ $$\qquad\quad\;\; y = 20$$ $$\qquad\qquad\qquad\qquad\qquad\;\; x = 2y = 2(20) = 40 \quad$$ When consumer’s income increases, while other factors remain constant, for typical goods discussed in this example, consumption of both goods increases.


Wolfram|Alpha Widgets Overview Tour Gallery Sign In
Share this page.
- StumbleUpon
- Google Buzz
Output Type
Output width, output height.
To embed this widget in a post, install the Wolfram|Alpha Widget Shortcode Plugin and copy and paste the shortcode above into the HTML source.
To embed a widget in your blog's sidebar, install the Wolfram|Alpha Widget Sidebar Plugin , and copy and paste the Widget ID below into the "id" field:
Save to My Widgets
Build a new widget.
We appreciate your interest in Wolfram|Alpha and will be in touch soon.
Help Center Help Center
- Help Center
- Trial Software
- Product Updates
- Documentation
Solve a Constrained Nonlinear Problem, Problem-Based
Typical optimization problem.
This example shows how to solve a constrained nonlinear optimization problem using the problem-based approach. The example demonstrates the typical work flow: create an objective function, create constraints, solve the problem, and examine the results.
If your objective function or nonlinear constraints are not composed of elementary functions, you must convert the nonlinear functions to optimization expressions using fcn2optimexpr . See the last part of this example, Alternative Formulation Using fcn2optimexpr , or Convert Nonlinear Function to Optimization Expression .
For the solver-based approach to this problem, see Constrained Nonlinear Problem Using Optimize Live Editor Task or Solver .
Problem Formulation: Rosenbrock's Function
Consider the problem of minimizing the logarithm of 1 plus Rosenbrock's function
f ( x ) = log ( 1 + 1 0 0 ( x 2 - x 1 2 ) 2 + ( 1 - x 1 ) 2 ) ,
over the unit disk , meaning the disk of radius 1 centered at the origin. In other words, find x that minimizes the function f ( x ) over the set x 1 2 + x 2 2 ≤ 1 . This problem is a minimization of a nonlinear function subject to a nonlinear constraint.
Rosenbrock's function is a standard test function in optimization. It has a unique minimum value of 0 attained at the point [1,1] , and therefore f ( x ) attains the same minimum at the same point. Finding the minimum is a challenge for some algorithms because the function has a shallow minimum inside a deeply curved valley. The solution for this problem is not at the point [1,1] because that point does not satisfy the constraint.
This figure shows two views of the function f ( x ) function in the unit disk. Contour lines lie beneath the surface plot.
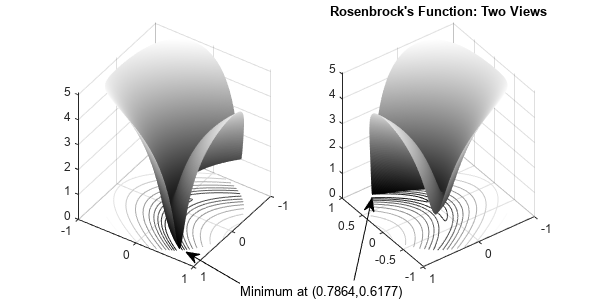
The rosenbrock function handle calculates the function f ( x ) at any number of 2-D points at once. This Vectorization speeds the plotting of the function, and can be useful in other contexts for speeding evaluation of a function at multiple points.
The function f ( x ) is called the objective function. The objective function is the function you want to minimize. The inequality x 1 2 + x 2 2 ≤ 1 is called a constraint. Constraints limit the set of x over which a solver searches for a minimum. You can have any number of constraints, which are inequalities or equations.
Define Problem Using Optimization Variables
The problem-based approach to optimization uses optimization variables to define objective and constraints. There are two approaches for creating expressions using these variables:
For elementary functions such as polynomials or trigonometric functions, write expressions directly in the variables.
For other types of functions, convert functions to optimization expressions using fcn2optimexpr . See Alternative Formulation Using fcn2optimexpr at the end of this example.
For this problem, both the objective function and the nonlinear constraint are elementary, so you can write the expressions directly in terms of optimization variables. Create a 2-D optimization variable named 'x' .
Create the objective function as an expression of the optimization variable.
Create an optimization problem named prob having obj as the objective function.
Create the nonlinear constraint as a polynomial of the optimization variable.
Include the nonlinear constraint in the problem.
Review the problem.
Solve Problem
To solve the optimization problem, call solve . The problem needs an initial point, which is a structure giving the initial value of the optimization variable. Create the initial point structure x0 having an x -value of [0 0] .
Examine Solution
The solution shows exitflag = OptimalSolution . This exit flag indicates that the solution is a local optimum. For information on trying to find a better solution, see When the Solver Succeeds .
The exit message indicates that the solution satisfies the constraints. You can check that the solution is indeed feasible in several ways.
Check the reported infeasibility in the constrviolation field of the output structure.
An infeasibility of 0 indicates that the solution is feasible.
Compute the infeasibility at the solution.
Again, an infeasibility of 0 indicates that the solution is feasible.
Compute the norm of x to ensure that it is less than or equal to 1.
The output structure gives more information on the solution process, such as the number of iterations (23), the solver ( fmincon ), and the number of function evaluations (44). For more information on these statistics, see Tolerances and Stopping Criteria .
Alternative Formulation Using fcn2optimexpr
For more complex expressions, write function files for the objective or constraint functions, and convert them to optimization expressions using fcn2optimexpr . For example, the basis of the nonlinear constraint function is in the disk.m file:
Convert this function file to an optimization expression.
Furthermore, you can also convert the rosenbrock function handle, which was defined at the beginning of the plotting routine, into an optimization expression.
Create an optimization problem using these converted optimization expressions.
View the new problem.
Solve the new problem. The solution is essentially the same as before.
For the list of supported functions, see Supported Operations for Optimization Variables and Expressions .
Related Topics
- Constrained Nonlinear Problem Using Optimize Live Editor Task or Solver
- First Choose Problem-Based or Solver-Based Approach
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
- Switzerland (English)
- Switzerland (Deutsch)
- Switzerland (Français)
- 中国 (English)
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
- América Latina (Español)
- Canada (English)
- United States (English)
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- United Kingdom (English)
Asia Pacific
- Australia (English)
- India (English)
- New Zealand (English)
Contact your local office
- DOI: 10.3233/idt-240306
- Corpus ID: 270840726

A new accurate and fast convergence cuckoo search algorithm for solving constrained engineering optimization problems
- Mahdi Abdollahi , Asgarali Bouyer , Bahman Arasteh
- Published in International Journal of… 20 June 2024
- Engineering
39 References
Optimization of constraint engineering problems using robust universal learning chimp optimization, a new chaotic lévy flight distribution optimization algorithm for solving constrained engineering problems, single and multiple odor source localization using hybrid nature-inspired algorithm, improved cuckoo optimization algorithm for solving systems of nonlinear equations, a hybrid differential evolution augmented lagrangian method for constrained numerical and engineering optimization, imperialist competitive algorithm for solving systems of nonlinear equations, investigating multi-view differential evolution for solving constrained engineering design problems, water cycle algorithm - a novel metaheuristic optimization method for solving constrained engineering optimization problems, evaluating differential evolution with penalty function to solve constrained engineering problems, an effective hybrid genetic algorithm with flexible allowance technique for constrained engineering design optimization, related papers.
Showing 1 through 3 of 0 Related Papers

- Advanced Search
A novel stepsize for gradient descent method
New citation alert added.
This alert has been successfully added and will be sent to:
You will be notified whenever a record that you have chosen has been cited.
To manage your alert preferences, click on the button below.
New Citation Alert!
Please log in to your account
Information & Contributors
Bibliometrics & citations, view options, recommendations, interior gradient and epsilon-subgradient descent methods for constrained convex minimization.
We extend epsilon-subgradient descent methods for unconstrained nonsmooth convex minimization to constrained problems over polyhedral sets, in particular over R p +. This is done by replacing the usual squared quadratic regularization term used in ...
Inexact projected gradient method for vector optimization
In this work, we propose an inexact projected gradient-like method for solving smooth constrained vector optimization problems. In the unconstrained case, we retrieve the steepest descent method introduced by Graña Drummond and Svaiter. In the ...
Proximal level bundle methods for convex nondifferentiable optimization, saddle-point problems and variational inequalities
We study proximal level methods for convex optimization that use projections onto successive approximations of level sets of the objective corresponding to estimates of the optimal value. We show that they enjoy almost optimal efficiency estimates. We ...
Information
Published in.
Elsevier Science Publishers B. V.
Netherlands
Publication History
Author tags.
- Convex programming
- Gradient descent method
- Nonlinear programming
- Projected gradient method
- Constrained optimization problem
- Rapid-communication
Contributors
Other metrics, bibliometrics, article metrics.
- 0 Total Citations
- 0 Total Downloads
- Downloads (Last 12 months) 0
- Downloads (Last 6 weeks) 0
View options
Login options.
Check if you have access through your login credentials or your institution to get full access on this article.
Full Access
Share this publication link.
Copying failed.
Share on social media
Affiliations, export citations.
- Please download or close your previous search result export first before starting a new bulk export. Preview is not available. By clicking download, a status dialog will open to start the export process. The process may take a few minutes but once it finishes a file will be downloadable from your browser. You may continue to browse the DL while the export process is in progress. Download
- Download citation
- Copy citation
We are preparing your search results for download ...
We will inform you here when the file is ready.
Your file of search results citations is now ready.
Your search export query has expired. Please try again.
Help | Advanced Search
Mathematics > Optimization and Control
Title: a fast single-loop primal-dual algorithm for non-convex functional constrained optimization.
Abstract: Non-convex functional constrained optimization problems have gained substantial attention in machine learning and signal processing. This paper develops a new primal-dual algorithm for solving this class of problems. The algorithm is based on a novel form of the Lagrangian function, termed {\em Proximal-Perturbed Augmented Lagrangian}, which enables us to develop an efficient and simple first-order algorithm that converges to a stationary solution under mild conditions. Our method has several key features of differentiation over existing augmented Lagrangian-based methods: (i) it is a single-loop algorithm that does not require the continuous adjustment of the penalty parameter to infinity; (ii) it can achieves an improved iteration complexity of $\widetilde{\mathcal{O}}(1/\epsilon^2)$ or at least ${\mathcal{O}}(1/\epsilon^{2/q})$ with $q \in (2/3,1)$ for computing an $\epsilon$-approximate stationary solution, compared to the best-known complexity of $\mathcal{O}(1/\epsilon^3)$; and (iii) it effectively handles functional constraints for feasibility guarantees with fixed parameters, without imposing boundedness assumptions on the dual iterates and the penalty parameters. We validate the effectiveness of our method through numerical experiments on popular non-convex problems.
| Subjects: | Optimization and Control (math.OC) |
| Cite as: | [math.OC] |
| (or [math.OC] for this version) | |
| Focus to learn more arXiv-issued DOI via DataCite |
Submission history
Access paper:.
- HTML (experimental)
- Other Formats
References & Citations
- Google Scholar
- Semantic Scholar
BibTeX formatted citation
Bibliographic and Citation Tools
Code, data and media associated with this article, recommenders and search tools.
- Institution
arXivLabs: experimental projects with community collaborators
arXivLabs is a framework that allows collaborators to develop and share new arXiv features directly on our website.
Both individuals and organizations that work with arXivLabs have embraced and accepted our values of openness, community, excellence, and user data privacy. arXiv is committed to these values and only works with partners that adhere to them.
Have an idea for a project that will add value for arXiv's community? Learn more about arXivLabs .
Approximation Methods for a Class of Non-Lipschitz Mathematical Programs with Equilibrium Constraints
- Published: 01 July 2024
Cite this article

- Lei Guo ORCID: orcid.org/0009-0007-2881-390X 1 &
- Gaoxi Li 2
We consider how to solve a class of non-Lipschitz mathematical programs with equilibrium constraints (MPEC) where the objective function involves a non-Lipschitz sparsity-inducing function and other functions are smooth. Solving the non-Lipschitz MPEC is highly challenging since the standard constraint qualifications fail due to the existence of equilibrium constraints and the subdifferential of the objective function is unbounded due to the existence of the non-Lipschitz function. On the one hand, for tackling the non-Lipschitzness of the objective function, we introduce a novel class of locally Lipschitz approximation functions that consolidate and unify a diverse range of existing smoothing techniques for the non-Lipschitz function. On the other hand, we use the Kanzow and Schwartz regularization scheme to approximate the equilibrium constraints since this regularization can preserve certain perpendicular structure as in equilibrium constraints, which can induce better convergence results. Then an approximation method is proposed for solving the non-Lipschitz MPEC and its convergence is established under weak conditions. In contrast with existing results, the proposed method can converge to a better stationary point under weaker qualification conditions. Finally, a computational study on the sparse solutions of linear complementarity problems is presented. The numerical results demonstrate the effectiveness of the proposed method.
This is a preview of subscription content, log in via an institution to check access.
Access this article
Subscribe and save.
- Get 10 units per month
- Download Article/Chapter or Ebook
- 1 Unit = 1 Article or 1 Chapter
- Cancel anytime
Price includes VAT (Russian Federation)
Instant access to the full article PDF.
Rent this article via DeepDyve
Institutional subscriptions

Similar content being viewed by others

Necessary optimality conditions and exact penalization for non-Lipschitz nonlinear programs
Solving mathematical programs with equilibrium constraints, smoothing partial exact penalty splitting method for mathematical programs with equilibrium constraints.
Andreani, R., Haeser, G., María, L.S., Silva, P.J.: A relaxed constant positive linear dependence constraint qualification and applications. Math. Prog. 135 (1–2), 255–273 (2012)
Article MathSciNet Google Scholar
Andreani, R., Haeser, G., Secchin, L.D., Silva, P.J.: New sequential optimality conditions for mathematical programs with complementarity constraints and algorithmic consequences. SIAM J. Optim. 29 (4), 3201–3230 (2019)
Bian, W., Chen, X.: Worst-case complexity of smoothing quadratic regularization methods for non-Lipschitzian optimization. SIAM J. Optim. 23 (3), 1718–1741 (2013)
Bouza, G., Still, G.: Mathematical programs with complementarity constraints: Convergence properties of a smoothing method. Math. Oper. Res. 32 (2), 467–483 (2007)
Chen, X., Fukushima, M.: A smoothing method for a mathematical program with \(p\) -matrix linear complementarity constraints. Comput. Opt. Appl. 27 (3), 223–246 (2004)
Chen, X., Xiang, S.: Sparse solutions of linear complementarity problems. Math. Prog. 159 (1–2), 539–556 (2016)
Chen, X., Zhou, W.: Convergence of the reweighted \(l_1\) minimization algorithm for \(l_2-l_p\) minimization. Comput. Opt. Appl. 59 (3), 47–61 (2014)
Article Google Scholar
Fletcher, R., Leyffer, S., Ralph, D., Scholtes, S.: Local convergence of SQP methods for mathematical programs with equilibrium constraints. SIAM J. Opt. 17 (1), 259–286 (2006)
Guo, L., Chen, X.: Mathematical programs with complementarity constraints and a non-Lipschitz objective: optimality and approximation. Math. Prog. 185 , 455–485 (2021)
Guo, L., Deng, Z.: A new augmented Lagrangian method for MPCCs-Theoretical and numerical comparison with existing augmented Lagrangian methods. Math. Oper. Res. 47 (2), 1229–1246 (2022)
Guo, L., Lin, G., Ye, J.J.: Stability analysis for parametric mathematical programs with geometric constraints and its applications. SIAM J. Opt. 22 (3), 1151–1176 (2012)
Guo, L., Lin, G.H.: Notes on some constraint qualifications for mathematical programs with equilibrium constraints. J. Opt. Theory Appl. 156 (3), 600–616 (2013)
Hintermöller, M., Wu, T.: Nonconvex TV \(^q\) -models in image restoration: analysis and a trust-region regularization-based superlinearly convergent solver. SIAM J. Imag. Sci. 6 (3), 1385–1415 (2013)
Hoheisel, T., Kanzow, C., Schwartz, A.: Theoretical and numerical comparison of relaxation methods for mathematical programs with complementarity constraints. Math. Prog. 137 (1–2), 257–288 (2013)
Izmailov, A.F., Solodov, M.V., Uskov, E.I.: Global convergence of augmented Lagrangian methods applied to optimization problems with degenerate constraints, including problems with complementarity constraints. SIAM J. Opt. 22 (4), 1579–1606 (2012)
Kadrani, A., Dussault, J.P., Benchakroun, A.: A new regularization scheme for mathematical programs with complementarity constraints. SIAM J. Opt. 20 (1), 78–103 (2009)
Kanzow, C., Schwartz, A.: Mathematical programs with equilibrium constraints: Enhanced Fritz John-conditions, new constraint qualifications, and improved exact penalty results. SIAM J. Opt. 20 (5), 2730–2753 (2010)
Kanzow, C., Schwartz, A.: A new regularization method for mathematical programs with complementarity constraints with strong convergence properties. SIAM J. Opt. 23 (2), 770–798 (2013)
Kanzow, C., Schwartz, A.: The price of inexactness: Convergence properties of relaxation methods for mathematical programs with complementarity constraints revisited. Math. Oper. Res. 40 (2), 253–275 (2015)
Lai, M.J., Wang, J.: An unconstrained \(l_q\) minimization with \(0<l_q<1\) for sparse solution of underdetermined linear systems. SIAM J. Opt. 21 (1), 82–101 (2011)
Lin, G.H., Fukushima, M.: New relaxation method for mathematical programs with complementarity constraints. J. Opt. Theory Appl. 118 , 81–116 (2003)
Liu, G., Ye, J.: Merit-function piecewise SQP algorithm for mathematical programs with equilibrium constraints. J. Opt. Theory Appl. 135 (3), 623–641 (2007)
Lu, Z.: Iterative reweighted minimization methods for \(l_p\) regularized unconstrained nonlinear programming. Math. Prog. 147 (1–2), 277–307 (2014)
Luo, H., Sun, X., Xu, Y.: Convergence properties of modified and partially-augmented Lagrangian methods for mathematical programs with complementarity constraints. J. Opt. Theory Appl. 145 (3), 489–506 (2010)
Outrata, J.V.: Optimality conditions for a class of mathematical programs with equilibrium constraints. Math. Oper. Res. 24 (3), 627–644 (1999)
Ramos, A.: Mathematical programs with equilibrium constraints: a sequential optimality condition, new constraint qualifications and algorithmic consequences. Opt. Methods Softw. 36 (1), 45–81 (2021)
Rockafellar, R.T., Wets, R.J.B.: Variational Analysis. Springer, Berlin (2010)
Google Scholar
Scheel, H., Scholtes, S.: Mathematical programs with complementarity constraints: Stationarity, optimality, and sensitivity. Math. Oper. Res. 25 (1), 1–22 (2000)
Scholtes, S.: Convergence properties of a regularization scheme for mathematical programs with complementarity constraints. SIAM J. Opt. 11 (4), 918–936 (2001)
Ye, J.J.: Constraint qualifications and KKT conditions for bilevel programming problems. Math. Oper. Res. 31 (4), 811–824 (2006)
Ye, J.J., Zhu, D., Zhu, Q.: Exact penalization and necessary optimality conditions for generalized bilevel programming problems. SIAM J. Opt. 7 (2), 481–507 (1997)
Download references
Acknowledgements
The authors are grateful to the two referees for their helpful comments and constructive suggestions. In particular, we thank one of the referees for suggesting the use of weaker qualifications than MPEC-RCPLDQC when studying the convergence. The first author was supported by the National Natural Science Foundation of China (Grants 72131007, 72140006, 12271161) and the Natural Science Foundation of Shanghai (Grant 22ZR1415900). This second author was supported by the Project of National Center for Applied Mathematics (Grant ncamc2021-msxm01) and the National Natural Science Foundation of China (Grant 11901068).
Author information
Authors and affiliations.
School of Business, East China University of Science and Technology, Shanghai, 200237, China
School of Mathematics and Statistics, Chongqing Technology and Business University, Chongqing, 400067, China
You can also search for this author in PubMed Google Scholar
Corresponding author
Correspondence to Lei Guo .
Additional information
Communicated by Sofia Giuffre.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix: The Convergence When Using the Regularization by Kadrani et al.
When using the regularization scheme by Kadrani et al., our approximation problem becomes
where \(\Phi _i^{KDB}(x;t):=(H_i(x)-t)(G_i(x)-t)\) for all \(i\in \{1,\ldots ,m\}\) . By a straightforward calculation, we have
Assume that \(t^{k}\downarrow 0\) and \(\sigma ^{k}\downarrow 0\) as \(k\rightarrow \infty \) . Let \(x^k\) be a stationary solution of \(\mathrm{(P_{\sigma ^k,t^k}^{KDB})}\) , and \(x^*\) be an accumulation point of \(\{x^k\}\) . If MPEC-CCQC holds at \(x^*\) , then \(x^*\) is an M-stationary point of problem ( 1 ).
Recall that \(x^k\) is a stationary point of problem \(\mathrm{(P_{\sigma ^k,t^k}^{KDB})}\) if there exist multipliers \((\alpha ^k,\beta ^k,\pi ^k,\rho ^k,\gamma ^k)\) such that
Then ( 36 ) can be rewritten as
where \(\xi ^k_i \in \partial \varphi (D_i^\top x^k; \sigma ^k_i)\) for all \(i=1,\ldots ,r\) . By the definition of \(\varphi \) , it is easy to see that
We next show that there exists a sequence \(z^k\rightarrow F(x^*)\) such that ( 41 ) holds with \(\alpha _i^k\in {{\mathcal {N}}}_{(0,\infty ]}(z_i^k)\) and \((\mu _i^k,\nu _i^k)\in {{\mathcal {N}}}_{{\mathcal {C}}}(z_i^k)\) . Let \(z^k = (D_i^Tx^*\ i\in {{\mathcal {I}}}_0^*,g(x^k),h(x^k),R(x^*))\) . It is clear that \(z^k\in \Lambda \) . By ( 37 ), it is easy to see that \(\alpha _i^k\in {{\mathcal {N}}}_{(0,\infty ]}(z_i^k)\) for all \(i=1,\ldots ,q\) . One can easily observe that if \(i\in {{\mathcal {I}}}_{+0}^*\) , then \(G_i(x^*)>0\) . Thus \(\pi _i^k=0\) by ( 38 ) and \(\gamma _i^k(H_i(x^k)-t_k)=0\) by ( 40 ). Hence \(\mu _i^k=\pi _i^k-\gamma _i^k(H_i(x^k)-t_k)=0\) for \(i\in {{\mathcal {I}}}_{+0}^*\) . In the same way, we have \(\nu _i^k=0\) for \(i\in {{\mathcal {I}}}_{0+}^*\) . Moreover, it is easy to see that if \(\mu _i^k<0\) , then \(\pi _i^k=0\) and \(\gamma _i^k(H_i(x^k)-t_k)>0\) . Thus, by ( 40 ), it follows \(G_i(x^k)-t_k = 0\) and by ( 39 ), it follows \(\rho _i^k=0\) . Hence \(\nu _i^k=\rho _i^k-\gamma _i^k(G_i(x^k)-t_k)=0\) and then \(\mu _i^k\nu _i^k=0\) if \(\mu _i^k<0\) . In the same way, we can have \(\mu _i^k\nu _i^k=0\) if \(\nu _i^k<0\) . Consequently, we have \(\mu _i^k>0,\nu _i^k>0\) or \(\mu _i^k\nu _i^k=0\) for all i . Thus, by the expression of the normal cone to \({{\mathcal {C}}}\) , we have \((\mu _i^k,\nu _i^k)\in {{\mathcal {N}}}_{{\mathcal {C}}}(z_i^k)\) .
Based on the above discussions and the expression of the normal cone to \(\Lambda \) , ( 41 ) can be written as
Since MPEC-CCQC holds at \(x^*\) , it follows that
indicating that \(x^*\) is an M-stationary point by Proposition 2 . \(\square \)
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
Reprints and permissions
About this article
Guo, L., Li, G. Approximation Methods for a Class of Non-Lipschitz Mathematical Programs with Equilibrium Constraints. J Optim Theory Appl (2024). https://doi.org/10.1007/s10957-024-02475-6
Download citation
Received : 19 September 2023
Accepted : 05 June 2024
Published : 01 July 2024
DOI : https://doi.org/10.1007/s10957-024-02475-6
Share this article
Anyone you share the following link with will be able to read this content:
Sorry, a shareable link is not currently available for this article.
Provided by the Springer Nature SharedIt content-sharing initiative
- Mathematical program with equilibrium constraints
- Nonconvex optimization
- Non-Lipschitz continuity
- Sparsity-inducing penalty
- Smoothing function
- Regularization method
Mathematics Subject Classification
- Find a journal
- Publish with us
- Track your research

IMAGES
VIDEO
COMMENTS
Luckily there are many numerical methods for solving constrained optimization problems, though we will not discuss them here. This page titled 2.7: Constrained Optimization - Lagrange Multipliers is shared under a GNU Free Documentation License 1.3 license and was authored, remixed, and/or curated by Michael Corral via source content that was ...
The constrained-optimization problem (COP) is a significant generalization of the classic constraint-satisfaction problem (CSP) ... Virtually, this corresponds on ignoring the evaluated variables and solving the problem on the unassigned ones, except that the latter problem has already been solved. More precisely, the cost of soft constraints ...
1. Introduction. Constrained optimization, also known as constraint optimization, is the process of optimizing an objective function with respect to a set of decision variables while imposing constraints on those variables. In this tutorial, we'll provide a brief introduction to constrained optimization, explore some examples, and introduce ...
However, solving constrained optimization problems is a very important topic in applied mathematics. The techniques developed here are the basis for solving larger problems, where more than two variables are involved. We illustrate the technique again with a classic problem.
The "Lagrange multipliers" technique is a way to solve constrained optimization problems. Super useful! Background. Contour maps; ... However, if you (or more realistically a computer) were solving a given constrained optimization problem, it's not like you would first find the unconstrained maximum, check if it fits the constraint, then turn ...
Constrained optimization introduction. The Lagrange multiplier technique is how we take advantage of the observation made in the last video, that the solution to a constrained optimization problem occurs when the contour lines of the function being maximized are tangent to the constraint curve. Created by Grant Sanderson.
Practice Problem 1 1. Write constraints for each of the following: a) A batch of cookies requires 3 cups of flour, and a cake requires 4. Write a constraint limiting the amount of cookies and cakes that can be made with 24 cups of flour. b) Box type 1 can hold 20 books and box type 2 can hold 12. Write a constraint for the number of boxes
If you find yourself solving a constrained optimization problem by hand, and you remember the idea of gradient alignment, feel free to go for it without worrying about the Lagrangian. In practice, it's often a computer solving these problems, not a human.
2 to get. solving this is using 1 = x21 + (2x2)2 4x1x2 wherep pt. e equality holds when x1 = 2x2.So x1 = 2=2 and x2 = 2=4.However, not all equality-constrained. We need general theory to solve constrained optimization problems with equal-ity constraints: mize f (x) subject t. h(x) = 0and the fe.
onA constrained optimization problem is a problem of the formmaximize (or minimi. (x, y) subject to the condition g(x, y) = 0.1From two to oneIn some cases one can solve for y as a func. ion of x and then find the extrema of a one variable function.That is, if the equation g(x, y) = 0 is equivalent to y = h(x), then we may set f(x) = F (x, h(x)) a.
maximize L, once has been chosen. This provides an intuition into this method of solving the constrained maximization problem. In the constrained problem we have told the decision maker that she must satisfy g(x 1;:::;x n) = c and that she should choose among all points that satisfy this constraint the point at which f(x 1;:::;x n) is greatest ...
Optimization III: Constrained Optimization. Really Di cult! \Maximize pro ts where you make a positive amount of each product and use limited material." A feasible point is any point ~x satisfying g(~x) = ~ 0 and h(~x) ~ 0: The feasible set is the set of all points ~x satisfying these constraints. A feasible point is any point ~x satisfying g ...
It follows from this that we can solve constrained optimization problems with equality constraints as follows (assuming ∇ᵤg(u*)≠0): ... this method of Lagrange multipliers is powerful in that it casts a constrained optimization problem into an unconstrained optimization problem which we can solve by simply setting the gradient as zero.
Theorem 5.1 Suppose that f(x) is twice differentiable on the open convex set S. Then f(x) is a convex function on the domain S if and only if H(x) is SPSD for all x S. ∈. The following functions are examples of convex functions in n-dimensions. f(x) = aT x + b. f(x) = 1xT Mx cT x where M is SPSD. 2 −. f(x) = x.
Constrained optimization problems are problems for which a function f(x) is to be minimized or maximized subject to constraints \[CapitalPhi] (x). Here f:\[DoubleStruckCapitalR]^n-> \[DoubleStruckCapitalR] is called the objective function and \[CapitalPhi](x) is a Boolean-valued formula. ... Solving Optimization Problems. The methods used to ...
Constrained Optimization Definition. Constrained minimization is the problem of finding a vector x that is a local minimum to a scalar function f ( x ) subject to constraints on the allowable x: min x f ( x) such that one or more of the following holds: c(x) ≤ 0, ceq(x) = 0, A·x ≤ b, Aeq·x = beq, l ≤ x ≤ u. There are even more ...
Photo by Drew Dizzy Graham on Unsplash. Interior Point Methods typically solve the constrained convex optimization problem by applying Newton Method to a sequence of equality constrained problems. Barrier methods, as the name suggest, employ barrier functions to integrate inequality constraints into the objective function. Since we want to merge inequality constraints to the objective, the ...
Lagrange multipliers, using tangency to solve constrained optimization. The Lagrange multiplier technique is how we take advantage of the observation made in the last video, that the solution to a constrained optimization problem occurs when the contour lines of the function being maximized are tangent to the constraint curve.
Constrained Optimization and Lagrange Multipliers. In Preview Activity 10.8.1, we considered an optimization problem where there is an external constraint on the variables, namely that the girth plus the length of the package cannot exceed 108 inches. We saw that we can create a function g from the constraint, specifically g(x, y) = 4x + y.
Solving problem using fmincon. Local minimum found that satisfies the constraints. Optimization completed because the objective function is non-decreasing in feasible directions, to within the value of the optimality tolerance, and constraints are satisfied to within the value of the constraint tolerance.
The commonly used mathematical technique of constrained optimizations involves the use of Lagrange multiplier and Lagrange function to solve these problems followed by checking the second order conditions using the Bordered Hessian. When the objective function is a function of two variables, and there is only one equality constraint, the ...
Constrained Optimization. Added Mar 16, 2017 by vik_31415 in Mathematics. Constrained Optimization. Send feedback | Visit Wolfram|Alpha. Get the free "Constrained Optimization" widget for your website, blog, Wordpress, Blogger, or iGoogle. Find more Mathematics widgets in Wolfram|Alpha.
Create an optimization problem named prob having obj as the objective function. prob = optimproblem( 'Objective' ,obj); Create the nonlinear constraint as a polynomial of the optimization variable. nlcons = x(1)^2 + x(2)^2 <= 1; Include the nonlinear constraint in the problem. prob.Constraints.circlecons = nlcons;
In recent years, the Cuckoo Optimization Algorithm (COA) has been widely used to solve various optimization problems due to its simplicity, efficacy, and capability to avoid getting trapped in local optima. However, COA has some limitations such as low convergence when it comes to solving constrained optimization problems with many constraints.
With the convex and smooth objective satisfying locally Lipschitz gradient we obtain the complexity O ( 1 k ) of f ( x k ) − f ⁎ at most. By using the idea of the new stepsize, we propose another new algorithm based on the projected gradient for solving a class of nonconvex optimization problems over a closed convex set.
Non-convex functional constrained optimization problems have gained substantial attention in machine learning and signal processing. This paper develops a new primal-dual algorithm for solving this class of problems. The algorithm is based on a novel form of the Lagrangian function, termed {\\em Proximal-Perturbed Augmented Lagrangian}, which enables us to develop an efficient and simple first ...
For any \(t \ne 0\), we let \(\textrm{sign}(t) = 1\) if \(t > 0\) and \(\textrm{sign}(t) = -1\) otherwise.. Problem is a nonconvex problem and it is necessary to investigate the convergence to its stationary points.For optimization problems with locally Lipschitz functions, a CQ such as the popular linear independence constraint qualification is required to ensure that local minimizers are KKT ...