| ( 112 m/s) 2 = (0 m/s) 2 + 2*(a)*(398 m) 12544 m 2 /s 2 = 0 m 2 /s 2 + (796 m)*a 12544 m 2 /s 2 = (796 m)*a (12544 m 2 /s 2 )/(796 m) = a a = 15.8 m/s 2 Return to Problem 19 v f 2 = v i 2 + 2*a*d (0 m/s) 2 = v i 2 + 2*(-9.8 m/s 2 )*(91.5 m) 0 m 2 /s 2 = v i 2 - 1793 m 2 /s 2 1793 m 2 /s 2 = v i 2 v i = 42.3 m/s Now convert from m/s to mi/hr: v i = 42.3 m/s * (2.23 mi/hr)/(1 m/s) v i = 94.4 mi/hr Return to Problem 20 - Publications
- Conferences & Events
- Professional Learning
- Science Standards
- Awards & Competitions
- Instructional Materials
- Free Resources
- American Rescue Plan
- For Preservice Teachers
- NCCSTS Case Collection
- Science and STEM Education Jobs
- Interactive eBooks+
- Digital Catalog
- Regional Product Representatives
- e-Newsletters
- Bestselling Books
- Latest Books
- Popular Book Series
- Submit Book Proposal
- Web Seminars
- National Conference • New Orleans 24
- Leaders Institute • New Orleans 24
- Exhibits & Sponsorship
- Submit a Proposal
- Conference Reviewers
- Past Conferences
- Latest Resources
- Professional Learning Units & Courses
- For Districts
- Online Course Providers
- Schools & Districts
- College Professors & Students
- The Standards
- Teachers and Admin
- eCYBERMISSION
- Toshiba/NSTA ExploraVision
- Junior Science & Humanities Symposium
- Teaching Awards
- Climate Change
- Earth & Space Science
- New Science Teachers
- Early Childhood
- Middle School
- High School
- Postsecondary
- Informal Education
- Journal Articles
- Lesson Plans
- e-newsletters
- Science & Children
- Science Scope
- The Science Teacher
- Journal of College Sci. Teaching
- Connected Science Learning
- NSTA Reports
- Next-Gen Navigator
- Science Update
- Teacher Tip Tuesday
- Trans. Sci. Learning
MyNSTA CommunityA Problem-Solving ExperimentUsing Beer’s Law to Find the Concentration of Tartrazine The Science Teacher—January/February 2022 (Volume 89, Issue 3) By Kevin Mason, Steve Schieffer, Tara Rose, and Greg Matthias Share Start a Discussion  A problem-solving experiment is a learning activity that uses experimental design to solve an authentic problem. It combines two evidence-based teaching strategies: problem-based learning and inquiry-based learning. The use of problem-based learning and scientific inquiry as an effective pedagogical tool in the science classroom has been well established and strongly supported by research ( Akinoglu and Tandogan 2007 ; Areepattamannil 2012 ; Furtak, Seidel, and Iverson 2012 ; Inel and Balim 2010 ; Merritt et al. 2017 ; Panasan and Nuangchalerm 2010 ; Wilson, Taylor, and Kowalski 2010 ). Floyd James Rutherford, the founder of the American Association for the Advancement of Science (AAAS) Project 2061 once stated, “To separate conceptually scientific content from scientific inquiry,” he underscored, “is to make it highly probable that the student will properly understand neither” (1964, p. 84). A more recent study using randomized control trials showed that teachers that used an inquiry and problem-based pedagogy for seven months improved student performance in math and science ( Bando, Nashlund-Hadley, and Gertler 2019 ). A problem-solving experiment uses problem-based learning by posing an authentic or meaningful problem for students to solve and inquiry-based learning by requiring students to design an experiment to collect and analyze data to solve the problem. In the problem-solving experiment described in this article, students used Beer’s Law to collect and analyze data to determine if a person consumed a hazardous amount of tartrazine (Yellow Dye #5) for their body weight. The students used their knowledge of solutions, molarity, dilutions, and Beer’s Law to design their own experiment and calculate the amount of tartrazine in a yellow sports drink (or citrus-flavored soda). According to the Next Generation Science Standards, energy is defined as “a quantitative property of a system that depends on the motion and interactions of matter and radiation with that system” ( NGSS Lead States 2013 ). Interactions of matter and radiation can be some of the most challenging for students to observe, investigate, and conceptually understand. As a result, students need opportunities to observe and investigate the interactions of matter and radiation. Light is one example of radiation that interacts with matter. Light is electromagnetic radiation that is detectable to the human eye and exhibits properties of both a wave and a particle. When light interacts with matter, light can be reflected at the surface, absorbed by the matter, or transmitted through the matter ( Figure 1 ). When a single beam of light enters a substance at a perpendicularly (at a 90 ° angle to the surface), the amount of reflection is minimal. Therefore, the light will either be absorbed by the substance or be transmitted through the substance. When a given wavelength of light shines into a solution, the amount of light that is absorbed will depend on the identity of the substance, the thickness of the container, and the concentration of the solution. 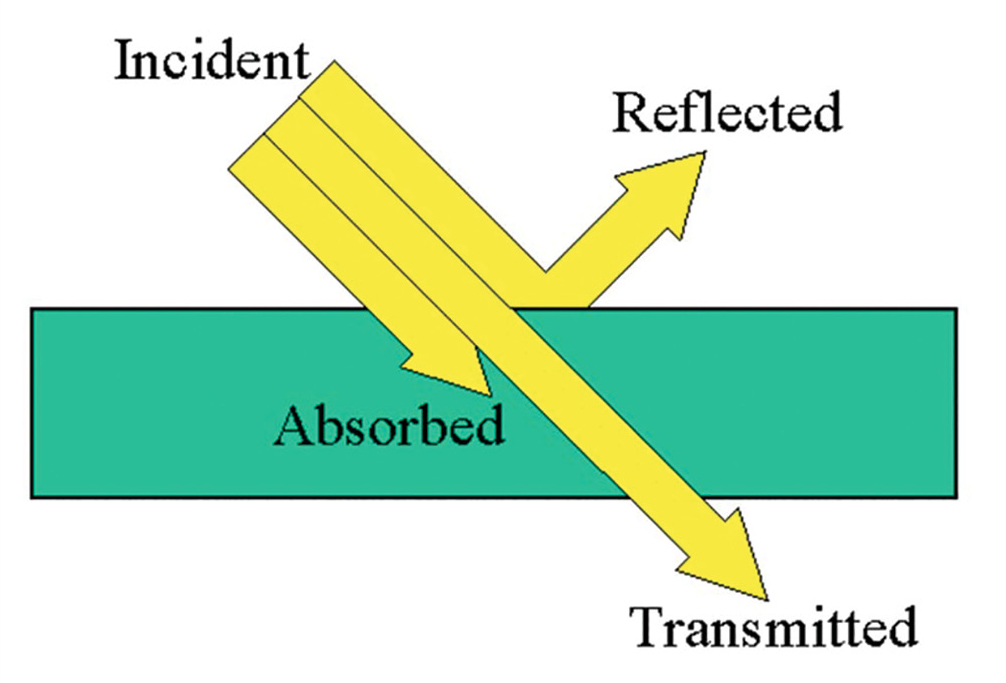 Light interacting with matter. (Retrieved from https://etorgerson.files.wordpress.com/2011/05/light-reflect-refract-absorb-label.jpg ). Beer’s Law states the amount of light absorbed is directly proportional to the thickness and concentration of a solution. Beer’s Law is also sometimes known as the Beer-Lambert Law. A solution of a higher concentration will absorb more light and transmit less light ( Figure 2 ). Similarly, if the solution is placed in a thicker container that requires the light to pass through a greater distance, then the solution will absorb more light and transmit less light. 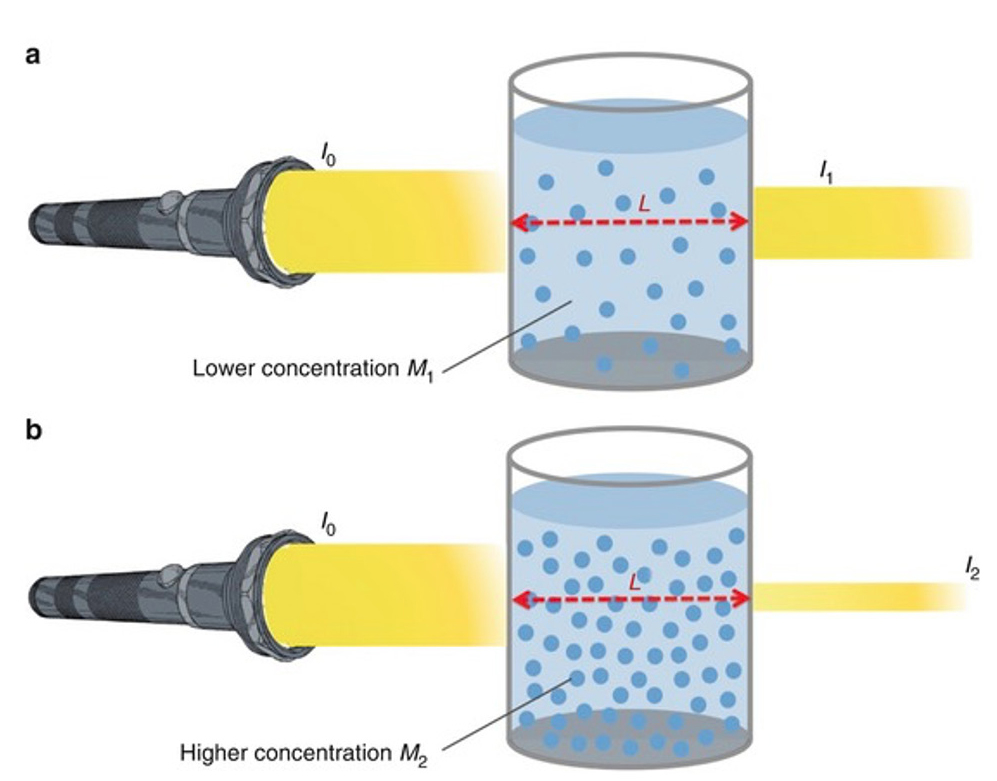 Light transmitted through a solution. (Retrieved from https://media.springernature.com/original/springer-static/image/chp%3A10.1007%2F978-3-319-57330-4_13/MediaObjects/432946_1_En_13_Fig4_HTML.jpg ). Definitions of key terms. Absorbance (A) – the process of light energy being captured by a substance Beer’s Law (Beer-Lambert Law) – the absorbance (A) of light is directly proportional to the molar absorptivity (ε), thickness (b), and concentration (C) of the solution (A = εbC) Concentration (C) – the amount of solute dissolved per amount of solution Cuvette – a container used to hold a sample to be tested in a spectrophotometer Energy (E) – a quantitative property of a system that depends on motion and interactions of matter and radiation with that system (NGSS Lead States 2013). Intensity (I) – the amount or brightness of light Light – electromagnetic radiation that is detectable to the human eye and exhibits properties of both a wave and a particle Molar Absorptivity (ε) – a property that represents the amount of light absorbed by a given substance per molarity of the solution and per centimeter of thickness (M-1 cm-1) Molarity (M) – the number of moles of solute per liters of solution (Mol/L) Reflection – the process of light energy bouncing off the surface of a substance Spectrophotometer – a device used to measure the absorbance of light by a substance Tartrazine – widely used food and liquid dye Transmittance (T) – the process of light energy passing through a substance The amount of light absorbed by a solution can be measured using a spectrophotometer. The solution of a given concentration is placed in a small container called a cuvette. The cuvette has a known thickness that can be held constant during the experiment. It is also possible to obtain cuvettes of different thicknesses to study the effect of thickness on the absorption of light. The key definitions of the terms related to Beer’s Law and the learning activity presented in this article are provided in Figure 3 . Overview of the problem-solving experimentIn the problem presented to students, a 140-pound athlete drinks two bottles of yellow sports drink every day ( Figure 4 ; see Online Connections). When she starts to notice a rash on her skin, she reads the label of the sports drink and notices that it contains a yellow dye known as tartrazine. While tartrazine is safe to drink, it may produce some potential side effects in large amounts, including rashes, hives, or swelling. The students must design an experiment to determine the concentration of tartrazine in the yellow sports drink and the number of milligrams of tartrazine in two bottles of the sports drink. While a sports drink may have many ingredients, the vast majority of ingredients—such as sugar or electrolytes—are colorless when dissolved in water solution. The dyes added to the sports drink are responsible for the color of the sports drink. Food manufacturers may use different dyes to color sports drinks to the desired color. Red dye #40 (allura red), blue dye #1 (brilliant blue), yellow dye #5 (tartrazine), and yellow dye #6 (sunset yellow) are the four most common dyes or colorants in sports drinks and many other commercial food products ( Stevens et al. 2015 ). The concentration of the dye in the sports drink affects the amount of light absorbed. In this problem-solving experiment, the students used the previously studied concept of Beer’s Law—using serial dilutions and absorbance—to find the concentration (molarity) of tartrazine in the sports drink. Based on the evidence, the students then determined if the person had exceeded the maximum recommended daily allowance of tartrazine, given in mg/kg of body mass. The learning targets for this problem-solving experiment are shown in Figure 5 (see Online Connections). Pre-laboratory experiencesA problem-solving experiment is a form of guided inquiry, which will generally require some prerequisite knowledge and experience. In this activity, the students needed prior knowledge and experience with Beer’s Law and the techniques in using Beer’s Law to determine an unknown concentration. Prior to the activity, students learned how Beer’s Law is used to relate absorbance to concentration as well as how to use the equation M 1 V 1 = M 2 V 2 to determine concentrations of dilutions. The students had a general understanding of molarity and using dimensional analysis to change units in measurements. The techniques for using Beer’s Law were introduced in part through a laboratory experiment using various concentrations of copper sulfate. A known concentration of copper sulfate was provided and the students followed a procedure to prepare dilutions. Students learned the technique for choosing the wavelength that provided the maximum absorbance for the solution to be tested ( λ max ), which is important for Beer’s Law to create a linear relationship between absorbance and solution concentration. Students graphed the absorbance of each concentration in a spreadsheet as a scatterplot and added a linear trend line. Through class discussion, the teacher checked for understanding in using the equation of the line to determine the concentration of an unknown copper sulfate solution. After the students graphed the data, they discussed how the R2 value related to the data set used to construct the graph. After completing this experiment, the students were comfortable making dilutions from a stock solution, calculating concentrations, and using the spectrophotometer to use Beer’s Law to determine an unknown concentration. Introducing the problemAfter the initial experiment on Beer’s Law, the problem-solving experiment was introduced. The problem presented to students is shown in Figure 4 (see Online Connections). A problem-solving experiment provides students with a valuable opportunity to collaborate with other students in designing an experiment and solving a problem. For this activity, the students were assigned to heterogeneous or mixed-ability laboratory groups. Groups should be diversified based on gender; research has shown that gender diversity among groups improves academic performance, while racial diversity has no significant effect ( Hansen, Owan, and Pan 2015 ). It is also important to support students with special needs when assigning groups. The mixed-ability groups were assigned intentionally to place students with special needs with a peer who has the academic ability and disposition to provide support. In addition, some students may need additional accommodations or modifications for this learning activity, such as an outlined lab report, a shortened lab report format, or extended time to complete the analysis. All students were required to wear chemical-splash goggles and gloves, and use caution when handling solutions and glass apparatuses. Designing the experimentDuring this activity, students worked in lab groups to design their own experiment to solve a problem. The teacher used small-group and whole-class discussions to help students understand the problem. Students discussed what information was provided and what they need to know and do to solve the problem. In planning the experiment, the teacher did not provide a procedure and intentionally provided only minimal support to the students as needed. The students designed their own experimental procedure, which encouraged critical thinking and problem solving. The students needed to be allowed to struggle to some extent. The teacher provided some direction and guidance by posing questions for students to consider and answer for themselves. Students were also frequently reminded to review their notes and the previous experiment on Beer’s Law to help them better use their resources to solve the problem. The use of heterogeneous or mixed-ability groups also helped each group be more self-sufficient and successful in designing and conducting the experiment. Students created a procedure for their experiment with the teacher providing suggestions or posing questions to enhance the experimental design, if needed. Safety was addressed during this consultation to correct safety concerns in the experimental design or provide safety precautions for the experiment. Students needed to wear splash-proof goggles and gloves throughout the experiment. In a few cases, students realized some opportunities to improve their experimental design during the experiment. This was allowed with the teacher’s approval, and the changes to the procedure were documented for the final lab report. Conducting the experimentA sample of the sports drink and a stock solution of 0.01 M stock solution of tartrazine were provided to the students. There are many choices of sports drinks available, but it is recommended that the ingredients are checked to verify that tartrazine (yellow dye #5) is the only colorant added. This will prevent other colorants from affecting the spectroscopy results in the experiment. A citrus-flavored soda could also be used as an alternative because many sodas have tartrazine added as well. It is important to note that tartrazine is considered safe to drink, but it may produce some potential side effects in large amounts, including rashes, hives, or swelling. A list of the materials needed for this problem-solving experiment is shown in Figure 6 (see Online Connections). This problem-solving experiment required students to create dilutions of known concentrations of tartrazine as a reference to determine the unknown concentration of tartrazine in a sports drink. To create the dilutions, the students were provided with a 0.01 M stock solution of tartrazine. The teacher purchased powdered tartrazine, available from numerous vendors, to create the stock solution. The 0.01 M stock solution was prepared by weighing 0.534 g of tartrazine and dissolving it in enough distilled water to make a 100 ml solution. Yellow food coloring could be used as an alternative, but it would take some research to determine its concentration. Since students have previously explored the experimental techniques, they should know to prepare dilutions that are somewhat darker and somewhat lighter in color than the yellow sports drink sample. Students should use five dilutions for best results. Typically, a good range for the yellow sports drink is standard dilutions ranging from 1 × 10-3 M to 1 × 10-5 M. The teacher may need to caution the students that if a dilution is too dark, it will not yield good results and lower the R2 value. Students that used very dark dilutions often realized that eliminating that data point created a better linear trendline, as long as it didn’t reduce the number of data points to fewer than four data points. Some students even tried to use the 0.01 M stock solution without any dilution. This was much too dark. The students needed to do substantial dilutions to get the solutions in the range of the sports drink. After the dilutions are created, the absorbance of each dilution was measured using a spectrophotometer. A Vernier SpectroVis (~$400) spectrophotometer was used to measure the absorbance of the prepared dilutions with known concentrations. The students adjusted the spectrophotometer to use different wavelengths of light and selected the wavelength with the highest absorbance reading. The same wavelength was then used for each measurement of absorbance. A wavelength of 650 nanometers (nm) provided an accurate measurement and good linear relationship. After measuring the absorbance of the dilutions of known concentrations, the students measured the absorbance of the sports drink with an unknown concentration of tartrazine using the spectrophotometer at the same wavelength. If a spectrophotometer is not available, a color comparison can be used as a low-cost alternative for completing this problem-solving experiment ( Figure 7 ; see Online Connections). Analyzing the resultsAfter completing the experiment, the students graphed the absorbance and known tartrazine concentrations of the dilutions on a scatter-plot to create a linear trendline. In this experiment, absorbance was the dependent variable, which should be graphed on the y -axis. Some students mistakenly reversed the axes on the scatter-plot. Next, the students used the graph to find the equation for the line. Then, the students solve for the unknown concentration (molarity) of tartrazine in the sports drink given the linear equation and the absorbance of the sports drink measured experimentally. To answer the question posed in the problem, the students also calculated the maximum amount of tartrazine that could be safely consumed by a 140 lb. person, using the information given in the problem. A common error in solving the problem was not converting the units of volume given in the problem from ounces to liters. With the molarity and volume in liters, the students then calculated the mass of tartrazine consumed per day in milligrams. A sample of the graph and calculations from one student group are shown in Figure 8 . Finally, based on their calculations, the students answered the question posed in the original problem and determined if the person’s daily consumption of tartrazine exceeded the threshold for safe consumption. In this case, the students concluded that the person did NOT consume more than the allowable daily limit of tartrazine. 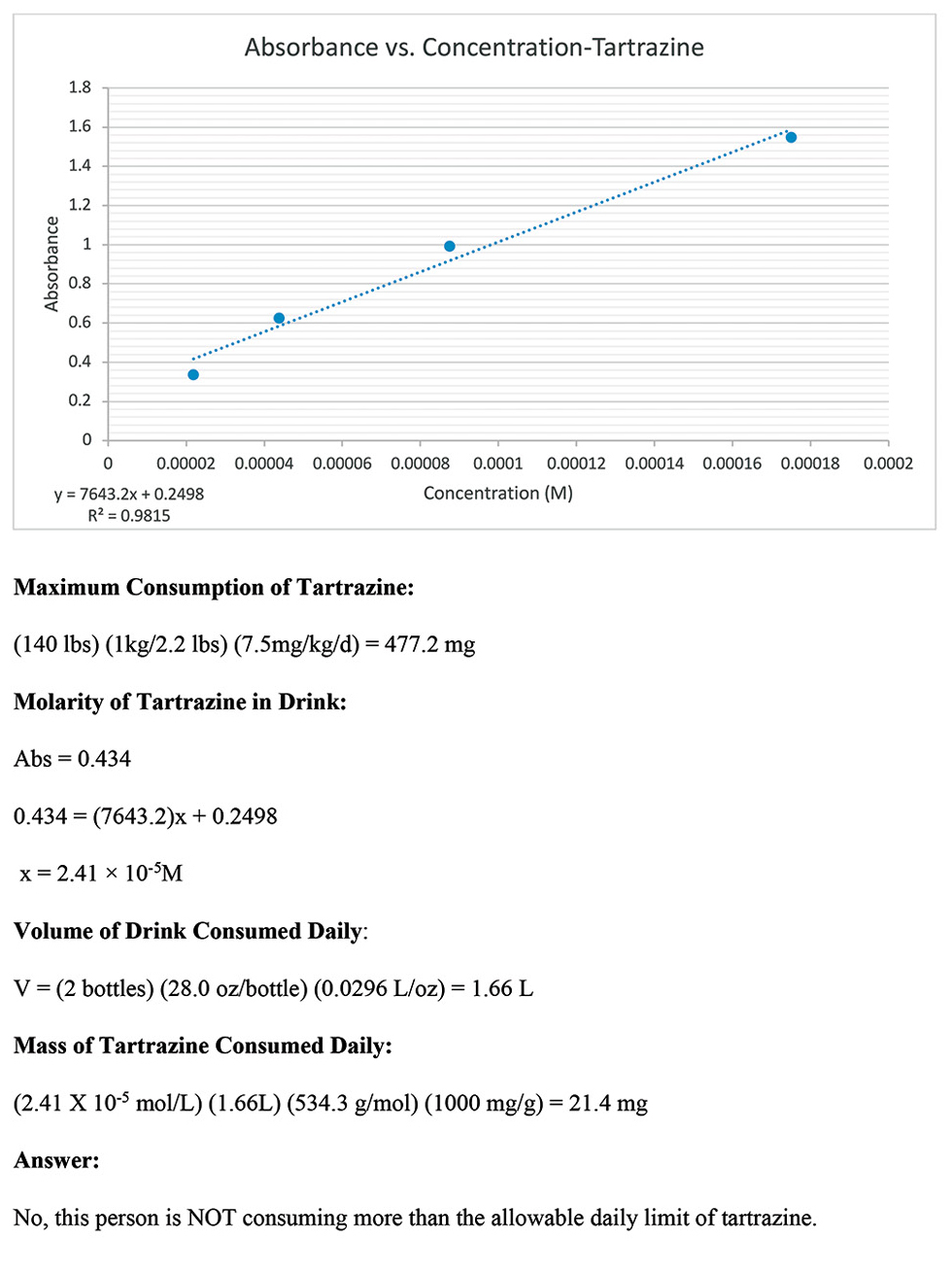 Sample graph and calculations from a student group. Communicating the resultsAfter conducting the experiment, students reported their results in a written laboratory report that included the following sections: title, purpose, introduction, hypothesis, materials and methods, data and calculations, conclusion, and discussion. The laboratory report was assessed using the scoring rubric shown in Figure 9 (see Online Connections). In general, the students did very well on this problem-solving experiment. Students typically scored a three or higher on each criteria of the rubric. Throughout the activity, the students successfully demonstrated their ability to design an experiment, collect data, perform calculations, solve a problem, and effectively communicate those results. This activity is authentic problem-based learning in science as the true concentration of tartrazine in the sports drink was not provided by the teacher or known by the students. The students were generally somewhat biased as they assumed the experiment would result in exceeding the recommended maximum consumption of tartrazine. Some students struggled with reporting that the recommended limit was far higher than the two sports drinks consumed by the person each day. This allows for a great discussion about the use of scientific methods and evidence to provide unbiased answers to meaningful questions and problems. The most common errors in this problem-solving experiment were calculation errors, with the most common being calculating the concentrations of the dilutions (perhaps due to the use of very small concentrations). There were also several common errors in communicating the results in the laboratory report. In some cases, students did not provide enough background information in the introduction of the report. When the students communicated the results, some students also failed to reference specific data from the experiment. Finally, in the discussion section, some students expressed concern or doubts in the results, not because there was an obvious error, but because they did not believe the level consumed could be so much less than the recommended consumption limit of tartrazine. The scientific study and investigation of energy and matter are salient topics addressed in the Next Generation Science Standards ( Figure 10 ; see Online Connections). In a chemistry classroom, students should have multiple opportunities to observe and investigate the interaction of energy and matter. In this problem-solving experiment students used Beer’s Law to collect and analyze data to determine if a person consumed an amount of tartrazine that exceeded the maximum recommended daily allowance. The students correctly concluded that the person in the problem did not consume more than the recommended daily amount of tartrazine for their body weight. In this activity students learned to work collaboratively to design an experiment, collect and analyze data, and solve a problem. These skills extend beyond any one science subject or class. Through this activity, students had the opportunity to do real-world science to solve a problem without a previously known result. The process of designing an experiment may be difficult for some students that are often accustomed to being given an experimental procedure in their previous science classroom experiences. However, because students sometimes struggled to design their own experiment and perform the calculations, students also learned to persevere in collecting and analyzing data to solve a problem, which is a valuable life lesson for all students. ■ Online ConnectionsThe Beer-Lambert Law at Chemistry LibreTexts: https://bit.ly/3lNpPEi Beer’s Law – Theoretical Principles: https://teaching.shu.ac.uk/hwb/chemistry/tutorials/molspec/beers1.htm Beer’s Law at Illustrated Glossary of Organic Chemistry: http://www.chem.ucla.edu/~harding/IGOC/B/beers_law.html Beer Lambert Law at Edinburgh Instruments: https://www.edinst.com/blog/the-beer-lambert-law/ Beer’s Law Lab at PhET Interactive Simulations: https://phet.colorado.edu/en/simulation/beers-law-lab Figure 4. Problem-solving experiment problem statement: https://bit.ly/3pAYHtj Figure 5. Learning targets: https://bit.ly/307BHtb Figure 6. Materials list: https://bit.ly/308a57h Figure 7. The use of color comparison as a low-cost alternative: https://bit.ly/3du1uyO Figure 9. Summative performance-based assessment rubric: https://bit.ly/31KoZRj Figure 10. Connecting to the Next Generation Science Standards : https://bit.ly/3GlJnY0 Kevin Mason ( [email protected] ) is Professor of Education at the University of Wisconsin–Stout, Menomonie, WI; Steve Schieffer is a chemistry teacher at Amery High School, Amery, WI; Tara Rose is a chemistry teacher at Amery High School, Amery, WI; and Greg Matthias is Assistant Professor of Education at the University of Wisconsin–Stout, Menomonie, WI. Akinoglu, O., and R. Tandogan. 2007. The effects of problem-based active learning in science education on students’ academic achievement, attitude and concept learning. Eurasia Journal of Mathematics, Science, and Technology Education 3 (1): 77–81. Areepattamannil, S. 2012. Effects of inquiry-based science instruction on science achievement and interest in science: Evidence from Qatar. The Journal of Educational Research 105 (2): 134–146. Bando R., E. Nashlund-Hadley, and P. Gertler. 2019. Effect of inquiry and problem-based pedagogy on learning: Evidence from 10 field experiments in four countries. The National Bureau of Economic Research 26280. Furtak, E., T. Seidel, and H. Iverson. 2012. Experimental and quasi-experimental studies of inquiry-based science teaching: A meta-analysis. Review of Educational Research 82 (3): 300–329. Hansen, Z., H. Owan, and J. Pan. 2015. The impact of group diversity on class performance. Education Economics 23 (2): 238–258. Inel, D., and A. Balim. 2010. The effects of using problem-based learning in science and technology teaching upon students’ academic achievement and levels of structuring concepts. Pacific Forum on Science Learning and Teaching 11 (2): 1–23. Merritt, J., M. Lee, P. Rillero, and B. Kinach. 2017. Problem-based learning in K–8 mathematics and science education: A literature review. The Interdisciplinary Journal of Problem-based Learning 11 (2). NGSS Lead States. 2013. Next Generation Science Standards: For states, by states. Washington, DC: National Academies Press. Panasan, M., and P. Nuangchalerm. 2010. Learning outcomes of project-based and inquiry-based learning activities. Journal of Social Sciences 6 (2): 252–255. Rutherford, F.J. 1964. The role of inquiry in science teaching. Journal of Research in Science Teaching 2 (2): 80–84. Stevens, L.J., J.R. Burgess, M.A. Stochelski, and T. Kuczek. 2015. Amounts of artificial food dyes and added sugars in foods and sweets commonly consumed by children. Clinical Pediatrics 54 (4): 309–321. Wilson, C., J. Taylor, and S. Kowalski. 2010. The relative effects and equity of inquiry-based and commonplace science teaching on students’ knowledge, reasoning, and argumentation. Journal of Research in Science Teaching 47 (3): 276–301. Chemistry Crosscutting Concepts Curriculum Disciplinary Core Ideas General Science Inquiry Instructional Materials Labs Lesson Plans Mathematics NGSS Pedagogy Science and Engineering Practices STEM Teaching Strategies Technology Three-Dimensional Learning High School You may also likeReports Article Journal Article Leadership Matters... Where do Goldy Muhammad’s Cultivating Genus Pursuits fit into science learning? In this article, 5th grade teachers are adding the pursuits into a F...  What is Problem Solving? (Steps, Techniques, Examples)By Status.net Editorial Team on May 7, 2023 — 5 minutes to read What Is Problem Solving?Definition and importance. Problem solving is the process of finding solutions to obstacles or challenges you encounter in your life or work. It is a crucial skill that allows you to tackle complex situations, adapt to changes, and overcome difficulties with ease. Mastering this ability will contribute to both your personal and professional growth, leading to more successful outcomes and better decision-making. Problem-Solving StepsThe problem-solving process typically includes the following steps: - Identify the issue : Recognize the problem that needs to be solved.
- Analyze the situation : Examine the issue in depth, gather all relevant information, and consider any limitations or constraints that may be present.
- Generate potential solutions : Brainstorm a list of possible solutions to the issue, without immediately judging or evaluating them.
- Evaluate options : Weigh the pros and cons of each potential solution, considering factors such as feasibility, effectiveness, and potential risks.
- Select the best solution : Choose the option that best addresses the problem and aligns with your objectives.
- Implement the solution : Put the selected solution into action and monitor the results to ensure it resolves the issue.
- Review and learn : Reflect on the problem-solving process, identify any improvements or adjustments that can be made, and apply these learnings to future situations.
Defining the ProblemTo start tackling a problem, first, identify and understand it. Analyzing the issue thoroughly helps to clarify its scope and nature. Ask questions to gather information and consider the problem from various angles. Some strategies to define the problem include: - Brainstorming with others
- Asking the 5 Ws and 1 H (Who, What, When, Where, Why, and How)
- Analyzing cause and effect
- Creating a problem statement
Generating SolutionsOnce the problem is clearly understood, brainstorm possible solutions. Think creatively and keep an open mind, as well as considering lessons from past experiences. Consider: - Creating a list of potential ideas to solve the problem
- Grouping and categorizing similar solutions
- Prioritizing potential solutions based on feasibility, cost, and resources required
- Involving others to share diverse opinions and inputs
Evaluating and Selecting SolutionsEvaluate each potential solution, weighing its pros and cons. To facilitate decision-making, use techniques such as: - SWOT analysis (Strengths, Weaknesses, Opportunities, Threats)
- Decision-making matrices
- Pros and cons lists
- Risk assessments
After evaluating, choose the most suitable solution based on effectiveness, cost, and time constraints. Implementing and Monitoring the SolutionImplement the chosen solution and monitor its progress. Key actions include: - Communicating the solution to relevant parties
- Setting timelines and milestones
- Assigning tasks and responsibilities
- Monitoring the solution and making adjustments as necessary
- Evaluating the effectiveness of the solution after implementation
Utilize feedback from stakeholders and consider potential improvements. Remember that problem-solving is an ongoing process that can always be refined and enhanced. Problem-Solving TechniquesDuring each step, you may find it helpful to utilize various problem-solving techniques, such as: - Brainstorming : A free-flowing, open-minded session where ideas are generated and listed without judgment, to encourage creativity and innovative thinking.
- Root cause analysis : A method that explores the underlying causes of a problem to find the most effective solution rather than addressing superficial symptoms.
- SWOT analysis : A tool used to evaluate the strengths, weaknesses, opportunities, and threats related to a problem or decision, providing a comprehensive view of the situation.
- Mind mapping : A visual technique that uses diagrams to organize and connect ideas, helping to identify patterns, relationships, and possible solutions.
BrainstormingWhen facing a problem, start by conducting a brainstorming session. Gather your team and encourage an open discussion where everyone contributes ideas, no matter how outlandish they may seem. This helps you: - Generate a diverse range of solutions
- Encourage all team members to participate
- Foster creative thinking
When brainstorming, remember to: - Reserve judgment until the session is over
- Encourage wild ideas
- Combine and improve upon ideas
Root Cause AnalysisFor effective problem-solving, identifying the root cause of the issue at hand is crucial. Try these methods: - 5 Whys : Ask “why” five times to get to the underlying cause.
- Fishbone Diagram : Create a diagram representing the problem and break it down into categories of potential causes.
- Pareto Analysis : Determine the few most significant causes underlying the majority of problems.
SWOT AnalysisSWOT analysis helps you examine the Strengths, Weaknesses, Opportunities, and Threats related to your problem. To perform a SWOT analysis: - List your problem’s strengths, such as relevant resources or strong partnerships.
- Identify its weaknesses, such as knowledge gaps or limited resources.
- Explore opportunities, like trends or new technologies, that could help solve the problem.
- Recognize potential threats, like competition or regulatory barriers.
SWOT analysis aids in understanding the internal and external factors affecting the problem, which can help guide your solution. Mind MappingA mind map is a visual representation of your problem and potential solutions. It enables you to organize information in a structured and intuitive manner. To create a mind map: - Write the problem in the center of a blank page.
- Draw branches from the central problem to related sub-problems or contributing factors.
- Add more branches to represent potential solutions or further ideas.
Mind mapping allows you to visually see connections between ideas and promotes creativity in problem-solving. Examples of Problem Solving in Various ContextsIn the business world, you might encounter problems related to finances, operations, or communication. Applying problem-solving skills in these situations could look like: - Identifying areas of improvement in your company’s financial performance and implementing cost-saving measures
- Resolving internal conflicts among team members by listening and understanding different perspectives, then proposing and negotiating solutions
- Streamlining a process for better productivity by removing redundancies, automating tasks, or re-allocating resources
In educational contexts, problem-solving can be seen in various aspects, such as: - Addressing a gap in students’ understanding by employing diverse teaching methods to cater to different learning styles
- Developing a strategy for successful time management to balance academic responsibilities and extracurricular activities
- Seeking resources and support to provide equal opportunities for learners with special needs or disabilities
Everyday life is full of challenges that require problem-solving skills. Some examples include: - Overcoming a personal obstacle, such as improving your fitness level, by establishing achievable goals, measuring progress, and adjusting your approach accordingly
- Navigating a new environment or city by researching your surroundings, asking for directions, or using technology like GPS to guide you
- Dealing with a sudden change, like a change in your work schedule, by assessing the situation, identifying potential impacts, and adapting your plans to accommodate the change.
- How to Resolve Employee Conflict at Work [Steps, Tips, Examples]
- How to Write Inspiring Core Values? 5 Steps with Examples
- 30 Employee Feedback Examples (Positive & Negative)
 ChatGPT for TeachersTrauma-informed practices in schools, teacher well-being, cultivating diversity, equity, & inclusion, integrating technology in the classroom, social-emotional development, covid-19 resources, invest in resilience: summer toolkit, civics & resilience, all toolkits, degree programs, trauma-informed professional development, teacher licensure & certification, how to become - career information, classroom management, instructional design, lifestyle & self-care, online higher ed teaching, current events, stem projects that tackle real-world problems.  STEM learning is largely about designing creative solutions for real-world problems. When students learn within the context of authentic, problem-based STEM design, they can more clearly see the genuine impact of their learning. That kind of authenticity builds engagement, taking students from groans of “When will I ever use this?” to a genuine connection between skills and application. Using STEM to promote critical thinking and innovation“Educational outcomes in traditional settings focus on how many answers a student knows. We want students to learn how to develop a critical stance with their work: inquiring, editing, thinking flexibly, and learning from another person’s perspective,” says Arthur L. Costa in his book Learning and Leading with Habits of Mind . “The critical attribute of intelligent human beings is not only having information but also knowing how to act on it.” Invention and problem-solving aren’t just for laboratory thinkers hunkered down away from the classroom. Students from elementary to high school can wonder, design, and invent a real product that solves real problems. “ Problem-solving involves finding answers to questions and solutions for undesired effects. STEM lessons revolve around the engineering design process (EDP) — an organized, open-ended approach to investigation that promotes creativity, invention, and prototype design, along with testing and analysis,” says Ann Jolly in her book STEM by Design . “These iterative steps will involve your students in asking critical questions about the problem, and guide them through creating and testing actual prototypes to solve that problem.” STEM projects that use real-world problemsHere are some engaging projects that get your students thinking about how to solve real-world problems. Preventing soil erosionIn this project, meant for sixth – 12th grade, students learn to build a seawall to protest a coastline from erosion, calculating wave energy to determine the best materials for the job. See the project. Growing food during a floodA natural disaster that often devastates communities, floods can make it difficult to grow food. In this project, students explore “a problem faced by farmers in Bangladesh and how to grow food even when the land floods.” See the project . Solving a city’s design needsGet your middle or high school students involved in some urban planning. Students can identify a city’s issues, relating to things like transportation, the environment, or overcrowding — and design solutions. See the project here or this Lego version for younger learners. Creating clean waterToo many areas of the world — including cities in our own country — do not have access to clean water. In this STEM project, teens will learn how to build and test their own water filtration systems. See the project here . Improving the lives of those with disabilitiesHow can someone with crutches or a wheelchair carry what they need? Through some crafty designs! This project encourages middle school students to think creatively and to participate in civic engagement. See the project here . Cleaning up an oil spillWe’ve all seen images of beaches and wildlife covered in oil after a disastrous spill. This project gets elementary to middle school students designing and testing oil spill clean-up kits. See the project here . Building earthquake-resistant structuresWith the ever-increasing amount of devastating earthquakes around the world, this project solves some major problems. Elementary students can learn to create earthquake resistant structures in their classroom. See the project here . Constructing solar ovensIn remote places or impoverished areas, it’s possible to make solar ovens to safely cook food. In this project, elementary students construct solar ovens to learn all about how they work and their environmental and societal impact. See the project here .  Stopping apple oxidizationStop those apples from turning brown with this oxidation-based project. Perfect for younger learners, students can predict, label, count, and experiment! See the project here . Advancing as a STEAM educatorThe push for STEM has evolved into the STEAM movement, adding the arts for further enrichment and engagement. There are so many ways to embed STEM or STEAM lessons in your curriculum, but doing it well requires foundational knowledge and professional development. Imagine what type of impact you could have on your students and your community if you were supported by a theoretical framework, a variety of strategies, and a wealth of ideas and resources. You may also like to read- Teaching STEM: Challenging Students to Think Through Tough Problems
- Professional Development Resources for STEM Teachers
- What is the Washington State STEM Lighthouse Program?
- Characteristics of a Great STEAM Program
- Building a Partnership Between Your School and a STEAM Organization
- The Art of Inquiry in STEAM Education
 Categorized as: Tips for Teachers and Classroom Resources Tagged as: Art , Educational Technology , Engaging Activities , Math and Science , Science , STEAM - Online & Campus Master's in Elementary Educat...
- 2020 Civics Engagement & Resilience: Tools fo...
- Online & Campus Master's in Curriculum Develo...
Change PasswordYour password must have 8 characters or more and contain 3 of the following:. - a lower case character,
- an upper case character,
- a special character
Password Changed SuccessfullyYour password has been changed Request UsernameCan't sign in? Forgot your username? Enter your email address below and we will send you your username If the address matches an existing account you will receive an email with instructions to retrieve your username Teaching Creativity and Inventive Problem Solving in ScienceDivision of Educational Studies, Emory University, Atlanta, GA 30322 Search for more papers by this author Engaging learners in the excitement of science, helping them discover the value of evidence-based reasoning and higher-order cognitive skills, and teaching them to become creative problem solvers have long been goals of science education reformers. But the means to achieve these goals, especially methods to promote creative thinking in scientific problem solving, have not become widely known or used. In this essay, I review the evidence that creativity is not a single hard-to-measure property. The creative process can be explained by reference to increasingly well-understood cognitive skills such as cognitive flexibility and inhibitory control that are widely distributed in the population. I explore the relationship between creativity and the higher-order cognitive skills, review assessment methods, and describe several instructional strategies for enhancing creative problem solving in the college classroom. Evidence suggests that instruction to support the development of creativity requires inquiry-based teaching that includes explicit strategies to promote cognitive flexibility. Students need to be repeatedly reminded and shown how to be creative, to integrate material across subject areas, to question their own assumptions, and to imagine other viewpoints and possibilities. Further research is required to determine whether college students' learning will be enhanced by these measures. INTRODUCTIONDr. Dunne paces in front of his section of first-year college students, today not as their Bio 110 teacher but in the role of facilitator in their monthly “invention session.” For this meeting, the topic is stem cell therapy in heart disease. Members of each team of four students have primed themselves on the topic by reading selected articles from accessible sources such as Science, Nature, and Scientific American, and searching the World Wide Web, triangulating for up-to-date, accurate, background information. Each team knows that their first goal is to define a set of problems or limitations to overcome within the topic and to begin to think of possible solutions. Dr. Dunne starts the conversation by reminding the group of the few ground rules: one speaker at a time, listen carefully and have respect for others' ideas, question your own and others' assumptions, focus on alternative paths or solutions, maintain an atmosphere of collaboration and mutual support. He then sparks the discussion by asking one of the teams to describe a problem in need of solution. Science in the United States is widely credited as a major source of discovery and economic development. According to the 2005 TAP Report produced by a prominent group of corporate leaders, “To maintain our country's competitiveness in the twenty-first century, we must cultivate the skilled scientists and engineers needed to create tomorrow's innovations.” ( www.tap2015.org/about/TAP_report2.pdf ). A panel of scientists, engineers, educators, and policy makers convened by the National Research Council (NRC) concurred with this view, reporting that the vitality of the nation “is derived in large part from the productivity of well-trained people and the steady stream of scientific and technical innovations they produce” ( NRC, 2007 ). For many decades, science education reformers have promoted the idea that learners should be engaged in the excitement of science; they should be helped to discover the value of evidence-based reasoning and higher-order cognitive skills, and be taught to become innovative problem solvers (for reviews, see DeHaan, 2005 ; Hake, 2005 ; Nelson, 2008 ; Perkins and Wieman, 2008 ). But the means to achieve these goals, especially methods to promote creative thinking in scientific problem solving, are not widely known or used. An invention session such as that led by the fictional Dr. Dunne, described above, may seem fanciful as a means of teaching students to think about science as something more than a body of facts and terms to memorize. In recent years, however, models for promoting creative problem solving were developed for classroom use, as detailed by Treffinger and Isaksen (2005) , and such techniques are often used in the real world of high technology. To promote imaginative thinking, the advertising executive Alex F. Osborn invented brainstorming ( Osborn, 1948 , 1979 ), a technique that has since been successful in stimulating inventiveness among engineers and scientists. Could such strategies be transferred to a class for college students? Could they serve as a supplement to a high-quality, scientific teaching curriculum that helps students learn the facts and conceptual frameworks of science and make progress along the novice–expert continuum? Could brainstorming or other instructional strategies that are specifically designed to promote creativity teach students to be more adaptive in their growing expertise, more innovative in their problem-solving abilities? To begin to answer those questions, we first need to understand what is meant by “creativity.” What Is Creativity? Big-C versus Mini-C CreativityHow to define creativity is an age-old question. Justice Potter Stewart's famous dictum regarding obscenity “I know it when I see it” has also long been an accepted test of creativity. But this is not an adequate criterion for developing an instructional approach. A scientist colleague of mine recently noted that “Many of us [in the scientific community] rarely give the creative process a second thought, imagining one either ‘has it’ or doesn't.” We often think of inventiveness or creativity in scientific fields as the kind of gift associated with a Michelangelo or Einstein. This is what Kaufman and Beghetto (2008) call big-C creativity, borrowing the term that earlier workers applied to the talents of experts in various fields who were identified as particularly creative by their expert colleagues ( MacKinnon, 1978 ). In this sense, creativity is seen as the ability of individuals to generate new ideas that contribute substantially to an intellectual domain. Howard Gardner defined such a creative person as one who “regularly solves problems, fashions products, or defines new questions in a domain in a way that is initially considered novel but that ultimately comes to be accepted in a particular cultural setting” ( Gardner, 1993 , p. 35). But there is another level of inventiveness termed by various authors as “little-c” ( Craft, 2000 ) or “mini-c” ( Kaufman and Beghetto, 2008 ) creativity that is widespread among all populations. This would be consistent with the workplace definition of creativity offered by Amabile and her coworkers: “coming up with fresh ideas for changing products, services and processes so as to better achieve the organization's goals” ( Amabile et al. , 2005 ). Mini-c creativity is based on what Craft calls “possibility thinking” ( Craft, 2000 , pp. 3–4), as experienced when a worker suddenly has the insight to visualize a new, improved way to accomplish a task; it is represented by the “aha” moment when a student first sees two previously disparate concepts or facts in a new relationship, an example of what Arthur Koestler identified as bisociation: “perceiving a situation or event in two habitually incompatible associative contexts” ( Koestler, 1964 , p. 95). In this essay, I maintain that mini-c creativity is not a mysterious, innate endowment of rare individuals. Instead, I argue that creative thinking is a multicomponent process, mediated through social interactions, that can be explained by reference to increasingly well-understood mental abilities such as cognitive flexibility and cognitive control that are widely distributed in the population. Moreover, I explore some of the recent research evidence (though with no effort at a comprehensive literature review) showing that these mental abilities are teachable; like other higher-order cognitive skills (HOCS), they can be enhanced by explicit instruction. Creativity Is a Multicomponent ProcessEfforts to define creativity in psychological terms go back to J. P. Guilford ( Guilford, 1950 ) and E. P. Torrance ( Torrance, 1974 ), both of whom recognized that underlying the construct were other cognitive variables such as ideational fluency, originality of ideas, and sensitivity to missing elements. Many authors since then have extended the argument that a creative act is not a singular event but a process, an interplay among several interactive cognitive and affective elements. In this view, the creative act has two phases, a generative and an exploratory or evaluative phase ( Finke et al. , 1996 ). During the generative process, the creative mind pictures a set of novel mental models as potential solutions to a problem. In the exploratory phase, we evaluate the multiple options and select the best one. Early scholars of creativity, such as J. P. Guilford, characterized the two phases as divergent thinking and convergent thinking ( Guilford, 1950 ). Guilford defined divergent thinking as the ability to produce a broad range of associations to a given stimulus or to arrive at many solutions to a problem (for overviews of the field from different perspectives, see Amabile, 1996 ; Banaji et al. , 2006 ; Sawyer, 2006 ). In neurocognitive terms, divergent thinking is referred to as associative richness ( Gabora, 2002 ; Simonton, 2004 ), which is often measured experimentally by comparing the number of words that an individual generates from memory in response to stimulus words on a word association test. In contrast, convergent thinking refers to the capacity to quickly focus on the one best solution to a problem. The idea that there are two stages to the creative process is consistent with results from cognition research indicating that there are two distinct modes of thought, associative and analytical ( Neisser, 1963 ; Sloman, 1996 ). In the associative mode, thinking is defocused, suggestive, and intuitive, revealing remote or subtle connections between items that may be correlated, or may not, and are usually not causally related ( Burton, 2008 ). In the analytical mode, thought is focused and evaluative, more conducive to analyzing relationships of cause and effect (for a review of other cognitive aspects of creativity, see Runco, 2004 ). Science educators associate the analytical mode with the upper levels (analysis, synthesis, and evaluation) of Bloom's taxonomy (e.g., Crowe et al. , 2008 ), or with “critical thinking,” the process that underlies the “purposeful, self-regulatory judgment that drives problem-solving and decision-making” ( Quitadamo et al. , 2008 , p. 328). These modes of thinking are under cognitive control through the executive functions of the brain. The core executive functions, which are thought to underlie all planning, problem solving, and reasoning, are defined ( Blair and Razza, 2007 ) as working memory control (mentally holding and retrieving information), cognitive flexibility (considering multiple ideas and seeing different perspectives), and inhibitory control (resisting several thoughts or actions to focus on one). Readers wishing to delve further into the neuroscience of the creative process can refer to the cerebrocerebellar theory of creativity ( Vandervert et al. , 2007 ) in which these mental activities are described neurophysiologically as arising through interactions among different parts of the brain. The main point from all of these works is that creativity is not some single hard-to-measure property or act. There is ample evidence that the creative process requires both divergent and convergent thinking and that it can be explained by reference to increasingly well-understood underlying mental abilities ( Haring-Smith, 2006 ; Kim, 2006 ; Sawyer, 2006 ; Kaufman and Sternberg, 2007 ) and cognitive processes ( Simonton, 2004 ; Diamond et al. , 2007 ; Vandervert et al. , 2007 ). Creativity Is Widely Distributed and Occurs in a Social ContextAlthough it is understandable to speak of an aha moment as a creative act by the person who experiences it, authorities in the field have long recognized (e.g., Simonton, 1975 ) that creative thinking is not so much an individual trait but rather a social phenomenon involving interactions among people within their specific group or cultural settings. “Creativity isn't just a property of individuals, it is also a property of social groups” ( Sawyer, 2006 , p. 305). Indeed, Osborn introduced his brainstorming method because he was convinced that group creativity is always superior to individual creativity. He drew evidence for this conclusion from activities that demand collaborative output, for example, the improvisations of a jazz ensemble. Although each musician is individually creative during a performance, the novelty and inventiveness of each performer's playing is clearly influenced, and often enhanced, by “social and interactional processes” among the musicians ( Sawyer, 2006 , p. 120). Recently, Brophy (2006) offered evidence that for problem solving, the situation may be more nuanced. He confirmed that groups of interacting individuals were better at solving complex, multipart problems than single individuals. However, when dealing with certain kinds of single-issue problems, individual problem solvers produced a greater number of solutions than interacting groups, and those solutions were judged to be more original and useful. Consistent with the findings of Brophy (2006) , many scholars acknowledge that creative discoveries in the real world such as solving the problems of cutting-edge science—which are usually complex and multipart—are influenced or even stimulated by social interaction among experts. The common image of the lone scientist in the laboratory experiencing a flash of creative inspiration is probably a myth from earlier days. As a case in point, the science historian Mara Beller analyzed the social processes that underlay some of the major discoveries of early twentieth-century quantum physics. Close examination of successive drafts of publications by members of the Copenhagen group revealed a remarkable degree of influence and collaboration among 10 or more colleagues, although many of these papers were published under the name of a single author ( Beller, 1999 ). Sociologists Bruno Latour and Steve Woolgar's study ( Latour and Woolgar, 1986 ) of a neuroendocrinology laboratory at the Salk Institute for Biological Studies make the related point that social interactions among the participating scientists determined to a remarkable degree what discoveries were made and how they were interpreted. In the laboratory, researchers studied the chemical structure of substances released by the brain. By analysis of the Salk scientists' verbalizations of concepts, theories, formulas, and results of their investigations, Latour and Woolgar showed that the structures and interpretations that were agreed upon, that is, the discoveries announced by the laboratory, were mediated by social interactions and power relationships among members of the laboratory group. By studying the discovery process in other fields of the natural sciences, sociologists and anthropologists have provided more cases that further illustrate how social and cultural dimensions affect scientific insights (for a thoughtful review, see Knorr Cetina, 1995 ). In sum, when an individual experiences an aha moment that feels like a singular creative act, it may rather have resulted from a multicomponent process, under the influence of group interactions and social context. The process that led up to what may be sensed as a sudden insight will probably have included at least three diverse, but testable elements: 1) divergent thinking, including ideational fluency or cognitive flexibility, which is the cognitive executive function that underlies the ability to visualize and accept many ideas related to a problem; 2) convergent thinking or the application of inhibitory control to focus and mentally evaluate ideas; and 3) analogical thinking, the ability to understand a novel idea in terms of one that is already familiar. LITERATURE REVIEWWhat do we know about how to teach creativity. The possibility of teaching for creative problem solving gained credence in the 1960s with the studies of Jerome Bruner, who argued that children should be encouraged to “treat a task as a problem for which one invents an answer, rather than finding one out there in a book or on the blackboard” ( Bruner, 1965 , pp. 1013–1014). Since that time, educators and psychologists have devised programs of instruction designed to promote creativity and inventiveness in virtually every student population: pre–K, elementary, high school, and college, as well as in disadvantaged students, athletes, and students in a variety of specific disciplines (for review, see Scott et al. , 2004 ). Smith (1998) identified 172 instructional approaches that have been applied at one time or another to develop divergent thinking skills. Some of the most convincing evidence that elements of creativity can be enhanced by instruction comes from work with young children. Bodrova and Leong (2001) developed the Tools of the Mind (Tools) curriculum to improve all of the three core mental executive functions involved in creative problem solving: cognitive flexibility, working memory, and inhibitory control. In a year-long randomized study of 5-yr-olds from low-income families in 21 preschool classrooms, half of the teachers applied the districts' balanced literacy curriculum (literacy), whereas the experimenters trained the other half to teach the same academic content by using the Tools curriculum ( Diamond et al. , 2007 ). At the end of the year, when the children were tested with a battery of neurocognitive tests including a test for cognitive flexibility ( Durston et al. , 2003 ; Davidson et al. , 2006 ), those exposed to the Tools curriculum outperformed the literacy children by as much as 25% ( Diamond et al. , 2007 ). Although the Tools curriculum and literacy program were similar in academic content and in many other ways, they differed primarily in that Tools teachers spent 80% of their time explicitly reminding the children to think of alternative ways to solve a problem and building their executive function skills. Teaching older students to be innovative also demands instruction that explicitly promotes creativity but is rigorously content-rich as well. A large body of research on the differences between novice and expert cognition indicates that creative thinking requires at least a minimal level of expertise and fluency within a knowledge domain ( Bransford et al. , 2000 ; Crawford and Brophy, 2006 ). What distinguishes experts from novices, in addition to their deeper knowledge of the subject, is their recognition of patterns in information, their ability to see relationships among disparate facts and concepts, and their capacity for organizing content into conceptual frameworks or schemata ( Bransford et al. , 2000 ; Sawyer, 2005 ). Such expertise is often lacking in the traditional classroom. For students attempting to grapple with new subject matter, many kinds of problems that are presented in high school or college courses or that arise in the real world can be solved merely by applying newly learned algorithms or procedural knowledge. With practice, problem solving of this kind can become routine and is often considered to represent mastery of a subject, producing what Sternberg refers to as “pseudoexperts” ( Sternberg, 2003 ). But beyond such routine use of content knowledge the instructor's goal must be to produce students who have gained the HOCS needed to apply, analyze, synthesize, and evaluate knowledge ( Crowe et al. , 2008 ). The aim is to produce students who know enough about a field to grasp meaningful patterns of information, who can readily retrieve relevant knowledge from memory, and who can apply such knowledge effectively to novel problems. This condition is referred to as adaptive expertise ( Hatano and Ouro, 2003 ; Schwartz et al. , 2005 ). Instead of applying already mastered procedures, adaptive experts are able to draw on their knowledge to invent or adapt strategies for solving unique or novel problems within a knowledge domain. They are also able, ideally, to transfer conceptual frameworks and schemata from one domain to another (e.g., Schwartz et al. , 2005 ). Such flexible, innovative application of knowledge is what results in inventive or creative solutions to problems ( Crawford and Brophy, 2006 ; Crawford, 2007 ). Promoting Creative Problem Solving in the College ClassroomIn most college courses, instructors teach science primarily through lectures and textbooks that are dominated by facts and algorithmic processing rather than by concepts, principles, and evidence-based ways of thinking. This is despite ample evidence that many students gain little new knowledge from traditional lectures ( Hrepic et al. , 2007 ). Moreover, it is well documented that these methods engender passive learning rather than active engagement, boredom instead of intellectual excitement, and linear thinking rather than cognitive flexibility (e.g., Halpern and Hakel, 2003 ; Nelson, 2008 ; Perkins and Wieman, 2008 ). Cognitive flexibility, as noted, is one of the three core mental executive functions involved in creative problem solving ( Ausubel, 1963 , 2000 ). The capacity to apply ideas creatively in new contexts, referred to as the ability to “transfer” knowledge (see Mestre, 2005 ), requires that learners have opportunities to actively develop their own representations of information to convert it to a usable form. Especially when a knowledge domain is complex and fraught with ill-structured information, as in a typical introductory college biology course, instruction that emphasizes active-learning strategies is demonstrably more effective than traditional linear teaching in reducing failure rates and in promoting learning and transfer (e.g., Freeman et al. , 2007 ). Furthermore, there is already some evidence that inclusion of creativity training as part of a college curriculum can have positive effects. Hunsaker (2005) has reviewed a number of such studies. He cites work by McGregor (2001) , for example, showing that various creativity training programs including brainstorming and creative problem solving increase student scores on tests of creative-thinking abilities. Model creativity—students develop creativity when instructors model creative thinking and inventiveness. Repeatedly encourage idea generation—students need to be reminded to generate their own ideas and solutions in an environment free of criticism. Cross-fertilize ideas—where possible, avoid teaching in subject-area boxes: a math box, a social studies box, etc; students' creative ideas and insights often result from learning to integrate material across subject areas. Build self-efficacy—all students have the capacity to create and to experience the joy of having new ideas, but they must be helped to believe in their own capacity to be creative. Constantly question assumptions—make questioning a part of the daily classroom exchange; it is more important for students to learn what questions to ask and how to ask them than to learn the answers. Imagine other viewpoints—students broaden their perspectives by learning to reflect upon ideas and concepts from different points of view. How Is Creativity Related to Critical Thinking and the Higher-Order Cognitive Skills?It is not uncommon to associate creativity and ingenuity with scientific reasoning ( Sawyer, 2005 ; 2006 ). When instructors apply scientific teaching strategies ( Handelsman et al. , 2004 ; DeHaan, 2005 ; Wood, 2009 ) by using instructional methods based on learning research, according to Ebert-May and Hodder ( 2008 ), “we see students actively engaged in the thinking, creativity, rigor, and experimentation we associate with the practice of science—in much the same way we see students learn in the field and in laboratories” (p. 2). Perkins and Wieman (2008) note that “To be successful innovators in science and engineering, students must develop a deep conceptual understanding of the underlying science ideas, an ability to apply these ideas and concepts broadly in different contexts, and a vision to see their relevance and usefulness in real-world applications … An innovator is able to perceive and realize potential connections and opportunities better than others” (pp. 181–182). The results of Scott et al. (2004) suggest that nontraditional courses in science that are based on constructivist principles and that use strategies of scientific teaching to promote the HOCS and enhance content mastery and dexterity in scientific thinking ( Handelsman et al. , 2007 ; Nelson, 2008 ) also should be effective in promoting creativity and cognitive flexibility if students are explicitly guided to learn these skills. Creativity is an essential element of problem solving ( Mumford et al. , 1991 ; Runco, 2004 ) and of critical thinking ( Abrami et al. , 2008 ). As such, it is common to think of applications of creativity such as inventiveness and ingenuity among the HOCS as defined in Bloom's taxonomy ( Crowe et al. , 2008 ). Thus, it should come as no surprise that creativity, like other elements of the HOCS, can be taught most effectively through inquiry-based instruction, informed by constructivist theory ( Ausubel, 1963 , 2000 ; Duch et al. , 2001 ; Nelson, 2008 ). In a survey of 103 instructors who taught college courses that included creativity instruction, Bull et al. (1995) asked respondents to rate the importance of various course characteristics for enhancing student creativity. Items ranking high on the list were: providing a social climate in which students feels safe, an open classroom environment that promotes tolerance for ambiguity and independence, the use of humor, metaphorical thinking, and problem defining. Many of the responses emphasized the same strategies as those advanced to promote creative problem solving (e.g., Mumford et al. , 1991 ; McFadzean, 2002 ; Treffinger and Isaksen, 2005 ) and critical thinking ( Abrami et al. , 2008 ). In a careful meta-analysis, Scott et al. (2004) examined 70 instructional interventions designed to enhance and measure creative performance. The results were striking. Courses that stressed techniques such as critical thinking, convergent thinking, and constraint identification produced the largest positive effect sizes. More open techniques that provided less guidance in strategic approaches had less impact on the instructional outcomes. A striking finding was the effectiveness of being explicit; approaches that clearly informed students about the nature of creativity and offered clear strategies for creative thinking were most effective. Approaches such as social modeling, cooperative learning, and case-based (project-based) techniques that required the application of newly acquired knowledge were found to be positively correlated to high effect sizes. The most clear-cut result to emerge from the Scott et al. (2004) study was simply to confirm that creativity instruction can be highly successful in enhancing divergent thinking, problem solving, and imaginative performance. Most importantly, of the various cognitive processes examined, those linked to the generation of new ideas such as problem finding, conceptual combination, and idea generation showed the greatest improvement. The success of creativity instruction, the authors concluded, can be attributed to “developing and providing guidance concerning the application of requisite cognitive capacities … [and] a set of heuristics or strategies for working with already available knowledge” (p. 382). Many of the scientific teaching practices that have been shown by research to foster content mastery and HOCS, and that are coming more widely into use, also would be consistent with promoting creativity. Wood (2009) has recently reviewed examples of such practices and how to apply them. These include relatively small modifications of the traditional lecture to engender more active learning, such as the use of concept tests and peer instruction ( Mazur, 1996 ), Just-in-Time-Teaching techniques ( Novak et al. , 1999 ), and student response systems known as “clickers” ( Knight and Wood, 2005 ; Crossgrove and Curran, 2008 ), all designed to allow the instructor to frequently and effortlessly elicit and respond to student thinking. Other strategies can transform the lecture hall into a workshop or studio classroom ( Gaffney et al. , 2008 ) where the teaching curriculum may emphasize problem-based (also known as project-based or case-based) learning strategies ( Duch et al. , 2001 ; Ebert-May and Hodder, 2008 ) or “community-based inquiry” in which students engage in research that enhances their critical-thinking skills ( Quitadamo et al. , 2008 ). Another important approach that could readily subserve explicit creativity instruction is the use of computer-based interactive simulations, or “sims” ( Perkins and Wieman, 2008 ) to facilitate inquiry learning and effective, easy self-assessment. An example in the biological sciences would be Neurons in Action ( http://neuronsinaction.com/home/main ). In such educational environments, students gain conceptual understanding of scientific ideas through interactive engagement with materials (real or virtual), with each other, and with instructors. Following the tenets of scientific teaching, students are encouraged to pose and answer their own questions, to make sense of the materials, and to construct their own understanding. The question I pose here is whether an additional focus—guiding students to meet these challenges in a context that explicitly promotes creativity—would enhance learning and advance students' progress toward adaptive expertise? Assessment of CreativityTo teach creativity, there must be measurable indicators to judge how much students have gained from instruction. Educational programs intended to teach creativity became popular after the Torrance Tests of Creative Thinking (TTCT) was introduced in the 1960s ( Torrance, 1974 ). But it soon became apparent that there were major problems in devising tests for creativity, both because of the difficulty of defining the construct and because of the number and complexity of elements that underlie it. Tests of intelligence and other personality characteristics on creative individuals revealed a host of related traits such as verbal fluency, metaphorical thinking, flexible decision making, tolerance of ambiguity, willingness to take risks, autonomy, divergent thinking, self-confidence, problem finding, ideational fluency, and belief in oneself as being “creative” ( Barron and Harrington, 1981 ; Tardif and Sternberg, 1988 ; Runco and Nemiro, 1994 ; Snyder et al. , 2004 ). Many of these traits have been the focus of extensive research of recent decades, but, as noted above, creativity is not defined by any one trait; there is now reason to believe that it is the interplay among the cognitive and affective processes that underlie inventiveness and the ability to find novel solutions to a problem. Although the early creativity researchers recognized that assessing divergent thinking as a measure of creativity required tests for other underlying capacities ( Guilford, 1950 ; Torrance, 1974 ), these workers and their colleagues nonetheless believed that a high score for divergent thinking alone would correlate with real creative output. Unfortunately, no such correlation was shown ( Barron and Harrington, 1981 ). Results produced by many of the instruments initially designed to measure various aspects of creative thinking proved to be highly dependent on the test itself. A review of several hundred early studies showed that an individual's creativity score could be affected by simple test variables, for example, how the verbal pretest instructions were worded ( Barron and Harrington, 1981 , pp. 442–443). Most scholars now agree that divergent thinking, as originally defined, was not an adequate measure of creativity. The process of creative thinking requires a complex combination of elements that include cognitive flexibility, memory control, inhibitory control, and analogical thinking, enabling the mind to free-range and analogize, as well as to focus and test. More recently, numerous psychometric measures have been developed and empirically tested (see Plucker and Renzulli, 1999 ) that allow more reliable and valid assessment of specific aspects of creativity. For example, the creativity quotient devised by Snyder et al. (2004) tests the ability of individuals to link different ideas and different categories of ideas into a novel synthesis. The Wallach–Kogan creativity test ( Wallach and Kogan, 1965 ) explores the uniqueness of ideas associated with a stimulus. For a more complete list and discussion, see the Creativity Tests website ( www.indiana.edu/∼bobweb/Handout/cretv_6.html ). The most widely used measure of creativity is the TTCT, which has been modified four times since its original version in 1966 to take into account subsequent research. The TTCT-Verbal and the TTCT-Figural are two versions ( Torrance, 1998 ; see http://ststesting.com/2005giftttct.html ). The TTCT-Verbal consists of five tasks; the “stimulus” for each task is a picture to which the test-taker responds briefly in writing. A sample task that can be viewed from the TTCT Demonstrator website asks, “Suppose that people could transport themselves from place to place with just a wink of the eye or a twitch of the nose. What might be some things that would happen as a result? You have 3 min.” ( www.indiana.edu/∼bobweb/Handout/d3.ttct.htm ). In the TTCT-Figural, participants are asked to construct a picture from a stimulus in the form of a partial line drawing given on the test sheet (see example below; Figure 1 ). Specific instructions are to “Add lines to the incomplete figures below to make pictures out of them. Try to tell complete stories with your pictures. Give your pictures titles. You have 3 min.” In the introductory materials, test-takers are urged to “… think of a picture or object that no one else will think of. Try to make it tell as complete and as interesting a story as you can …” ( Torrance et al. , 2008 , p. 2).  Figure 1. Sample figural test item from the TTCT Demonstrator website ( www.indiana.edu/∼bobweb/Handout/d3.ttct.htm ). How would an instructor in a biology course judge the creativity of students' responses to such an item? To assist in this task, the TTCT has scoring and norming guides ( Torrance, 1998 ; Torrance et al. , 2008 ) with numerous samples and responses representing different levels of creativity. The guides show sample evaluations based upon specific indicators such as fluency, originality, elaboration (or complexity), unusual visualization, extending or breaking boundaries, humor, and imagery. These examples are easy to use and provide a high degree of validity and generalizability to the tests. The TTCT has been more intensively researched and analyzed than any other creativity instrument, and the norming samples have longitudinal validations and high predictive validity over a wide age range. In addition to global creativity scores, the TTCT is designed to provide outcome measures in various domains and thematic areas to allow for more insightful analysis ( Kaufman and Baer, 2006 ). Kim (2006) has examined the characteristics of the TTCT, including norms, reliability, and validity, and concludes that the test is an accurate measure of creativity. When properly used, it has been shown to be fair in terms of gender, race, community status, and language background. According to Kim (2006) and other authorities in the field ( McIntyre et al. , 2003 ; Scott et al. , 2004 ), Torrance's research and the development of the TTCT have provided groundwork for the idea that creative levels can be measured and then increased through instruction and practice. SCIENTIFIC TEACHING TO PROMOTE CREATIVITYHow could creativity instruction be integrated into scientific teaching. Guidelines for designing specific course units that emphasize HOCS by using strategies of scientific teaching are now available from the current literature. As an example, Karen Cloud-Hansen and colleagues ( Cloud-Hansen et al. , 2008 ) describe a course titled, “Ciprofloxacin Resistance in Neisseria gonorrhoeae .” They developed this undergraduate seminar to introduce college freshmen to important concepts in biology within a real-world context and to increase their content knowledge and critical-thinking skills. The centerpiece of the unit is a case study in which teams of students are challenged to take the role of a director of a local public health clinic. One of the county commissioners overseeing the clinic is an epidemiologist who wants to know “how you plan to address the emergence of ciprofloxacin resistance in Neisseria gonorrhoeae ” (p. 304). State budget cuts limit availability of expensive antibiotics and some laboratory tests to patients. Student teams are challenged to 1) develop a plan to address the medical, economic, and political questions such a clinic director would face in dealing with ciprofloxacin-resistant N. gonorrhoeae ; 2) provide scientific data to support their conclusions; and 3) describe their clinic plan in a one- to two-page referenced written report. Throughout the 3-wk unit, in accordance with the principles of problem-based instruction ( Duch et al. , 2001 ), course instructors encourage students to seek, interpret, and synthesize their own information to the extent possible. Students have access to a variety of instructional formats, and active-learning experiences are incorporated throughout the unit. These activities are interspersed among minilectures and give the students opportunities to apply new information to their existing base of knowledge. The active-learning activities emphasize the key concepts of the minilectures and directly confront common misconceptions about antibiotic resistance, gene expression, and evolution. Weekly classes include question/answer/discussion sessions to address student misconceptions and 20-min minilectures on such topics as antibiotic resistance, evolution, and the central dogma of molecular biology. Students gather information about antibiotic resistance in N. gonorrhoeae , epidemiology of gonorrhea, and treatment options for the disease, and each team is expected to formulate a plan to address ciprofloxacin resistance in N. gonorrhoeae . In this project, the authors assessed student gains in terms of content knowledge regarding topics covered such as the role of evolution in antibiotic resistance, mechanisms of gene expression, and the role of oncogenes in human disease. They also measured HOCS as gains in problem solving, according to a rubric that assessed self-reported abilities to communicate ideas logically, solve difficult problems about microbiology, propose hypotheses, analyze data, and draw conclusions. Comparing the pre- and posttests, students reported significant learning of scientific content. Among the thinking skill categories, students demonstrated measurable gains in their ability to solve problems about microbiology but the unit seemed to have little impact on their more general perceived problem-solving skills ( Cloud-Hansen et al. , 2008 ). What would such a class look like with the addition of explicit creativity-promoting approaches? Would the gains in problem-solving abilities have been greater if during the minilectures and other activities, students had been introduced explicitly to elements of creative thinking from the Sternberg and Williams (1998) list described above? Would the students have reported greater gains if their instructors had encouraged idea generation with weekly brainstorming sessions; if they had reminded students to cross-fertilize ideas by integrating material across subject areas; built self-efficacy by helping students believe in their own capacity to be creative; helped students question their own assumptions; and encouraged students to imagine other viewpoints and possibilities? Of most relevance, could the authors have been more explicit in assessing the originality of the student plans? In an experiment that required college students to develop plans of a different, but comparable, type, Osborn and Mumford (2006) created an originality rubric ( Figure 2 ) that could apply equally to assist instructors in judging student plans in any course. With such modifications, would student gains in problem-solving abilities or other HOCS have been greater? Would their plans have been measurably more imaginative?  Figure 2. Originality rubric (adapted from Osburn and Mumford, 2006 , p. 183). Answers to these questions can only be obtained when a course like that described by Cloud-Hansen et al. (2008) is taught with explicit instruction in creativity of the type I described above. But, such answers could be based upon more than subjective impressions of the course instructors. For example, students could be pretested with items from the TTCT-Verbal or TTCT-Figural like those shown. If, during minilectures and at every contact with instructors, students were repeatedly reminded and shown how to be as creative as possible, to integrate material across subject areas, to question their own assumptions and imagine other viewpoints and possibilities, would their scores on TTCT posttest items improve? Would the plans they formulated to address ciprofloxacin resistance become more imaginative? Recall that in their meta-analysis, Scott et al. (2004) found that explicitly informing students about the nature of creativity and offering strategies for creative thinking were the most effective components of instruction. From their careful examination of 70 experimental studies, they concluded that approaches such as social modeling, cooperative learning, and case-based (project-based) techniques that required the application of newly acquired knowledge were positively correlated with high effect sizes. The study was clear in confirming that explicit creativity instruction can be successful in enhancing divergent thinking and problem solving. Would the same strategies work for courses in ecology and environmental biology, as detailed by Ebert-May and Hodder (2008) , or for a unit elaborated by Knight and Wood (2005) that applies classroom response clickers? Finally, I return to my opening question with the fictional Dr. Dunne. Could a weekly brainstorming “invention session” included in a course like those described here serve as the site where students are introduced to concepts and strategies of creative problem solving? As frequently applied in schools of engineering ( Paulus and Nijstad, 2003 ), brainstorming provides an opportunity for the instructor to pose a problem and to ask the students to suggest as many solutions as possible in a brief period, thus enhancing ideational fluency. Here, students can be encouraged explicitly to build on the ideas of others and to think flexibly. Would brainstorming enhance students' divergent thinking or creative abilities as measured by TTCT items or an originality rubric? Many studies have demonstrated that group interactions such as brainstorming, under the right conditions, can indeed enhance creativity ( Paulus and Nijstad, 2003 ; Scott et al. , 2004 ), but there is little information from an undergraduate science classroom setting. Intellectual Ventures, a firm founded by Nathan Myhrvold, the creator of Microsoft's Research Division, has gathered groups of engineers and scientists around a table for day-long sessions to brainstorm about a prearranged topic. Here, the method seems to work. Since it was founded in 2000, Intellectual Ventures has filed hundreds of patent applications in more than 30 technology areas, applying the “invention session” strategy ( Gladwell, 2008 ). Currently, the company ranks among the top 50 worldwide in number of patent applications filed annually. Whether such a technique could be applied successfully in a college science course will only be revealed by future research. - Abrami P. C., Bernard R. M., Borokhovski E., Wadem A., Surkes M. A., Tamim R., Zhang D. ( 2008 ). Instructional interventions affecting critical thinking skills and dispositions: a stage 1 meta-analysis . Rev. Educ. Res 78 , 1102-1134. Google Scholar
- Amabile T. M. ( 1996 ). Creativity in Context , Boulder, CO: Westview Press. Google Scholar
- Amabile T. M., Barsade S. G., Mueller J. S., Staw B. M. ( 2005 ). Affect and creativity at work . Admin. Sci. Q 50 , 367-403. Google Scholar
- Ausubel D. ( 1963 ). The Psychology of Meaningful Verbal Learning , New York: Grune and Stratton. Google Scholar
- Ausubel B. ( 2000 ). The Acquisition and Retention of Knowledge: A Cognitive View , Boston, MA: Kluwer Academic Publishers. Google Scholar
- Banaji S., Burn A., Buckingham D. ( 2006 ). The Rhetorics of Creativity: A Review of the Literature , accessed 29 December 2008 London: Centre for the Study of Children, Youth and Media, www.creativepartnerships.com/data/files/rhetorics-of-creativity-12.pdf . Google Scholar
- Barron F., Harrington D. M. ( 1981 ). Creativity, intelligence and personality . Ann. Rev. Psychol 32 , 439-476. Google Scholar
- Beller M. ( 1999 ). Quantum Dialogue: The Making of a Revolution , Chicago, IL: University of Chicago Press. Google Scholar
- Blair C., Razza R. P. ( 2007 ). Relating effortful control, executive function, and false belief understanding to emerging math and literacy ability in kindergarten . Child Dev 78 , 647-663. Medline , Google Scholar
- Bodrova E., Leong D. J. ( 2001 ). The Tool of the Mind: a case study of implementing the Vygotskian approach In: American Early Childhood and Primary Classrooms , Geneva, Switzerland: UNESCO International Bureau of Education. Google Scholar
- Bransford J. D.Brown A. L.Cocking R. R. ( 2000 ). How People Learn: Brain, Mind, Experience, and School , Washington, DC: National Academies Press. Google Scholar
- Brophy D. R. ( 2006 ). A comparison of individual and group efforts to creatively solve contrasting types of problems . Creativity Res. J 18 , 293-315. Google Scholar
- Bruner J. ( 1965 ). The growth of mind . Am. Psychol 20 , 1007-1017. Medline , Google Scholar
- Bull K. S., Montgomery D., Baloche L. ( 1995 ). Teaching creativity at the college level: a synthesis of curricular components perceived as important by instructors . Creativity Res. J 8 , 83-90. Google Scholar
- Burton R. ( 2008 ). On Being Certain: Believing You Are Right Even When You're Not , New York: St. Martin's Press. Google Scholar
- Cloud-Hanson K. A., Kuehner J. N., Tong L., Miller S., Handelsman J. ( 2008 ). Money, sex and drugs: a case study to teach the genetics of antibiotic resistance . CBE Life Sci. Educ 7 , 302-309. Medline , Google Scholar
- Craft A. ( 2000 ). Teaching Creativity: Philosophy and Practice , New York: Routledge. Google Scholar
- Crawford V. M. ( 2007 ). Adaptive expertise as knowledge building in science teachers' problem solving accessed 1 July 2008 Proceedings of the Second European Cognitive Science Conference Delphi, Greece http://ctl.sri.com/publications/downloads/Crawford_EuroCogSci07Proceedings.pdf . Google Scholar
- Crawford V. M., Brophy S. ( 2006 ). Adaptive Expertise: Theory, Methods, Findings, and Emerging Issues; September 2006 In: accessed 1 July 2008 Menlo Park, CA: SRI International, http://ctl.sri.com/publications/downloads/AESymposiumReportOct06.pdf . Google Scholar
- Crossgrove K., Curran K. L. ( 2008 ). Using clickers in nonmajors- and majors-level biology courses: student opinion, learning, and long-term retention of course material . CBE Life Sci. Educ 7 , 146-154. Link , Google Scholar
- Crowe A., Dirks C., Wenderoth M. P. ( 2008 ). Biology in bloom: implementing Bloom's taxonomy to enhance student learning in biology . CBE Life Sci. Educ 7 , 368-381. Link , Google Scholar
- Davidson M. C., Amso D., Anderson L. C., Diamond A. ( 2006 ). Development of cognitive control and executive functions from 4–13 years: evidence from manipulations of memory, inhibition, and task switching . Neuropsychologia 44 , 2037-2078. Medline , Google Scholar
- DeHaan R. L. ( 2005 ). The impending revolution in undergraduate science education . J. Sci. Educ. Technol 14 , 253-270. Google Scholar
- Diamond A., Barnett W. S., Thomas J., Munro S. ( 2007 ). Preschool program improves cognitive control . Science 318 , 1387-1388. Medline , Google Scholar
- Duch B. J., Groh S. E., Allen D. E. ( 2001 ). The Power of Problem-based Learning , Sterling, VA: Stylus Publishers. Google Scholar
- Durston S., Davidson M. C., Thomas K. M., Worden M. S., Tottenham N., Martinez A., Watts R., Ulug A. M., Caseya B. J. ( 2003 ). Parametric manipulation of conflict and response competition using rapid mixed-trial event-related fMRI . Neuroimage 20 , 2135-2141. Medline , Google Scholar
- Ebert-May D., Hodder J. ( 2008 ). Pathways to Scientific Teaching , Sunderland, MA: Sinauer. Google Scholar
- Finke R. A., Ward T. B., Smith S. M. ( 1996 ). Creative Cognition: Theory, Research and Applications , Boston, MA: MIT Press. Google Scholar
- Freeman S., O'Connor E., Parks J. W., Cunningham M., Hurley D., Haak D., Dirks C., Wenderoth M. P. ( 2007 ). Prescribed active learning increases performance in introductory biology . CBE Life Sci. Educ 6 , 132-139. Link , Google Scholar
- Gabora L. ( 2002 ). Hewett T.Kavanagh E. Cognitive mechanisms underlying the creative process Proceedings of the Fourth International Conference on Creativity and Cognition 2002 October 13–16 Loughborough University, United Kingdom 126-133. Google Scholar
- Gaffney J.D.H., Richards E., Kustusch M. B., Ding L., Beichner R. ( 2008 ). Scaling up education reform . J. Coll. Sci. Teach 37 , 48-53. Google Scholar
- Gardner H. ( 1993 ). Creating Minds: An Anatomy of Creativity Seen through the Lives of Freud, Einstein, Picasso, Stravinsky, Eliot, Graham, and Ghandi In: New York: Harper Collins. Google Scholar
- Gladwell M. ( 2008 ). In the air; who says big ideas are rare? The New Yorker accessed 19 May 2008 www.newyorker.com/reporting/2008/05/12/080512fa_fact_gladwell . Google Scholar
- Guilford J. P. ( 1950 ). Creativity . Am. Psychol 5 , 444-454. Medline , Google Scholar
- Hake R. ( 2005 ). The physics education reform effort: a possible model for higher education . Natl. Teach. Learn. Forum 15 , 1-6. Google Scholar
- Halpern D. E., Hakel M. D. ( 2003 ). Applying the science of learning to the university and beyond . Change 35 , 36-42. Google Scholar
- Handelsman J. ( 2004 ). Scientific teaching . Science 304 , 521-522. Medline , Google Scholar
- Handelsman J, Miller S., Pfund C. ( 2007 ). Scientific Teaching , New York: W. H. Freeman and Co. Google Scholar
- Haring-Smith T. ( 2006 ). Creativity research review: some lessons for higher education. Association of American Colleges and Universities . Peer Rev 8 , 23-27. Google Scholar
- Hatano G., Ouro Y. ( 2003 ). Commentary: reconceptualizing school learning using insight from expertise research . Educ. Res 32 , 26-29. Google Scholar
- Hrepic Z., Zollman D. A., Rebello N. S. ( 2007 ). Comparing students' and experts' understanding of the content of a lecture . J. Sci. Educ. Technol 16 , 213-224. Google Scholar
- Hunsaker S. L. ( 2005 ). Outcomes of creativity training programs . Gifted Child Q 49 , 292-298. Google Scholar
- Kaufman J. C., Baer J. ( 2006 ). Intelligent testing with Torrance . Creativity Res. J 18 , 99-102. Google Scholar
- Kaufman J. C., Beghetto R. A. ( 2008 , Ed. R. L. DeHaanK.M.V. Narayan , Exploring mini-C: creativity across cultures In: Education for Innovation: Implications for India, China and America , Rotterdam, The Netherlands: Sense Publishers, 165-180. Google Scholar
- Kaufman J. C., Sternberg R. J. ( 2007 ). Creativity . Change 39 , 55-58. Google Scholar
- Kim K. H. ( 2006 ). Can we trust creativity tests: a review of the Torrance Tests of Creative Thinking (TTCT) . Creativity Res. J 18 , 3-14. Google Scholar
- Knight J. K., Wood W. B. ( 2005 ). Teaching more by lecturing less . Cell Biol. Educ 4 , 298-310. Link , Google Scholar
- Cetina Knorr K. ( 1995 , Ed. S. JasanoffG. MarkleJ. PetersenT. Pinch , Laboratory studies: the cultural approach to the study of science In: Handbook of Science and Technology Studies , Thousand Oaks, CA: Sage Publications, 140-166. Google Scholar
- Koestler A. ( 1964 ). The Act of Creation , New York: Macmillan. Google Scholar
- Latour B., Woolgar S. ( 1986 ). Laboratory Life: The Construction of Scientific Facts , Princeton, NJ: Princeton University Press. Google Scholar
- MacKinnon D. W. ( 1978 , Ed. D. W. MacKinnon , What makes a person creative? In: In Search of Human Effectiveness , New York: Universe Books, 178-186. Google Scholar
- Martindale C. ( 1999 , Ed. R. J. Sternberg , Biological basis of creativity In: Handbook of Creativity , Cambridge, United Kingdom: Cambridge University Press, 137-152. Google Scholar
- Mazur E. ( 1996 ). Peer Instruction: A User's Manual , Upper Saddle River, NJ: Prentice Hall. Google Scholar
- McFadzean E. ( 2002 ). Developing and supporting creative problem-solving teams: Part 1—a conceptual model . Manage. Decis 40 , 463-475. Google Scholar
- McGregor G. D. ( 2001 ). Creative thinking instruction for a college study skills program: a case study. . Dissert Abstr. Intl 62 , 3293A UMI No. AAT 3027933. Google Scholar
- McIntyre F. S., Hite R. E., Rickard M. K. ( 2003 ). Individual characteristics and creativity in the marketing classroom: exploratory insights . J. Mark. Educ 25 , 143-149. Google Scholar
- Mestre J. P. ( 2005 ). Transfer of Learning: From a Modern Multidisciplinary Perspective , Greenwich, CT: Information Age Publishing. Google Scholar
- Mumford M. D., Mobley M. I., Uhlman C. E., Reiter-Palmon R., Doares L. M. ( 1991 ). Process analytic models of creative capacities . Creativity Res. J 4 , 91-122. Google Scholar
- National Research Council ( 2007 ). Rising Above the Gathering Storm: Energizing and Employing America for a Brighter Economic Future, Committee on Science, Engineering and Public Policy In: Washington, DC: National Academies Press. Google Scholar
- Neisser U. ( 1963 ). The multiplicity of thought . Br. J. Psychol 54 , 1-14. Medline , Google Scholar
- Nelson C. E. ( 2008 ). Teaching evolution (and all of biology) more effectively: strategies for engagement, critical reasoning, and confronting misconceptions Integrative and Comparative Biology Advance Access accessed 15 September 2008 http://icb.oxfordjournals.org/cgi/reprint/icn027v1.pdf . Google Scholar
- Novak G, Gavrin A., Christian W, Patterson E. ( 1999 ). Just-in-Time Teaching: Blending Active Learning with Web Technology , San Francisco, CA: Pearson Benjamin Cummings. Google Scholar
- Osborn A. F. ( 1948 ). Your Creative Power , New York: Scribner. Google Scholar
- Osborn A. F. ( 1979 ). Applied Imagination , New York: Scribner. Google Scholar
- Osburn H. K., Mumford M. D. ( 2006 ). Creativity and planning: training interventions to develop creative problem-solving skills . Creativity Res. J 18 , 173-190. Google Scholar
- Paulus P. B., Nijstad B. A. ( 2003 ). Group Creativity: Innovation through Collaboration , New York: Oxford University Press. Google Scholar
- Perkins K. K., Wieman C. E. ( 2008 , Ed. R. L. DeHaanK.M.V. Narayan , Innovative teaching to promote innovative thinking In: Education for Innovation: Implications for India, China and America , Rotterdam, The Netherlands: Sense Publishers, 181-210. Google Scholar
- Plucker J. A., Renzulli J. S. ( 1999 , Ed. R. J. Sternberg , Psychometric approaches to the study of human creativity In: Handbook of Creativity , Cambridge, United Kingdom: Cambridge University Press, 35-61. Google Scholar
- Quitadamo I. J., Faiola C. L., Johnson J. E., Kurtz M. J. ( 2008 ). Community-based inquiry improves critical thinking in general education biology . CBE Life Sci. Educ 7 , 327-337. Link , Google Scholar
- Runco M. A. ( 2004 ). Creativity . Annu. Rev. Psychol 55 , 657-687. Medline , Google Scholar
- Runco M. A., Nemiro J. ( 1994 ). Problem finding, creativity, and giftedness . Roeper Rev 16 , 235-241. Google Scholar
- Sawyer R. K. ( 2005 ). Educating for Innovation Thinking Skills Creativity accessed 13 August 2008 1 41-48 www.artsci.wustl.edu/∼ksawyer/PDFs/Thinkjournal.pdf . Google Scholar
- Sawyer R. K. ( 2006 ). Explaining Creativity: The Science of Human Innovation , New York: Oxford University Press. Google Scholar
- Schwartz D. L., Bransford J. D., Sears D. ( 2005 , Ed. J. P. Mestre , Efficiency and innovation in transfer In: Transfer of Learning from a Modern Multidisciplinary Perspective , Greenwich, CT: Information Age Publishing, 1-51. Google Scholar
- Scott G., Leritz L. E., Mumford M. D. ( 2004 ). The effectiveness of creativity training: a quantitative review . Creativity Res. J 16 , 361-388. Google Scholar
- Simonton D. K. ( 1975 ). Sociocultural context of individual creativity: a transhistorical time-series analysis . J. Pers. Soc. Psychol 32 , 1119-1133. Medline , Google Scholar
- Simonton D. K. ( 2004 ). Creativity in Science: Chance, Logic, Genius, and Zeitgeist , Oxford, United Kingdom: Cambridge University Press. Google Scholar
- Sloman S. ( 1996 ). The empirical case for two systems of reasoning . Psychol. Bull 9 , 3-22. Google Scholar
- Smith G. F. ( 1998 ). Idea generation techniques: a formulary of active ingredients . J. Creative Behav 32 , 107-134. Google Scholar
- Snyder A., Mitchell J., Bossomaier T., Pallier G. ( 2004 ). The creativity quotient: an objective scoring of ideational fluency . Creativity Res. J 16 , 415-420. Google Scholar
- Sternberg R. J. ( 2003 ). What is an “expert student?” . Educ. Res. 32 , 5-9. Google Scholar
- Sternberg R., Williams W. M. ( 1998 ). Teaching for creativity: two dozen tips accessed 25 March 2008 www.cdl.org/resource-library/articles/teaching_creativity.php . Google Scholar
- Tardif T. Z., Sternberg R. J. ( 1988 , Ed. R. J. Sternberg , What do we know about creativity? In: The Nature of Creativity , New York: Cambridge University Press, 429-440. Google Scholar
- Torrance E. P. ( 1974 ). Norms and Technical Manual for the Torrance Tests of Creative Thinking , Bensenville, IL: Scholastic Testing Service. Google Scholar
- Torrance E. P. ( 1998 ). The Torrance Tests of Creative Thinking Norms—Technical Manual Figural (Streamlined) Forms A and B , Bensenville, IL: Scholastic Testing Service. Google Scholar
- Torrance E. P., Ball O. E., Safter H. T. ( 2008 ). Torrance Tests of Creative Thinking: Streamlined Scoring Guide for Figural Forms A and B , Bensenville, IL: Scholastic Testing Service. Google Scholar
- Treffinger D. J., Isaksen S. G. ( 2005 ). Creative problem solving: the history, development, and implications for gifted education and talent development . Gifted Child Q 49 , 342-357. Google Scholar
- Vandervert L. R., Schimpf P. H., Liu H. ( 2007 ). How working memory and the cerebellum collaborate to produce creativity and innovation . Creativity Res. J 9 , 1-18. Google Scholar
- Wallach M. A., Kogan N. ( 1965 ). Modes of Thinking in Young Children: A Study of the Creativity-Intelligence Distinction , New York: Holt, Rinehart and Winston. Google Scholar
- Wood W. B. ( 2009 ). Innovations in undergraduate biology teaching and why we need them . Annu. Rev. Cell Dev. Biol in press. Medline , Google Scholar
- ChatGPT improves creative problem-solving performance in university students: An experimental study 1 Jul 2024 | Computers & Education, Vol. 215
- Are we teaching novice instructional designers to be creative? A qualitative case study 16 January 2024 | Instructional Science, Vol. 52, No. 3
- Educators as agents of breadth-biased learning: using social reconstructionism as rationale for embracing media multitasking and enhancing teaching practices in higher education 3 April 2024 | Frontiers in Psychology, Vol. 15
- Searching for creativity: How people search to generate new ideas 1 December 2023 | Journal of the Association for Information Science and Technology, Vol. 75, No. 4
- Fostering creativity in low-engagement students through socratic dialogue: An experiment in an operations class 1 Mar 2024 | The International Journal of Management Education, Vol. 22, No. 1
- Cognitive flexibility and academic performance: Individual and cross-national patterns among adolescents in 57 countries 1 Feb 2024 | Personality and Individual Differences, Vol. 217
- What's in a word? Student beliefs and understanding about green chemistry 1 January 2024 | Chemistry Education Research and Practice, Vol. 25, No. 1
- Preservice Physical Education Teachers’ Resistance to Change: The Importance of Occupational Socialization Experiences 26 October 2023 | Trends in Higher Education, Vol. 2, No. 4
- How can we measure metacognition in creative problem-solving? Standardization of the MCPS scale 1 Sep 2023 | Thinking Skills and Creativity, Vol. 49
- TOWARDS ENHANCING CREATIVITY AND INNOVATION IN EDUCATION SYSTEM FOR YOUTH IN HAIL REGION 1 August 2023 | Advanced Education, Vol. 10, No. 22
- Investigating the impact of innovation competence instruction in higher engineering education 12 June 2023 | European Journal of Engineering Education, Vol. 10
- Regaining creativity in science: insights from conversation 17 May 2023 | Royal Society Open Science, Vol. 10, No. 5
- How transdisciplinary integration, creativity and student motivation interact in three STEAM projects for gifted education? 29 March 2023 | Gifted Education International, Vol. 39, No. 2
- Does creative coursework predict educational, career, and community engagement outcomes for arts alumni? 15 November 2022 | Creativity Research Journal, Vol. 35, No. 2
- Make science disruptive again 27 March 2023 | Nature Biotechnology, Vol. 41, No. 4
- Promoting Creativity in Undergraduate Recreation and Leisure Services Classrooms: An Overview 19 March 2021 | SCHOLE: A Journal of Leisure Studies and Recreation Education, Vol. 38, No. 1
- A Positive Association between Working Memory Capacity and Human Creativity: A Meta-Analytic Evidence 13 January 2023 | Journal of Intelligence, Vol. 11, No. 1
- Students Creativity Through Digital Mind Map 26 July 2023
- Pedagogical and School Practices to Foster Key Competences and Domain-General Literacy 23 August 2023
- Coping with Challenges and Uncertainty in Scientific Research 13 Dec 2022 | Asia-Pacific Science Education, Vol. 8, No. 2
- Teaching design thinking as a tool to address complex public health challenges in public health students: a case study 12 April 2022 | BMC Medical Education, Vol. 22, No. 1
- ‘Allowing them to dream’: fostering creativity in mathematics undergraduates 26 May 2022 | Journal of Further and Higher Education, Vol. 46, No. 10
- Interaction with metaphors enhances creative potential 1 July 2022 | Journal of Poetry Therapy, Vol. 35, No. 4
- Creative problem solving in knowledge-rich contexts 1 Oct 2022 | Trends in Cognitive Sciences, Vol. 26, No. 10
- Teaching Protein–Ligand Interactions Using a Case Study on Tau in Alzheimer’s Disease 1 July 2022 | Journal of Chemical Education, Vol. 99, No. 8
- The Effectiveness of Collaborative Learning on Critical Thinking, Creative Thinking, and Metacognitive Skill Ability: Meta-Analysis on Biological Learning 15 July 2022 | European Journal of Educational Research, Vol. volume-11-2022, No. volume-11-issue-3-july-2022
- Student approaches to creative processes when participating in an open-ended project in science 30 June 2022 | International Journal of Science Education, Vol. 44, No. 10
- Arts, Machines, and Creative Education 24 Jun 2022
- Perceived Learning Effectiveness and Student Satisfaction 6 May 2022
- A Contribution to Scientific Creativity: A Validation Study Measuring Divergent Problem Solving Ability 3 September 2021 | Creativity Research Journal, Vol. 34, No. 2
- Problem Solving and Digital Transformation: Acquiring Skills through Pretend Play in Kindergarten 28 January 2022 | Education Sciences, Vol. 12, No. 2
- Growing Innovation and Collaboration Through Assessment and Feedback: A Toolkit for Assessing and Developing Students’ Soft Skills in Biological Experimentation 12 May 2022
- The Role of Creativity in Teaching Mathematics Online 1 December 2022
- Breathing Life Into Marketing Scholarship Through Creativity Learning and Teaching 1 Jan 2022
- Mobilizing Research-Based Learning (RBL) in Higher Education 1 Jan 2022
- Trends and opportunities by fostering creativity in science and engineering: a systematic review 2 September 2021 | European Journal of Engineering Education, Vol. 46, No. 6
- The effect of a scientific board game on improving creative problem solving skills 1 Sep 2021 | Thinking Skills and Creativity, Vol. 41
- Create Teaching Creativity through Training Management, Effectiveness Training, and Teacher Quality in the Covid-19 Pandemic 6 August 2021 | Journal of Ethnic and Cultural Studies, Vol. 8, No. 4
- Creativity and technology in teaching and learning: a literature review of the uneasy space of implementation 11 January 2021 | Educational Technology Research and Development, Vol. 69, No. 4
- Üstün Yetenekli Öğrencilerin Bilimsel Yaratıcılık ve Bilimsel Problem Çözme ile İlgili Öz Değerlendirmeleri 15 July 2021 | Yuzunci Yil Universitesi Egitim Fakultesi Dergisi
- Cultivating creative thinking in engineering student teams: Can a computer‐mediated virtual laboratory help? 23 November 2020 | Journal of Computer Assisted Learning, Vol. 37, No. 2
- Entrepreneurial competencies of undergraduate students: The case of universities in Nigeria 1 Mar 2021 | The International Journal of Management Education, Vol. 19, No. 1
- Promoting Creativity in General Education Mathematics Courses 5 August 2019 | PRIMUS, Vol. 31, No. 1
- Methodological Considerations for Understanding Students’ Problem Solving Processes and Affective Trajectories During Game-Based Learning: A Data Fusion Approach 3 July 2021
- The main trends in the process of building the creative potential of engineering students 18 June 2021 | E3S Web of Conferences, Vol. 274
- Research on the Present Situation and Countermeasures of Cultivating Graduate Students’ Innovation Ability under Cooperative Innovation Environment 1 Jan 2021 | Creative Education Studies, Vol. 09, No. 02
- Innovation Centers and the Information Schools: The Influence of LIS Faculty 1 Dec 2020 | Journal of Education for Library and Information Science, Vol. 61, No. 4
- Biomimetics: teaching the tools of the trade 28 September 2020 | FEBS Open Bio, Vol. 10, No. 11
- STEM academic teachers’ experiences of undertaking authentic assessment-led reform: a mixed method approach 21 March 2019 | Studies in Higher Education, Vol. 45, No. 9
- Problems of forming marketing competencies in the digital economy 1 Sep 2020 | IOP Conference Series: Materials Science and Engineering, Vol. 940, No. 1
- Culturally Responsive Assessment of Physical Science Skills and Abilities: Development, Field Testing, Implementation, and Results 2 June 2020 | Journal of Advanced Academics, Vol. 31, No. 3
- Culturally Responsive Assessment of Life Science Skills and Abilities: Development, Field Testing, Implementation, and Results 3 June 2020 | Journal of Advanced Academics, Vol. 31, No. 3
- Curriculum Differentiation’s Capacity to Extend Gifted Students in Secondary Mixed-ability Science Classes 27 June 2020 | Talent, Vol. 10, No. 1
- Student Motivation from and Resistance to Active Learning Rooted in Essential Science Practices 23 December 2017 | Research in Science Education, Vol. 50, No. 1
- Integrating Entrepreneurship and Art to Improve Creative Problem Solving in Fisheries Education 27 February 2020 | Fisheries, Vol. 45, No. 2
- Concepts Re-imagined: Relational Signs Beyond Definitional Rigidity 15 August 2020
- Promoting Student Creativity and Inventiveness in Science and Engineering 24 October 2020
- Teaching for Leadership, Innovation, and Creativity 1 Jan 2020
- Problem Çözme Becerileri Eğitim Programının Çocukların Karar Verme Becerileri Üzerindeki Etkisi 30 December 2019 | Erzincan Üniversitesi Eğitim Fakültesi Dergisi, Vol. 21, No. 3
- Mento’s change model in teaching competency-based medical education 27 December 2019 | BMC Medical Education, Vol. 19, No. 1
- The Effects of Individual Preparations on Group Creativity 21 January 2020
- The Value of Creativity for Enhancing Translational Ecologies, Insights, and Discoveries 9 July 2019 | Frontiers in Psychology, Vol. 10
- Using the International Classification of Functioning, Disability, and Health to Guide Students' Clinical Approach to Aging With Pathology 1 Jul 2019 | Topics in Geriatric Rehabilitation, Vol. 35, No. 3
- Impact of Brainstorming Strategy in Dealing With Knowledge Retention Skill: An Insight Into Special Learners' Needs In Saudi Arabia 1 January 2021 | MIER Journal of Educational Studies Trends & Practices
- The potential of students’ creative disposition as a perspective to develop creative teaching and learning for senior high school biological science 12 March 2019 | Journal of Physics: Conference Series, Vol. 1157
- Evaluating Remote Experiment from a Divergent Thinking Point of View 25 July 2018
- Exploring Creative Education Practices and Implications: A Case study of National Chengchi University, Taiwan 4 April 2022 | Journal of Business and Economic Analysis, Vol. 02, No. 02
- Exploring Creative Education Practices and Implications: A Case study of National Chengchi University, Taiwan 1 January 2020 | Journal of Business and Economic Analysis, Vol. 02, No. 02
- Diverging from the Dogma: A Call to Train Creative Thinkers in Science 14 September 2018 | The Bulletin of the Ecological Society of America, Vol. 100, No. 1
- Comparison of German and Japanese student teachers’ views on creativity in chemistry class 16 May 2018 | Asia-Pacific Science Education, Vol. 4, No. 1
- The use of humour during a collaborative inquiry 27 August 2018 | International Journal of Science Education, Vol. 40, No. 14
- Connecting creative coursework exposure and college student engagement across academic disciplines 29 August 2019 | Gifted and Talented International, Vol. 33, No. 1-2
- Views of German chemistry teachers on creativity in chemistry classes and in general 1 January 2018 | Chemistry Education Research and Practice, Vol. 19, No. 3
- Embedding Critical and Creative Thinking in Chemical Engineering Practice 1 Jul 2018
- Introducing storytelling to educational robotic activities 1 Apr 2018
- Investigating Undergraduates’ Perceptions of Science in Courses Taught Using the CREATE Strategy 1 Mar 2018 | Journal of Microbiology & Biology Education, Vol. 19, No. 1
- Teachers’ learning on the workshop of STS approach as a way of enhancing inventive thinking skills 1 Jan 2018
- Creativity Development Through Inquiry-Based Learning in Biomedical Sciences 1 Jan 2018
- The right tool for the right task: Structured techniques prove less effective on an ill-defined problem finding task 1 Dec 2017 | Thinking Skills and Creativity, Vol. 26
- The influential factors and hierarchical structure of college students’ creative capabilities—An empirical study in Taiwan 1 Dec 2017 | Thinking Skills and Creativity, Vol. 26
- Teacher perceptions of professional role and innovative teaching at elementary schools in Taiwan 10 November 2017 | Educational Research and Reviews, Vol. 12, No. 21
- Evaluation of creative problem-solving abilities in undergraduate structural engineers through interdisciplinary problem-based learning 28 July 2016 | European Journal of Engineering Education, Vol. 42, No. 6
- What Shall I Write Next? 19 September 2017
- Inquiry-based Laboratory Activities on Drugs Analysis for High School Chemistry Learning 3 October 2017 | Journal of Physics: Conference Series, Vol. 895
- BARRIERS TO STUDENTS’ CREATIVE EVALUATION OF UNEXPECTED EXPERIMENTAL FINDINGS 25 June 2017 | Journal of Baltic Science Education, Vol. 16, No. 3
- Kyle J. Frantz ,
- Melissa K. Demetrikopoulos ,
- Shari L. Britner ,
- Laura L. Carruth ,
- Brian A. Williams ,
- John L. Pecore ,
- Robert L. DeHaan , and
- Christopher T. Goode
- Elizabeth Ambos, Monitoring Editor
- A present absence: undergraduate course outlines and the development of student creativity across disciplines 3 October 2016 | Teaching in Higher Education, Vol. 22, No. 2
- Exploring differences in creativity across academic majors for high-ability college students 16 February 2018 | Gifted and Talented International, Vol. 32, No. 1
- Creativity in chemistry class and in general – German student teachers’ views 1 January 2017 | Chemistry Education Research and Practice, Vol. 18, No. 2
- IMPORTANCE OF CREATIVITY IN ENTREPRENEURSHIP 1 January 2017
- Accessing the Finest Minds 1 Jan 2017
- Science and Innovative Thinking for Technical and Organizational Development 1 Jan 2017
- Learning High School Biology in a Social Context 1 Jan 2017 | Creative Education, Vol. 08, No. 15
- Possibilities and limitations of integrating peer instruction into technical creativity education 6 September 2016 | Instructional Science, Vol. 44, No. 6
- Creative Cognitive Processes in Higher Education 20 November 2014 | The Journal of Creative Behavior, Vol. 50, No. 4
- An Evidence-Based Review of Creative Problem Solving Tools 6 April 2016 | Human Resource Development Review, Vol. 15, No. 2
- Case-based exams for learning and assessment: Experiences in an information systems course 1 Apr 2016
- Case exams for assessing higher order learning: A comparative social media analytics usage exam 1 Apr 2016
- Beyond belief: Structured techniques prove more effective than a placebo intervention in a problem construction task 1 Mar 2016 | Thinking Skills and Creativity, Vol. 19
- A Belief System at the Core of Learning Science 1 Jan 2016
- Science and Innovative Thinking for Technical and Organizational Development 1 Jan 2016
- Student Research Work and Modeled Situations in Order to Bridge the Gap between Basic Science Concepts and Those from Preventive and Clinical Practice. Meaningful Learning and Informed beneficience 1 Jan 2016 | Creative Education, Vol. 07, No. 07
- FOSTERING FIFTH GRADERS’ SCIENTIFIC CREATIVITY THROUGH PROBLEM-BASED LEARNING 25 October 2015 | Journal of Baltic Science Education, Vol. 14, No. 5
- Scaffolding for Creative Product Possibilities in a Design-Based STEM Activity 16 November 2014 | Research in Science Education, Vol. 45, No. 5
- Intuition and insight: two concepts that illuminate the tacit in science education 18 June 2015 | Studies in Science Education, Vol. 51, No. 2
- Arts and crafts as adjuncts to STEM education to foster creativity in gifted and talented students 28 March 2015 | Asia Pacific Education Review, Vol. 16, No. 2
- Initiatives Towards an Education for Creativity 1 May 2015 | Procedia - Social and Behavioral Sciences, Vol. 180
- Brian A. Couch ,
- Tanya L. Brown ,
- Tyler J. Schelpat ,
- Mark J. Graham , and
- Jennifer K. Knight
- Michèle Shuster, Monitoring Editor
- Kim Quillin , and
- Stephen Thomas
- Mary Lee Ledbetter, Monitoring Editor
- The Design of IdeaWorks: Applying Social Learning Networks to Support Tertiary Education 21 July 2015
- References 1 Jan 2015
- Video Games and Malevolent Creativity 1 Jan 2015
- Modelling a Laboratory for Ideas as a New Tool for Fostering Engineering Creativity 1 Jan 2015 | Procedia Engineering, Vol. 100
- “Development of Thinking Skills” Course: Teaching TRIZ in Academic Setting 1 Jan 2015 | Procedia Engineering, Vol. 131
- Leadership in the Future Experts’ Creativity Development with Scientific Research Activities 4 November 2014
- Developing Deaf Children's Conceptual Understanding and Scientific Argumentation Skills: A Literature Review 3 January 2014 | Deafness & Education International, Vol. 16, No. 3
- Leslie M. Stevens , and
- Sally G. Hoskins
- Nancy Pelaez, Monitoring Editor
- 2014 | Cortex, Vol. 51
- A Sociotechnological Theory of Discursive Change and Entrepreneurial Capacity: Novelty and Networks 1 Jan 2014 | SSRN Electronic Journal, Vol. 3
- GEOverse: An Undergraduate Research Journal: Research Dissemination Within and Beyond the Curriculum 1 August 2013
- Learning by Practice, High-Pressure Student Ateliers 2 August 2013
- Relating Inter-Individual Differences in Verbal Creative Thinking to Cerebral Structures: An Optimal Voxel-Based Morphometry Study 5 November 2013 | PLoS ONE, Vol. 8, No. 11
- 21st Century Biology: An Interdisciplinary Approach of Biology, Technology, Engineering and Mathematics Education 1 Nov 2013 | Procedia - Social and Behavioral Sciences, Vol. 102
- Reclaiming creativity in the era of impact: exploring ideas about creative research in science and engineering 1 Nov 2013 | Studies in Higher Education, Vol. 38, No. 9
- An Evaluation of Alternative Ways of Computing the Creativity Quotient in a Design School Sample 1 Jul 2013 | Creativity Research Journal, Vol. 25, No. 3
- A.-M. Hoskinson ,
- M. D. Caballero , and
- J. K. Knight
- Eric Brewe, Monitoring Editor
- Understanding, attitude and environment 17 May 2013 | International Journal for Researcher Development, Vol. 4, No. 1
- Promoting Student Creativity and Inventiveness in Science and Engineering 1 Jan 2013
- Building creative thinking in the classroom: From research to practice 1 Jan 2013 | International Journal of Educational Research, Vol. 62
- A Demonstration of a Mastery Goal Driven Learning Environment to Foster Creativity in Engineering Design 1 Jan 2013 | SSRN Electronic Journal, Vol. 111
- The development of creative cognition across adolescence: distinct trajectories for insight and divergent thinking 8 October 2012 | Developmental Science, Vol. 16, No. 1
- A CROSS-NATIONAL STUDY OF PROSPECTIVE ELEMENTARY AND SCIENCE TEACHERS’ CREATIVITY STYLES 10 September 2012 | Journal of Baltic Science Education, Vol. 11, No. 3
- Evaluation of fostering students' creativity in preparing aided recalls for revision courses using electronic revision and recapitulation tools 2.0 1 Aug 2012 | Behaviour & Information Technology, Vol. 31, No. 8
- Scientific Creativity: The Missing Ingredient in Slovenian Science Education 15 April 2012 | European Journal of Educational Research, Vol. volume-1-2012, No. volume1-issue2.html
- Could the ‘evolution’ from biology to life sciences prevent ‘extinction’ of the subject field? 6 March 2012 | Suid-Afrikaanse Tydskrif vir Natuurwetenskap en Tegnologie, Vol. 31, No. 1
- Mobile innovations, executive functions, and educational developments in conflict zones: a case study from Palestine 1 October 2011 | Educational Technology Research and Development, Vol. 60, No. 1
- Informing Pedagogy Through the Brain-Targeted Teaching Model 1 Jan 2012 | Journal of Microbiology & Biology Education, Vol. 13, No. 1
- Teaching Creative Science Thinking 16 Dec 2011 | Science, Vol. 334, No. 6062
- Sally G. Hoskins ,
- David Lopatto , and
- Leslie M. Stevens
- Diane K. O'Dowd, Monitoring Editor
- Embedding Research-Based Learning Early in the Undergraduate Geography Curriculum 1 Aug 2011 | Journal of Geography in Higher Education, Vol. 35, No. 3
- Jared L. Taylor ,
- Karen M. Smith ,
- Adrian P. van Stolk , and
- George B. Spiegelman
- Debra Tomanek, Monitoring Editor
- 2010 | IFAC Proceedings Volumes, Vol. 43, No. 17
- Critical and Creative Thinking Activities for Engaged Learning in Graphics and Visualization Course
- Creativity Development through Inquiry-Based Learning in Biomedical Sciences
Submitted: 31 December 2008 Revised: 14 May 2009 Accepted: 28 May 2009 © 2009 by The American Society for Cell Biology  An official website of the United States government The .gov means it’s official. Federal government websites often end in .gov or .mil. Before sharing sensitive information, make sure you’re on a federal government site. The site is secure. The https:// ensures that you are connecting to the official website and that any information you provide is encrypted and transmitted securely. - Publications
- Account settings
Preview improvements coming to the PMC website in October 2024. Learn More or Try it out now . - Advanced Search
- Journal List
 Identifying problems and solutions in scientific textKevin heffernan. Department of Computer Science and Technology, University of Cambridge, 15 JJ Thomson Avenue, Cambridge, CB3 0FD UK Simone TeufelResearch is often described as a problem-solving activity, and as a result, descriptions of problems and solutions are an essential part of the scientific discourse used to describe research activity. We present an automatic classifier that, given a phrase that may or may not be a description of a scientific problem or a solution, makes a binary decision about problemhood and solutionhood of that phrase. We recast the problem as a supervised machine learning problem, define a set of 15 features correlated with the target categories and use several machine learning algorithms on this task. We also create our own corpus of 2000 positive and negative examples of problems and solutions. We find that we can distinguish problems from non-problems with an accuracy of 82.3%, and solutions from non-solutions with an accuracy of 79.7%. Our three most helpful features for the task are syntactic information (POS tags), document and word embeddings. IntroductionProblem solving is generally regarded as the most important cognitive activity in everyday and professional contexts (Jonassen 2000 ). Many studies on formalising the cognitive process behind problem-solving exist, for instance (Chandrasekaran 1983 ). Jordan ( 1980 ) argues that we all share knowledge of the thought/action problem-solution process involved in real life, and so our writings will often reflect this order. There is general agreement amongst theorists that state that the nature of the research process can be viewed as a problem-solving activity (Strübing 2007 ; Van Dijk 1980 ; Hutchins 1977 ; Grimes 1975 ). One of the best-documented problem-solving patterns was established by Winter ( 1968 ). Winter analysed thousands of examples of technical texts, and noted that these texts can largely be described in terms of a four-part pattern consisting of Situation, Problem, Solution and Evaluation. This is very similar to the pattern described by Van Dijk ( 1980 ), which consists of Introduction-Theory, Problem-Experiment-Comment and Conclusion. The difference is that in Winter’s view, a solution only becomes a solution after it has been evaluated positively. Hoey changes Winter’s pattern by introducing the concept of Response in place of Solution (Hoey 2001 ). This seems to describe the situation in science better, where evaluation is mandatory for research solutions to be accepted by the community. In Hoey’s pattern, the Situation (which is generally treated as optional) provides background information; the Problem describes an issue which requires attention; the Response provides a way to deal with the issue, and the Evaluation assesses how effective the response is. An example of this pattern in the context of the Goldilocks story can be seen in Fig. 1 . In this text, there is a preamble providing the setting of the story (i.e. Goldilocks is lost in the woods), which is called the Situation in Hoey’s system. A Problem in encountered when Goldilocks becomes hungry. Her first Response is to try the porridge in big bear’s bowl, but she gives this a negative Evaluation (“too hot!”) and so the pattern returns to the Problem. This continues in a cyclic fashion until the Problem is finally resolved by Goldilocks giving a particular Response a positive Evaluation of baby bear’s porridge (“it’s just right”).  Example of problem-solving pattern when applied to the Goldilocks story. Reproduced with permission from Hoey ( 2001 ) It would be attractive to detect problem and solution statements automatically in text. This holds true both from a theoretical and a practical viewpoint. Theoretically, we know that sentiment detection is related to problem-solving activity, because of the perception that “bad” situations are transformed into “better” ones via problem-solving. The exact mechanism of how this can be detected would advance the state of the art in text understanding. In terms of linguistic realisation, problem and solution statements come in many variants and reformulations, often in the form of positive or negated statements about the conditions, results and causes of problem–solution pairs. Detecting and interpreting those would give us a reasonably objective manner to test a system’s understanding capacity. Practically, being able to detect any mention of a problem is a first step towards detecting a paper’s specific research goal. Being able to do this has been a goal for scientific information retrieval for some time, and if successful, it would improve the effectiveness of scientific search immensely. Detecting problem and solution statements of papers would also enable us to compare similar papers and eventually even lead to automatic generation of review articles in a field. There has been some computational effort on the task of identifying problem-solving patterns in text. However, most of the prior work has not gone beyond the usage of keyword analysis and some simple contextual examination of the pattern. Flowerdew ( 2008 ) presents a corpus-based analysis of lexio-grammatical patterns for problem and solution clauses using articles from professional and student reports. Problem and solution keywords were used to search their corpora, and each occurrence was analysed to determine grammatical usage of the keyword. More interestingly, the causal category associated with each keyword in their context was also analysed. For example, Reason–Result or Means-Purpose were common causal categories found to be associated with problem keywords. The goal of the work by Scott ( 2001 ) was to determine words which are semantically similar to problem and solution, and to determine how these words are used to signal problem-solution patterns. However, their corpus-based analysis used articles from the Guardian newspaper. Since the domain of newspaper text is very different from that of scientific text, we decided not to consider those keywords associated with problem-solving patterns for use in our work. Instead of a keyword-based approach, Charles ( 2011 ) used discourse markers to examine how the problem-solution pattern was signalled in text. In particular, they examined how adverbials associated with a result such as “thus, therefore, then, hence” are used to signal a problem-solving pattern. Problem solving also has been studied in the framework of discourse theories such as Rhetorical Structure Theory (Mann and Thompson 1988 ) and Argumentative Zoning (Teufel et al. 2000 ). Problem- and solutionhood constitute two of the original 23 relations in RST (Mann and Thompson 1988 ). While we concentrate solely on this aspect, RST is a general theory of discourse structure which covers many intentional and informational relations. The relationship to Argumentative Zoning is more complicated. The status of certain statements as problem or solutions is one important dimension in the definitions of AZ categories. AZ additionally models dimensions other than problem-solution hood (such as who a scientific idea belongs to, or which intention the authors might have had in stating a particular negative or positive statement). When forming categories, AZ combines aspects of these dimensions, and “flattens” them out into only 7 categories. In AZ it is crucial who it is that experiences the problems or contributes a solution. For instance, the definition of category “CONTRAST” includes statements that some research runs into problems, but only if that research is previous work (i.e., not if it is the work contributed in the paper itself). Similarly, “BASIS” includes statements of successful problem-solving activities, but only if they are achieved by previous work that the current paper bases itself on. Our definition is simpler in that we are interested only in problem solution structure, not in the other dimensions covered in AZ. Our definition is also more far-reaching than AZ, in that we are interested in all problems mentioned in the text, no matter whose problems they are. Problem-solution recognition can therefore be seen as one aspect of AZ which can be independently modelled as a “service task”. This means that good problem solution structure recognition should theoretically improve AZ recognition. In this work, we approach the task of identifying problem-solving patterns in scientific text. We choose to use the model of problem-solving described by Hoey ( 2001 ). This pattern comprises four parts: Situation, Problem, Response and Evaluation. The Situation element is considered optional to the pattern, and so our focus centres on the core pattern elements. Goal statement and taskMany surface features in the text offer themselves up as potential signals for detecting problem-solving patterns in text. However, since Situation is an optional element, we decided to focus on either Problem or Response and Evaluation as signals of the pattern. Moreover, we decide to look for each type in isolation. Our reasons for this are as follows: It is quite rare for an author to introduce a problem without resolving it using some sort of response, and so this is a good starting point in identifying the pattern. There are exceptions to this, as authors will sometimes introduce a problem and then leave it to future work, but overall there should be enough signal in the Problem element to make our method of looking for it in isolation worthwhile. The second signal we look for is the use of Response and Evaluation within the same sentence. Similar to Problem elements, we hypothesise that this formulation is well enough signalled externally to help us in detecting the pattern. For example, consider the following Response and Evaluation: “One solution is to use smoothing”. In this statement, the author is explicitly stating that smoothing is a solution to a problem which must have been mentioned in a prior statement. In scientific text, we often observe that solutions implicitly contain both Response and Evaluation (positive) elements. Therefore, due to these reasons there should be sufficient external signals for the two pattern elements we concentrate on here. When attempting to find Problem elements in text, we run into the issue that the word “problem” actually has at least two word senses that need to be distinguished. There is a word sense of “problem” that means something which must be undertaken (i.e. task), while another sense is the core sense of the word, something that is problematic and negative. Only the latter sense is aligned with our sense of problemhood. This is because the simple description of a task does not predispose problemhood, just a wish to perform some act. Consider the following examples, where the non-desired word sense is being used: - “Das and Petrov (2011) also consider the problem of unsupervised bilingual POS induction”. (Chen et al. 2011 ).
- “In this paper, we describe advances on the problem of NER in Arabic Wikipedia”. (Mohit et al. 2012 ).
Here, the author explicitly states that the phrases in orange are problems, they align with our definition of research tasks and not with what we call here ‘problematic problems’. We will now give some examples from our corpus for the desired, core word sense: - “The major limitation of supervised approaches is that they require annotations for example sentences.” (Poon and Domingos 2009 ).
- “To solve the problem of high dimensionality we use clustering to group the words present in the corpus into much smaller number of clusters”. (Saha et al. 2008 ).
When creating our corpus of positive and negative examples, we took care to select only problem strings that satisfy our definition of problemhood; “ Corpus creation ” section will explain how we did that. Corpus creationOur new corpus is a subset of the latest version of the ACL anthology released in March, 2016 1 which contains 22,878 articles in the form of PDFs and OCRed text. 2 The 2016 version was also parsed using ParsCit (Councill et al. 2008 ). ParsCit recognises not only document structure, but also bibliography lists as well as references within running text. A random subset of 2500 papers was collected covering the entire ACL timeline. In order to disregard non-article publications such as introductions to conference proceedings or letters to the editor, only documents containing abstracts were considered. The corpus was preprocessed using tokenisation, lemmatisation and dependency parsing with the Rasp Parser (Briscoe et al. 2006 ). Definition of ground truthOur goal was to define a ground truth for problem and solution strings, while covering as wide a range as possible of syntactic variations in which such strings naturally occur. We also want this ground truth to cover phenomena of problem and solution status which are applicable whether or not the problem or solution status is explicitly mentioned in the text. To simplify the task, we only consider here problem and solution descriptions that are at most one sentence long. In reality, of course, many problem descriptions and solution descriptions go beyond single sentence, and require for instance an entire paragraph. However, we also know that short summaries of problems and solutions are very prevalent in science, and also that these tend to occur in the most prominent places in a paper. This is because scientists are trained to express their contribution and the obstacles possibly hindering their success, in an informative, succinct manner. That is the reason why we can afford to only look for shorter problem and solution descriptions, ignoring those that cross sentence boundaries. To define our ground truth, we examined the parsed dependencies and looked for a target word (“problem/solution”) in subject position, and then chose its syntactic argument as our candidate problem or solution phrase. To increase the variation, i.e., to find as many different-worded problem and solution descriptions as possible, we additionally used semantically similar words (near-synonyms) of the target words “problem” or “solution” for the search. Semantic similarity was defined as cosine in a deep learning distributional vector space, trained using Word2Vec (Mikolov et al. 2013 ) on 18,753,472 sentences from a biomedical corpus based on all full-text Pubmed articles (McKeown et al. 2016 ). From the 200 words which were semantically closest to “problem”, we manually selected 28 clear synonyms. These are listed in Table 1 . From the 200 semantically closest words to “solution” we similarly chose 19 (Table 2 ). Of the sentences matching our dependency search, a subset of problem and solution candidate sentences were randomly selected. Selected words for use in problem candidate phrase extraction | Bottleneck | Caveat | Challenge | Complication | Conundrum | Difficulty | | Flaw | Impediment | Issue | Limitation | Mistake | Obstacle | | Riddle | Shortcoming | Struggle | Subproblem | Threat | Tragedy | | Dilemma | Disadvantage | Drawback | Fault | Pitfall | Problem | | Uncertainty | Weakness | Trouble | Quandary | | |
Selected words for use in solution candidate phrase extraction | Solution | Alternative | Suggestion | Idea | Way | Proposal | | Technique | Remedy | Task | Step | Answer | Approach | | Approaches | Strategy | Method | Methodology | Scheme | Answers | | Workaround | | | | | |
An example of this is shown in Fig. 2 . Here, the target word “drawback” is in subject position (highlighted in red), and its clausal argument (ccomp) is “(that) it achieves low performance” (highlighted in purple). Examples of other arguments we searched for included copula constructions and direct/indirect objects.  Example of our extraction method for problems using dependencies. (Color figure online) If more than one candidate was found in a sentence, one was chosen at random. Non-grammatical sentences were excluded; these might appear in the corpus as a result of its source being OCRed text. 800 candidates phrases expressing problems and solutions were automatically extracted (1600 total) and then independently checked for correctness by two annotators (the two authors of this paper). Both authors found the task simple and straightforward. Correctness was defined by two criteria: - An unexplained phenomenon or a problematic state in science; or
- A research question; or
- An artifact that does not fulfil its stated specification.
- The phrase must not lexically give away its status as problem or solution phrase.
The second criterion saves us from machine learning cues that are too obvious. If for instance, the phrase itself contained the words “lack of” or “problematic” or “drawback”, our manual check rejected it, because it would be too easy for the machine learner to learn such cues, at the expense of many other, more generally occurring cues. Sampling of negative examplesWe next needed to find negative examples for both cases. We wanted them not to stand out on the surface as negative examples, so we chose them so as to mimic the obvious characteristics of the positive examples as closely as possible. We call the negative examples ‘non-problems’ and ‘non-solutions’ respectively. We wanted the only differences between problems and non-problems to be of a semantic nature, nothing that could be read off on the surface. We therefore sampled a population of phrases that obey the same statistical distribution as our problem and solution strings while making sure they really are negative examples. We started from sentences not containing any problem/solution words (i.e. those used as target words). From each such sentence, we at random selected one syntactic subtree contained in it. From these, we randomly selected a subset of negative examples of problems and solutions that satisfy the following conditions: - The distribution of the head POS tags of the negative strings should perfectly match the head POS tags 3 of the positive strings. This has the purpose of achieving the same proportion of surface syntactic constructions as observed in the positive cases.
- The average lengths of the negative strings must be within a tolerance of the average length of their respective positive candidates e.g., non-solutions must have an average length very similar (i.e. + / - small tolerance) to solutions. We chose a tolerance value of 3 characters.
Again, a human quality check was performed on non-problems and non-solutions. For each candidate non-problem statement, the candidate was accepted if it did not contain a phenomenon, a problematic state, a research question or a non-functioning artefact. If the string expressed a research task, without explicit statement that there was anything problematic about it (i.e., the ‘wrong’ sense of “problem”, as described above), it was allowed as a non-problem. A clause was confirmed as a non-solution if the string did not represent both a response and positive evaluation. If the annotator found that the sentence had been slightly mis-parsed, but did contain a candidate, they were allowed to move the boundaries for the candidate clause. This resulted in cleaner text, e.g., in the frequent case of coordination, when non-relevant constituents could be removed. From the set of sentences which passed the quality-test for both independent assessors, 500 instances of positive and negative problems/solutions were randomly chosen (i.e. 2000 instances in total). When checking for correctness we found that most of the automatically extracted phrases which did not pass the quality test for problem-/solution-hood were either due to obvious learning cues or instances where the sense of problem-hood used is relating to tasks (cf. “ Goal statement and task ” section). Experimental designIn our experiments, we used three classifiers, namely Naïve Bayes, Logistic Regression and a Support Vector Machine. For all classifiers an implementation from the WEKA machine learning library (Hall et al. 2009 ) was chosen. Given that our dataset is small, tenfold cross-validation was used instead of a held out test set. All significance tests were conducted using the (two-tailed) Sign Test (Siegel 1956 ). Linguistic correlates of problem- and solution-hoodWe first define a set of features without taking the phrase’s context into account. This will tell us about the disambiguation ability of the problem/solution description’s semantics alone. In particular, we cut out the rest of the sentence other than the phrase and never use it for classification. This is done for similar reasons to excluding certain ‘give-away’ phrases inside the phrases themselves (as explained above). As the phrases were found using templates, we know that the machine learner would simply pick up on the semantics of the template, which always contains a synonym of “problem” or “solution”, thus drowning out the more hidden features hopefully inherent in the semantics of the phrases themselves. If we allowed the machine learner to use these stronger features, it would suffer in its ability to generalise to the real task. ngrams Bags of words are traditionally successfully used for classification tasks in NLP, so we included bags of words (lemmas) within the candidate phrases as one of our features (and treat it as a baseline later on). We also include bigrams and trigrams as multi-word combinations can be indicative of problems and solutions e.g., “combinatorial explosion”. Polarity Our second feature concerns the polarity of each word in the candidate strings. Consider the following example of a problem taken from our dataset: “very conservative approaches to exact and partial string matches overgenerate badly”. In this sentence, words such as “badly” will be associated with negative polarity, therefore being useful in determining problem-hood. Similarly, solutions will often be associated with a positive sentiment e.g. “smoothing is a good way to overcome data sparsity” . To do this, we perform word sense disambiguation of each word using the Lesk algorithm (Lesk 1986 ). The polarity of the resulting synset in SentiWordNet (Baccianella et al. 2010 ) was then looked up and used as a feature. Syntax Next, a set of syntactic features were defined by using the presence of POS tags in each candidate. This feature could be helpful in finding syntactic patterns in problems and solutions. We were careful not to base the model directly on the head POS tag and the length of each candidate phrase, as these are defining characteristics used for determining the non-problem and non-solution candidate set. Negation Negation is an important property that can often greatly affect the polarity of a phrase. For example, a phrase containing a keyword pertinent to solution-hood may be a good indicator but with the presence of negation may flip the polarity to problem-hood e.g., “this can’t work as a solution”. Therefore, presence of negation is determined. Exemplification and contrast Problems and solutions are often found to be coupled with examples as they allow the author to elucidate their point. For instance, consider the following solution: “Once the translations are generated, an obvious solution is to pick the most fluent alternative, e.g., using an n-gram language model”. (Madnani et al. 2012 ). To acknowledge this, we check for presence of exemplification. In addition to examples, problems in particular are often found when contrast is signalled by the author (e.g. “however, “but”), therefore we also check for presence of contrast in the problem and non-problem candidates only. Discourse Problems and solutions have also been found to have a correlation with discourse properties. For example, problem-solving patterns often occur in the background sections of a paper. The rationale behind this is that the author is conventionally asked to objectively criticise other work in the background (e.g. describing research gaps which motivate the current paper). To take this in account, we examine the context of each string and capture the section header under which it is contained (e.g. Introduction, Future work). In addition, problems and solutions are often found following the Situation element in the problem-solving pattern (cf. “ Introduction ” section). This preamble setting up the problem or solution means that these elements are likely not to be found occurring at the beginning of a section (i.e. it will usually take some sort of introduction to detail how something is problematic and why a solution is needed). Therefore we record the distance from the candidate string to the nearest section header. Subcategorisation and adverbials Solutions often involve an activity (e.g. a task). We also model the subcategorisation properties of the verbs involved. Our intuition was that since problematic situations are often described as non-actions, then these are more likely to be intransitive. Conversely solutions are often actions and are likely to have at least one argument. This feature was calculated by running the C&C parser (Curran et al. 2007 ) on each sentence. C&C is a supertagger and parser that has access to subcategorisation information. Solutions are also associated with resultative adverbial modification (e.g. “thus, therefore, consequently”) as it expresses the solutionhood relation between the problem and the solution. It has been seen to occur frequently in problem-solving patterns, as studied by Charles ( 2011 ). Therefore, we check for presence of resultative adverbial modification in the solution and non-solution candidate only. Embeddings We also wanted to add more information using word embeddings. This was done in two different ways. Firstly, we created a Doc2Vec model (Le and Mikolov 2014 ), which was trained on ∼ 19 million sentences from scientific text (no overlap with our data set). An embedding was created for each candidate sentence. Secondly, word embeddings were calculated using the Word2Vec model (cf. “ Corpus creation ” section). For each candidate head, the full word embedding was included as a feature. Lastly, when creating our polarity feature we query SentiWordNet using synsets assigned by the Lesk algorithm. However, not all words are assigned a sense by Lesk, so we need to take care when that happens. In those cases, the distributional semantic similarity of the word is compared to two words with a known polarity, namely “poor” and “excellent”. These particular words have traditionally been consistently good indicators of polarity status in many studies (Turney 2002 ; Mullen and Collier 2004 ). Semantic similarity was defined as cosine similarity on the embeddings of the Word2Vec model (cf. “ Corpus creation ” section). Modality Responses to problems in scientific writing often express possibility and necessity, and so have a close connection with modality. Modality can be broken into three main categories, as described by Kratzer ( 1991 ), namely epistemic (possibility), deontic (permission / request / wish) and dynamic (expressing ability). Problems have a strong relationship to modality within scientific writing. Often, this is due to a tactic called “hedging” (Medlock and Briscoe 2007 ) where the author uses speculative language, often using Epistemic modality, in an attempt to make either noncommital or vague statements. This has the effect of allowing the author to distance themselves from the statement, and is often employed when discussing negative or problematic topics. Consider the following example of Epistemic modality from Nakov and Hearst ( 2008 ): “A potential drawback is that it might not work well for low-frequency words”. To take this linguistic correlate into account as a feature, we replicated a modality classifier as described by (Ruppenhofer and Rehbein 2012 ). More sophisticated modality classifiers have been recently introduced, for instance using a wide range of features and convolutional neural networks, e.g, (Zhou et al. 2015 ; Marasović and Frank 2016 ). However, we wanted to check the effect of a simpler method of modality classification on the final outcome first before investing heavily into their implementation. We trained three classifiers using the subset of features which Ruppenhofer et al. reported as performing best, and evaluated them on the gold standard dataset provided by the authors 4 . The results of the are shown in Table 3 . The dataset contains annotations of English modal verbs on the 535 documents of the first MPQA corpus release (Wiebe et al. 2005 ). Modality classifier results (precision/recall/f-measure) using Naïve Bayes (NB), logistic regression, and a support vector machine (SVM) | Modality | Classification accuracy |
|---|
| NB | LR | SVM |
|---|
| Epistemic | .74/.74/.74 | | .75/.85/.80 | | Deontic | .94/.72/.81 | | .86/.81/.83 | | Dynamic | | | .69/.70/.70 |
Italicized results reflect highest f-measure reported per modal category Logistic Regression performed best overall and so this model was chosen for our upcoming experiments. With regards to the optative and concessive modal categories, they can be seen to perform extremely poorly, with the optative category receiving a null score across all three classifiers. This is due to a limitation in the dataset, which is unbalanced and contains very few instances of these two categories. This unbalanced data also is the reason behind our decision of reporting results in terms of recall, precision and f-measure in Table 3 . The modality classifier was then retrained on the entirety of the dataset used by Ruppenhofer and Rehbein ( 2012 ) using the best performing model from training (Logistic Regression). This new model was then used in the upcoming experiment to predict modality labels for each instance in our dataset. As can be seen from Table 4 , we are able to achieve good results for distinguishing a problematic statement from non-problematic one. The bag-of-words baseline achieves a very good performance of 71.0% for the Logistic Regression classifier, showing that there is enough signal in the candidate phrases alone to distinguish them much better than random chance. Results distinguishing problems from non-problems using Naïve Bayes (NB), logistic regression (LR) and a support vector machine (SVM) | Feature sets | Classification accuracy |
|---|
| NB | SVM | LR |
|---|
| 1 | Baseline | 65.6 | 67.8 | 71.0 | | 2 | Bigrams | 61.3 | 60.5 | 59.0 | | 3 | Contrast | 50.6 | 50.8 | 50.5 | | 4 | Discourse | 60.3 | 60.2 | 60.0 | | 5 | Doc2vec | 72.9* | 72.7 | 72.3 | | 6 | Exemplification | 50.3 | 50.2 | 50.0 | | 7 | Modality | 52.3 | 52.3 | 50.3 | | 8 | Negation | 59.9 | 59.9 | 59.9 | | 9 | Polarity | 60.2 | 66.3 | 65.5 | | 10 | Syntax | 73.6* | 76.2** | 74.4 | | 11 | Subcategorisation | 46.9 | 47.3 | 49.1 | | 12 | Trigrams | 57.7 | 51.2 | 54.0 | | 13 | Word2vec | 57.9 | 64.1 | 64.7 | | 14 | Word2vec | 76.2*** | 77.2** | 76.6 | | 15 | All features | 79.3*** | 81.8*** | ** | | 16 | All features-{2,3,7,12} | | | 79.0** |
Each feature set’s performance is shown in isolation followed by combinations with other features. Tenfold stratified cross-validation was used across all experiments. Statistical significance with respect to the baseline at the p < 0.05 , 0.01, 0.001 levels is denoted by *, ** and *** respectively Taking a look at Table 5 , which shows the information gain for the top lemmas, Information gain (IG) in bits of top lemmas from the bag-of-words baseline in Table 4 | IG | Features |
|---|
| 0.048 | Not | | 0.019 | Do | | 0.018 | Single | | 0.013 | Limited, experiment | | 0.010 | Data, information | | 0.009 | Error, many | | 0.008 | Take, explosion |
we can see that the top lemmas are indeed indicative of problemhood (e.g. “limit”,“explosion”). Bigrams achieved good performance on their own (as did negation and discourse) but unfortunately performance deteriorated when using trigrams, particularly with the SVM and LR. The subcategorisation feature was the worst performing feature in isolation. Upon taking a closer look at our data, we saw that our hypothesis that intransitive verbs are commonly used in problematic statements was true, with over 30% of our problems (153) using them. However, due to our sampling method for the negative cases we also picked up many intransitive verbs (163). This explains the almost random chance performance (i.e. 50%) given that the distribution of intransitive verbs amongst the positive and negative candidates was almost even. The modality feature was the most expensive to produce, but also didn’t perform very well is isolation. This surprising result may be partly due to a data sparsity issue where only a small portion (169) of our instances contained modal verbs. The breakdown of how many types of modal senses which occurred is displayed in Table 6 . The most dominant modal sense was epistemic. This is a good indicator of problemhood (e.g. hedging, cf. “ Linguistic correlates of problem- and solution-hood ” section) but if the accumulation of additional data was possible, we think that this feature may have the potential to be much more valuable in determining problemhood. Another reason for the performance may be domain dependence of the classifier since it was trained on text from different domains (e.g. news). Additionally, modality has also shown to be helpful in determining contextual polarity (Wilson et al. 2005 ) and argumentation (Becker et al. 2016 ), so using the output from this modality classifier may also prove useful for further feature engineering taking this into account in future work. Number of instances of modal senses | No. of instances |
|---|
| Epistemic | 97 | | Deontic | 22 | | Dynamic | 50 |
Polarity managed to perform well but not as good as we hoped. However, this feature also suffers from a sparsity issue resulting from cases where the Lesk algorithm (Lesk 1986 ) is not able to resolve the synset of the syntactic head. Knowledge of syntax provides a big improvement with a significant increase over the baseline results from two of the classifiers. Examining this in greater detail, POS tags with high information gain mostly included tags from open classes (i.e. VB-, JJ-, NN- and RB-). These tags are often more associated with determining polarity status than tags such as prepositions and conjunctions (i.e. adverbs and adjectives are more likely to be describing something with a non-neutral viewpoint). The embeddings from Doc2Vec allowed us to obtain another significant increase in performance (72.9% with Naïve Bayes) over the baseline and polarity using Word2Vec provided the best individual feature result (77.2% with SVM). Combining all features together, each classifier managed to achieve a significant result over the baseline with the best result coming from the SVM (81.8%). Problems were also better classified than non-problems as shown in the confusion matrix in Table 7 . The addition of the Word2Vec vectors may be seen as a form of smoothing in cases where previous linguistic features had a sparsity issue i.e., instead of a NULL entry, the embeddings provide some sort of value for each candidate. Particularly wrt. the polarity feature, cases where Lesk was unable to resolve a synset meant that a ZERO entry was added to the vector supplied to the machine learner. Amongst the possible combinations, the best subset of features was found by combining all features with the exception of bigrams, trigrams, subcategorisation and modality. This subset of features managed to improve results in both the Naïve Bayes and SVM classifiers with the highest overall result coming from the SVM (82.3%). Confusion matrix for problems | Predicted |
|---|
| Problem | Non-problem |
|---|
| Actual | | Problem | 414 | 86 | | Non-problem | 91 | 409 |
The results for disambiguation of solutions from non-solutions can be seen in Table 8 . The bag-of-words baseline performs much better than random, with the performance being quite high with regard to the SVM (this result was also higher than any of the baseline performances from the problem classifiers). As shown in Table 9 , the top ranked lemmas from the best performing model (using information gain) included “use” and “method”. These lemmas are very indicative of solutionhood and so give some insight into the high baseline returned from the machine learners. Subcategorisation and the result adverbials were the two worst performing features. However, the low performance for subcategorisation is due to the sampling of the non-solutions (the same reason for the low performance of the problem transitivity feature). When fitting the POS-tag distribution for the negative samples, we noticed that over 80% of the head POS-tags were verbs (much higher than the problem heads). The most frequent verb type being the infinite form. Results distinguishing solutions from non-solutions using Naïve Bayes (NB), logistic regression (LR) and a support vector machine (SVM) | Feature sets | Classification accuracy |
|---|
| NB | SVM | LR |
|---|
| 1 | Baseline | 72.5 | 73.6 | 70.7 | | 2 | Adverbial of result | 48.3 | 50.5 | 50.3 | | 3 | Bigrams | 63.1 | 65.1 | 59.8 | | 4 | Discourse | 56.9 | 56.4 | 58.2 | | 5 | Doc2vec | 65.9 | 68.7 | 67.7 | | 6 | Exemplification | 63.1 | 65.1 | 59.8 | | 7 | Negation | 63.1 | 65.1 | 59.8 | | 8 | Polarity | 63.1 | 65.1 | 59.8 | | 9 | Subcategorisation | 55.4 | 53.3 | 55.3 | | 10 | Syntax | 61.9 | 62.2 | 64.4 | | 11 | Trigrams | 63.1 | 65.1 | 59.8 | | 12 | Word2vec | 68.2 | 70.7 | 68.9 | | 13 | Word2vec | 72.1 | 73.4 | 69.4 | | 14 | All features | | 79.5 | 73.1 | | 15 | All features-{2,3,6,7,8,13} | 73.8 | | |
Each feature set’s performance is shown in isolation followed by combinations with other features. Tenfold stratified cross-validation was used across all experiments Information gain (IG) in bits of top lemmas from the bag-of-words baseline in Table 8 | IG | Features |
|---|
| 0.076 | Be | | 0.047 | Use | | 0.014 | Method | | 0.013 | Argument | | 0.012 | Dependency | | 0.011 | Configuration, sequence, subject | | 0.009 | Label, weakest | | 0.008 | Following, edge, employ |
This is not surprising given that a very common formulation to describe a solution is to use the infinitive “TO” since it often describes a task e.g., “One solution is to find the singletons and remove them”. Therefore, since the head POS tags of the non-solutions had to match this high distribution of infinitive verbs present in the solution, the subcategorisation feature is not particularly discriminatory. Polarity, negation, exemplification and syntactic features were slightly more discriminate and provided comparable results. However, similar to the problem experiment, the embeddings from Word2Vec and Doc2Vec proved to be the best features, with polarity using Word2Vec providing the best individual result (73.4% with SVM). Combining all features together managed to improve over each feature in isolation and beat the baseline using all three classifiers. Furthermore, when looking at the confusion matrix in Table 10 the solutions were classified more accurately than the non-solutions. The best subset of features was found by combining all features without adverbial of result, bigrams, exemplification, negation, polarity and subcategorisation. The best result using this subset of features was achieved by the SVM with 79.7%. It managed to greatly improve upon the baseline but was just shy of achieving statistical significance ( p = 0.057 ). Confusion matrix for solutions | Predicted |
|---|
| Solution | Non-solution |
|---|
| Actual | | Solution | 411 | 89 | | Non-solution | 114 | 386 |
In this work, we have presented new supervised classifiers for the task of identifying problem and solution statements in scientific text. We have also introduced a new corpus for this task and used it for evaluating our classifiers. Great care was taken in constructing the corpus by ensuring that the negative and positive samples were closely matched in terms of syntactic shape. If we had simply selected random subtrees for negative samples without regard for any syntactic similarity with our positive samples, the machine learner may have found easy signals such as sentence length. Additionally, since we did not allow the machine learner to see the surroundings of the candidate string within the sentence, this made our task even harder. Our performance on the corpus shows promise for this task, and proves that there are strong signals for determining both the problem and solution parts of the problem-solving pattern independently. With regard to classifying problems from non-problems, features such as the POS tag, document and word embeddings provide the best features, with polarity using the Word2Vec embeddings achieving the highest feature performance. The best overall result was achieved using an SVM with a subset of features (82.3%). Classifying solutions from non-solutions also performs well using the embedding features, with the best feature also being polarity using the Word2Vec embeddings, and the highest result also coming from the SVM with a feature subset (79.7%). In future work, we plan to link problem and solution statements which were found independently during our corpus creation. Given that our classifiers were trained on data solely from the ACL anthology, we also hope to investigate the domain specificity of our classifiers and see how well they can generalise to domains other than ACL (e.g. bioinformatics). Since we took great care at removing the knowledge our classifiers have of the explicit statements of problem and solution (i.e. the classifiers were trained only on the syntactic argument of the explicit statement of problem-/solution-hood), our classifiers should in principle be in a good position to generalise, i.e., find implicit statements too. In future work, we will measure to which degree this is the case. To facilitate further research on this topic, all code and data used in our experiments can be found here: www.cl.cam.ac.uk/~kh562/identifying-problems-and-solutions.html AcknowledgementsThe first author has been supported by an EPSRC studentship (Award Ref: 1641528). We thank the reviewers for their helpful comments. 1 http://acl-arc.comp.nus.edu.sg/ . 2 The corpus comprises 3,391,198 sentences, 71,149,169 words and 451,996,332 characters. 3 The head POS tags were found using a modification of the Collins’ Head Finder. This modified algorithm addresses some of the limitations of the head finding heuristics described by Collins ( 2003 ) and can be found here: http://nlp.stanford.edu/nlp/javadoc/javanlp/edu/stanford/nlp/trees/ModCollinsHeadFinder.html . 4 https://www.uni-hildesheim.de/ruppenhofer/data/modalia_release1.0.tgz. Contributor InformationKevin Heffernan, Email: [email protected] . Simone Teufel, Email: [email protected] . - Baccianella S, Esuli A, Sebastiani F. Sentiwordnet 3.0: An enhanced lexical resource for sentiment analysis and opinion mining. LREC. 2010; 10 :2200–2204. [ Google Scholar ]
- Becker, M., Palmer, A., & Frank, A. (2016). Clause types and modality in argumentative microtexts. In Workshop on foundations of the language of argumentation (in conjunction with COMMA) .
- Briscoe, T., Carroll, J., & Watson, R. (2006). The second release of the rasp system. In Proceedings of the COLING/ACL on interactive presentation sessions, association for computational linguistics pp. 77–80.
- Chandrasekaran B. Towards a taxonomy of problem solving types. AI Magazine. 1983; 4 (1):9. [ Google Scholar ]
- Charles M. Adverbials of result: Phraseology and functions in the problem-solution pattern. Journal of English for Academic Purposes. 2011; 10 (1):47–60. doi: 10.1016/j.jeap.2011.01.002. [ CrossRef ] [ Google Scholar ]
- Chen, D., Dyer, C., Cohen, S. B., & Smith, N. A. (2011). Unsupervised bilingual pos tagging with markov random fields. In Proceedings of the first workshop on unsupervised learning in NLP, association for computational linguistics pp. 64–71.
- Collins M. Head-driven statistical models for natural language parsing. Computational Linguistics. 2003; 29 (4):589–637. doi: 10.1162/089120103322753356. [ CrossRef ] [ Google Scholar ]
- Councill, I. G., Giles, C. L., & Kan, M. Y. (2008). Parscit: An open-source CRF reference string parsing package. In LREC .
- Curran, J. R., Clark, S., & Bos, J. (2007). Linguistically motivated large-scale NLP with C&C and boxer. In Proceedings of the 45th annual meeting of the ACL on interactive poster and demonstration sessions, association for computational linguistics pp. 33–36.
- Flowerdew L. Corpus-based analyses of the problem-solution pattern: A phraseological approach. Amsterdam: John Benjamins Publishing; 2008. [ Google Scholar ]
- Grimes JE. The thread of discourse. Berlin: Walter de Gruyter; 1975. [ Google Scholar ]
- Hall M, Frank E, Holmes G, Pfahringer B, Reutemann P, Witten IH. The weka data mining software: An update. ACM SIGKDD Explorations Newsletter. 2009; 11 (1):10–18. doi: 10.1145/1656274.1656278. [ CrossRef ] [ Google Scholar ]
- Hoey M. Textual interaction: An introduction to written discourse analysis. Portland: Psychology Press; 2001. [ Google Scholar ]
- Hutchins J. On the structure of scientific texts. UEA Papers in Linguistics. 1977; 5 (3):18–39. [ Google Scholar ]
- Jonassen DH. Toward a design theory of problem solving. Educational Technology Research and Development. 2000; 48 (4):63–85. doi: 10.1007/BF02300500. [ CrossRef ] [ Google Scholar ]
- Jordan MP. Short texts to explain problem-solution structures-and vice versa. Instructional Science. 1980; 9 (3):221–252. doi: 10.1007/BF00177328. [ CrossRef ] [ Google Scholar ]
- Kratzer, A. (1991). Modality. In von Stechow & Wunderlich (Eds.), Semantics: An international handbook of contemporary research .
- Le QV, Mikolov T. Distributed representations of sentences and documents. ICML. 2014; 14 :1188–1196. [ Google Scholar ]
- Lesk, M. (1986). Automatic sense disambiguation using machine readable dictionaries: How to tell a pine cone from an ice cream cone. In Proceedings of the 5th annual international conference on Systems documentation, ACM (pp. 24–26).
- Madnani, N., Tetreault, J., & Chodorow, M. (2012). Exploring grammatical error correction with not-so-crummy machine translation. In Proceedings of the seventh workshop on building educational applications using NLP, association for computational linguistics pp. 44–53.
- Mann WC, Thompson SA. Rhetorical structure theory: Toward a functional theory of text organization. Text-Interdisciplinary Journal for the Study of Discourse. 1988; 8 (3):243–281. doi: 10.1515/text.1.1988.8.3.243. [ CrossRef ] [ Google Scholar ]
- Marasović, A., & Frank, A. (2016). Multilingual modal sense classification using a convolutional neural network. In Proceedings of the 1st Workshop on Representation Learning for NLP .
- McKeown K, Daume H, Chaturvedi S, Paparrizos J, Thadani K, Barrio P, Biran O, Bothe S, Collins M, Fleischmann KR, et al. Predicting the impact of scientific concepts using full-text features. Journal of the Association for Information Science and Technology. 2016; 67 :2684–2696. doi: 10.1002/asi.23612. [ CrossRef ] [ Google Scholar ]
- Medlock B, Briscoe T. Weakly supervised learning for hedge classification in scientific literature. ACL, Citeseer. 2007; 2007 :992–999. [ Google Scholar ]
- Mikolov, T., Sutskever, I., Chen, K., Corrado, G. S., & Dean, J. (2013). Distributed representations of words and phrases and their compositionality. In Advances in neural information processing systems (pp. 3111–3119).
- Mohit, B., Schneider, N., Bhowmick, R., Oflazer, K., & Smith, N. A. (2012). Recall-oriented learning of named entities in arabic wikipedia. In Proceedings of the 13th conference of the European chapter of the association for computational linguistics, association for computational linguistics (pp. 162–173).
- Mullen T, Collier N. Sentiment analysis using support vector machines with diverse information sources. EMNLP. 2004; 4 :412–418. [ Google Scholar ]
- Nakov, P., Hearst, M. A. (2008). Solving relational similarity problems using the web as a corpus. In: ACL (pp. 452–460).
- Poon, H., & Domingos, P. (2009). Unsupervised semantic parsing. In Proceedings of the 2009 conference on empirical methods in natural language processing: Volume 1-association for computational linguistics (pp. 1–10).
- Ruppenhofer, J., & Rehbein, I. (2012). Yes we can!? Annotating the senses of English modal verbs. In Proceedings of the 8th international conference on language resources and evaluation (LREC), Citeseer (pp. 24–26).
- Saha, S. K., Mitra, P., & Sarkar, S. (2008). Word clustering and word selection based feature reduction for maxent based hindi ner. In ACL (pp. 488–495).
- Scott, M. (2001). Mapping key words to problem and solution. In Patterns of text: In honour of Michael Hoey Benjamins, Amsterdam (pp. 109–127).
- Siegel S. Nonparametric statistics for the behavioral sciences. New York: McGraw-hill; 1956. [ Google Scholar ]
- Strübing, J. (2007). Research as pragmatic problem-solving: The pragmatist roots of empirically-grounded theorizing. In The Sage handbook of grounded theory (pp. 580–602).
- Teufel, S., et al. (2000). Argumentative zoning: Information extraction from scientific text. PhD Thesis, Citeseer .
- Turney, P. D. (2002). Thumbs up or thumbs down?: Semantic orientation applied to unsupervised classification of reviews. In Proceedings of the 40th annual meeting on association for computational linguistics, association for computational linguistics (pp. 417–424).
- Van Dijk TA. Text and context explorations in the semantics and pragmatics of discourse. London: Longman; 1980. [ Google Scholar ]
- Wiebe J, Wilson T, Cardie C. Annotating expressions of opinions and emotions in language. Language Resources and Evaluation. 2005; 39 (2):165–210. doi: 10.1007/s10579-005-7880-9. [ CrossRef ] [ Google Scholar ]
- Wilson, T., Wiebe, J., & Hoffmann, P. (2005). Recognizing contextual polarity in phrase-level sentiment analysis. In Proceedings of the conference on human language technology and empirical methods in natural language processing, association for computational linguistics (pp. 347–354).
- Winter, E. O. (1968). Some aspects of cohesion. In Sentence and clause in scientific English . University College London.
- Zhou, M., Frank, A., Friedrich, A., & Palmer, A. (2015). Semantically enriched models for modal sense classification. In Workshop on linking models of lexical, sentential and discourse-level semantics (LSDSem) (p. 44).
 What Are Problem-Solving Skills? Definition and Examples - Share on Twitter Share on Twitter
- Share on Facebook Share on Facebook
- Share on LinkedIn Share on LinkedIn
 Forage puts students first. Our blog articles are written independently by our editorial team. They have not been paid for or sponsored by our partners. See our full editorial guidelines . Why do employers hire employees? To help them solve problems. Whether you’re a financial analyst deciding where to invest your firm’s money, or a marketer trying to figure out which channel to direct your efforts, companies hire people to help them find solutions. Problem-solving is an essential and marketable soft skill in the workplace. So, how can you improve your problem-solving and show employers you have this valuable skill? In this guide, we’ll cover: Problem-Solving Skills DefinitionWhy are problem-solving skills important, problem-solving skills examples, how to include problem-solving skills in a job application, how to improve problem-solving skills, problem-solving: the bottom line. Problem-solving skills are the ability to identify problems, brainstorm and analyze answers, and implement the best solutions. An employee with good problem-solving skills is both a self-starter and a collaborative teammate; they are proactive in understanding the root of a problem and work with others to consider a wide range of solutions before deciding how to move forward. Examples of using problem-solving skills in the workplace include: - Researching patterns to understand why revenue decreased last quarter
- Experimenting with a new marketing channel to increase website sign-ups
- Brainstorming content types to share with potential customers
- Testing calls to action to see which ones drive the most product sales
- Implementing a new workflow to automate a team process and increase productivity
Problem-solving skills are the most sought-after soft skill of 2022. In fact, 86% of employers look for problem-solving skills on student resumes, according to the National Association of Colleges and Employers Job Outlook 2022 survey . It’s unsurprising why employers are looking for this skill: companies will always need people to help them find solutions to their problems. Someone proactive and successful at problem-solving is valuable to any team. “Employers are looking for employees who can make decisions independently, especially with the prevalence of remote/hybrid work and the need to communicate asynchronously,” Eric Mochnacz, senior HR consultant at Red Clover, says. “Employers want to see individuals who can make well-informed decisions that mitigate risk, and they can do so without suffering from analysis paralysis.” Showcase new skillsBuild the confidence and practical skills that employers are looking for with Forage’s free job simulations. Problem-solving includes three main parts: identifying the problem, analyzing possible solutions, and deciding on the best course of action. >>MORE: Discover the right career for you based on your skills with a career aptitude test . Research is the first step of problem-solving because it helps you understand the context of a problem. Researching a problem enables you to learn why the problem is happening. For example, is revenue down because of a new sales tactic? Or because of seasonality? Is there a problem with who the sales team is reaching out to? Research broadens your scope to all possible reasons why the problem could be happening. Then once you figure it out, it helps you narrow your scope to start solving it. Analysis is the next step of problem-solving. Now that you’ve identified the problem, analytical skills help you look at what potential solutions there might be. “The goal of analysis isn’t to solve a problem, actually — it’s to better understand it because that’s where the real solution will be found,” Gretchen Skalka, owner of Career Insights Consulting, says. “Looking at a problem through the lens of impartiality is the only way to get a true understanding of it from all angles.” Decision-MakingOnce you’ve figured out where the problem is coming from and what solutions are, it’s time to decide on the best way to go forth. Decision-making skills help you determine what resources are available, what a feasible action plan entails, and what solution is likely to lead to success. On a ResumeEmployers looking for problem-solving skills might include the word “problem-solving” or other synonyms like “ critical thinking ” or “analytical skills” in the job description. “I would add ‘buzzwords’ you can find from the job descriptions or LinkedIn endorsements section to filter into your resume to comply with the ATS,” Matthew Warzel, CPRW resume writer, advises. Warzel recommends including these skills on your resume but warns to “leave the soft skills as adjectives in the summary section. That is the only place soft skills should be mentioned.” On the other hand, you can list hard skills separately in a skills section on your resume .  Forage Resume Writing MasterclassLearn how to showcase your skills and craft an award-winning resume with this free masterclass from Forage. Avg. Time: 5 to 6 hours Skills you’ll build: Resume writing, professional brand, professional summary, narrative, transferable skills, industry keywords, illustrating your impact, standing out In a Cover Letter or an InterviewExplaining your problem-solving skills in an interview can seem daunting. You’re required to expand on your process — how you identified a problem, analyzed potential solutions, and made a choice. As long as you can explain your approach, it’s okay if that solution didn’t come from a professional work experience. “Young professionals shortchange themselves by thinking only paid-for solutions matter to employers,” Skalka says. “People at the genesis of their careers don’t have a wealth of professional experience to pull from, but they do have relevant experience to share.” Aaron Case, career counselor and CPRW at Resume Genius, agrees and encourages early professionals to share this skill. “If you don’t have any relevant work experience yet, you can still highlight your problem-solving skills in your cover letter,” he says. “Just showcase examples of problems you solved while completing your degree, working at internships, or volunteering. You can even pull examples from completely unrelated part-time jobs, as long as you make it clear how your problem-solving ability transfers to your new line of work.” Learn How to Identify ProblemsProblem-solving doesn’t just require finding solutions to problems that are already there. It’s also about being proactive when something isn’t working as you hoped it would. Practice questioning and getting curious about processes and activities in your everyday life. What could you improve? What would you do if you had more resources for this process? If you had fewer? Challenge yourself to challenge the world around you. Think Digitally“Employers in the modern workplace value digital problem-solving skills, like being able to find a technology solution to a traditional issue,” Case says. “For example, when I first started working as a marketing writer, my department didn’t have the budget to hire a professional voice actor for marketing video voiceovers. But I found a perfect solution to the problem with an AI voiceover service that cost a fraction of the price of an actor.” Being comfortable with new technology — even ones you haven’t used before — is a valuable skill in an increasingly hybrid and remote world. Don’t be afraid to research new and innovative technologies to help automate processes or find a more efficient technological solution. CollaborateProblem-solving isn’t done in a silo, and it shouldn’t be. Use your collaboration skills to gather multiple perspectives, help eliminate bias, and listen to alternative solutions. Ask others where they think the problem is coming from and what solutions would help them with your workflow. From there, try to compromise on a solution that can benefit everyone. If we’ve learned anything from the past few years, it’s that the world of work is constantly changing — which means it’s crucial to know how to adapt . Be comfortable narrowing down a solution, then changing your direction when a colleague provides a new piece of information. Challenge yourself to get out of your comfort zone, whether with your personal routine or trying a new system at work. Put Yourself in the Middle of Tough MomentsJust like adapting requires you to challenge your routine and tradition, good problem-solving requires you to put yourself in challenging situations — especially ones where you don’t have relevant experience or expertise to find a solution. Because you won’t know how to tackle the problem, you’ll learn new problem-solving skills and how to navigate new challenges. Ask your manager or a peer if you can help them work on a complicated problem, and be proactive about asking them questions along the way. Career Aptitude TestWhat careers are right for you based on your skills? Take this quiz to find out. It’s completely free — you’ll just need to sign up to get your results! Step 1 of 3 Companies always need people to help them find solutions — especially proactive employees who have practical analytical skills and can collaborate to decide the best way to move forward. Whether or not you have experience solving problems in a professional workplace, illustrate your problem-solving skills by describing your research, analysis, and decision-making process — and make it clear that you’re the solution to the employer’s current problems. Looking to learn more workplace professional skills? Check out Two Sigma’s Professional Skills Development Virtual Experience Program . Image Credit: Christina Morillo / Pexels  Related Posts6 negotiation skills to level up your work life, how to build conflict resolution skills: case studies and examples, what is github uses and getting started, upskill with forage.  Build career skills recruiters are looking for. Mathematicians Are Edging Close to Solving One of the World's 7 Hardest Math ProblemsAnd there’s $1 million at stake.  - In new research, mathematicians have narrowed down one of the biggest outstanding problems in math.
- Huge breakthroughs in math and science are usually the work of many people over many years.
- Seven math problems were given a $1 million bounty each in 2000, and just one has been solved so far.
The “Millennium Problems” are seven infamously intractable math problems laid out in the year 2000 by the prestigious Clay Institute, each with $1 million attached as payment for a solution. They span all areas of math , as the Clay Institute was founded in 1998 to push the entire field forward with financial support for researchers and important breakthroughs. But the only solved Millennium Problem so far, the Poincare conjecture, illustrates one of the funny pitfalls inherent to offering a large cash prize for math. The winner, Grigori Perelman, refused the Clay prize as well as the prestigious Fields Medal. He withdrew from mathematics and public life in 2006, and even in 2010, he still insisted his contribution was the same as the mathematician whose work laid the foundation on which he built his proof, Richard Hamilton. Math, all sciences, and arguably all human inquiries are filled with pairs or groups that circle the same finding at the same time until one officially makes the breakthrough. Think about Sir Isaac Newton and Gottfried Leibniz, whose back-and-forth about calculus led to the combined version of the field we still study today. Rosalind Franklin is now mentioned in the same breath as her fellow discoverers of DNA, James Watson and Francis Crick. Even the Bechdel Test for women in media is sometimes called the Bechdel-Wallace Test, because humans are almost always in collaboration. That’s what makes this new paper so important. Two mathematicians—Larry Guth of the Massachusetts Institute of Technology (MIT) and James Maynard of the University of Oxford—collaborated on the new finding about how certain polynomials are formed and how they reach out into the number line. Maynard is just 37, and won the Fields Medal himself in 2022. Guth, a decade older, has won a number of important prizes with a little less name recognition. The Riemann hypothesis is not directly related to prime numbers , but it has implications that ripple through number theory in different ways (including with prime numbers). Basically, it deals with where and how the graph of a certain function of complex numbers crosses back and forth across axes. The points where the function crosses an axis is called a “zero,” and the frequency with which those zeroes appear is called the zero density. In the far reaches of the number line, prime numbers become less and less predictable (in the proverbial sense). They are not, so far, predictable in the literal sense—a fact that is an underpinning of modern encryption , where data is protected by enormous strings of integers made by multiplying enormous prime numbers together. The idea of a periodic table of primes, of any kind of template that could help mathematicians better understand where and how large primes cluster together or not, is a holy grail. In the new paper, Maynard and Guth focus on a new limitation of Dirichlet polynomials. These are special series of complex numbers that many believe are of the same type as the function involved in the Riemann hypothesis involves. In the paper, they claim they’ve proven that these polynomials have a certain number of large values, or solutions , within a tighter range than before. In other words, if we knew there might be an estimated three Dirichlet values between 50 and 100 before, now we may know that range to be between 60 and 90 instead. The eye exam just switched a blurry plate for a slightly less blurry one, but we still haven’t found the perfect prescription. “If one knows some more structure about the set of large values of a Dirichlet polynomial, then one can hope to have improved bound,” Maynard and Guth conclude. No, this is not a final proof of the Riemann hypothesis. But no one is suggesting it is. In advanced math, narrowing things down is also vital. Indeed, even finding out that a promising idea turns out to be wrong can have a lot of value—as it has a number of times in the related Twin Primes Conjecture that still eludes mathematicians. In a collaboration that has lasted 160 years and counting, mathematicians continue to take each step together and then, hopefully, compare notes.  Caroline Delbert is a writer, avid reader, and contributing editor at Pop Mech. She's also an enthusiast of just about everything. Her favorite topics include nuclear energy, cosmology, math of everyday things, and the philosophy of it all.  .css-cuqpxl:before{padding-right:0.3125rem;content:'//';display:inline;} Math .css-xtujxj:before{padding-left:0.3125rem;content:'//';display:inline;} Billiards With Memory Creates Intricate Patterns  A Wonder Clock Has Rocked the Scientific World  Machines About to Tackle Fermat’s Last Theorem  Can AI Help Solve Math’s Thorniest Mysteries?  The History of Pi  Experts Discovered the Secret Geometry of Life  Scientists Solved a 141-Year-Old Problem  The Perfect Table Size for Your Jigsaw Puzzle  Breaking the 1880s Silk Dress Cryptogram  10 of the Hardest Math Problems Ever Solved  Solution to Riddle of the Week #12: Licking Frogs - Skip to primary navigation
- Skip to main content
- Skip to primary sidebar
- Skip to footer
 Understanding ScienceHow science REALLY works... - Understanding Science 101
- Misconceptions
- The scientific community is global and diverse.
- The diversity of the scientific community helps facilitate specialization and provides different points of view that lead to diverse investigations, invigorate problem solving, and balance biases.
Misconception: Science is only done by “old, white men.” Correction: People from all over the world from many different backgrounds make up the scientific community. Read more about it. The scientific community: Diversity makes the differencePeople from all over the world from all sorts of different cultures and backgrounds are a part of the scientific community, and science benefits from these different perspectives and contributions. At many points in history, Western science has been the exclusive domain of white men, but that is changing … slowly. For example, since people who identify as women represent about 50% of the U.S. population, they should make up 50% of scientists, too; over the past 30 years, women have come to hold a larger share of jobs in the life and physical sciences in the U.S. – though not half yet. And while Hispanic and Black people make up a significant percentage of the life and physical science workforce in the U.S. today, they still face barriers that lead to underrepresentation and are paid less than white and Asian workers. 1 Many people are working on a variety of fronts to expand access and stamp out exclusion, but there is a long way still to go. 2 You can learn more about some of the barriers that people of color, women, and others face within science here . Of course, “diversity” includes much more than just racial and gender identity – and the scientific enterprise benefits from participants with different cultures, religions, ages, sexual orientations, gender identities, disabilities, incarceration histories, classes, and so much more. Here are just a few of the ways that science benefits from diverse participants: Diverse scientists ask diverse questionsWhile science can investigate any part of the natural world, progress is only made on those questions that scientists think to ask. Our backgrounds and identities shape the questions we ask about the world. For example, Black scientists are more likely to study health disparities than are white scientists, and female scientists are more likely to study pregnancy and education than are male scientists. 3 If we want science to address the whole natural world and problems that affect all sorts of people, then we need all sorts of people to be able to participate in science. Diversity facilitates specializationScientists have different strengths and different interests. People from different backgrounds may approach the same question in different ways. So, the biologist with a penchant for math, the biologist with an interest in human behavior, and the biologist who can’t get enough of microscopes and lab work can all focus on their strengths. While each might choose to tackle the same topic (say, human cognition), they will do so from different angles, contributing to a more complete understanding of the topic. Diversity invigorates problem solvingScience benefits greatly from a community that approaches problems in a variety of creative ways. A diverse community is better able to generate new research methods, explanations, and ideas, which can help science over challenging hurdles and shed new light on problems. For example, scientists who study how science works (yes, that’s a thing!) have found that scholars from historically excluded backgrounds (e.g., African-American PhD students) produce more innovative research than their counterparts from overrepresented backgrounds. 4 Similarly, because of their identities and backgrounds, Indigenous scientists often see ecological challenges in different terms than scientists from dominant backgrounds; in particular, they may be more likely to take a holistic approach, integrating many subdisciplines of biology and recognizing the interconnected nature of an environmental problem. 5 Indigenous scientists also have access to valuable traditional knowledge built from generations of experience with and connections to a particular place, such as recognizing differences in subspecies that non-indigenous scientists might not. 6 Diverse perspectives simply lead to richer and more exciting scientific discoveries. NEURODIVERSE IDEASScientist Temple Grandin studies animal behavior. She is well known for investigating how animals raised as livestock react to their surroundings and for developing ways to make our treatment of livestock more humane. Grandin is autistic and has explained in interviews and talks how this has deeply shaped her science. For example, she describes her own thinking as based in pictures, not words, and credits that aspect of her autism with helping her relate to livestock animals and focus on their visual perception. 7 This was an important part of her early research, which showed how small visual elements in a slaughterhouse, like shadows, can cause stress for livestock. Grandin’s autism led to research and compassionate innovations in the livestock industry that might not have come about otherwise. Diversity balances biasesScience benefits from practitioners with diverse beliefs, backgrounds, and values to balance out the biases that would occur if science were practiced by a narrow subset of humanity. As an example, consider the ongoing scientific investigation of climate change. With such a hot-button issue, personal beliefs about the environment, the economy, business, and politics could unwittingly bias one’s search for or assessment of the evidence. But science relies on a diverse community, whose personal views run the gamut: liberal to conservative, tree-hugging to business-friendly, and all sorts of combinations thereof. Scientists strive to be impartial and objective in their assessments of scientific issues, but when personal biases sneak in (and they are bound to – scientists are, after all, human!), a diverse scientific community can help keep them in check. We should do all we can to support more different sorts of people becoming scientists, not only because everyone deserves to be able to pursue their curiosity and experience the joy of science, but also because we all stand to benefit from science informed and pushed forward by diverse perspectives. If scientists were all the same, scientific controversy might be rare, but we would learn less about a much smaller portion of the natural world. Science depends on diversity – and yet, science has been, and very often still is, exclusionary. Many people are beginning to recognize this and are taking steps on a variety of fronts to make science more inclusive – from training to hiring, from workplace culture to funding systems. There is a long road to travel before science will reflect the diverse societies in which it is embedded and serve the whole spectrum of the world’s inhabitants. For an example of how diverse participants can help advance scientific knowledge, check out the story of Lynn Margulis, Cells within cells: An extraordinary claim with extraordinary evidence . - Learn more about science as a global human endeavor. Take a whirlwind tour of Science around the world .
- View this short video addressing the needs and benefits of diversity in science.
1 Pew Research Center, April, 2021, “STEM Jobs See Uneven Progress in Increasing Gender, Racial and Ethnic Diversity.” 2 Tilghman, S., Alberts, B., Colón-Ramos, D., Dzirasa, K., Kimble, J., and Varmus, H. (2021). Concrete steps to diversity the scientific workforce. Science. 372: 133-135. 3 Hoppe, T. A., Litovitz, A., Willis, K. A., Meseroll, R. A., Perkins, M. J., Hutchings, B. I.,… and Santangelo, G. M. (2019). Topic choice contributes to the lower rate of NIH awards to African-American/black scientists. Science Advances. DOI 10.2226/sciadv.aaw7238 Kozlowski, D., Larivière, V., Sugimoto, C. R., and Monroe-White, T. (2022). Intersectional inequalities in science. Proceedings of the National Academy of Sciences USA . 119: e2113067119. 4 Hofstra, B., Kulkarni, V. V., Munoz-Najar Galvez, S., and McFarland, D. A. The diversity-innovation paradox in Science. (2020). Proceedings of the National Academy of Sciences USA . 117: 9284-9291. 5 Hernandez, J. (2022). Fresh Banana Leaves: Healing Indigenous Landscapes Through Indigenous Science. North Atlantic Books. 6 For example, see Stronen, A. V., Navid, E. L., Quinn, M. S., Paquet, P. C., Bryan, H. M., and Darimont, C. T. (2014). Population genetic structure of gray wolves ( Canis lupus ) in a marine archipelago suggests island-mainland differentiation consistent with dietary niche. BMC Ecology. 14: 1-9. For more on the potential future relationship between traditional and western scientific knowledge, see Reid, A. J., Eckert, L. E., Lane, J., Young, N., Hinch, S. G., Darimont, S. J. C., … and Marshall, A. (2020). “Two-eyed seeing”: an indigenous framework to transform fisheries research and management. Fish and Fisheries . https://doi.org/10.1111/faf.12516 7 Richter, R. (2014). 5 Question: Temple Grandin discusses autism, animal communication. Stanford Medicine News Center. https://med.stanford.edu/news/all-news/2014/11/5-questions--temple-grandin-discusses-autism--animal-communicati.html The social side of science: A human and community endeavor Science: A community enterprise Subscribe to our newsletter - The science flowchart
- Science stories
- Grade-level teaching guides
- Teaching resource database
- Journaling tool
- Data Science
- Trending Now
- Data Structures
- System Design
- Foundational Courses
- Practice Problem
- Machine Learning
- Data Science Using Python
- Web Development
- Web Browser
- Design Patterns
- Software Development
- Product Management
- Programming
Welcome to the daily solving of our PROBLEM OF THE DAY with Jay Dalsaniya We will discuss the entire problem step-by-step and work towards developing an optimized solution. This will not only help you brush up on your concepts of Tree but also build up problem-solving skills. Given a binary tree and an integer target , check whether there is a root-to-leaf path with its sum as target . Input: tree = 1, target = 2 / \ 2 3 Output: false Explanation: There is no root to leaf path with sum 2. Give the problem a try before going through the video. All the best!!! Problem Link: https://practice.geeksforgeeks.org/problems/root-to-leaf-path-sum/1  InformationInitiativesYou are accessing a machine-readable page. In order to be human-readable, please install an RSS reader. All articles published by MDPI are made immediately available worldwide under an open access license. No special permission is required to reuse all or part of the article published by MDPI, including figures and tables. For articles published under an open access Creative Common CC BY license, any part of the article may be reused without permission provided that the original article is clearly cited. For more information, please refer to https://www.mdpi.com/openaccess . Feature papers represent the most advanced research with significant potential for high impact in the field. A Feature Paper should be a substantial original Article that involves several techniques or approaches, provides an outlook for future research directions and describes possible research applications. Feature papers are submitted upon individual invitation or recommendation by the scientific editors and must receive positive feedback from the reviewers. Editor’s Choice articles are based on recommendations by the scientific editors of MDPI journals from around the world. Editors select a small number of articles recently published in the journal that they believe will be particularly interesting to readers, or important in the respective research area. The aim is to provide a snapshot of some of the most exciting work published in the various research areas of the journal. Original Submission Date Received: . - Active Journals
- Find a Journal
- Proceedings Series
- For Authors
- For Reviewers
- For Editors
- For Librarians
- For Publishers
- For Societies
- For Conference Organizers
- Open Access Policy
- Institutional Open Access Program
- Special Issues Guidelines
- Editorial Process
- Research and Publication Ethics
- Article Processing Charges
- Testimonials
- Preprints.org
- SciProfiles
- Encyclopedia
 Article Menu - Subscribe SciFeed
- Recommended Articles
- Author Biographies
- Google Scholar
- on Google Scholar
- Table of Contents
Find support for a specific problem in the support section of our website. Please let us know what you think of our products and services. Visit our dedicated information section to learn more about MDPI. JSmol ViewerThe use of socioscientific issues in science lessons: a scoping review.  1. Introduction2. linking socioscientific issues with a scientific literate citizenry, 3.1. identifying the research questions, 3.2. identifying relevant studies, 3.3. selection of studies for inclusion in this review, 4.1. rq1: studies identified in the scopus and web of science databases, 4.2. rq2: most cited articles and most frequent authors, 4.3. rq3: geographical distribution of authors, 4.4. rq4: journals with the highest number of publications, 4.5. rq5: topics of socioscientific issues and subjects in which they are taught, 4.6. rq6: units of analysis and academic contexts, 4.6.1. units of analysis, 4.6.2. academic contexts, 4.7. rq7: methodological approaches, 4.8. rq8: teaching and learning models, 4.8.1. socioscientific inquiry-based learning, 4.8.2. problem-based, context-based, and case-based learning, 4.8.3. model-based learning, 4.9. rq9: resources used in teaching and learning processes, 4.9.1. press articles, 4.9.2. digital resources for data mapping and visualization, 4.10. rq10: forms of action and expression in teaching and learning processes, 4.10.1. debate, discussion techniques, deliberative democracy, negotiation, 4.10.2. drama and role-playing, 4.10.3. drawing, 4.11. rq11: challenges identified, 4.11.1. challenges at the level of teaching practice, 4.11.2. challenges at the level of teacher training, 4.11.3. challenges at the student level, 4.11.4. challenges at the curriculum level. As we move from the past and present to the future, responsibility takes on yet another form. We are no longer engaged with making sense of things that have already been done. Nor are we dealing with pressing issues that need a prompt reaction. On the contrary, we are engaged in activities that are generative of possible futures. In other words, we adopt an attitude that is forward-looking. This means that we are called to exploring possibilities as they unfold without firm ground or the guarantee that what we are doing is the right thing. (p. 8) 5. Discussion of Results6. conclusions. Cold-type SSI education is a fairly traditional science education with some socio-contextualization. It is characterized by monodisciplinarity and a focus on content learning. Hot-type SSIs, on the other hand, also emphasize transdisciplinarity and political citizenship. (p. 21) Author ContributionsInstitutional review board statement, data availability statement, conflicts of interest. - Díaz Moreno, N.; Jiménez Liso, M.R. Las controversias sociocientíficas: Temáticas e importancia para la educación científica. Rev. Eureka Sobre Enseñ. Divulg. Las Cienc. 2012 , 9 , 54–70. [ Google Scholar ] [ CrossRef ]
- Romero-Ariza, M.; Abril, A.M.; Quesada, A. Design and Evaluation of Teaching Materials for Responsible Research and Innovation. Sisyphus J. Educ. 2017 , 5 , 28–43. [ Google Scholar ]
- Archila, P.A.; Truscott de Mejía, A.-M.; Restrepo, S. Using Drama to Enrich Students’ Argumentation About Genetically Modified Foods. Sci. Educ. 2023 , 32 , 635–668. [ Google Scholar ] [ CrossRef ]
- Nida, S.; Marsuki, M.F.; Eilks, I. Palm-Oil-Based Biodiesel in Indonesia: A Case Study on a Socioscientific Issue That Engages Students to Learn Chemistry and Its Impact on Society. J. Chem. Educ. 2021 , 98 , 2536–2548. [ Google Scholar ] [ CrossRef ]
- Cebrián-Robles, D.; España-Ramos, E.; Reis, P. Introducing Preservice Primary Teachers to Socioscientific Activism through the Analysis and Discussion of Videos. Int. J. Sci. Educ. 2021 , 43 , 2457–2478. [ Google Scholar ] [ CrossRef ]
- Alcaraz-Dominguez, S.; Barajas, M. Conceiving Socioscientific Issues in Stem Lessons from Science Education Research and Practice. Educ. Sci. 2021 , 11 , 238. [ Google Scholar ] [ CrossRef ]
- Perales, F.; Aróstegui, J.L. The STEAM Approach: Implementation and Educational, Social and Economic Consequences. Arts Educ. Policy Rev. 2021 , 125 , 59–67. [ Google Scholar ] [ CrossRef ]
- Liao, C. From Interdisciplinary to Transdisciplinary: An Arts-Integrated Approach to STEAM Education. Art Educ. 2016 , 69 , 44–49. [ Google Scholar ] [ CrossRef ]
- Hodson, D. Going Beyond STS Education: Building a Curriculum for Sociopolitical Activism. Can. J. Sci. Math. Technol. Educ. 2020 , 20 , 592–622. [ Google Scholar ] [ CrossRef ]
- Sakschewski, M.; Eggert, S.; Schneider, S.; Bögeholz, S. Students’ Socioscientific Reasoning and Decision-Making on Energy-Related Issues-Development of a Measurement Instrument. Int. J. Sci. Educ. 2014 , 36 , 2291–2313. [ Google Scholar ] [ CrossRef ]
- Hodson, D. Time for Action: Science Education for an Alternative Future. Int. J. Sci. Educ. 2003 , 25 , 645–670. [ Google Scholar ] [ CrossRef ]
- Reiss, M.J.; Millar, R.; Osborne, J. Beyond 2000: Science/Biology Education for the Future. J. Biol. Educ. 1999 , 33 , 68. [ Google Scholar ] [ CrossRef ]
- United Nations Development Programme. Sustainable Development Goals. Available online: https://www.undp.org/sustainable-development-goals (accessed on 8 June 2024).
- Chowdhury, T.B.M.; Holbrook, J.; Rannikmäe, M. Addressing Sustainable Development: Promoting Active Informed Citizenry through Trans-Contextual Science Education. Sustainability 2020 , 12 , 3259. [ Google Scholar ] [ CrossRef ]
- Klaver, L.T.; Walma van der Molen, J.H. Measuring Pupils’ Attitudes Towards Socioscientific Issues: Development and Validation of a Questionnaire. Sci. Educ. 2021 , 30 , 317–344. [ Google Scholar ] [ CrossRef ]
- Zeidler, D.L.; Walker, K.A.; Ackett, W.A.; Simmons, M.L. Tangled up in Views: Beliefs in the Nature of Science and Responses to Socioscientific Dilemmas. Sci. Educ. 2002 , 86 , 343–367. [ Google Scholar ] [ CrossRef ]
- Zeidler, D.L. Socioscientific Issues as a Curriculum Emphasis: Theory, Research, and Practice. In Handbook of Research on Science Education, Volume II ; Routledge: London, UK, 2014; ISBN 978-0-203-09726-7. [ Google Scholar ]
- Sadler, T.D. Informal Reasoning Regarding Socioscientific Issues: A Critical Review of Research. J. Res. Sci. Teach. 2004 , 41 , 513–536. [ Google Scholar ] [ CrossRef ]
- Kim, G.; Ko, Y.; Lee, H. The Effects of Community-Based Socioscientific Issues Program (SSI-COMM) on Promoting Students’ Sense of Place and Character as Citizens. Int. J. Sci. Math. Educ. 2020 , 18 , 399–418. [ Google Scholar ] [ CrossRef ]
- Roth, W.-M.; Barton, A.C. Rethinking Scientific Literacy ; Routledge: New York, NY, USA, 2004; ISBN 978-0-203-46391-8. [ Google Scholar ]
- Bencze, L.; Sperling, E.; Carter, L. Students’ Research-Informed Socio-Scientific Activism: Re/Visions for a Sustainable Future. Res. Sci. Educ. 2012 , 42 , 129–148. [ Google Scholar ] [ CrossRef ]
- Mang, H.M.A.; Chu, H.-E.; Martin, S.N.; Kim, C.-J. An SSI-Based STEAM Approach to Developing Science Programs. Asia-Pac. Sci. Educ. 2021 , 9 , 1–37. [ Google Scholar ] [ CrossRef ]
- Roberts, D.A. Scientific Literacy/Science Literacy. In Handbook of Research on Science Education ; Routledge: London, UK, 2007; ISBN 978-0-203-82469-6. [ Google Scholar ]
- Sjöström, J.; Frerichs, N.; Zuin, V.G.; Eilks, I. Use of the Concept of Bildung in the International Science Education Literature, Its Potential, and Implications for Teaching and Learning. Stud. Sci. Educ. 2017 , 53 , 165–192. [ Google Scholar ] [ CrossRef ]
- Sjöström, J.; Eilks, I. Reconsidering Different Visions of Scientific Literacy and Science Education Based on the Concept of Bildung. In Cognition, Metacognition, and Culture in STEM Education: Learning, Teaching and Assessment ; Dori, Y.J., Mevarech, Z.R., Baker, D.R., Eds.; Springer International Publishing: Cham, Switzerland, 2018; pp. 65–88. ISBN 978-3-319-66659-4. [ Google Scholar ]
- Arksey, H.; O’Malley, L. Scoping Studies: Towards a Methodological Framework. Int. J. Soc. Res. Methodol. 2005 , 8 , 19–32. [ Google Scholar ] [ CrossRef ]
- Levac, D.; Colquhoun, H.; O’Brien, K.K. Scoping Studies: Advancing the Methodology. Implement. Sci. 2010 , 5 , 69. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- PRISMA. PRISMA 2020 Checklist. Available online: https://www.prisma-statement.org/prisma-2020-checklist (accessed on 8 June 2024).
- Lederman, N.; Antink, A.; Bartos, S. Nature of Science, Scientific Inquiry, and Socio-Scientific Issues Arising from Genetics: A Pathway to Developing a Scientifically Literate Citizenry. Sci. Educ. 2014 , 23 , 285–302. [ Google Scholar ] [ CrossRef ]
- Lee, H.; Yoo, J.; Choi, K.; Kim, S.-W.; Krajcik, J.; Herman, B.C.; Zeidler, D.L. Socioscientific Issues as a Vehicle for Promoting Character and Values for Global Citizens. Int. J. Sci. Educ. 2013 , 35 , 2079–2113. [ Google Scholar ] [ CrossRef ]
- Jordan, R.; Crall, A.; Gray, S.; Phillips, T.; Mellor, D. Citizen Science as a Distinct Field of Inquiry. BioScience 2015 , 65 , 208–211. [ Google Scholar ] [ CrossRef ]
- Chung, Y.; Yoo, J.; Kim, S.-W.; Lee, H.; Zeidler, D.L. Enhancing Students’ Communication Skills in the Science Classroom Through Socioscientific Issues. Int. J. Sci. Math. Educ. 2016 , 14 , 1–27. [ Google Scholar ] [ CrossRef ]
- Clausen, S.W. Exploring the Pedagogical Content Knowledge of Danish Geography Teachers: Teaching Weather Formation and Climate Change. Int. Res. Geogr. Environ. Educ. 2018 , 27 , 267–280. [ Google Scholar ] [ CrossRef ]
- Eggert, S.; Nitsch, A.; Boone, W.J.; Nückles, M.; Bögeholz, S. Supporting Students’ Learning and Socioscientific Reasoning About Climate Change—The Effect of Computer-Based Concept Mapping Scaffolds. Res. Sci. Educ. 2017 , 47 , 137–159. [ Google Scholar ] [ CrossRef ]
- Feucht, F.C.; Michaelson, K.; Hany, S.L.; Maziarz, L.N.; Ziegler, N.E. Is the Earth Crying Wolf? Exploring Knowledge Source and Certainty in High School Students’ Analysis of Global Warming News. Sustainability 2021 , 13 , 12899. [ Google Scholar ] [ CrossRef ]
- Gustafsson, B.; Öhman, J. DEQUAL: A Tool for Investigating Deliberative Qualities in Students’ Socioscientific Conversations. Int. J. Environ. Sci. Educ. 2013 , 8 , 319–338. [ Google Scholar ] [ CrossRef ]
- Ho, L.-C.; Seow, T. Disciplinary Boundaries and Climate Change Education: Teachers’ Conceptions of Climate Change Education in the Philippines and Singapore. Int. Res. Geogr. Environ. Educ. 2017 , 26 , 240–252. [ Google Scholar ] [ CrossRef ]
- Namdar, B.; Namdar, A.O. Role Reversal to Facilitate Social & Moral CompassionA Case for Climate Change as an Ethics Dilemma. Am. Biol. Teach. 2022 , 84 , 242–245. [ Google Scholar ] [ CrossRef ]
- Park, Y.-S. Exploring Secondary Earth Science Preservice Teachers’ Competency in Understanding Democratic Citizenship. J. Korean Earth Sci. Soc. 2023 , 44 , 342–358. [ Google Scholar ] [ CrossRef ]
- Walsh, E.M.; Tsurusaki, B.K. “Thank You for Being Republican”: Negotiating Science and Political Identities in Climate Change Learning. J. Learn. Sci. 2018 , 27 , 8–48. [ Google Scholar ] [ CrossRef ]
- Ariza, M.R.; Christodoulou, A.; van Harskamp, M.; Knippels, M.-C.P.J.; Kyza, E.A.; Levinson, R.; Agesilaou, A. Socio-scientific Inquiry-based Learning as a Means toward Environmental Citizenship. Sustainability 2021 , 13 , 11509. [ Google Scholar ] [ CrossRef ]
- Ginosar, A.; Tal, T. Teaching Journalistic Texts in Science Classes: The Importance of Media Literacy. J. Sci. Educ. Technol. 2018 , 27 , 205–214. [ Google Scholar ] [ CrossRef ]
- Kinslow, A.T.; Sadler, T.D.; Nguyen, H.T. Socio-Scientific Reasoning and Environmental Literacy in a Field-Based Ecology Class. Environ. Educ. Res. 2019 , 25 , 388–410. [ Google Scholar ] [ CrossRef ]
- Liu, S.; Hou, Q.; Guo, L. Based on Environmental Experience to Discuss the Effect of Environmental Education on Environmental Value. EKOLOJI 2018 , 27 , 991–997. [ Google Scholar ]
- Lebo, N.; Eames, C.; Coll, R.; Otrel-Cass, K. Toward Ecological Literacy: A Permaculture Approach to Junior Secondary Science. Aust. J. Environ. Educ. 2014 , 29 , 241–242. [ Google Scholar ] [ CrossRef ]
- McGregor, D.; Frodsham, S.; Deller, C. Participatory Inquiries That Promote Consideration of Socio-Scientific Issues Related to Sustainability within Three Different Contexts: Agriculture, Botany and Palaeontology. Sustainability 2023 , 15 , 6895. [ Google Scholar ] [ CrossRef ]
- Newton, M.H.; Zeidler, D.L. Developing Socioscientific Perspective Taking. Int. J. Sci. Educ. 2020 , 42 , 1302–1319. [ Google Scholar ] [ CrossRef ]
- Birmingham, D.; Calabrese Barton, A. Putting on a Green Carnival: Youth Taking Educated Action on Socioscientific Issues. J. Res. Sci. Teach. 2014 , 51 , 286–314. [ Google Scholar ] [ CrossRef ]
- Gulacar, O.; Marwaha, R.; Goradia, K.R. Examining Changes in Students’ Perception of Science Relevancy and Their Career Aspirations: Integrating Sustainability-Oriented Socio-Scientific Issues into General Chemistry Curriculum. Sustain. Chem. Pharm. 2022 , 25 , 100577. [ Google Scholar ] [ CrossRef ]
- Ramírez, J.S.A.; Chacón, Á.E.R. Teaching Physics by Addressing Socio-Scientific Issues in the Colombian Context. Góndola Enseñ. Aprendiz. Cienc. 2023 , 18 , 52–65. [ Google Scholar ] [ CrossRef ]
- Shasha-Sharf, H.; Tal, T. Energy Policy as a Socio-Scientific Issue: Argumentation in the Context of Economic, Environmental and Citizenship Education. Sustainability 2023 , 15 , 7647. [ Google Scholar ] [ CrossRef ]
- Cha, J.; Kim, H.; Kan, S.; Foo, W.; Low, X.; Ow, J.; Chandran, P.; Lee, G.; Yong, J.; Chia, P. Integrating Organic Chemical-Based Socio-Scientific Issues Comics into Chemistry Classroom: Expanding Chemists’ Toolbox. GREEN Chem. Lett. Rev. 2021 , 14 , 699–709. [ Google Scholar ] [ CrossRef ]
- Eilks, I. Science Education and Education for Sustainable Development—Justifications, Models, Practices and Perspectives. Eurasia J. Math. Sci. Technol. Educ. 2015 , 11 , 149–158. [ Google Scholar ] [ CrossRef ]
- Zoller, U. Research-Based Transformative Science/STEM/STES/STESEP Education for “Sustainability Thinking”: From Teaching to “Know” to Learning to “Think”. Sustainability 2015 , 7 , 4474–4491. [ Google Scholar ] [ CrossRef ]
- Fernández-Oliveras, A.; Martín-Gámez, C.; Díaz-Moreno, N.; Crujeiras-Pérez, B. Nuclear Cementery, Yes or No? A Proposal for Initial Teacher Training in Critical Thinking. Estud. Pedagógicos Valdivia 2022 , 48 , 11–31. [ Google Scholar ] [ CrossRef ]
- Lopez-Fernandez, M.; Gonzalez-Garcia, F.; Franco-Mariscal, A. How Can Socio-Scientific Issues Help Develop Critical Thinking in Chemistry Education? A Reflection on the Problem of Plastics. J. Chem. Educ. 2022 , 99 , 3435–3442. [ Google Scholar ] [ CrossRef ]
- Aivelo, T.; Uitto, A. Teachers’ Choice of Content and Consideration of Controversial and Sensitive Issues in Teaching of Secondary School Genetics. Int. J. Sci. Educ. 2019 , 41 , 2716–2735. [ Google Scholar ] [ CrossRef ]
- Cebesoy, U.; Oztekin, C. Genetics Literacy: Insights From Science Teachers’ Knowledge, Attitude, and Teaching Perceptions. Int. J. Sci. Math. Educ. 2018 , 16 , 1247–1268. [ Google Scholar ] [ CrossRef ]
- Domenech-Casal, J. Proposal of a Frame for Designing Didactic Activities on Socio-Scientific Issues. Study with Two Activities on Genetics. Rev. Eureka Sobre Enseñ. Divulg. Las Cienc. 2017 , 14 , 601–620. [ Google Scholar ] [ CrossRef ]
- Goldschmidt, M.; Scharfenberg, F.-J.; Bogner, F.X. Instructional Efficiency of Different Discussion Approaches in an Outreach Laboratory: Teacher-Guided versus Student-Centered. J. Educ. Res. 2016 , 109 , 27–36. [ Google Scholar ] [ CrossRef ]
- McKnight, L.; Pearce, A.; Willis, A.; Young, M.-A.; Terrill, B. Supporting Teachers to Use Genomics as a Context in the Classroom: An Evaluation of Learning Resources for High School Biology. J. Community Genet. 2021 , 12 , 653–662. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Mehltretter Drury, S.A.; Bost, A.G.; Wysocki, L.M.; Ingram, A.L. Encouraging Science Communication through Deliberative Pedagogy: A Study of a Gene Editing Deliberation in a Nonmajors Biology Course. J. Microbiol. Biol. Educ. 2019 , 19 . [ Google Scholar ] [ CrossRef ]
- Bayram-Jacobs, D.; Wieske, G.; Henze, I. A Chemistry Lesson for Citizenship: Students’ Use of Different Perspectives in Decision-Making about the Use and Sale of Laughing Gas. Educ. Sci. 2019 , 9 , 100. [ Google Scholar ] [ CrossRef ]
- Calvet, A.; Bargallo, C.; Tort, M.; Tallada, A. The Medicalization of Society as a Context for Promoting the Development and Use of Scientific Knowledge Related to the Human Body. Enseñanza Cienc. 2015 , 33 , 101–125. [ Google Scholar ] [ CrossRef ]
- Mnguni, L. An Investigation into the Curriculum Ideology That Foregrounds the Presentation of HIV/AIDS Content in Selected South Africa Life Sciences Textbooks. Int. J. STEM Educ. 2019 , 6 , 25. [ Google Scholar ] [ CrossRef ]
- Puig, B.; Blanco-Anaya, P.; Pérez-Maceira, J.J. “Fake News” or Real Science? Critical Thinking to Assess Information on COVID-19. Front. Educ. 2021 , 6 , 646909. [ Google Scholar ] [ CrossRef ]
- Senchina, D. Disease Outbreaks as Vehicles for Exploring “engaged Citizen” Themes through a Course on the History of Infectious Diseases. FEMS Microbiol. Lett. 2017 , 364 , fnw242. [ Google Scholar ] [ CrossRef ] [ PubMed ]
- Simonneaux, L.; Panissal, N.; Brossais, E. Students’ Perception of Risk About Nanotechnology After an SAQ Teaching Strategy. Int. J. Sci. Educ. 2013 , 35 , 2376–2406. [ Google Scholar ] [ CrossRef ]
- Gormally, C.; Heil, A. A Vision for University Biology Education for Non-Science Majors. CBE Life Sci. Educ. 2022 , 21 , es5. [ Google Scholar ] [ CrossRef ]
- Ladachart, L.; Ladachart, L. Preservice Biology Teachers’ Decision-Making and Informal Reasoning about Culture-Based Socioscientific Issues. Int. J. Sci. Educ. 2021 , 43 , 641–671. [ Google Scholar ] [ CrossRef ]
- Moreno, N.D. Portraying Socioscientific Issues in the Press. An Educational Tool for Scientific Literacy. Rev. Eureka Sobre Enseñ. Divulg. Las Cienc. 2019 , 16 , 1102. [ Google Scholar ] [ CrossRef ]
- Varis, K.; Jappinen, I.; Karkkainen, S.; Keinonen, T.; Vayrynen, E. Promoting Participation in Society through Science Education. Sustainability 2018 , 10 , 3412. [ Google Scholar ] [ CrossRef ]
- Avsar Erumit, B.; Yuksel, T. Developing and Using Physical Dynamic Models On Socioscientific Issues to Present Nature Of Science Ideas. Int. J. Sci. Math. Educ. 2023 , 21 , 1031–1056. [ Google Scholar ] [ CrossRef ]
- Palma-Jiménez, M.; Cebrián-Robles, D.; Blanco-López, Á. Impact of Instruction Based on a Validated Learning Progression on the Argumentation Competence of Preservice Elementary Science Teachers. Sci. Educ. 2023 . [ Google Scholar ] [ CrossRef ]
- Pitiporntapin, S.; Yutakom, N.; Sadler, T.D. Thai Pre-Service Science Teachers’ Struggles in Using Socio-Scientific Issues (SSIs) during Practicum. Asia-Pac. Forum Sci. Learn. Teach. 2016 , 17 . [ Google Scholar ]
- Rundgren, C.-J.; Chang Rundgren, S.-N. Aiming for Responsible and Competent Citizenship through Teacher Professional Development on Teaching Socioscientific Inquiry-Based Learning (SSIBL). Asia-Pac. Forum Sci. Learn. Teach. 2018 , 19 , 2. [ Google Scholar ]
- Salcedo-Armijo, E.; Cano-Iglesias, M.J.; Blanco-López, Á.; Franco-Mariscal, A.J. Uso de pruebas y decisiones de profesores en formación inicial en un debate sobre prohibición de plásticos. Educ. Quím. 2023 , 34 , 104–118. [ Google Scholar ] [ CrossRef ]
- van der Leij, T.; Avraamidou, L.; Wals, A.; Goedhart, M. Biology Students’ Morality When Engaged With Moral Dilemmas in the Human-Nature Context. Front. Educ. 2021 , 6 , 729685. [ Google Scholar ] [ CrossRef ]
- Georgiou, Y.; Kyza, E.A. Fostering Chemistry Students’ Scientific Literacy for Responsible Citizenship through Socio-Scientific Inquiry-Based Learning (SSIBL). Sustainability 2023 , 15 , 6442. [ Google Scholar ] [ CrossRef ]
- Lee, S.W.; Tran, S. Students Need More than Content Knowledge To Counter Vaccine Hesitancy. J. Microbiol. Biol. Educ. 2023 , 24 , e00047-23. [ Google Scholar ] [ CrossRef ]
- Alcaraz-Dominguez, S.; Barajas, M. Conceptualization of Socioscientific Issues in Educational Practice from a Review of Research in Science Education. Int. J. Inf. Educ. Technol. 2021 , 11 , 297–302. [ Google Scholar ] [ CrossRef ]
- Maass, K.; Sorge, S.; Romero-Ariza, M.; Hesse, A.; Straser, O. Promoting Active Citizenship in Mathematics and Science Teaching. Int. J. Sci. Math. Educ. 2022 , 20 , 727–746. [ Google Scholar ] [ CrossRef ]
- Chowdhury, T.; Holbrook, J.; Reis, P.; Rannikmäe, M. Bangladeshi Science Teachers’ Perceived Importance and Perceived Current Practices in Promoting Science Education Through a Context-Based, Socio-Scientific Framework. Sci. Educ. 2022 , 31 , 487–523. [ Google Scholar ] [ CrossRef ]
- Bardone, E.; Burget, M.; Pedaste, M. The RRI Map: Making Sense of Responsible Research and Innovation in Science Education. J. Responsible Innov. 2023 , 10 , 2198183. [ Google Scholar ] [ CrossRef ]
- Hadjichambis, A.C.; Georgiou, Y.; Paraskeva Hadjichambi, D.; Kyza, E.A.; Agesilaou, A.; Mappouras, D. Promoting RRI and Active Citizenship in an Inquiry-Based Controversial Socio-Scientific Issue: The Case of Cholesterol Regulation with Statins. J. Biol. Educ. 2019 , 53 , 548–560. [ Google Scholar ] [ CrossRef ]
- Itzek-Greulich, H.; Vollmer, C. Emotional and Motivational Outcomes of Lab Work in the Secondary Intermediate Track: The Contribution of a Science Center Outreach Lab. J. Res. Sci. Teach. 2017 , 54 , 3–28. [ Google Scholar ] [ CrossRef ]
- Maass, K.; Doorman, M.; Jonker, V.; Wijers, M. Promoting Active Citizenship in Mathematics Teaching. ZDM Math. Educ. 2019 , 51 , 991–1003. [ Google Scholar ] [ CrossRef ]
- Wiyarsi, A.; Prodjosantoso, A.K.; Nugraheni, A.R.E. Promoting Students’ Scientific Habits of Mind and Chemical Literacy Using the Context of Socio-Scientific Issues on the Inquiry Learning. Front. Educ. 2021 , 6 , 660495. [ Google Scholar ] [ CrossRef ]
- Ezquerra Martínez, Á.; Fernández-Sánchez, B. Analysis of Scientific Content of Advertising in the Press. Rev. Eureka Sobre Enseñ. Divulg. Las Cienc. 2014 , 11 , 275–289. [ Google Scholar ] [ CrossRef ]
- Elam, M.; Solli, A.; Mäkitalo, Å. Socioscientific Issues via Controversy Mapping: Bringing Actor-Network Theory into the Science Classroom with Digital Technology. Discourse 2019 , 40 , 61–77. [ Google Scholar ] [ CrossRef ]
- Solli, A.; Mäkitalo, Å.; Hillman, T. Rendering Controversial Socioscientific Issues Legible through Digital Mapping Tools. Int. J. Comput.-Support. Collab. Learn. 2018 , 13 , 391–418. [ Google Scholar ] [ CrossRef ]
- Ramnarain, U.; Moleki, B. Teachers’ Use of Newspaper Articles in Promoting a Humanistic Perspective of Science in South Africa. J. Sci. Teach. Educ. 2017 , 28 , 205–217. [ Google Scholar ] [ CrossRef ]
- Eidin, E.; Shwartz, Y. From Ideal to Practical—A Design of Teacher Professional Development on Socioscientific Issues. Sustainability 2023 , 15 , 11394. [ Google Scholar ] [ CrossRef ]
- Bolton, G. Changes in Thinking about Drama in Education. Theory Pract. 1985 , 24 , 151–157. [ Google Scholar ] [ CrossRef ]
- Becker, H.S. The Etiquette of Improvisation. Mind Cult. Act. 2000 , 7 , 171–176. [ Google Scholar ] [ CrossRef ]
- Choi, Y.; Lee, H. Exploring the Effects of Implementing a Research-Based Ssi Program on Students’ Understanding of Ssi and Willingness to Act. Asia-Pac. Sci. Educ. 2021 , 49 , 1–23. [ Google Scholar ] [ CrossRef ]
- Cornali, F.; Pomatto, G.; Agnella, S. Deliberating Science in Italian High School. The Case of the Scienza Attiva Project. J. Sci. Commun. 2017 , 16 , A02. [ Google Scholar ] [ CrossRef ]
- Holincheck, N.; Galanti, T.M.; Trefil, J. Assessing the Development of Digital Scientific Literacy with a Computational Evidence-Based Reasoning Tool. J. Educ. Comput. Res. 2022 , 60 , 1796–1817. [ Google Scholar ] [ CrossRef ]
- Kahn, S.; Zeidler, D.L. Using Our Heads and HARTSS*: Developing Perspective-Taking Skills for Socioscientific Reasoning (*Humanities, ARTs, and Social Sciences). J. Sci. Teach. Educ. 2016 , 27 , 261–281. [ Google Scholar ] [ CrossRef ]
- Kahn, S.; Zeidler, D.L. A Conceptual Analysis of Perspective Taking in Support of Socioscientific Reasoning. Sci. Educ. 2019 , 28 , 605–638. [ Google Scholar ] [ CrossRef ]
- Levy, B.L.M.; Oliveira, A.W.; Harris, C.B. The Potential of “Civic Science Education”: Theory, Research, Practice, and Uncertainties. Sci. Educ. 2021 , 105 , 1053–1075. [ Google Scholar ] [ CrossRef ]
- Ottander, K.; Simon, S. Learning Democratic Participation? Meaning-Making in Discussion of Socioscientific Issues in Science Education. Int. J. Sci. Educ. 2021 , 43 , 1895–1925. [ Google Scholar ] [ CrossRef ]
- Schenk, L.; Hamza, K.; Arvanitis, L.; Lundegard, I.; Wojcik, A.; Haglund, K. Socioscientific Issues in Science Education: An Opportunity to Incorporate Education about Risk and Risk Analysis? RISK Anal. 2021 , 41 , 2209–2219. [ Google Scholar ] [ CrossRef ]
- Sengul, O. Linking Scientific Literacy, Scientific Argumentation, and Democratic Citizenship. Univers. J. Educ. Res. 2019 , 7 , 1090–1098. [ Google Scholar ] [ CrossRef ]
- Yacoubian, H.A.; Khishfe, R. Argumentation, Critical Thinking, Nature of Science and Socioscientific Issues: A Dialogue between Two Researchers. Int. J. Sci. Educ. 2018 , 40 , 796–807. [ Google Scholar ] [ CrossRef ]
- du Preez, H.; van Niekerk, R. Utilising a Cultural-Historical Analysis to Map the Historicity of Social Studies, Natural Science and Technology Education in the Early Years. South Afr. J. Child. Educ. 2018 , 8 , 1–11. [ Google Scholar ] [ CrossRef ]
- Preez, H.D.; Joubert, I.; Middeljans, H. Discovering Child Citizens’ Understandings and Experiences of Social Justice. Citizsh. Teach. Learn. 2019 , 14 , 107–126. [ Google Scholar ] [ CrossRef ]
- Reis, P.; Tinoca, L.; Baptista, M.; Linhares, E. The Impact of Student-Curated Exhibitions about Socio-Scientific Issues on Students’ Perceptions Regarding Their Competences and the Science Classes. Sustainability 2020 , 12 , 2796. [ Google Scholar ] [ CrossRef ]
- Kilinc, A.; Demiral, U.; Kartal, T. Resistance to Dialogic Discourse in SSI Teaching: The Effects of an Argumentation-Based Workshop, Teaching Practicum, and Induction on a Preservice Science Teacher. J. Res. Sci. Teach. 2017 , 54 , 764–789. [ Google Scholar ] [ CrossRef ]
- Elías, M.; Pérez, J.; Cassot, M.D.R.; Carrasco, E.A.; Tomljenovic, M.; Zúñiga, E.A. Development of Digital and Science, Technology, Engineering, and Mathematics Skills in Chemistry Teacher Training. Front. Educ. 2022 , 7 , 932609. [ Google Scholar ] [ CrossRef ]
- Garik, P.; Benétreau-Dupin, Y. Report on a Boston University Conference December 7–8, 2012 on How Can the History and Philosophy of Science Contribute to Contemporary US Science Teaching? Sci. Educ. 2014 , 23 , 1853–1873. [ Google Scholar ] [ CrossRef ]
- Chou, P. The Representation of Global Issues in Taiwanese Elementary School Science Textbooks. Int. J. Sci. Math. Educ. 2021 , 19 , 727–745. [ Google Scholar ] [ CrossRef ]
- Van Harskamp, M.; Knippels, M.-C.P.J.; Boeve-de Pauw, J.N.A.; Van Joolingen, W.R. The Environmental Citizenship Opinions Questionnaire: A Self-Assessment Tool for Secondary Students. Front. Educ. 2023 , 8 , 1182824. [ Google Scholar ] [ CrossRef ]
- Arsingsamanan, W.; Sawangmek, S.; Nakkuntod, M. Development of Learning Management Model for Enhancing Scientific Citizenship of Upper Secondary School Students. Kasetsart J. Soc. Sci. 2023 , 44 , 163–168. [ Google Scholar ]
- Saunders, K.; Rennie, L. A Pedagogical Model for Ethical Inquiry into Socioscientific Issues In Science. Res. Sci. Educ. 2013 , 43 , 253–274. [ Google Scholar ] [ CrossRef ]
- Holstein, K.A.; Keene, K.A. The Complexities and Challenges Associated with the Implementation of a STEM Curriculum. Teach. Educ. Pract. 2013 , 26 , 616–636. [ Google Scholar ]
- Lundström, M.; Sjöström, J.; Hasslöf, H. Responsible Research and Innovation in Science Education: The Solution or The Emperor’s New Clothes? Sisyphus-J. Educ. 2017 , 5 , 11–27. [ Google Scholar ] [ CrossRef ]
- Snow, C.P. The Two Cultures and the Scientific Revolution ; Cambridge University Press: New York, NY, USA, 1963. [ Google Scholar ]
- Tedesco, J.C. Educar para la justicia social: Nuevos procesos de socialización, ciudadanía y educación en América Latina. Rev. IIDH 2010 , 52 , 231–2446. [ Google Scholar ]
- Katz-Buonincontro, J. Gathering STE(A)M: Policy, Curricular, and Programmatic Developments in Arts-Based Science, Technology, Engineering, and Mathematics Education Introduction to the Special Issue of Arts Education Policy Review: STEAM Focus. Arts Educ. Policy Rev. 2018 , 119 , 73–76. [ Google Scholar ] [ CrossRef ]
- Laherto, A.; Rasa, T. Facilitating Transformative Science Education through Futures Thinking. Horiz. Int. J. Learn. Futur. 2022 , 30 , 96–103. [ Google Scholar ] [ CrossRef ]
- Häggström, M.; Schmidt, C. Futures Literacy—To Belong, Participate and Act!: An Educational Perspective. Futures 2021 , 132 , 102813. [ Google Scholar ] [ CrossRef ]
Click here to enlarge figure | Question | Type of Response Sought | Rationale |
|---|
| RQ1. How many research reports are found in the Scopus and WoS databases from 2013 to 2023 on the use of socioscientific issues in classrooms? | Number of articles in Scopus; number of articles in WoS; number of duplicate articles; number of theoretical–conceptual articles; number of empirical research articles | Establish the extent of academic interest and research output on socioscientific issues in education over the last decade. | | RQ2. Which are the most cited articles and authors? | Most cited articles; most cited authors | Highlight the key contributions and influential researchers in the field. | | RQ3. What is the geographical distribution of the authors? | Countries of the lead authors | Reveal the global reach and diversity of research on socioscientific issues; indicate which regions might benefit from increased focus. | | RQ4. Which journals have published the most in this research area, and how are they categorized in terms of quartiles? | Leading journals and their corresponding quartiles | Indicate the academic credibility and impact of research on socioscientific issues, based on journal rankings and quartile categorizations. | | RQ5: What types of socioscientific questions predominate? | Thematic range, typology of socioscientific topics | Understand primary issues addressed in the literature (relevant contemporary topics). | | RQ6: What are the units of analysis in the empirical studies analyzed? What are the academic contexts where research on socioscientific issues is conducted? | Identification of units of analysis
and academic contexts | Understanding how socioscientific issues are being integrated into different educational contexts. | | RQ7: Which methodological approaches predominate (qualitative, quantitative or mixed)? | Number of qualitative, quantitative, and mixed research articles | Provide insight into how research on socioscientific issues is conducted. | | RQ8. Which teaching and learning models are identified in the analyzed studies? | Categorization of teaching and learning models | Demonstrate how socioscientific issues are being incorporated into teaching and learning practices. | | RQ9. What resources are used in the teaching and learning processes in the articles analyzed? | Categorization of resources in teaching and learning processes | Reveal the tools and materials that support the teaching and learning of socioscientific issues. | | RQ10: What forms of action and expression are used or developed in the teaching and learning processes in the studies analyzed? | Categorization of forms of action and expression used or developed in teaching and learning processes | Highlight how students and teachers engage with socioscientific issues through various activities. | | RQ11: What challenges are identified for teaching and learning when socioscientific issues are used? | Categorization of reported challenges | Provide a comprehensive view of potential obstacles and areas for improvement, essential for refining educational approaches to socioscientific issues. | | | Concept A
Socioscientific Issues | Concept B
Citizenship | Concept C
Education and Pedagogy |
|---|
OR
| “socio-scientific” OR
“socioscientific” | Citizen * | class OR classroom OR instruction OR instructional OR learning OR pedagogy OR teaching | | AND | | | | | Inclusion | Exclusion |
|---|
Year of publication 2013–2023.
Published articles.
Languages: Spanish and English. | Book chapters, Conference proceedings, Reviews, Letters, Editorials
Languages other than Spanish and English. | | | Empirical Articles | Theoretical-Conceptual Articles | Total |
|---|
| Scopus | 17 | 7 | 24 | | Web of Science | 25 | 8 | 33 | | Duplicate | 38 | 11 | 49 | | Total | 80 (75%) | 26 (25%) | 106 | | | Title | Author(s) | Journal | Year | Quotes | Type |
|---|
| 1 | Nature of Science, Scientific Inquiry, and Socioscientific Issues Arising from Genetics: A Pathway to Developing a Scientifically Literate Citizenry | Lederman et al. [ ] | Science & Education | 2014 | 119 quotes in WoS | Theoretical-conceptual | | 2 | Socioscientific Issues as a Vehicle for Promoting Character and Values for Global Citizens | Lee et al. [ ] | International Journal of Science Education | 2013 | 77 quotes in WoS | Empirical | | 3 | Citizen Science as a Distinct Field of Inquiry | Jordan et al. [ ] | Bioscience | 2015 | 67 quotes in WoS | Theoretical-conceptual | | | Title | Author(s) | Journal | Year | Quotes | Type |
|---|
| 1 | Socioscientific Issues as a Vehicle for Promoting Character and Values for Global Citizens | Lee et al.
[ ] | International Journal of Science Education | 2013 | 96 quotes in Scopus | Empirical | | 3 | Enhancing Student’s Communication Skills in the Science Classroom through Socioscientific Issues | Chung et al. [ ] | International Journal of Science and Mathematics Education | 2016 | 73 quotes in Scopus | Empirical | | 4 | Use of the concept of Bildung in the international science education literature, its potential, and implications for teaching and learning | Sjöström et al. [ ] | Studies in Science Education | 2017 | 66 quotes in Scopus | Theoretical-conceptual | | | Authors | Frequency as an Author in Scopus | Authors | Frequency as an Author in WoS |
|---|
| 1 | Dana L. Zeidler, Distinguished University Professor in Science Education in the College of Education at the University of South Florida. | 4 | Pedro Reis, Associate Professor at the Institute of Education at the University of Lisbon, Portugal. | 4 | | 2 | Ingo Eilks, Professor at the University of Bremen, Institute for Science Education, Germany. | 3 | Dana L. Zeidler, Distinguished University Professor in Science Education in the College of Education at the University of South Florida. | 4 | | 3 | Kyza, Eleni, Lecturer in the Department of Communication and Internet Studies, Cyprus University of Technology. | 3 | Kyza, Eleni, Lecturer in the Department of Communication and Internet Studies, Cyprus University of Technology. | 3 | | Ranking | Country of Origin of Articles | Number of Articles in WoS | % of a Total of 82 Results in WoS | Number of Articles in Scopus | % of a Total of 73 Results in Scopus |
|---|
| 1 | United States | 23 | 28% | 21 | 29% | | 2 | Spain | 11 | 13% | 12 | 16% | | 3 | Germany | 10 | 12% | 10 | 14% | | | Top Journals in WoS | Articles | Top Journals in Scopus | Articles | Duplicates
(Appearing in Both Databases) |
|---|
| #1 | Sustainability (Q1) | 11 | Sustainability (Q1) | 8 | 8 | | #2 | International Journal of Science Education (Q1) | 10 | International Journal of Science Education (Q1) | 7 | 7 | | #3 | Science Education (Q1) | 9 | International Journal of Science and Mathematics Education (Q1) | 4 | - | | Main Topics | Predominant Sub-Topics | Authors | Number of Articles | Mentions of School Subjects in Which These Topics Are Taught |
|---|
| I. Environmental issues | Climate change | Clausen [ ]; Eggert et al. [ ]; Feucht et al. [ ]; Gustafson and Öhman [ ]; Ho and Seow [ ]; Mang et al. [ ]; Namdar and Namdar [ ]; Park [ ]; Walsh and Tsurusaki [ ] | 9 | Geography (Clausen, [ ]; Ho and Seow, [ ]) | | | Healthy ecosystems and species preservation | Ariza et al. [ ]; Ginosar and Tal [ ]; Kinslow et al. [ ]; Liu et al. [ ]; Lebo et al. [ ]; McGregor et al. [ ]; Newton and Zeidler [ ] | 7 | (transdisciplinary approach, no mention of a specific subject) | | | Energy and resources | Birmingham and Calabrese Barton [ ]; Gulacar et al. [ ]; Nida et al. [ ]; Park [ ]; Ramírez and Chacón [ ]; Sakschewski et al. [ ]; Shasha-Sharf & Tal [ ] | 7 | Chemistry (Gulacar et al. [ ]; Nida et al. [ ])
Physics (Sakschewski et al. [ ]; Ramírez and Chacón [ ]) | | | Sustainable development | Cha et al. [ ]; Eilks [ ]; Zoller [ ] | 3 | Chemistry (Cha et al. [ ]; Eilks, [ ]) | | | Waste control | Fernández-Oliveras et al. [ ]; Lopez-Fernandez et al. [ ] | 2 | Chemistry (Lopez-Fernández et al. [ ]) | | II. Genetics | Genetics literacy, Genetic studies (genetic models, cells, and heredity), Genetically modified products | Aivelo and Uitto [ ]; Archila et al. [ ]; Cebesoy and Oztekin [ ]; Domènech-Casal [ ]; Goldschmidt et al. [ ]; Lederman [ ]; Lee et al. [ ]; McKnight et al. [ ]; Mehltretter Drury et al. [ ] | 9 | Biology (Aivelo and Uittlo [ ]; Goldschmidt et al. [ ]; McKnight et al. [ ], Mehltretter Drury et al. [ ]) | | III. Health | Health issues (use of laughing gas, scientific knowledge related to the human body, infectious diseases such as HIV/AIDS or COVID-19, health effects of nanoparticles) | Bayram-Jacobs et al. [ ]; Calvet et al. [ ]; Mnguni [ ]; Puig et al. [ ]; Senchina [ ]; Simonneaux et al. [ ] | 6 | Chemistry (Bayram-Jacobs et al. [ ])
Biology (Senchin, [ ]) | | IV. Local SSIs | Local/cultural socioscientific issues, Community-based socioscientific issues | Gormally and Heil [ ]; Kim et al. [ ]; Kinslow et al. [ ]; Ladachart and Ladachart [ ]; Moreno [ ]; Varis et al. [ ] | 6 | Biology (Gormann and Heil [ ]; Ladachart and Ladachart [ ])
Physics (Varis et al. [ ]) | | | Total number of articles addressing a predominant domain | | 49
(61% of 80 articles) | | | Subject | Number of Articles That Focus on a Specific Subject | Percentage of Articles That Focus on a Specific Subject |
|---|
| Biology | 11 | 38% | | Chemistry | 10 | 34% | | Geography | 3 | 10% | | Physics | 3 | 10% | | Mathematics | 2 | 8% | | Total number of articles that focus on a specific subject | 29 | 100% | | Categories of Units of Analysis | Number of Items | Percentage of Articles |
|---|
| | 51 | 68% | | | 15 | 20% | | | 3 | 4% | | | 6 | 8% | | Total number of empirical articles that make use of one of the four categories of units of analysis | 75 | 100% | Type of Teacher Education
(Unit of Analysis) | Authors |
|---|
Pre-service science teachers
(9 articles) | Avsar Erumit and Yuksel [ ], Ladachart and Ladachart [ ], Nida et al. [ ], Palma-Jiménez et al. [ ], Park [ ], Pitiporntapin et al. [ ], Rundgren and Chang Rundgren [ ], Zoller [ ], Salcedo-Armijo et al. [ ] | Pre-service and in-service science teachers
(5 articles) | Ariza et al. [ ], Rundgren and Chang Rundgren [ ], Shasha-Sharf and Tal [ ], van der Leij et al. [ ], Georgiou and Kyza [ ] | In-service science teachers
(1 article) | Cebesoy and Oztekin [ ] | | School Level at Which the Empirical Work Is Located | Number of Items | Percentage of Articles |
|---|
| Primary (elementary school) | 6 | 9% | | Secondary (middle school, initial secondary education) | 11 | 16% | | Upper secondary (high school, preparatory education) | 31 | 45% | | Post-secondary (pre-service teacher education) | 15 | 21% | | Post-secondary (college, undergraduate students) | 6 | 9% | | Total number of empirical articles in which a specific school level is investigated | 69 | 100% | | Approach | Number of Items | Percentage of Articles |
|---|
| Qualitative | 36 | 45% | | Mixed | 22 | 27.5% | | Quantitative | 22 | 27.5% | | Total number of empirical articles | 80 | 100% | | Pedagogical Models | Authors Researching or Using the Pedagogical Model | Number of Articles Analyzing Pedagogical Models | Percentage of Articles Analyzing Pedagogical Models |
|---|
| Inquiry-based learning (IBL)/socioscientific inquiry-based learning (SSIBL) | Ariza et al. [ ], Bardone et al. [ ], Georgiou and Kyza [ ], Hadjichambis et al. [ ], Itzek-Greulich and Vollmer [ ], Maass et al. [ ], Maass et al. [ ], Mang et al. [ ], McGregor et al. [ ], McKnight et al. [ ], Rundgren and Chang Rundgren [ ], van der Leij et al. [ ], Wiyarsi et al. [ ] | 13 | 57% | | Problem-based, context-based and case-based learning | Chaudhry et al. [ ], Chaudhry et al. [ ], Chung et al. [ ]
Eilks [ ], Lopez-Fernandez et al. [ ], Mnguni [ ], Varis et al. [ ], Wiyarsi et al. [ ] | 8 | 35% | | Model-based learning | Avsar Erumit and Yuksel [ ], Maass et al. [ ] | 2 | 9% | | Total number of articles that analyze or apply one of the identified pedagogical models | | 23 | 100% | | Resources | Article |
|---|
| Journalistic texts/news and/or advertising texts | Ginosar and Tal [ ], Puig, et al. [ ], Fernández-Oliveras et al. [ ], Ezquerra Martínez and Fernández-Sánchez [ ], Ramnarain and Moleki [ ], Moreno [ ], Feucht et al. [ ] | | Digital data mapping and visualization resources | Eggert et al. [ ], Elam et al. [ ], Fernández-Oliveras et al. [ ], Gulacar et al. [ ], Solli et al. [ ] | | Technique | Article | Number of Articles Identified |
|---|
| Debate, discussion techniques, deliberative democracy, negotiation | Archila et al. [ ], Avsar Erumit and Yuksel [ ], Bayram-Jacobs et al. [ ], Chowdhury et al. [ ], Chowdhury et al. [ ], Chung et al. [ ], Cornali et al. [ ], Eggert et al. [ ], Eidin and Shwartz [ ], Feucht et al. [ ], Goldschmidt et al. [ ], Gustafsson and Öhman [ ], Holincheck et al. [ ], Kahn and Zeidler [ ], Kahn and Zeidler [ ], Lee and Tran [ ], Levy et al. [ ], Lopez-Fernandez et al. [ ], Mang et al. [ ], Mehltretter Drury et al. [ ], Newton and Zeidler [ ], Nida et al. [ ], Ottander and Simon [ ], Palma-Jiménez et al. [ ], Pitiporntapin et al. [ ], Puig et al. [ ], Rundgren and Chang Rundgren [ ], Sakschewski et al. [ ], Schenk et al. [ ], Sengul [ ], Shasha-Sharf and Tal [ ], Simonneaux et al. [ ], Sjöström et al. [ ], van der Leij et al. [ ], Wiyarsi et al. [ ], Yacoubian and Khishfe [ ] | 36 | | Drama and role-playing | Archila et al. [ ], Birmingham et al. [ ], Chowdhury et al. [ ], Chung et al. [ ], Cornali et al. [ ], du Preez and van Niekerk [ ], Fernández-Oliveras et al. [ ], Kahn and Zeidler [ ], Kahn and Zeidler [ ], Lebo et al. [ ], Mang et al. [ ], McGregor et al. [ ], McKnight et al. [ ], Mnguni [ ], Nida et al. [ ], Namdar and Namdar [ ], Preez et al. [ ], Ramnarain and Moleki [ ], Simonneaux et al. [ ], Sjöström et al. [ ] | 20 | | Drawing | Ariza et al. [ ], Cha et al. [ ], Preez et al. [ ], Reis et al. [ ] | 4 | | Level at Which the Challenge Is Presented | Challenge | Articles that Mention the Challenge |
|---|
| Teaching Practice | Resistance to the shift from monological to dialogic discourse despite attempts at professional development. | Eidin and Shwartz, [ ]; Kilinc et al. [ ] | | | Teaching ethical challenge: Difficulties in dealing with personal values and beliefs and the ethical aspects of science. | Ariza et al. [ ] | | | Limited knowledge or understanding of the causes and consequences of socioscientific issues in all their complexity. | Eggert et al. [ ]; Cebesoy and Oztekin [ ] | | Teacher Training | Lack of an explicit association with STEM competencies in the teacher education curriculum. | Elias et al. [ ]; Palma-Jiménez et al. [ ] | | | Lack of linkage of socioscientific issues with scientific concepts in teacher training. | Saunders and Rennie [ ]; Pitiporntapin et al. [ ]; Elias et al. [ ] | | | Lack of preparation to address emotional issues in teacher training: Lack of awareness of teachers to the emotions that can be generated among students who face controversial issues. | Hodson [ ] | | Students | Lack of prior or basic knowledge of socioscientific issues and insufficient media literacy. | Pitiporntapin et al. [ ]; Ginosar and Tal [ ] | | | Lack of intellectual depth on social issues (multiculturalism, human rights, social justice). | Chou [ ]; Van Harskamp et al. [ ] | | | Insufficient emotional literacy. Lack of emotional abilities to deal with stressful learning situations. | Walsh and Tsurusaki [ ]; Hodson [ ]; van der Leij et al. [ ] | | Curricula | Failure to incorporate the concept of future risk or future consequences into school science education. | Bardone et al. [ ]; Schenk et al. [ ]; Eggert et al. [ ]; Chou [ ]; Eidin and Shwartz [ ] | | | Curricular restrictions and the existence of high-stakes exams. A disciplinary approach to science education. | Garik and Benétreau-Dupin [ ], Zoller [ ], Cebesoy and Oztekin [ ]; Ariza et al. [ ] | | | Lack of an action-focused approach to education: Curricula that are not focused on areas of knowledge to inform democratically accountable actions. | Arsingsamanan et al. [ ]; Birmingham and Calabrese Barton [ ]; Chowdhury et al. [ ] | | The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
Share and CiteViehmann, C.; Fernández Cárdenas, J.M.; Reynaga Peña, C.G. The Use of Socioscientific Issues in Science Lessons: A Scoping Review. Sustainability 2024 , 16 , 5827. https://doi.org/10.3390/su16145827 Viehmann C, Fernández Cárdenas JM, Reynaga Peña CG. The Use of Socioscientific Issues in Science Lessons: A Scoping Review. Sustainability . 2024; 16(14):5827. https://doi.org/10.3390/su16145827 Viehmann, Cristina, Juan Manuel Fernández Cárdenas, and Cristina Gehibie Reynaga Peña. 2024. "The Use of Socioscientific Issues in Science Lessons: A Scoping Review" Sustainability 16, no. 14: 5827. https://doi.org/10.3390/su16145827 Article MetricsArticle access statistics, further information, mdpi initiatives, follow mdpi.  Subscribe to receive issue release notifications and newsletters from MDPI journals  STEM Education - {{newsColumn.name}}
- Share facebook twitter google linkedin
 Solving word problems involving triangles and implications on training pre-service mathematics teachers- William Guo ,
- School of Engineering and Technology, Central Queensland University, North Rockhampton, QLD 4702, Australia
- Academic Editor: Zlatko Jovanoski
- Received: 18 June 2024 Revised: 02 July 2024 Accepted: 05 July 2024 Published: 09 July 2024
- Full Text(HTML)
- Download PDF
Triangles and trigonometry are always difficult topics for both mathematics students and teachers. Hence, students' performance in solving mathematical word problems in these topics is not only a reflection of their learning outcomes but also an indication of teaching effectiveness. This case study drew from two examples of solving word problems involving triangles by pre-service mathematics teachers in a foundation mathematics course delivered by the author. The focus of this case study was on reasoning implications of students' performances on the effective training of pre-service mathematics teachers, from which a three-step interactive explicit teaching-learning approach, comprising teacher-led precise and inspiring teaching (or explicit teaching), student-driven engaged learning (or imitative learning), and student-led and teacher-guided problem-solving for real-world problems or projects (or active application), was summarized. Explicit teaching establishes a solid foundation for students to further their understanding of new mathematical concepts and to conceptualize the technical processes associated with these new concepts. Imitative learning helps students build technical abilities and enhance technical efficacy by engaging in learning activities. Once these first two steps have been completed, students should have a decent understanding of new mathematical concepts and technical efficacy to analyze, formulate, and finally solve real-world applications with assistance from teachers whenever required. Specially crafted professional development should also be considered for some in-service mathematics teachers to adopt this three-step interactive teaching-learning process. - pre-service mathematics teacher ,
- word problem ,
- triangles ,
- problem-solving ,
- explicit teaching ,
- imitated learning ,
- active applications ,
- professional development
Citation: William Guo. Solving word problems involving triangles and implications on training pre-service mathematics teachers[J]. STEM Education, 2024, 4(3): 263-281. doi: 10.3934/steme.2024016 Related Papers: | [1] | , 2016, 47(7): 1028-1047. http://doi.org/10.1080/0020739X.2016.1155774 --> Koyunkaya, M.Y., Mathematics education graduate students' understanding of trigonometric ratios. , 2016, 47(7): 1028-1047. http://doi.org/10.1080/0020739X.2016.1155774 doi: | | [2] | , 2018, 6(1): 58-78. http://doi.org/10.18404/ijemst.328344 --> Koyunkaya, M.Y., An examination of a pre-service mathematics teacher's mental constructions of relationships in a right triangle. , 2018, 6(1): 58-78. http://doi.org/10.18404/ijemst.328344 doi: | | [3] | , 2019, 14(2): 72-91. https://doi.org/10.1016/j.teln.2018.11.004 --> Ngcobo, A.Z., Madonsela, S.P. and Brijlall, D., The teaching and learning of trigonometry. , 2019, 14(2): 72-91. https://doi.org/10.1016/j.teln.2018.11.004 doi: | | [4] | , 2022, 10(2): 208-224. https://doi.org/10.30935/scimath/11716 --> Durmaz, A.B. and Bostan, I.M., Pre-service teachers' knowledge regarding the area of triangle. , 2022, 10(2): 208-224. https://doi.org/10.30935/scimath/11716 doi: | | [5] | , 2018, 39: 171–196. https://doi.org/10.1007/s13138-017-0123-y --> Rellensmann, J. and Schukajlow, S., Do students enjoy computing a triangle's side? Enjoyment and boredom while solving problems with and without a connection to reality from students' and pre-service teachers' perspectives. , 2018, 39: 171–196. https://doi.org/10.1007/s13138-017-0123-y doi: | | [6] | , 2017, 5(1): 28-42. https://doi.org/10.30935/scimath/9495 --> Fyhn, A.B., What happens when a climber falls? Young climbers mathematise a climbing situation. , 2017, 5(1): 28-42. https://doi.org/10.30935/scimath/9495 doi: | | [7] | , 2023, 11(2): 249-258. https://doi.org/10.30935/scimath/12582 --> Guo, W., Solving word problems involving triangles by transitional engineering students: Learning outcomes and implications. , 2023, 11(2): 249-258. https://doi.org/10.30935/scimath/12582 doi: | | [8] | , 2015, 11(6): 1379-1397. https://doi.org/10.12973/eurasia.2015.1396a --> Dündar, S., Mathematics teacher-candidates' performance in solving problems with different representation styles: The trigonometry example. , 2015, 11(6): 1379-1397. https://doi.org/10.12973/eurasia.2015.1396a doi: | | [9] | , 2017, 36(3): 273-306. https://doi.org/10.1080/03323315.2017.1327361 --> Walsh, R., Fitzmaurice, O. and O'Donoghue, J., What subject matter knowledge do second-level teachers need to know to teach trigonometry? An exploration and case study. , 2017, 36(3): 273-306. https://doi.org/10.1080/03323315.2017.1327361 doi: | | [10] | , 2018, 9(1): 169-182. https://doi.org/10.22342/jme.9.2.5261.169-182 --> Nabie, M. J., Akayuure, P., Ibrahim-Bariham, U.A. and Sofo, S., Trigonometric concepts: Pre-service teachers' perceptions and knowledge. , 2018, 9(1): 169-182. https://doi.org/10.22342/jme.9.2.5261.169-182 doi: | | [11] | , 2021, 53(8): 2004–2025. https://doi.org/10.1080/0020739X.2020.1857858 --> Ubah, I., Pre-service mathematics teachers' semiotic transformation of similar triangles: Euclidean geometry. , 2021, 53(8): 2004–2025. https://doi.org/10.1080/0020739X.2020.1857858 doi: | | [12] | , 2022, 10(20): 3786. http://doi.org/10.3390/math10203786 --> Guo, W., Exploratory case study on solving word problems involving triangles by pre-service mathematics teachers in a regional university in Australia. , 2022, 10(20): 3786. http://doi.org/10.3390/math10203786 | | [13] | , 2024, 16(1): 58-68. https://doi.org/10.69721/TPS.J.2024.16.1.07 --> Pentang J.T., Andrade, L.J.T., Golben, J.C., Talua, J.P., Bautista, R.M., Sercenia, J.C., et al., Problem-solving difficulties, performance, and differences among preservice teachers in Western Philippines University. , 2024, 16(1): 58-68. https://doi.org/10.69721/TPS.J.2024.16.1.07 doi: | | [14] | , 2020, Pearson. --> Christensen, L.B., Johnson, R.B., Turner, L.A. and Christensen, L.B., , 2020, Pearson. | | [15] | , 2 ed. 2020, Melbourne, Australia: Pearson. --> Guo, W.W., , 2 ed. 2020, Melbourne, Australia: Pearson. | | [16] | , 2022, 10(16): 2862. https://doi.org/10.3390/math10162862 --> Rézio, S., Andrade, M.P. and Teodoro, M.F., Problem-based learning and applied mathematics. , 2022, 10(16): 2862. https://doi.org/10.3390/math10162862 doi: | | [17] | , 2023. https://doi.org/10.1007/s13394-023-00468-8 --> Gómez-Chacón, I.M., Bacelo, A., Marbán, J.M. and Palacios, A., Inquiry-based mathematics education and attitudes towards mathematics: tracking profiles for teaching. , 2023. https://doi.org/10.1007/s13394-023-00468-8 doi: | | [18] | , 1984, 77(6): 351-359. https://doi.org/10.1080/00220671.1984.10885555 --> Darch, C., Carnine D. and Gersten, R., Explicit instruction in mathematics problem solving. , 1984, 77(6): 351-359. https://doi.org/10.1080/00220671.1984.10885555 doi: | | [19] | , 2004,104(3): 233–251. https://doi.org/10.1086/499751 --> Kroesbergen, E.H., Van Luit, J.E.H. and Maas, C.J.M., Effectiveness of explicit and constructivist mathematics instruction for low-achieving students in The Netherlands. , 2004,104(3): 233–251. https://doi.org/10.1086/499751 doi: | | [20] | , 2015,115: 303–333. https://doi.org/10.1086/679969 --> Doabler, C.T., Baker, S.K., Kosty, D.B., Smolkowski, K., Clarke, B., Miller, S.J., et al., Examining the association between explicit mathematics instruction and student mathematics achievement. , 2015,115: 303–333. https://doi.org/10.1086/679969 doi: | | [21] | , 2021, 44(2-3): 267-283. https://doi.org/10.1007/s40614-021-00291-1 --> Gunn, B., Smolkowski, K., Strycker, L.A. and Dennis, C., Measuring Explicit Instruction Using Classroom Observations of Student-Teacher Interactions (COSTI). , 2021, 44(2-3): 267-283. https://doi.org/10.1007/s40614-021-00291-1 doi: | | [22] | , April 2024. Available from: . --> Evans, T., We need to go back to teacher-led explicit instruction: maths expert. , April 2024. Available from: . | | [23] | , 2018, 5(6): 2349–5219. --> Magbanua, M.U., Explicit instruction in problem-solving skills, creative and critical thinking skills of the elementary education students. , 2018, 5(6): 2349–5219. | | [24] | , 2022, 6(5): 7781–7787. --> Joaquin, C.J.A., A guided-discovery approach to problem solving: An explicit instruction. , 2022, 6(5): 7781–7787. | | [25] | , 2021, 9(14): 1623. https://doi.org/10.3390/math9141623 --> Guo, W., Li, W. and Tisdell, C.C., Effective pedagogy of guiding undergraduate engineering students solving first-order ordinary differential equations. , 2021, 9(14): 1623. https://doi.org/10.3390/math9141623 doi: | | [26] | , 2024, 12(1): 71-84. https://doi.org/10.30935/scimath/13831 --> Guo, W., Special tutorials to support pre-service mathematics teachers learning differential equations and mathematical modelling. , 2024, 12(1): 71-84. https://doi.org/10.30935/scimath/13831 doi: | | [27] | , 2022, 2(3): 221-244. https://doi.org/10.3934/steme.2022014 --> Evans, T. and Dietrich, H., Inquiry-based mathematics education: a call for reform in tertiary education seems unjustified. , 2022, 2(3): 221-244. https://doi.org/10.3934/steme.2022014 doi: | - This work is licensed under a Creative Commons Attribution-NonCommercial-Share Alike 4.0 Unported License. To view a copy of this license, visit http://creativecommons.org/licenses/by-nc-sa/4.0/ -->
SupplementsAccess HistoryReader Comments- © 2024 the Author(s), licensee AIMS Press. This is an open access article distributed under the terms of the Creative Commons Attribution License ( http://creativecommons.org/licenses/by/4.0 )
沈阳化工大学材料科学与工程学院 沈阳 110142  Article views( 66 ) PDF downloads( 5 ) Cited by( 0 ) Figures and Tables Figures( 5 ) / Tables( 3 )  Associated materialOther articles by authors. Related pages- on Google Scholar
- Email to a friend
- Order reprints
Export File - Figure 1. A sketch of isosceles triangle for the first word problem
- Figure 2. A reworked sketch for the second problem with derived angles (in red)
- Figure 3. The first reworked sketch for solving the second problem through right triangles
- Figure 4. The second reworked sketch for solving the second problem through right triangles
- Figure 5. The third reworked sketch for solving the second problem through right triangles
 - University of Colorado Boulder
- Monday, July 15
Frugal Science—a free public lectureMonday, July 15, 2024 7pm to 8pm - Share Frugal Science—a free public lecture on Facebook
- Share Frugal Science—a free public lecture on Twitter
- Share Frugal Science—a free public lecture on LinkedIn
 About this Event 2000 Colorado Avenue, Boulder, CO 80309 The Boulder School for Condensed Matter and Materials Physics presents a public lecture: Frugal Science: A Physicist View on Tackling Global Health, Climate Change and Democratization of Science Manu Prakash, Stanford University Abstract: Science faces an accessibility challenge. Although information/knowledge is fast becoming available to everyone around the world, the experience of science is significantly limited. One approach to solving this challenge is to democratize access to scientific tools. We believe this can be achieved via “Frugal science”; a philosophy that inspires design, development and deployment of ultra-affordable yet powerful scientific tools for the masses. Using direct examples linking soft-matter physics as an inspiration for solutions to societal challenges - we will walk through problems in the domain of global health, climate change and science education. We will show how a trick from Astronomy inspires a new malaria diagnostics. How understanding micro-scale hydrodynamics of a human parasite enables us to mitigate spread of Schistosomiasis. How understanding percolation in entangled networks enables production of bio-degradable menstrual pads. Or understanding the rheology of marine snow enables us to better estimate carbon capture in our vast oceans. And how origami inspired manufacturing techniques can bring access to microscopy to millions of kids around the world. By connecting the dots between science education, ecological monitoring and global health, we will explore the role of “simple” tools in advancing access to better planetary health in a resource limited world. Manu Prakash is an Associate Professor in the Department of Bioengineering at Stanford University spanning the schools of engineering, medicine, and sustainability. He runs a curiosity-driven lab at Stanford combining his passion for basic science while also inventing ultra-affordable and accessible technologies. His numerous inventions include Foldscope (a one-dollar origami microscope), Paperfuge (a 20-cent centrifuge), Abuzz (a cellphone app for identifying mosquitoes) and Octopi (a malaria diagnostics tool). Manu grew up in India and got his PhD from MIT, was a Junior Fellow at Harvard Society of Fellows and a 2016 MacArthur Fellow. Sponsored by the Boulder School for Condensed Matter and Materials Physics, the National Science Foundation, and the University of Colorado Boulder Physics Dept. For more information visit boulderschool.yale.edu Event DetailsCollege, School & Unit  4 people are interested in this event Your browser does not support iframes. User Activity No recent activity Campus Events Calendar The Campus Events Calendar is provided by Strategic Relations and Communications  |

































































IMAGES
VIDEO
COMMENTS
The scientific method. At the core of biology and other sciences lies a problem-solving approach called the scientific method. The scientific method has five basic steps, plus one feedback step: Make an observation. Ask a question. Form a hypothesis, or testable explanation. Make a prediction based on the hypothesis.
The scientific method. At the core of physics and other sciences lies a problem-solving approach called the scientific method. The scientific method has five basic steps, plus one feedback step: Make an observation. Ask a question. Form a hypothesis, or testable explanation. Make a prediction based on the hypothesis.
Use this collection of example worked chemistry problems with answers to learn problem-solving skills and how to use formulas.
Scientific Problem Solving Humans have always wondered about the world around them. One of the questions of interest was (and still is): what is this world made of? Chemistry has been defined in various ways as the study of matter. What matter consists of has been a source of debate over the centuries.
Need help with your physics homework? This is a collection of worked example physics problems and solutions you can study or use when doing problem sets.
Problem Solving in STEM. Solving problems is a key component of many science, math, and engineering classes. If a goal of a class is for students to emerge with the ability to solve new kinds of problems or to use new problem-solving techniques, then students need numerous opportunities to develop the skills necessary to approach and answer ...
There are many fun science experiments that you can do with your children to help them develop problem-solving skills. For example, you can create a homemade volcano, make slime, or build a simple machine. These experiments allow children to learn by doing and encourage them to think creatively.
A scientific problem can be solved using the steps of the scientific method. Learn how to identify a scientific problem, how to conduct a scientific experiment, and understand how to choose the ...
In your study of philosophy, you will explore deeper questions about science. For example, are there any forms of knowledge that are nonscientific? Can science tell us what we ought to do? Can logical and mathematical truths be proven in a scientific way?
Science Problem Solving Activities. Chris has a master's degree in history and teaches at the University of Northern Colorado. Problem solving is an essential skill for scientists, but thinking in ...
The processes of problem-solving and decision-making can be complicated and drawn out. In this article we look at how the scientific method, along with deductive and inductive reasoning can help simplify these processes.
Science fair projects that solve problems in the real world allow students to test their interest and aptitude for STEM careers.
A useful problem-solving strategy was presented for use with these equations and two examples were given that illustrated the use of the strategy. Then, the application of the kinematic equations and the problem-solving strategy to free-fall motion was discussed and illustrated. In this part of Lesson 6, several sample problems will be presented.
A problem-solving experiment is a learning activity that uses experimental design to solve an authentic problem. It combines two evidence-based teaching strategies: problem-based learning and inquiry-based learning. The use of problem-based learning and scientific inquiry as an effective pedagogical tool in the science classroom has been well established and strongly supported by research ...
The problem-solving process typically includes the following steps: Identify the issue: Recognize the problem that needs to be solved. Analyze the situation: Examine the issue in depth, gather all relevant information, and consider any limitations or constraints that may be present. Generate potential solutions: Brainstorm a list of possible ...
Invention and problem-solving aren't just for laboratory thinkers hunkered down away from the classroom. Students from elementary to high school can wonder, design, and invent a real product that solves real problems. "Problem-solving involves finding answers to questions and solutions for undesired effects.
Engaging learners in the excitement of science, helping them discover the value of evidence-based reasoning and higher-order cognitive skills, and teaching them to become creative problem solvers have long been goals of science education reformers. But the means to achieve these goals, especially methods to promote creative thinking in scientific problem solving, have not become widely known ...
Computer science is similar to mathematics in that both are used as a means of defining and solving some problem. In fact, computer-based applications often use mathematical models as a basis for the manner in which they solve the problem at hand.
In this work, we approach the task of identifying problem-solving patterns in scientific text. We choose to use the model of problem-solving described by Hoey ( 2001 ). This pattern comprises four parts: Situation, Problem, Response and Evaluation.
Problem-solving skills are valuable soft skills that help you identify the root of a problem, analyze potential solutions, and decide what to do.
Real world problems are issues and risks that are causing losses or are likely to cause losses in the near future. This term is commonly used in science, mathematics, engineering, design, coding and other fields whereby students may be asked to propose solutions to problems that are currently relevant to people and planet as opposed to theoretical, insignificant or personal problems. The ...
4. Relax one assumption at a time from the problem statement (to make the problem easier) Many problems are too hard to solve on their own. However, by solving a easier, related problem, you can ...
My thoughts on how data scientists solve problems, along with sharing a case study using one favorite project in my first job
In new research, mathematicians have narrowed down one of the biggest outstanding problems in math. Huge breakthroughs in math and science are usually the work of many people over many years ...
Diversity invigorates problem solving. Science benefits greatly from a community that approaches problems in a variety of creative ways. A diverse community is better able to generate new research methods, explanations, and ideas, which can help science over challenging hurdles and shed new light on problems.
Welcome to the daily solving of our PROBLEM OF THE DAY with Jay Dalsaniya We will discuss the entire problem step-by-step and work towards developing an optimized solution. This will not only help you brush up on your concepts of Tree but also build up problem-solving skills. Given a binary tree and an integer target, check whether there is a root-to-leaf path with its sum as target.
Socioscientific issues represent an innovative approach within the realm of STEM education as they integrate real-world problems, promote critical thinking, and encourage interdisciplinary learning, thus preparing students to address complex societal challenges through scientific inquiry. The objective of this scoping review was to analyze the use of SSIs in science lessons.
Triangles and trigonometry are always difficult topics for both mathematics students and teachers. Hence, students' performance in solving mathematical word problems in these topics is not only a reflection of their learning outcomes but also an indication of teaching effectiveness. This case study drew from two examples of solving word problems involving triangles by pre-service mathematics ...
Using direct examples linking soft-matter physics as an inspiration for solutions to societal challenges - we will walk through problems in the domain of global health, climate change and science education. We will show how a trick from Astronomy inspires a new malaria diagnostics.