The Dining Philosophers problem and different ways of solving it

The problem
Avoiding the deadlock with a semaphore, one philosopher can just be left-handed, even more efficient solution.
Templates (for web app):
8.5. Dining Philosophers Problem and Deadlock ¶
The previous chapter introduced the concept of deadlock . Deadlock is the permanent blocking of two or more threads based on four necessary conditions. The first three are general properties of synchronization primitives that are typically unavoidable. The last is a system state that arises through a sequence of events.
Mutual exclusion : Once a resource has been acquired up to its allowable capacity, no other thread is granted access. No preemption : Once a thread has acquired a resource, the resource cannot be forcibly taken away. For instance, only the owner of a mutex can unlock it. Hold and wait : It is possible that a thread can acquire one resource and retain ownership of that resource while waiting on another. Circular wait : One thread needs a resource held by another, while this second thread needs a different resource held by the first.

Figure 8.5.1: Providing the same number of plates and forks creates a problem for a set of dining philosophers
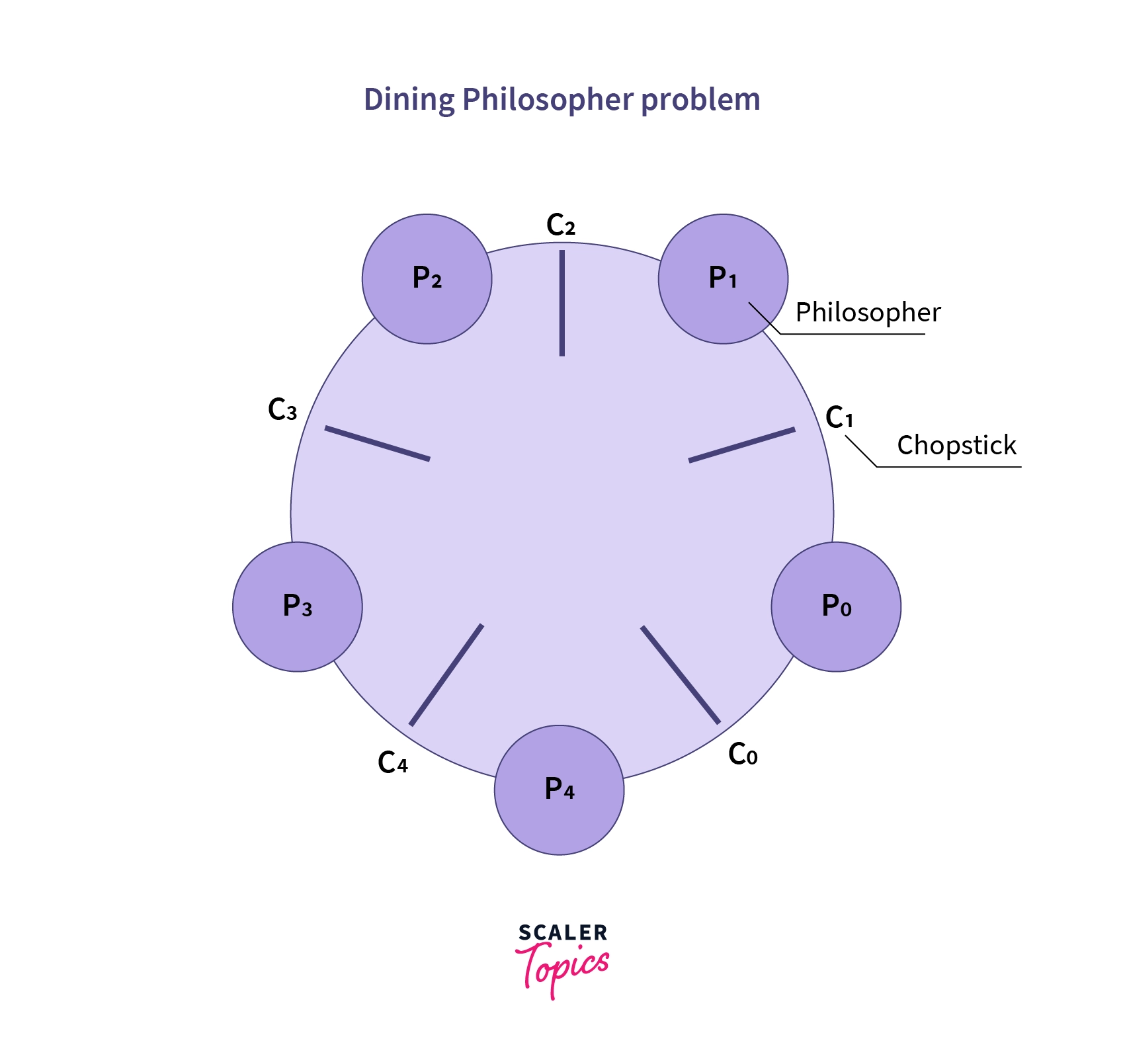
The dining philosophers problem is a metaphor that illustrates the problem of deadlock. The scenario consists of a group of philosophers sharing a meal at a round table. As philosophers, they like to take some time to think; but they are at a meal, so they also need to eat. As illustrated in Figure 8. , there is a large serving dish in the middle of the table. Every philosopher has a plate and two serving forks, one to their right and one to their left. When a philosopher decides that they are hungry enough, they stop thinking and grab the forks to serve themselves from the serving dish in the middle.
The problem arises when all of the philosophers decide to eat at the same time. Consider the case where all of the philosophers independently decide that they will try to grab the fork to their left first. When this happens, assuming all of the places at the table are occupied, then all of the forks have been taken. That is, each of the five forks shown are to the left of exactly one of the five philosophers. At this point, every philosopher has exactly one fork, but there are none available for anyone to get their second fork. Unless one of the philosophers decides to give up on eating and put a fork down, all of the philosophers will starve.
Code Listing 8.24 illustrates how this scenario translates into code with semaphores. Multiple philosopher threads share an array of N fork semaphores (numbered 0 through N-1) and each thread tries to acquire two of them. Thread 0 waits on semaphores 0 and 1, thread 1 waits on semaphores 1 and 2, and so on, until thread N-1 waits on semaphores N-1 and 0 (since the modulus operator is applied).
| /* Code Listing 8.24: The dining philosophers problem in code with semaphores */ void * philosopher (void * _args) { /* Cast the args as struct with self identifier, semaphores */ struct args *args = (struct args *) _args; int self = args->self; /* unique thread identifier */ int next = (self + 1) % SIZE; sem_wait (args->sems[self]); /* pick up left fork */ sem_wait (args->sems[next]); /* pick up right fork */ /* Critical section (eating) */ sem_post (args->sems[next]); /* put down right fork */ sem_post (args->sems[self]); /* put down left fork */ /* Do other work and exit thread */ } |
Assuming they are initialized to 1 and the standard sem_wait() is used, semaphores exhibit the three required system features of deadlock. They enforce mutual exclusion because the second thread to attempt to down the semaphore will become blocked since the internal value would be negative. Since the threads can acquire one and get blocked trying to acquire the second semaphore, they satisfy the hold-and-wait criterion. And since no thread can break another thread’s claim to a semaphore, the no preemption criterion is met. The fourth criterion for deadlock, circular wait, arises from the sequence in which the threads wait on the respective semaphores. Every philosopher is waiting on the fork to their right, which has been grabbed by someone else as their left fork.

Example 8.5.1
Table 8.1 illustrates how the circular wait arises. Every thread successfully waits on one semaphore and gets blocked by the second.
| Thread 0 | Thread 1 | Thread 2 | Thread 3 | Thread 4 |
|---|---|---|---|---|
| sem_wait(0); SUCCESS sem_wait(1); BLOCKED | sem_wait(1); SUCCESS sem_wait(2); BLOCKED | sem_wait(2); SUCCESS sem_wait(3); BLOCKED | sem_wait(3); SUCCESS sem_wait(4); BLOCKED | sem_wait(4); SUCCESS sem_wait(0); BLOCKED |
Table 8.1: If all threads get through the first semaphore, no one gets by the second
It is important to note that this problem applies to other synchronization primitives, not just semaphores. That is, locks and condition variables also meet the system requirements for deadlock. To illustrate how this problem could arise in practice with locks, consider the software that links incoming and outgoing connections in a network switch. In this scenario, assume that each thread responsible for forwarding data packets acquires locks on dedicated physical ports. As such, the software maintains an array of locks nic_locks . There is no assumption that the ports need to be adjacent; instead, the switch code just grabs any two that are available. Code Listing 8.25 shows a simplistic approach that fits the dining philosophers structure. The first loop iterates through the locks until one is assigned to be this thread’s incoming port; the second loop acquires the outgoing port. To make matters worse, these two loops may be in different portions of the code base, so someone reviewing the code may not think they are actually connected in this way !
| /* Code Listing 8.25: It is easy to fall into the dining philosophers structure without realizing it */ while (true) { in++; in %= NUMBER_OF_PORTS; if (!pthread_mutex_trylock (nic_locks[in])) break; } /* successfully locked network card in for incoming data */ while (true) { out++; out %= NUMBER_OF_PORTS; if (!pthread_mutex_trylock (nic_locks[out])) break; } /* successfully locked network card out for outgoing data */ |
8.5.1. Solution of Limiting Accesses ¶
One approach to solving the dining philosophers problem is to employ a multiplexing semaphore to limit the number of concurrent accesses. To return to the original metaphor, this solution would require that one of the seats at the table must always remain unoccupied. Assuming all of the philosophers try to grab their left fork first, the fork to the left of the empty seat would not be claimed. Consequently, the philosopher to the left of that seat could grab the fork as their second, as it is the fork to their left. After this philosopher eats, they can put both forks down, making their left fork available as the right fork for the next philosopher.
Code Listing 8.26 shows how to incorporate this approach into the structure of Code Listing 8.24 . A single additional semaphore ( can_sit ) is created and initialized to N-1 for N semaphores. This semaphore prevents all N semaphores from being decremented by the first call to sem_wait() . As such, there must be at least one semaphore that can be decremented by the second call, guaranteeing one thread enters the critical section. Once that thread leaves, it increments its fork semaphores and the new semaphore, allowing a new thread to enter.
| /* Code Listing 8.26: Solving dining philosophers with a multiplexing semaphore */ void * philosopher (void * _args) { /* Cast the args as struct with self identifier, semaphores */ struct args *args = (struct args *) _args; int self = args->self; /* unique thread identifier */ int next = (self + 1) % SIZE; sem_wait (args->can_sit); /* multiplexing semaphore */ sem_wait (args->sems[self]); /* pick up left fork */ sem_wait (args->sems[next]); /* pick up right fork */ sem_post (args->can_sit); /* multiplexing semaphore */ /* Critical section (eating) */ sem_post (args->sems[next]); /* put down right fork */ sem_post (args->sems[self]); /* put down left fork */ /* Do other work and exit thread */ } |
Example 8.5.2
At first glance, it may appear that placing the call to sem_post() before the critical section could still allow the same problem as before. Specifically, this structure allows N calls to sem_wait() , just as the original version did. However, the order of the outcomes is different, as highlighted in Table 8.2 . If thread 1 was initially blocked by the multiplexing semaphore, thread 0 is able to call sem_wait(1) successfully first. This order of events breaks the circular wait.
| Thread 0 | Thread 1 | Thread 2 | Thread 3 | Thread 4 |
|---|---|---|---|---|
| sem_wait(0); SUCCESS sem_wait(1); | sem_wait(1); | sem_wait(2); SUCCESS sem_wait(3); BLOCKED | sem_wait(3); SUCCESS sem_wait(4); BLOCKED | sem_wait(4); SUCCESS sem_wait(3); BLOCKED |
Table 8.2: The multiplexing semaphore changes where threads get blocked
8.5.2. Solution by Breaking Hold-and-wait ¶
There are times where the previous approach would not be optimal, particularly if there is a large gap between the two calls to sem_wait() in the initial approach. For instance, if we consider the scenario described in Code Listing 8.25 , the threads might retrieve a large amount of data from their incoming port before locking an outgoing port. The multiplexing approach would reduce the number of threads that can perform this initial work until at least one gets past the second semaphore. Depending on the needs of the specific application, this delay may be undesirable.
Code Listing 8.27 outlines a different approach focused on breaking the hold-and-wait criterion. Rather than using sem_wait() on the second semaphore, sem_try_wait() provides a mechanism to detect the failure without blocking. If the semaphore is successfully decremented, the thread continues as normal. However, if the decrement would cause the thread to block, it posts to the first semaphore and starts over from scratch. In the terms of the dining philosopher scenario, if someone fails to grab their right fork they would put their left fork back down and try again. In the meantime, the philosopher to their left could grab the fork before it is picked back up.
| /* Code Listing 8.27: Solving dining philosophers with a multiplexing semaphore */ while (! success) { sem_wait (args->sems[self]); /* pick up left fork */ /* perform some initial work */ if (sem_try_wait (args->sems[next]) != 0) { /* undo current progress if needed and possible */ sem_post (args->sems[self]); /* drop left fork */ } else success = true; } |
This approach depends on the work that is done between waiting on the two semaphores. If the initial work cannot be undone, it is not clear what should be done if the sem_try_wait() fails. One possibility would be simply to discard the partial results, which may be acceptable in some cases. As an example of where this is true, consider a streaming media player. Partial results can happen when some but not all of the data packets have arrived; the result may be that the player switches to a low-resolution form (creating pixelated images) or switches to audio only.
On the other hand, consider a financial database where the initial work is to withdraw money from one account. After waiting on the second semaphore (if successful), the money would be deposited in a second account. However, if the sem_try_wait() fails and the withdraw cannot be undone, the money would be lost. This is clearly not an acceptable result. As such, this approach should be used only in cases where it is clear that the initial work can be undone or discarded safely.
8.5.3. Solution by Imposing Order ¶
A third possibility for solving the dining philosophers problem is to impose a linear ordering on the semaphores. This order could be imposed by requiring i < j anytime sems[i] is accessed before sems[j] . As before, thread 0 would wait on semaphores 0 and 1 (in that order), thread 1 would wait on semaphores 1 and 2, and so on. However, the last thread would have a different ordering. If there are N semaphores (numbered 0 through N-1), the last thread would have to wait on semaphore 0 before semaphore N-1 to adhere to the linear ordering. Code Listing 8.28 shows how this order can be imposed by adding a single if statement.
| /* Code Listing 8.28: Enforcing a linear ordering by requiring self < next */ void * philosopher (void * _args) { /* Cast the args as struct with self identifier, semaphores */ struct args *args = (struct args *) _args; int self = args->self; /* unique thread identifier */ int next = (self + 1) % SIZE; if (self > next) swap (&next, &self); /* enforce order */ sem_wait (args->sems[self]); /* pick up left fork */ sem_wait (args->sems[next]); /* pick up right fork */ /* Critical section (eating) */ sem_post (args->sems[next]); /* put down right fork */ sem_post (args->sems[self]); /* put down left fork */ /* Do other work and exit thread */ } |
Example 8.5.3
To visualize how this change affects the outcomes to prevent deadlock, consider the highlights in Table 8.3 . Since thread 4 must adhere to the linear order, it must try to wait on semaphore 0 before it can wait on semaphore 4. Assuming thread 0 arrived earlier and decremented semaphore 0 successfully as shown, thread 4 becomes blocked from the start. Consequently, thread 3 is successful in decrementing semaphore 4. The linear ordering prevents the circular wait that would cause deadlock.
| Thread 0 | Thread 1 | Thread 2 | Thread 3 | Thread 4 |
|---|---|---|---|---|
| sem_wait(0); SUCCESS sem_wait(1); BLOCKED | sem_wait(1); SUCCESS sem_wait(2); BLOCKED | sem_wait(2); SUCCESS sem_wait(3); BLOCKED | sem_wait(3); SUCCESS sem_wait(4); | sem_wait(0); sem_wait(4); |
Table 8.3: Thread 4 gets blocked by semaphore 0, allowing thread 3 to proceed
The Dining Philosophers
Last updated: November 4, 2022
1. Overview
In this tutorial, we’ll discuss one of the famous problems in concurrent programming – the dining philosophers – formulated by Edgar Dijkstra in 1965. He presented the problem as a demonstration of the problem of resource contention. It occurs when computers need to access shared resources.
2. The Problem Definition
We can see the setup for the problem in the figure below. As we’ve seen, five philosophers are sitting around the table. They live in a house together. There are also five forks on the table between each philosopher.
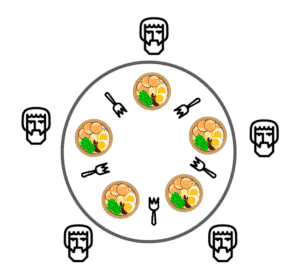
When they think they don’t need any forks. However, assuming the complexity of their food, they have to use two forks, both the one on their right and the one on their left, when they eat. The disagreement, or in other words, contention for these forks, makes this problem important in concurrent programming.
3. Characteristics of the Problem
The first solution that comes to mind is locking each fork with a mutex or a binary semaphore . However, even if we guarantee that no two neighbors are eating simultaneously, this solution may lead to deadlock because all the five philosophers can get hungry simultaneously. In this situation, all of them will grab the fork on their left, and from that moment, no one will access the fork on their right. The philosophers are stuck.
Let’s summarize the other specific characteristics of the problem:
- As we’ve said, a philosopher will need left and right forks to eat food
- Only one philosopher can hold each fork at a certain period, and so a philosopher can use the fork only if another philosopher is not using it
- Philosophers need to put down forks after they finish eating so that forks become available for others
- Also, a philosopher can only get the fork on their right and the one on their left if they are available
- Philosophers cannot start eating before getting both forks
- The problem assumes that there is endless supply and demand so that there is no limit to how much food or stomach space can exist
4. Solution
Of course, there is more than one solution to this problem, but we’re going to look at the original one, which is based on Dijkstra’s solution and changed by Tanenbaum . We’ll share the critic functions in the pseudocode format.
This solution uses one mutex, one semaphore per philosopher, and one state variable per philosopher, which we explained in the previous section.
We have a state array to keep track of every philosopher’s state, whether they’re hungry or not. Also, there are other constant variables to simulate the dining philosophers problem:
As mentioned earlier, we have one mutex to make thread-safe our critical sections, which are our forks and states of philosophers for this problem. And one semaphore for each philosopher:
4.1. Preventing the Deadlock
At this point, we need to carefully decide whether a philosopher is able to eat or not. To do that, imagine we have a waiter who is responsible for telling the philosophers whether they can eat now or they should wait:
For example, philosopher 1 is hungry and starts eating before all of them. And then, philosopher 2 will ask the waiter whether she is allowed to eat or not. The waiter says go and check. She tries to take forks first. However, since both forks are not available, she’ll need to wait.
After philosopher 1 finishes eating, we call the put_forks() and the check() functions to make available the forks for other philosophers:
The check () functions inside take_forks() and put_forks() functions will prevent the deadlock.
Finally, let’s look at the eat() and think() methods that our philosophers enjoy doing during their lifetime:
These two functions just print the information about which philosopher thinks or eats. It also puts the philosopher threads to sleep at random duration:
5. What Can Be Wrong?
We’ve already discussed that we can have a deadlock situation when we don’t adjust the necessary synchronization primitives.
Starvation is another issue that we need to consider when developing concurrent programs. Resource starvation may happen if any philosopher cannot take both forks because of a timing problem.
These problems can occur when multiple processes need access to shared resources. These topics generally are studies in concurrent programming. Dijkstra did a great job of coming up with a problem analogous to such difficulties in real computer systems.
6. Conclusion
In this article, we’ve given the description and the solution to the dining philosophers. It’s analogous to resource contention problems in computing systems and proposed by the Dijkstra. We’ve also discussed the important synchronization problems such as deadlock and how to prevent it in the scope of the dining philosophers.
Furthermore, we can check the Java implementation of the dining philosophers problem .
Dining Philosophers Problem in OS
Dining Philosophers Problem in OS is a classical synchronization problem in the operating system. With the presence of more than one process and limited resources in the system the synchronization problem arises. If one resource is shared between more than one process at the same time then it can lead to data inconsistency.
Consider two processes P1 and P2 executing simultaneously, while trying to access the same resource R1 , this raises the question of who will get the resource and when. This problem is solved using process synchronization.
The act of synchronizing process execution such that no two processes have access to the same associated data and resources are referred to as process synchronization in operating systems.
It's particularly critical in a multi-process system where multiple processes are executing at the same time and trying to access the very same shared resource or data.
This could lead to discrepancies in data sharing. As a result, modifications implemented by one process may or may not be reflected when the other processes access the same shared data. The processes must be synchronized with one another to avoid data inconsistency.
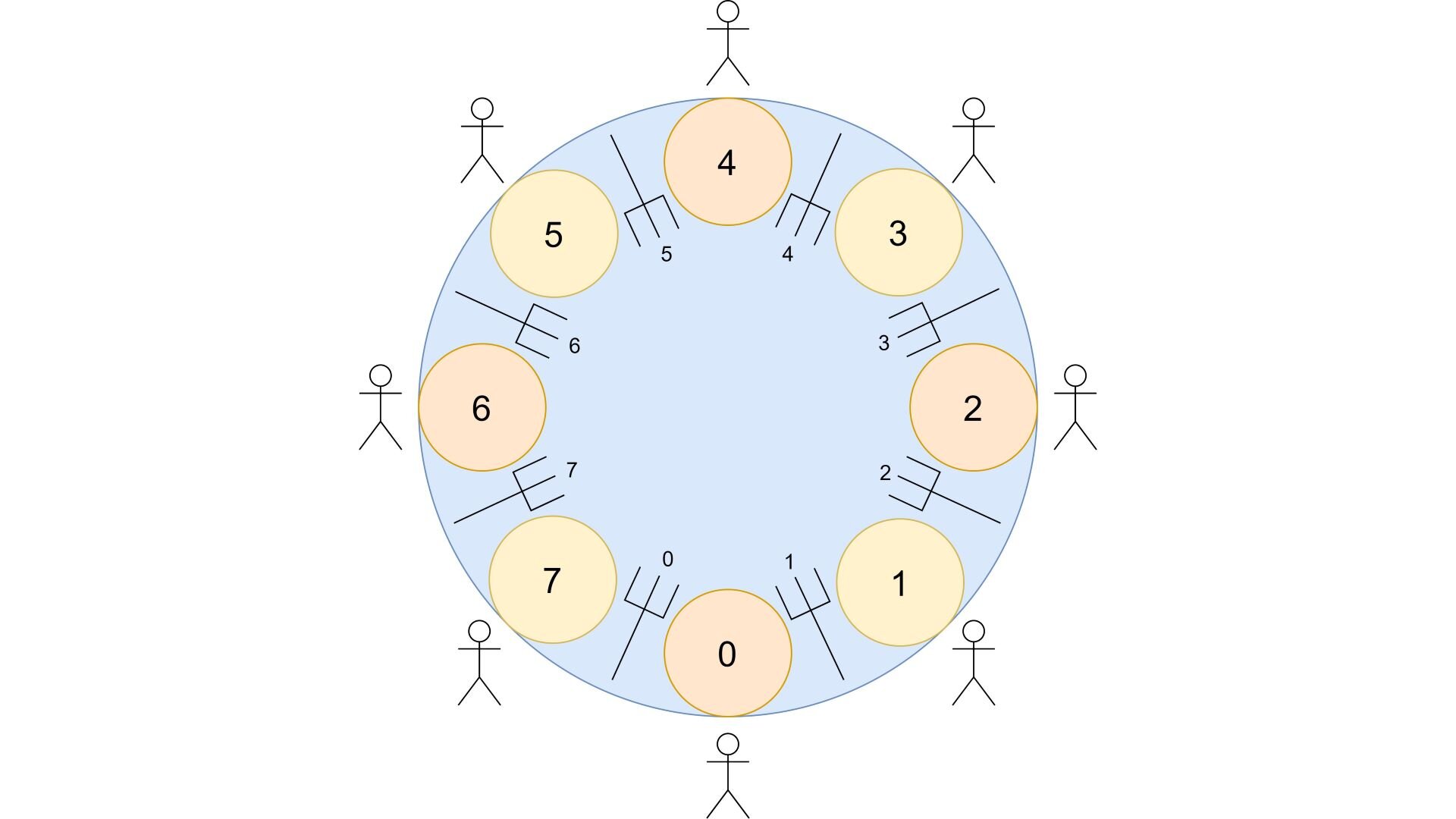
And the Dining Philosophers Problem is a typical example of limitations in process synchronization in systems with multiple processes and limited resources. According to the Dining Philosopher Problem , assume there are K philosophers seated around a circular table, each with one chopstick between them. This means, that a philosopher can eat only if he/she can pick up both chopsticks next to him/her. One of the adjacent followers may take up one of the chopsticks, but not both.
For example, let’s consider P0 , P1 , P2 , P3 , and P4 as the philosophers or processes and C0 , C1 , C2 , C3 , and C4 as the 5 chopsticks or resources between each philosopher. Now if P0 wants to eat, both resources/chopsticks C0 and C1 must be free, which would leave P1 and P4 void of the resource and the process wouldn't be executed, which indicates there are limited resources( C0 , C1 ..) for multiple processes( P0 , P1 ..), and this problem is known as the Dining Philosopher Problem .
The Solution of the Dining Philosophers Problem
The solution to the process synchronization problem is Semaphores , A semaphore is an integer used in solving critical sections.
The critical section is a segment of the program that allows you to access the shared variables or resources. In a critical section, an atomic action (independently running process) is needed, which means that only a single process can run in that section at a time.
Semaphore has 2 atomic operations: wait() and signal() . If the value of its input S is positive, the wait() operation decrements, it is used to acquire resources while entry. No operation is done if S is negative or zero. The value of the signal() operation's parameter S is increased, it is used to release the resource once the critical section is executed at exit.
Here's a simple explanation of the solution:
Explanation:
- The wait() operation is implemented when the philosopher is using the resources while the others are thinking. Here, the threads use_resource[x] and use_resource[(x + 1) % 5] are being executed.
- After using the resource, the signal() operation signifies the philosopher using no resources and thinking. Here, the threads free_resource[x] and free_resource[(x + 1) % 5] are being executed.
To model the Dining Philosophers Problem in a C program we will create an array of philosophers (processes) and an array of chopsticks (resources). We will initialize the array of chopsticks with locks to ensure mutual exclusion is satisfied inside the critical section.
We will run the array of philosophers in parallel to execute the critical section (dine ()) , the critical section consists of thinking, acquiring two chopsticks, eating and then releasing the chopsticks.
Let's Understand How the Above Code is Giving a Solution to the Dining Philosopher Problem?
We start by importing the libraries pthread for threads and semaphore for synchronization. And create an array of 5 p_threads representing the philosophers. Create an array of 5 mutexes representing the chopsticks.
The pthread library is used for multi-threaded programming which allows us to run parallel sub-routines using threads. The <semaphore.h> header is used to perform semaphore operations.
We initialise the counter i and status message variable as int and a pointer msg, and intialise the semaphore array.
We create the philosopher threads using pthread_create and pass a pointer to the dine function as the subroutine and a pointer to the counter variable i .
All the philosophers start by thinking. We pass chopstick(n) (left) to pthread_mutex_lock to wait and acquire lock on it.
Then the thread waits on the right((n+1) % NUM_CHOPSTICKS) chopstick to acquire a lock on it (pick it up).
When the philosopher successfully acquires lock on both the chopsticks, the philosopher starts dining (sleep(3)).
Once the philosopher finishes eating, we call pthread_mutex_unlock on the left chopstick (signal) thereby freeing the lock. Then proceed to do the same on the right chopstick.
We loop through all philosopher threads and call pthread_join to wait for the threads to finish executing before exiting the main thread.
We loop thorough the chopstick array and call pthread_mutex_destroy to destroy the semaphore array.
The Drawback of the Above Solution of the Dining Philosopher Problem
Through the above discussion, we established that no two nearby philosophers can eat at the same time using the aforementioned solution to the dining philosopher problem. The disadvantage of the above technique is that it may result in a deadlock situation. This occurs when all of the philosophers choose their left chopstick at the same moment, resulting in a stalemate scenario in which none of the philosophers can eat, and hence deadlock will happen.
We can also avoid deadlock through the following methods in this scenario -
The maximum number of philosophers at the table should not exceed four, let’s understand why four processes is important:
- Chopstick C4 will be accessible for philosopher P3 , therefore P3 will begin eating and then set down both chopsticks C3 and C4 , indicating that semaphore C3 and C4 will now be increased to one.
- Now that philosopher P2 , who was holding chopstick C2 , also has chopstick C3 , he will place his chopstick down after eating to allow other philosophers to eat.
The four starting philosophers (P0, P1, P2, and P3) must pick the left chopstick first, then maybe the right, even though the last philosopher ( P4 ) should pick the right chopstick first, then the left. Let's have a look at what occurs in this scenario:
- This will compel P4 to hold his right chopstick first since his right chopstick is C0 , which is already held by philosopher P0 and whose value is set to 0 , i.e. C0 is already 0 , trapping P4 in an unending loop and leaving chopstick C4 empty.
- As a result, because philosopher P3 has both left C3 and right C4 chopsticks, it will begin eating and then put down both chopsticks once finished, allowing others to eat, thereby ending the impasse.
If the philosopher is in an even position, he/she should choose the right chopstick first, followed by the left, and in an odd position, the left chopstick should be chosen first, followed by the right.
Only if both chopsticks (left and right) are accessible at the same time should a philosopher be permitted to choose his or her chopsticks.
Unlock the secrets of operating systems with our Operating System free course. Enroll now to get a comprehensive overview of their role and functionalities.
- Process synchronization is defined as no two processes have access to the same associated data and resources.
- The Dining philosopher problem is an example of a process synchronization problem.
- Philosopher is an analogy for process and chopstick for resources, we can try to solve process synchronization problems using this.
- The solution of the Dining Philosopher problem focuses on the use of semaphores.
- No two nearby philosophers can eat at the same time using the aforesaid solution to the dining philosopher problem, and this situation causes a deadlock, this is a drawback of the Dining philosopher problem.
- [email protected]

What’s New ?
The Top 10 favtutor Features You Might Have Overlooked

- Don’t have an account Yet? Sign Up
Remember me Forgot your password?
- Already have an Account? Sign In
Lost your password? Please enter your email address. You will receive a link to create a new password.
Back to log-in
By Signing up for Favtutor, you agree to our Terms of Service & Privacy Policy.
Dining Philosophers Problem using Semaphores (with Solution)
- May 30, 2023
- 6 Minute Read
- Why Trust Us We uphold a strict editorial policy that emphasizes factual accuracy, relevance, and impartiality. Our content is crafted by top technical writers with deep knowledge in the fields of computer science and data science, ensuring each piece is meticulously reviewed by a team of seasoned editors to guarantee compliance with the highest standards in educational content creation and publishing.
- By Harshita Rajput

Let's learn about an interesting problem of operating systems today. Dining Philosopher's Problem originated from the field of concurrent programming when multiple processes contend for limited resources while also avoiding deadlock.
Dining Philosopher's Problem Statement
This is a classic synchronization problem in computer science that demonstrates the challenges of resource allocation and concurrency.
We have been provided with a table where 5 philosophers are sitting for dining. In the middle of the table, noodles have been kept and we have 5 plates and 5 forks. It is given that either the philosophers will be in an eating state or a thinking state. To eat the noodles, each philosopher needs 2 forks and picks the forks one by one.
This implies we need 10 forks as per their need. So how do we synchronize their actions so that we are able to create a system where whichever philosopher is about to eat, gets the 2 forks and we get a deadlock-free system?
From the problem statement, we know it is a critical section problem. As 'fork' here can be treated as a shared variable between 2 philosophers or processes. And just like a classical critical section problem, here we need to synchronize in such a way that till a philosopher says, p1 is not done with eating, another philosopher says p2, does not disturb p1.
The Dining Philosophers Problem serves as an abstract representation of real-world challenges like highlighting the need for synchronization techniques to ensure the fair allocation of resources and prevent deadlock.
To solve this critical section problem, we use an integer value called semaphore.
Approach to Solution
Here is the simple approach to solving it:
- We convert each fork as a binary semaphore. That implies there exists an array of semaphore data types of forks having size = 5. It initially contains 1 at all positions.
- Now when a philosopher picks up a fork he calls wait() on fork[i] which means that i'th philosopher has acquired the fork.
- If a philosopher has done eating he calls release(). That implies fork[i] is released and any other philosopher can pick up this fork and can start eating.
Here is the code for this approach:
How does this solution work?
The i-th philosopher will pick i-th fork and fork kept at (i + 1) % 5 positions. As the table is circular and if we take i = 5, the philosopher will pick the 5th fork but to pick the second correct fork, we used (i + 1) % 5.
If i = 1, we call one by one wait function due to which the philosopher picks up the 1st and 2nd fork. After he has finished eating, he releases the fork and starts thinking, and this is how we are ensuring that no two adjacent philosophers eat simultaneously.
Now as we saw, this solution is ensuring that the neighbors say p1 and p2 are not eating simultaneously but this doesn't ensure that we will not witness a situation of deadlock.
Let's see how we can get the deadlock situation.
Assume all the philosophers have picked their leftmost fork. Now there arises a deadlock condition as here, each philosopher is waiting for their rightmost fork to be free. Only if p5 leaves its fork, p1 can have the food, and p5 will only leave its fork if p4 gives him the fork. So this creates an infinite loop and hence a deadlock situation.
Approach to solving this deadlock condition
Here is the approach to solving Dining Philosopher's Problem in this deadlock condition:
- If we allow at most 4 philosophers to be sitting simultaneously. After doing so at least one of the philosophers can go to the eating stage and hence other philosophers can after he releases the fork.
- Allow the philosopher to pick his fork only and only if both forks are available. So to implement this, we convert the wait() calls into a critical section and so we introduce a new lock. This lock will ensure that the philosopher gets both forks at once.
- Odd-Even rule: We can identify the philosophers by their position if it is even or odd. All the philosophers at odd positions pick the fork kept at their left and then the fork at their right. The philosophers at even position can pick the fork at the right position and then the fork at their left.
Conclusion
The dining philosophers is a classic problem related to synchronization. In the operating system, we assume the philosophers to be processed and forks as the resources. The same technique is used in operating systems too and this way we avoid the deadlock situation.

FavTutor - 24x7 Live Coding Help from Expert Tutors!

About The Author

Harshita Rajput
More by favtutor blogs, monte carlo simulations in r (with examples), aarthi juryala.

The unlist() Function in R (with Examples)

Paired Sample T-Test using R (with Examples)


Operating System
- Interview Q
Process Management
Synchronization, memory management, file management.
| The dining philosopher's problem is the classical problem of synchronization which says that Five philosophers are sitting around a circular table and their job is to think and eat alternatively. A bowl of noodles is placed at the center of the table along with five chopsticks for each of the philosophers. To eat a philosopher needs both their right and a left chopstick. A philosopher can only eat if both immediate left and right chopsticks of the philosopher is available. In case if both immediate left and right chopsticks of the philosopher are not available then the philosopher puts down their (either left or right) chopstick and starts thinking again. The dining philosopher demonstrates a large class of concurrency control problems hence it's a classic synchronization problem. - Let's understand the Dining Philosophers Problem with the below code, we have used fig 1 as a reference to make you understand the problem exactly. The five Philosophers are represented as P0, P1, P2, P3, and P4 and five chopsticks by C0, C1, C2, C3, and C4. Let's discuss the above code: Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute by doing this it holds after that it execute by doing this it holds ( since i =0, therefore (0 + 1) % 5 = 1) Similarly suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute by doing this it holds after that it execute by doing this it holds ( since i =1, therefore (1 + 1) % 5 = 2) But Practically Chopstick C1 is not available as it has already been taken by philosopher P0, hence the above code generates problems and produces race condition. We use a semaphore to represent a chopstick and this truly acts as a solution of the Dining Philosophers Problem. Wait and Signal operations will be used for the solution of the Dining Philosophers Problem, for picking a chopstick wait operation can be executed while for releasing a chopstick signal semaphore can be executed. Semaphore: A semaphore is an integer variable in S, that apart from initialization is accessed by only two standard atomic operations - wait and signal, whose definitions are as follows: From the above definitions of wait, it is clear that if the value of S <= 0 then it will enter into an infinite loop(because of the semicolon; after while loop). Whereas the job of the signal is to increment the value of S. The structure of the chopstick is an array of a semaphore which is represented as shown below - Initially, each element of the semaphore C0, C1, C2, C3, and C4 are initialized to 1 as the chopsticks are on the table and not picked up by any of the philosophers. Let's modify the above code of the Dining Philosopher Problem by using semaphore operations wait and signal, the desired code looks like In the above code, first wait operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows philosopher i have picked up the chopsticks from its left and right. The eating function is performed after that. On completion of eating by philosopher i the, signal operation is performed on take_chopstickC[i] and take_chopstickC [ (i+1) % 5]. This shows that the philosopher i have eaten and put down both the left and right chopsticks. Finally, the philosopher starts thinking again. Let value of i = 0( initial value ), Suppose Philosopher P0 wants to eat, it will enter in Philosopher() function, and execute by doing this it holds and reduces semaphore C0 to 0 after that it execute by doing this it holds ( since i =0, therefore (0 + 1) % 5 = 1) and reduces semaphore C1 to 0 Similarly, suppose now Philosopher P1 wants to eat, it will enter in Philosopher() function, and execute by doing this it will try to hold but will not be able to do that since the value of semaphore C1 has already been set to 0 by philosopher P0, therefore it will enter into an infinite loop because of which philosopher P1 will not be able to pick chopstick C1 whereas if Philosopher P2 wants to eat, it will enter in Philosopher() function, and execute by doing this it holds and reduces semaphore C2 to 0, after that, it executes by doing this it holds ( since i =2, therefore (2 + 1) % 5 = 3) and reduces semaphore C3 to 0. Hence the above code is providing a solution to the dining philosopher problem, A philosopher can only eat if both immediate left and right chopsticks of the philosopher are available else philosopher needs to wait. Also at one go two independent philosophers can eat simultaneously (i.e., philosopher can eat simultaneously as all are the independent processes and they are following the above constraint of dining philosopher problem) From the above solution of the dining philosopher problem, we have proved that no two neighboring philosophers can eat at the same point in time. The drawback of the above solution is that this solution can lead to a deadlock condition. This situation happens if all the philosophers pick their left chopstick at the same time, which leads to the condition of deadlock and none of the philosophers can eat. To avoid deadlock, some of the solutions are as follows - The design of the problem was to illustrate the challenges of avoiding deadlock, a deadlock state of a system is a state in which no progress of system is possible. Consider a proposal where each philosopher is instructed to behave as follows: |

- Send your Feedback to [email protected]
Help Others, Please Share

Learn Latest Tutorials
Transact-SQL
Reinforcement Learning
R Programming
React Native
Python Design Patterns
Python Pillow
Python Turtle
Preparation

Verbal Ability

Interview Questions

Company Questions
Trending Technologies
Artificial Intelligence
Cloud Computing
Data Science
Machine Learning
B.Tech / MCA
Data Structures
Computer Network
Compiler Design
Computer Organization
Discrete Mathematics
Ethical Hacking
Computer Graphics
Software Engineering
Web Technology
Cyber Security
C Programming
Control System
Data Mining
Data Warehouse

Philosophical Problems
Let’s start off easy. A “Philosophical Problem” is like a super tough riddle about life and the universe that even the smartest people can’t quite solve. Imagine you’ve found a strange puzzle box at a garage sale with no instructions. Opening it is tough because you don’t know how it works, yet you have a feeling that you can figure it out. That’s what a philosophical problem is like.
Now, to be more detailed, a philosophical problem is a hard question about life, reality, and what it means to be a good person. It’s not something that can be answered with a calculator or a crazy invention. It’s the kind of question that might keep you awake at night because the answer doesn’t come easily. Philosophers are people who can’t help but wonder about these questions, like why we dream or if there’s a perfect way to live.
Approaching the Problems
So, how do you start figuring out these brain-twisters? Think big! Ask yourself those weird questions. Why is there anything at all? Is there a way to live the best life possible? You don’t need fancy gadgets for this; your brain is your best tool. Talk about it with friends or someone who loves to think deeply about things. Read books by people who have been thinking about these problems for years. and why not try writing your thoughts down? That can really help make things clear.
Types of Philosophical Problems
There are different types of philosophical problems, kind of like different genres of video games. Some you might battle through like an epic adventure, and some are more like puzzles that need solving. Now, imagine all the diverse games out there; philosophical problems are just as varied:
- Metaphysical problems : These are like the mysteries of the universe. They make us wonder about things we can’t see or touch but somehow just know are there.
- Epistemological problems : This is like the maze of knowledge . It’s all about questioning how we learn things and what it means to truly “know” something.
- Ethical problems : Picture a crossroads where each path is a different choice between right and wrong. These are the problems that deal with what we should do or shouldn’t do.
- Logical problems : These are like brain training puzzles. They make us think twice about how we make sense of things and argue our points.
- Aesthetic problems : Imagine standing in an art gallery, wondering why one painting makes you feel happy and another makes you feel sad. These questions are about art and beauty.
- Political philosophy problems : This is like the strategy in a multiplayer game where everyone has to decide on the rules and how to play fair. They focus on law, society, and what being fair means.
This one is a classic head-scratcher because it makes us question everything around us. It’s like questioning if a movie is real life or just a bunch of pictures flashing quickly.
This is about figuring out if we can ever be 100% sure about anything. It’s like trying to find your way around a new town without a map—you’re not always sure you’re going the right way, even if you think you are.
It’s like looking at an intricate toy and wondering who made it and why. We’re part of something much bigger, and it’s strange to think why there’s anything instead of just empty space.
This is all about the mystery of how our brains and bodies work together. It’s like having two teammates in a game who need to work perfectly together, but you’re not quite sure how they communicate.
This question is like wondering if we are the players or just characters in a video game following a script. It’s all about choice and whether we’re really in control of our actions or not.
Why Is Philosophy Important?
Knowing about philosophy is a big deal because it’s like training for your mind. It helps you think more clearly and ask better questions. Whenever you’re trying to figure out the tricky stuff, like what to believe, philosophy gives you the moves to do it. It helps make you a keen idea detective, always ready to learn something new or see things from a different side.
Plus, it’s not just about knowing stuff—it’s about how you live your life. Philosophy encourages you to dig into the real meaning behind everyday things, and that can make your life richer and more interesting. Bottom line, it can help you stand up for what you believe in and be the kind of person you want to be.
Origin of Philosophical Problems
These brain teasers aren’t new. Think of them as vintage, like old vinyl records that are still cool today. Ancient guys like Socrates, Plato , and Aristotle were some of the first to ask these big questions. They set the stage, and since then, people from all over the world and all through history have been adding their own thoughts into the mix.
Controversies in Philosophy
Because these puzzles have no clear answers, people often end up in debates. Philosophers have argued for ages, throwing different ideas back and forth. One big question today is whether philosophy still matters, now that we know so much about the world through science. But many say it’s more important than ever because it helps us handle new challenges and changes in our world.

Why Do Philosophical Problems Persist?
Philosophical problems stick around because they aren’t like a math quiz that has clear answers. They are tied to who we are as people, and they grow and change as we meet new thinkers, discover new things, and as the world changes around us.
Philosophy in Everyday Life
Believe it or not, you’re probably doing philosophy without even realizing it. When you debate with your friends about what’s fair or not, or wonder about the truth of something, you’re being a philosopher. It’s not just a thing for old guys in libraries; it’s for everybody trying to work out life’s big puzzles.
Related Topics
- Existentialism : This is like your personal philosophy story. It’s about your life, the choices you make, and the freedom you have to make those choices. It’s thinking about why things can feel confusing or strange.
- Cognition and Psychology : Even though these are scientific, they mix with philosophy as they investigate how we think, make decisions, and what makes us conscious beings.
- Science and Ethics : This is where science and philosophy hang out. It’s about looking at new inventions and discoveries and asking if they are right or wrong.
- Comparative Religion : Think of this as the study of what people believe and why. It asks about faith, its meaning, and how people find a sense of peace and understanding.
- Philosophy of Science : This takes a step back and looks at science itself, questioning how we come to know things through science, what a scientific theory is, and how we can be sure about scientific facts.
To wrap up, philosophical problems are these big, fascinating riddles about why we’re here, what everything means, and how we fit into the world. They aren’t just puzzles for the pros; they help everyone figure out the mysteries we bump into every day. By thinking about these problems, we train our brains to be sharper thinkers and problem-solvers, and we get better at understanding and connecting with the people and the world around us. No matter what, exploring these questions is part of what makes us curious, smart humans, always looking for answers and new adventures in thinking.
Plato's Problem Solving: Doing the Right Thing

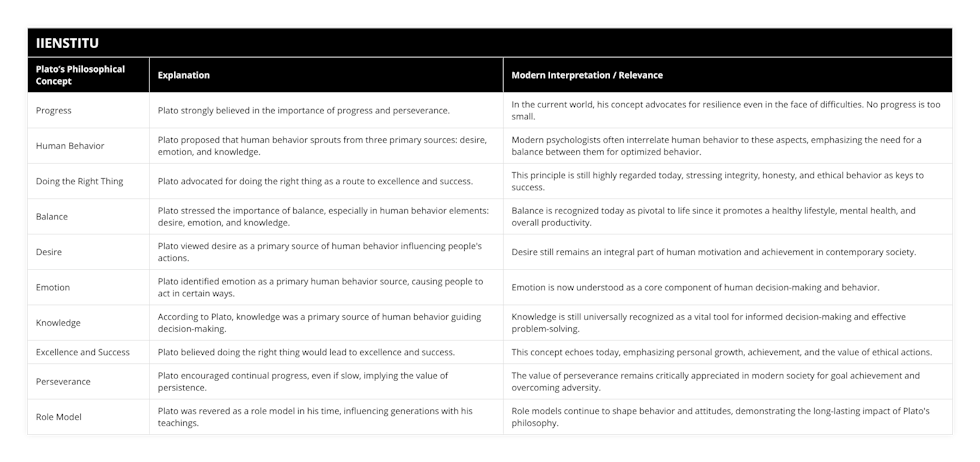
| Plato’s Philosophical Concept | Explanation | Modern Interpretation / Relevance |
|---|---|---|
| Progress | Plato strongly believed in the importance of progress and perseverance. | In the current world, his concept advocates for resilience even in the face of difficulties. No progress is too small. |
| Human Behavior | Plato proposed that human behavior sprouts from three primary sources: desire, emotion, and knowledge. | Modern psychologists often interrelate human behavior to these aspects, emphasizing the need for a balance between them for optimized behavior. |
| Doing the Right Thing | Plato advocated for doing the right thing as a route to excellence and success. | This principle is still highly regarded today, stressing integrity, honesty, and ethical behavior as keys to success. |
| Balance | Plato stressed the importance of balance, especially in human behavior elements: desire, emotion, and knowledge. | Balance is recognized today as pivotal to life since it promotes a healthy lifestyle, mental health, and overall productivity. |
| Desire | Plato viewed desire as a primary source of human behavior influencing people's actions. | Desire still remains an integral part of human motivation and achievement in contemporary society. |
| Emotion | Plato identified emotion as a primary human behavior source, causing people to act in certain ways. | Emotion is now understood as a core component of human decision-making and behavior. |
| Knowledge | According to Plato, knowledge was a primary source of human behavior guiding decision-making. | Knowledge is still universally recognized as a vital tool for informed decision-making and effective problem-solving. |
| Excellence and Success | Plato believed doing the right thing would lead to excellence and success. | This concept echoes today, emphasizing personal growth, achievement, and the value of ethical actions. |
| Perseverance | Plato encouraged continual progress, even if slow, implying the value of persistence. | The value of perseverance remains critically appreciated in modern society for goal achievement and overcoming adversity. |
| Role Model | Plato was revered as a role model in his time, influencing generations with his teachings. | Role models continue to shape behavior and attitudes, demonstrating the long-lasting impact of Plato's philosophy. |
Plato was an influential ancient philosopher born in 428/427 BC in Athens. He advocated for progress and believed that human behavior resulted from three primary sources: desire, emotion, and knowledge. He also thought one could achieve excellence and success by doing the right thing. His teachings have been remembered and respected for centuries and continue to be a source of inspiration for many today.
Introduction
Plato's Quote on Progress
Plato's View on Human Behavior
Plato's pursuit of doing the right thing.
Introduction: Plato was one of the ancient world's most influential and vital philosophers. He was born in 428/427 BC in and around Athens and studied under the renowned philosopher Socrates. Plato devoted his life to philosophy, science, and religion and is remembered for his thought-provoking and often controversial ideas. One of Plato's most famous quotes is, "Don't discourage anyone who continually makes progress, no matter how slowly." This quote is a testament to his belief in the importance of perseverance and progress. It also reflects his view that moving forward is always the correct answer, even when faced with challenges.
Plato also had a unique view of human behavior. He believed human behavior resulted from three primary sources: desire, emotion, and knowledge. He argued that these three sources were the driving forces behind human behavior and had to be balanced to achieve the desired outcome. This view was somewhat surprising, as it was not the prevailing view of the time. Nevertheless, many modern thinkers and psychologists have since adopted Plato's ideas on human behavior.
Plato was also known for his pursuit of doing the right thing. He believed that one could achieve excellence and success by doing the right thing. He was a role model for his time; even today, his teachings are remembered and respected. Plato argued that by doing the right thing, one could create a better future for oneself and society.
Conclusion: Plato was a great thinker and philosopher with a unique worldview. He believed that progress was essential and that human behavior resulted from three primary sources. He also argued that one could achieve excellence and success by doing the right thing. Plato's teachings have been remembered and respected for centuries and continue to be a source of inspiration for many today. His problem-solving skills and pursuit of doing the right thing have been an example for generations.
The path to success begins with understanding the right thing to do. - Plato IIENSTITU
What was Plato's view on human behavior?
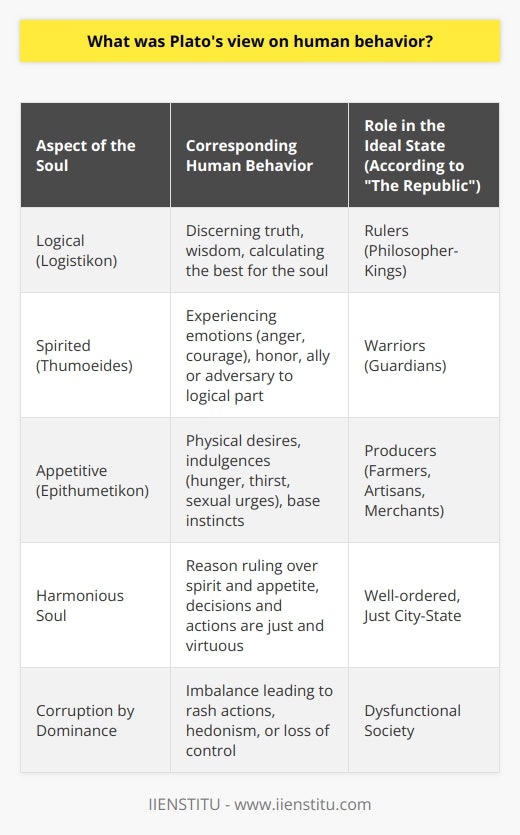
Plato, a Classical Greek philosopher, was renowned for his works on human behavior. He believed the soul was composed of three parts: reason, spirit, and appetite. He argued that reason should be the dominant part of the soul and be used to control the mood and appetite. He argued that a person’s soul determines human behavior and should be directed by reason instead of spirit or appetite.
Plato believed that humans should strive to achieve a state of harmony and balance between the three components of the soul. He argued that when the three components of the soul are in harmony, a person can live a virtuous and just life. He argued that virtue and justice are essential to a prosperous and harmonious life and can only be achieved when reason is the dominant component of the soul.
Plato argued that when reason dominates the soul, people can make decisions that align with their true identity. He argued that when people are guided by their defense, they can make decisions based on their values and beliefs. He believed that when a person is guided by their reason, they will be able to achieve a state of harmony and balance in their life. Plato argued that the reason behind human behavior is the soul. He argued that the soul is the source of the human condition and that it should be used to guide behavior. He argued that when reason is the dominant component of the soul, humans can make decisions consistent with their true identity. He argued that when reason is the chief component of the soul, humans can achieve a state of harmony and balance in their life.
How did Plato's pursuit of doing the right thing lead to achievement and excellence?
The Ancient Greek philosopher Plato is widely remembered for his influential works on politics, ethics, and philosophy. He is credited with establishing the foundations of Western philosophy, and his writings have been studied for centuries. This blog post will explore how Plato’s pursuit of doing the right thing led to achievement and excellence.
Plato was a firm believer in the idea that morality and justice should be the guiding principles for human behavior. He argued that pursuing the right thing was the only way to achieve excellence and success. According to Plato, true excellence could only be attained through justice and virtue. He argued that it was wrong to pursue pleasure or wealth as the end goal, as these would lead to corruption and immorality.
In his works, Plato wrote extensively about justice and virtue. He argued that justice should be the foundation of all societies and the key to achieving excellence. He believed that justice should be based on the principle of fairness and that it should be applied equally to all members of society. He argued that it was wrong to pursue wealth or power without considering its effects on others.
Plato also held that excellence was achievable through the pursuit of knowledge and wisdom. He argued that knowledge was the key to achieving excellence and that it was necessary to seek knowledge and understanding to achieve one’s potential. He also believed that knowledge was essential to making wise decisions.
Finally, Plato believed that excellence could be achieved through the pursuit of virtue. He argued that it was necessary to strive for excellence in all areas of life, including one’s moral character. He argued that integrity was essential for achieving excellence, allowing one to make wise decisions, act with justice, and strive for greatness.
In conclusion, Plato’s pursuit of doing the right thing led to achievement and excellence. He argued that justice, knowledge, and virtue were the foundations of transcendence and that one could achieve greatness only through pursuing these principles. His works continue to be studied and praised centuries later, and his ideas remain relevant today.

What is the significance of Plato's quote on progress?
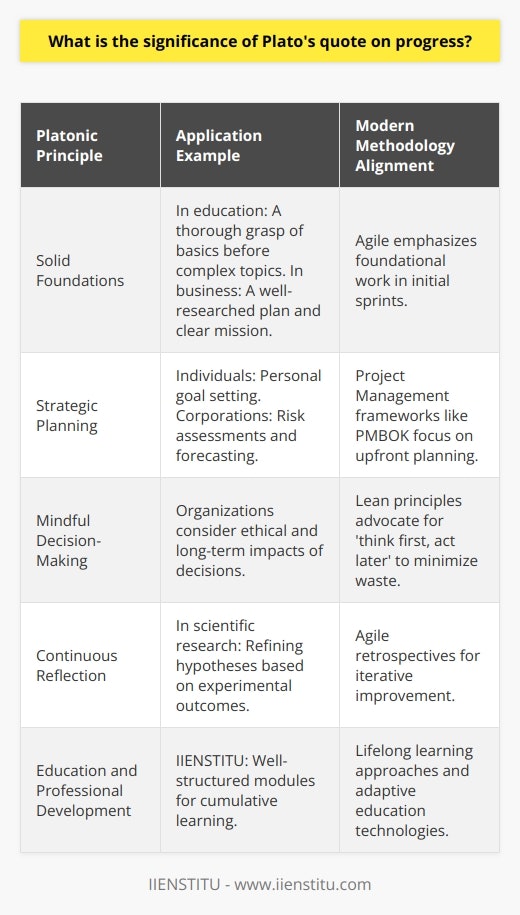
Plato's quote, "The beginning is the most important part of the work," is one of the most well-known philosophical sayings. It speaks to the importance of planning and foresight, and the implications of this quote for progress are significant.
Firstly, PPlato'squote emphasizes the need for a strong foundation. To achieve any progress, it is essential to have a solid starting point, or the project or goal may quickly unravel. Furthermore, a solid foundation allows for the proper evaluation of risks and the development of strategies, which will help to ensure the progress is sustainable.
Secondly, Plato's quote encouragesPlato'sctive an approach to progress. By planning and preparing, it is possible to anticipate obstacles and come up with creative solutions. This proactive approach can help to ensure that progress is made efficiently and effectively.
Thirdly, Plato's quote highlights the importance of makinPlato'shtful decisions. Too often, progress is made without much consideration for the consequences, leading to short-term gains with long-term losses. Taking the time to think through the implications of decisions can help to ensure that progress is meaningful and beneficial in the long run.
Finally, Plato's quote encourages reflection. Progress is Plato'sinear process, and it is essential to take the time to reflect on successes, failures, and lessons learned. Such a review can help identify further improvement opportunities and ensure that progress is meaningful and sustainable.
In summary, Plato's quote on progress has great significance. Plato'sg foundation, a proactive approach, thoughtful decisions, and reflection are all essential components of progress. Considering these elements makes it possible to create meaningful and sustainable progress.
Yu Payne is an American professional who believes in personal growth. After studying The Art & Science of Transformational from Erickson College, she continuously seeks out new trainings to improve herself. She has been producing content for the IIENSTITU Blog since 2021. Her work has been featured on various platforms, including but not limited to: ThriveGlobal, TinyBuddha, and Addicted2Success. Yu aspires to help others reach their full potential and live their best lives.

What are Problem Solving Skills?

3 Apps To Help Improve Problem Solving Skills

How To Improve Your Problem-Solving Skills

Improve Your Critical Thinking and Problem Solving Skills

7 Problem Solving Skills You Need to Succeed

Edison's 99%: Problem Solving Skills

How To Become a Great Problem Solver?

A Problem Solving Method: Brainstorming
- Engineering Mathematics
- Discrete Mathematics
- Operating System
- Computer Networks
- Digital Logic and Design
- C Programming
- Data Structures
- Theory of Computation
- Compiler Design
- Computer Org and Architecture
Dining-Philosophers Solution Using Monitors
Prerequisite: Monitor , Process Synchronization
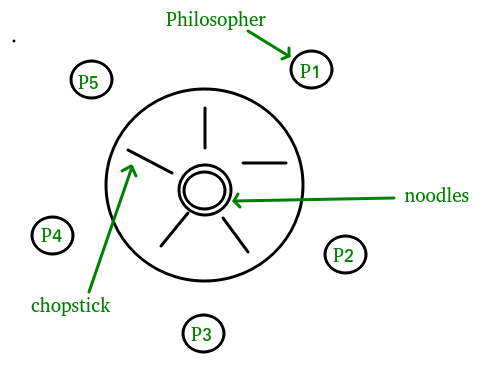
- There is one chopstick between each philosopher
- A philosopher must pick up its two nearest chopsticks in order to eat
- A philosopher must pick up first one chopstick, then the second one, not both at once
We need an algorithm for allocating these limited resources(chopsticks) among several processes(philosophers) such that solution is free from deadlock and free from starvation. There exist some algorithm to solve Dining – Philosopher Problem, but they may have deadlock situation. Also, a deadlock-free solution is not necessarily starvation-free. Semaphores can result in deadlock due to programming errors. Monitors alone are not sufficiency to solve this, we need monitors with condition variables Monitor-based Solution to Dining Philosophers We illustrate monitor concepts by presenting a deadlock-free solution to the dining-philosophers problem. Monitor is used to control access to state variables and condition variables. It only tells when to enter and exit the segment. This solution imposes the restriction that a philosopher may pick up her chopsticks only if both of them are available. To code this solution, we need to distinguish among three states in which we may find a philosopher. For this purpose, we introduce the following data structure: THINKING – When philosopher doesn’t want to gain access to either fork. HUNGRY – When philosopher wants to enter the critical section. EATING – When philosopher has got both the forks, i.e., he has entered the section. Philosopher i can set the variable state[i] = EATING only if her two neighbors are not eating (state[(i+4) % 5] != EATING) and (state[(i+1) % 5] != EATING).
Above Program is a monitor solution to the dining-philosopher problem. We also need to declare
This allows philosopher i to delay herself when she is hungry but is unable to obtain the chopsticks she needs. We are now in a position to describe our solution to the dining-philosophers problem. The distribution of the chopsticks is controlled by the monitor Dining Philosophers. Each philosopher, before starting to eat, must invoke the operation pickup(). This act may result in the suspension of the philosopher process. After the successful completion of the operation, the philosopher may eat. Following this, the philosopher invokes the putdown() operation. Thus, philosopher i must invoke the operations pickup() and putdown() in the following sequence:
It is easy to show that this solution ensures that no two neighbors are eating simultaneously and that no deadlocks will occur. We note, however, that it is possible for a philosopher to starve to death.
When will the Deadlock occur?
Deadlock occurs when two or more processes are blocked, waiting for each other to release a resource that they need. This can happen in solutions that allow a philosopher to pick up one chopstick at a time, or that allow all philosophers to pick up their left chopstick simultaneously.
When will Starvation occur?
Starvation occurs when a process is blocked indefinitely from accessing a resource that it needs. This can happen in solutions that give priority to certain philosophers or that allow some philosophers to continually acquire the chopsticks while others are unable to.
Please Login to comment...
Similar reads.
- Operating Systems
Improve your Coding Skills with Practice
What kind of Experience do you want to share?
Philosophers' Thinking (Heuristics and Problem-Solving (Volume 2)
Philosophers' Thinking (Heuristics and Problem-Solving (Volume 2), 2017
182 Pages Posted: 14 Apr 2017
Ulrich de Balbian
Meta-Philosophy Research Cente; Meta-Philosophy Research Center
Date Written: April 13, 2017
This section or chapter two. Because of its length I decided to create a second Volume 2. HEURISTICS AND PROBLEM-SOLVING (Volume 2). This volume deals with details of heuristic approaches and the infinite aspects and features of ‘problem-solving’ and related issues. The author of the first article I quote suggests that the heuristic tools or devices he mentions will enable individuals to produce philosophy. He seems to think that this idea is one of the major factors that leads to the creation of philosophy. I wish to indicate, by citations, that there is much, much more to heuristics then the list of heuristics he suggests. I place the use of heuristic devices in the larger context of problem-solving. The solving of problems is of course merely one aspect of a much larger process that consist of many other features, steps and stages. The aim of that section and citations are to to make individuals aware of the many aspects of the process of problem conceptualization, investigation and solving or dissolving. I think it is is essential to be aware of these features of problem investigation because without such knowledge and understanding philosophers will suffer from an even greate lack of meta-cognition of the socio-cultural practice of philosophy and the doing of philosophy and of self-metacognition.
Suggested Citation: Suggested Citation
Ulrich De Balbian (Contact Author)
Meta-philosophy research center ( email ).
Ville Neuve Le Quiou, 226100 France
Meta-Philosophy Research Cente ( email )
Le Quiou Rennes, Bretagne 226100 France 0833833455 (Phone)
HOME PAGE: http://https://www.facebook.com/pg/Meta-Philosophy-Research-Center-721985114630696/about/
Do you have a job opening that you would like to promote on SSRN?
Paper statistics, related ejournals, cognition & culture: culture, communication, design, ethics, morality, religion, rhetoric, & semiotics ejournal.
Subscribe to this fee journal for more curated articles on this topic
Cultural Anthropology: History, Theory, Methods & Applications eJournal
Psychological anthropology ejournal, metaphilosophy ejournal.
Subscribe to this free journal for more curated articles on this topic
Linguistic Anthropology eJournal
Cognitive psychology ejournal.
Prepare for your exams
- Guidelines and tips
Study with the several resources on Docsity
Earn points by helping other students or get them with a premium plan
Prepare for your exams with the study notes shared by other students like you on Docsity
The best documents sold by students who completed their studies
Summarize your documents, ask them questions, convert them into quizzes and concept maps
Clear up your doubts by reading the answers to questions asked by your fellow students
Earn points to download
For each uploaded document
For each given answer (max 1 per day)
Choose a premium plan with all the points you need
Study Opportunities
Connect with the world's best universities and choose your course of study
Ask the community for help and clear up your study doubts
Discover the best universities in your country according to Docsity users
Free resources
Download our free guides on studying techniques, anxiety management strategies, and thesis advice from Docsity tutors
From our blog
summative test for intro to philosophy, Cheat Sheet of Philosophy
a summative test for the introduction of philosophy
Typology: Cheat Sheet
Limited-time offer
Uploaded on 09/05/2021
On special offer
Related documents
Partial preview of the text.
Lecture notes
Study notes
Document Store
Latest questions
Biology and Chemistry
Psychology and Sociology
United States of America (USA)
United Kingdom
Sell documents
Seller's Handbook
How does Docsity work
United States of America
Terms of Use
Cookie Policy
Cookie setup
Privacy Policy
Sitemap Resources
Sitemap Latest Documents
Sitemap Languages and Countries
Copyright © 2024 Ladybird Srl - Via Leonardo da Vinci 16, 10126, Torino, Italy - VAT 10816460017 - All rights reserved
| | | | | |
|
Cloud Chamber: Positron Trace | |
- Links for Introduction to Philosophical Inquiry
- Online Home
- Online Schedule
- Campus Home
- Campus Schedule
- Online Syllabus
- Sample Quizzes
- SampleTests
- On Campus FAQ
since 01.01.06
Characteristics of a Philosophical Problem
Abstract: A working definition of philosophy is proposed and a few philosophical problems are illustrated.
- philo —fond of, affinity for; e.g. , the name "Philip" means "lover of horses."
- sophia —wisdom; e.g. , the name "Sophie" means "wisdom."
- Almost any area of interest has philosophical aspects. For example, name an area and place the phrase “philosophy of” in front of it as in philosophy of science, philosophy of art, and philosophy of science. Or name the area and place the word “philosophy” after it as in political philosophy and ethical philosophy.
- Recently, philosophy of sport, medical ethics, and ethics of genetics have generated much interest.
- Some restaurants have printed on the back of the customer's bill their philosophy of restaurant management.
- In general, philosophy questions often are a series of "why-questions," whereas science is often said to ask "how-questions."
- E.g. , asking "Why did you come to class today?" is the beginning of a series of why-questions which ultimately lead to the answer of the principles or presuppositions by which you lead your life. I.e., Answer: "To pass the course." Question: "Why do you want to pass the course?" Answer: "To graduate from college." Question: "Why do you want to graduate?" Answer: "To get a good job." Question: "Why do you want a good job?" Answer: "To make lots of money." Question: "Why do you want to make money?" Answer: "To be happy." Hence, one comes to class in order to increase the chances for happiness.
| Characteristics | Typical Examples |
|---|---|
| 1. A reflection about the world and the things in it. | If I take a book off my hand, what's left on my hand? If I take away the air, then what's left? If I take away the space? With the space gone, nothing is left. Does everything in nothing? |
| 2. A conceptual rather than a practical activity. | According to Newton's gravitation theory, as the ballerina on a New York stage moves, my balance is imperceptibly affected. Since the earth's circumference is about 25,000 miles, and the earth spins around once every 24 hours, as I sit at my desk, I am in reality looping through space in giant arcs at over 25,000 miles per hour. |
| 3. The use of reason and argumentation to establish a point. | Does a tree falling in a forest with no one around to hear it, make a sound? To solve, we distinguish two senses of "sound": (1) hearing—a phenomenological perception and (2) vibration—a longitudinal wave in matter. So if no one is there to hear, there is no sound of type 1, but there is sound of type 2, as can be determined by the prior leaving a recording device on the scence. |
| 4. An explanation of the puzzling features of things. | Does a mirror reverse left and right? If I move my right hand, the image's left hand moves. But why then doesn't the mirror reverse up and down? Why aren't the feet in the mirror image at the top of the mirror? Why doesn't it change the situation if I lie down or I rotate the mirror 90 degrees? |
| 5. Digging beyond the obvious. | What is a fact? In science, facts are collected. Is a book a fact? Is it a big or little fact? Is the book a smaller fact than the earth which is a larger fact. If the book is brown, is that a brown fact? If facts don't have size, shape, and color, then in what manner do they exist in the world? And how can they be found? |
| 6. The search for principles which underlie phenomena. | Is a geranium one flower or is it a combination of many small flowers bunched together? If I turn on a computer, does one event occur or do many events occur? |
| 7. Theory building from these principles. | Is nature discrete or continuous? , Consider Zeno's paradoxes of motion. If you are to leave the classroom today, isn't it true that you will have to walk at least half-way to the door? And then when you get half-way, you will have to at least walk another half? How many "halves" are there? How will you ever get out? |
- Under the assumption that time is a dimension just like any other, the case of the problem of the surprise examination can arise: Suppose students obtain the promise from their teacher that a surprise quiz scheduled be given next week will not be given, if the students demonstrate how they can know, in advance, the day the teacher will give the exam. Thus, the students can argue as follows: Assuming the class meets only on Monday, Wednesday, and Friday, the students know the surprise exam cannot be given on Friday because everyone would know Thursday night that the following day is the only period left in which to give the exam. One would think that the teacher could give the exam Wednesday, but since Friday has been eliminated as a possibility, on Tuesday night, the students would know that the only period left in the week would be Wednesday (since Friday has already been eliminated; hence, the exam could not be given Wednesday either. Monday, then, is the only possible period left to offer the exam. But, of course, the teacher could not give the exam Monday because the students would expect the exam that day. Consequently, the teacher cannot give a surprise examination next week.
- Is a positron, or even the earlier tachyon, discussed above, associated with backward causation a possible event? Consider this paradoxical result. Suppose a "positron gun" or a "tachyon gun" would fire a particle going backward in time—it could "trigger" an off-switch to turn off the gun before it could be fired.
- This example is, of course, a thought-experiment. As Feynman noted in his Lectures on Physics , "Philosophers say a great deal about what is absolutely necessary for science, and it is always, so far as one can see, rather naive, and probably wrong.
- E.g. , for the problem of the sound of a tree falling in a forest with no one around to hear, all we need do is distinguish two different senses of "sound."
- If by "sound" is meant a "phenomenological perception by a subject," then no sound ("hearing") would occur. If by "sound" is meant "a longitudinal wave in matter," then a sound is discoverable.
- Calling — if a person has had experiences of curiosity, discovery, and invention at an early age, these experiences could leave an imprint on mind and character to last a lifetime.
- Ask a Philosopher Archive. Submitted philosophical questions are answered in some detail by philosophers, a project maintained by the International Society for Philosophers. You may submit your questions on the Ask a Philosopher page.
- Backward Causation. Jan Fey's entry in the Stanford Encyclopedia of Philosophy examines several paradoxes based on the notion where an effect temporally, but not causally, precedes its cause.
- Paradox. An extensive reference list of paradoxes in Wikipedia is summarized by topic in mathematics, logic, practice, philosophy, psychology, physics and economics with links to more extensive discussion.
- Unexpected Hanging Paradox. Eric W. Weisstein at the site Wolfram MathWorld provides another version of the Surprise Examination Paradox with a list of further references.
“203. Language is a labyrinth of paths. You approach from one side and know your way about; you approach the same place from another side and no longer know your way about.” Ludwig Wittgenstein, Philosophical Investigations Trans. G. E. M. Anscombe, 3rd. ed. (New York: The Macmillan Company), 1958), 82 e .
Relay corrections, suggestions or questions to larchie at lander.edu Please see the disclaimer concerning this page. This page last updated 01/27/24 © 2005 Licensed under the GFDL
Last updated 27/06/24: Online ordering is currently unavailable due to technical issues. We apologise for any delays responding to customers while we resolve this. For further updates please visit our website: https://www.cambridge.org/news-and-insights/technical-incident
We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings .
Login Alert

- > Journals
- > Volume 4 Issue 12
- > What is a philosophical problem?

Article contents
What is a philosophical problem.
Published online by Cambridge University Press: 22 July 2009
To what extent are philosophical questions and problems like other kinds of questions and problems, such as the those tackled by the physical sciences? Peter Hacker suggests that the problems of philosophy are conceptual, not factual, and that their solution or resolution is more a contribution to a particular form of understanding than to our knowledge of the world.
Access options

This article has been cited by the following publications. This list is generated based on data provided by Crossref .
- Google Scholar
View all Google Scholar citations for this article.
Save article to Kindle
To save this article to your Kindle, first ensure [email protected] is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about saving to your Kindle .
Note you can select to save to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be saved to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.
Find out more about the Kindle Personal Document Service.
- Volume 4, Issue 12
- P.M.S. Hacker
- DOI: https://doi.org/10.1017/S1477175600001664
Save article to Dropbox
To save this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Dropbox account. Find out more about saving content to Dropbox .
Save article to Google Drive
To save this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you used this feature, you will be asked to authorise Cambridge Core to connect with your Google Drive account. Find out more about saving content to Google Drive .
Reply to: Submit a response
- No HTML tags allowed - Web page URLs will display as text only - Lines and paragraphs break automatically - Attachments, images or tables are not permitted
Your details
Your email address will be used in order to notify you when your comment has been reviewed by the moderator and in case the author(s) of the article or the moderator need to contact you directly.
You have entered the maximum number of contributors
Conflicting interests.
Please list any fees and grants from, employment by, consultancy for, shared ownership in or any close relationship with, at any time over the preceding 36 months, any organisation whose interests may be affected by the publication of the response. Please also list any non-financial associations or interests (personal, professional, political, institutional, religious or other) that a reasonable reader would want to know about in relation to the submitted work. This pertains to all the authors of the piece, their spouses or partners.
We've detected unusual activity from your computer network
To continue, please click the box below to let us know you're not a robot.
Why did this happen?
Please make sure your browser supports JavaScript and cookies and that you are not blocking them from loading. For more information you can review our Terms of Service and Cookie Policy .
For inquiries related to this message please contact our support team and provide the reference ID below.

COMMENTS
The problem was originally formulated in 1965 by Edsger Dijkstra, and is stated as follows: X amount of philosophers sit at a round table with bowls of food. Forks are placed in front of each ...
Illustration of the dining philosophers problem. Each philosopher has a bowl of spaghetti and can reach two of the forks. In computer science, the dining philosophers problem is an example problem often used in concurrent algorithm design to illustrate synchronization issues and techniques for resolving them.. It was originally formulated in 1965 by Edsger Dijkstra as a student exam exercise ...
Take the right fork. Take the left fork. Eat food. Put the left fork back. Put the right fork back. Repeat the whole process again, i.e. go to step 1. If a philosopher wants to take a fork, but this fork is currently used by the neighbor, the philosopher waits until the neighbor puts the fork back before getting it.
Meals are taken communally in a table with five plates and five forks in a cyclic manner as shown in the figure. Constraints and Condition for the problem : Every Philosopher needs two forks in order to eat. Every Philosopher may pick up the forks on the left or right but only one fork at once. Philosophers only eat when they had two forks.
A third possibility for solving the dining philosophers problem is to impose a linear ordering on the semaphores. This order could be imposed by requiring i < j anytime sems[i] is accessed before sems[j]. As before, thread 0 would wait on semaphores 0 and 1 (in that order), thread 1 would wait on semaphores 1 and 2, and so on.
Algorithms. 1. Overview. In this tutorial, we'll discuss one of the famous problems in concurrent programming - the dining philosophers - formulated by Edgar Dijkstra in 1965. He presented the problem as a demonstration of the problem of resource contention. It occurs when computers need to access shared resources. 2.
The Solution of the Dining Philosophers Problem. The solution to the process synchronization problem is Semaphores, A semaphore is an integer used in solving critical sections. The critical section is a segment of the program that allows you to access the shared variables or resources.
6.4: Dining Philosopher Problem. In computer science, the dining philosophers problem is an example problem often used in concurrent algorithm design to illustrate synchronization issues and techniques for resolving them. It was originally formulated in 1965 by Edsger Dijkstra as a student exam exercise, presented in terms of computers ...
The dining philosophers problem is a famous problem in computer science used to illustrate common issues in concurrent programming. The problem was originally formulated in 1965 by Edsger Dijkstra…
The Dining Philosophers Problem serves as an abstract representation of real-world challenges like highlighting the need for synchronization techniques to ensure the fair allocation of resources and prevent deadlock. To solve this critical section problem, we use an integer value called semaphore. Approach to Solution. Here is the simple ...
The dining philosopher's problem is the classical problem of synchronization which says that Five philosophers are sitting around a circular table and their job is to think and eat alternatively. A bowl of noodles is placed at the center of the table along with five chopsticks for each of the philosophers. To eat a philosopher needs both their ...
The steps for the Dining Philosopher Problem solution using semaphores are as follows. 1. Initialize the semaphores for each fork to 1 (indicating that they are available). 2. Initialize a binary semaphore (mutex) to 1 to ensure that only one philosopher can attempt to pick up a fork at a time. 3.
Philosophers employ a skeptical attitude in looking at ideas, events, or things. Systematic doubt. ... It is a problem-solving device used in analyzing possible explanations regarding a phenomenon. Occam's razor. This principles states that among possible explanations, the one which has the least assumptions is the most acceptable. ...
it is a problem-solving device used in analyzing possible explanations regardingba phenomenom. Formal Logic it is a systematic analysis of the validity of arguments and statements.
Definition Let's start off easy. A "Philosophical Problem" is like a super tough riddle about life and the universe that even the smartest people can't quite solve. Imagine you've found a strange puzzle box at a garage sale with no instructions. Opening it is tough because you don't know how it works, yet you have a feeling that you can figure it out. That's what a philosophical ...
Plato believed doing the right thing would lead to excellence and success. This concept echoes today, emphasizing personal growth, achievement, and the value of ethical actions. Perseverance. Plato encouraged continual progress, even if slow, implying the value of persistence. The value of perseverance remains critically appreciated in modern ...
Dining-Philosophers Problem - N philosophers seated around a circular table. There is one chopstick between each philosopher. A philosopher must pick up its two nearest chopsticks in order to eat. A philosopher must pick up first one chopstick, then the second one, not both at once. We need an algorithm for allocating these limited resources ...
theoretical analyses of problem-solving methods, and often suggest strategies or heuristics for better problem-solving techniques.1 One might say they are dealing with the "logic" of problem solving. At the same time, philosophers of science - who often double as historians of science - are partly interested in problem solving as a descriptive tool
This volume deals with details of heuristic approaches and the infinite aspects and features of 'problem-solving' and related issues. The author of the first article I quote suggests that the heuristic tools or devices he mentions will enable individuals to produce philosophy. He seems to think that this idea is one of the ...
Certainty d. Ethics 9. It as a body of knowledge provides methodologies and insights on how societal questions, can be answered a. Epistemology c. Metaphysics b. Philosophy d. Ethics 10. One of the methods or problem solving device used by the philosophers which are the imagined scenarios used to illustrate a certain problem or describe a ...
Problem statement. Five silent philosophers sit at a round table with bowls of spaghetti. Forks are placed between each pair of adjacent philosophers. Each philosopher must alternately think and eat. However, a philosopher can only eat spaghetti when they have both left and right forks. Each fork can be held by only one philosopher and so a ...
Answer: "To be happy." Hence, one comes to class in order to increase the chances for happiness. As I remember Avrum Stroll and Richard H. Popkin, in their highly readable book, Introduction to Philosophy, isolate seven characteristics of a philosophical problem. These characteristics serve as a good introduction to mark some of the perplexing ...
Peter Hacker suggests that the problems of philosophy are conceptual, not factual, and that their solution or resolution is more a contribution to a particular form of understanding than to our knowledge of the world. Type. Research Article. Information. Think , Volume 4 , Issue 12 , Spring 2006 , pp. 17 - 28.
Connecting decision makers to a dynamic network of information, people and ideas, Bloomberg quickly and accurately delivers business and financial information, news and insight around the world